Construction

1) Départ

Le point de départ est un triangle ABC, et la donnée de trois points P, Q, R du plan (pas tout le plan tout de même) dont dépend la suite de la construction. Le cercle circonscrit à ABC jouera aussi un rôle dans cette aventure :

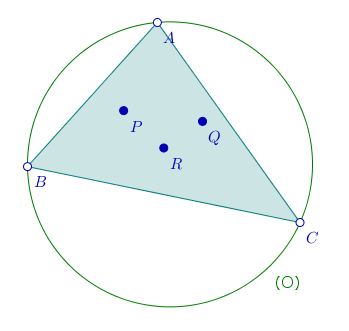
2) Le point P

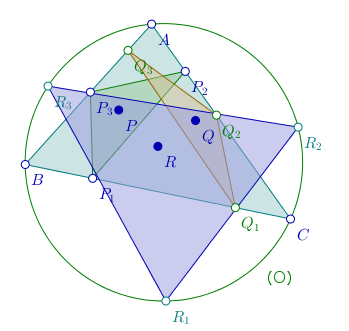
La droite AP (qui répond au doux nom de cévienne issue de A) coupe le côté opposé en P1. De façon analogue on définit P2 et P3 (les « pieds des céviennes »). Les trois points ainsi construits forment un triangle dépendant de P (son « triangle cévien ») :

3) Le point Q

On fait pareil pour le point Q, ce qui définit un nouveau triangle cévien dont les sommets sont, dans l’ordre, Q1, Q2 et Q3 :

4) Le point R

Légère variante : On ne considère plus les intersections de (AR), (BR) et (CR) avec le triangle mais avec le cercle circonscrit :

5) Le point S1

Le cercle circonscrit au triangle P1Q1R1 coupe le cercle circonscrit à ABC en deux points ; l’un d’eux est R1, l’autre est un point nouvellement construit (avec l’option « loin de » de CaRMetal), appelé S1 :

6) Les points S2 et S3

On construit de même les points S2 et S3 :

7) L’énoncé du théorème

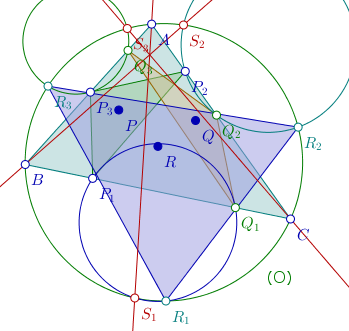
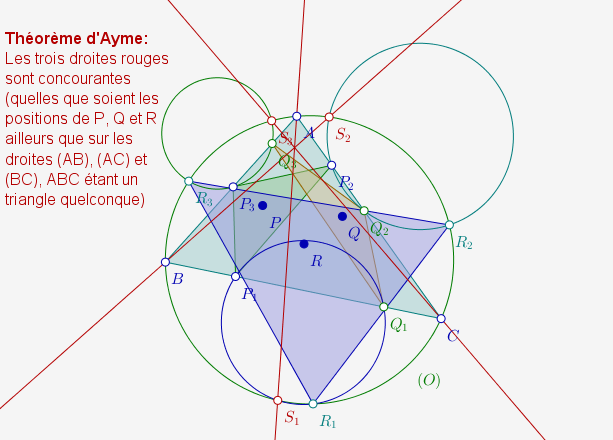
Les trois droites (AS1), (BS2) et (CS3) passent par un même point.

Les doites sont représentées en rouge ci-dessous :

Figure

Manipuler les sommets du triangle ou les trois points P, Q et R permet de se convaincre de la concourance des trois droites :

TP

La construction à elle seule peut être un exercice qui

1. familiarise les élèves avec le logiciel de géométrie dynamique
2. familiarise les élèves avec la démarche algorithmique [1]
3. permet une pédagogie différenciée (les élèves les plus rapides pouvant explorer les cas particuliers de céviennes)
4. permet de signaler qu’un théorème sur le triangle dont l’énoncé est presque élémentaire, peut encore être découvert au XIX^e siècle.

Voici l’énoncé du TP :

• Plusieurs élèves ont eu du mal avec le début de la construction, parce qu’ils ont coupé avec la droite (AP), non pas la droite (BC) mais le côté [BC] du triangle. L’effet de cette erreur est le même avec GeoGebra qu’avec CaRMetal : La figure ne résiste pas à un mouvement excessif du point P. Toutefois la correction est plus facile avec GeoGebra qu’avec CaRMetal, il suffit de redéfinir le point d’intersection en remplaçant le nom du segment par celui de la droite.
• Certains élèves trouvent logique d’utiliser la gomme pour détruire des objets (cas de GeoGebra), d’autres trouvent logique de l’utiliser pour cacher un objet (cas de CaRMetal). Concrètement, pour eux, la différence entre les deux comportements se voit surtout lorsqu’on gomme un objet dont d’autres dépendent : Ceux-ci disparaissent avec GeoGebra, pas avec CaRMetal. Mais cette différence n’est pas vraiment perçue par les élèves, dont certains font un dessin plus qu’une figure.
• La figure n’est vraiment correcte à la fin, que si le point Sa est « loin de » Ra ; sinon il peut coller à Ra avec certains mouvements de la souris, et la concourance n’est plus assurée. Alors qu’avec CaRMetal, il suffit de cliquer sur « loin de » puis sur le point Ra, la manipulation analogue est plus compliquée sous GeoGebra (créer deux points auxiliaires avec l’outil intersection, puis un point dont les coordonnées sont égales à l’un des deux selon des variables booléennes). De toute manière aucun élève n’a eu le temps de faire la construction en moins d’une heure avec GeoGebra, la construction semblant nettement plus rapide à faire avec CaRMetal, au moins pour ceux qui ont bien utilisé des droites dès le début).

Certaines des figures du TP sont visibles ici.