arboriculture
On sait qu’une expression algébrique est en fait, un arbre. Donc les opérations algébriques comme le développement ou la factorisation d’expressions s’illustrent par des modifications de l’arbre : De l’arboriculture !
Puisqu’une expression est un arbre, qu’est-ce qu’une équation alors ? Et bien, un arbre aussi, dont le nœud est une égalité, et binaire au départ, puisque l’équation a deux membres (des expressions) eux-mêmes représentés par des sous-arbres. Par exemple, l’équation $2x+1=x-2$ est représentée par cet arbre (les opérations en rouge, les nombres en bleu) :
Ce qui est confirmé par l’examen de cette équation dans l’inspecteur DOM de Firefox (sous ekoarun) :
Alors les opérations algébriques de factorisation, développement et résolution d’équation, s’illustrent graphiquement par des transformations d’arbres, avec des régles comme
- Si un nœud porte une opération commutative (+, * ou = ) on peut échanger les deux sous-arbres qui en partent ;
- Si un nœud porte une opération anti-commutative, on peut se ramener au cas précédent en écrivant une différence comme somme avec l’opposé, et un quotient comme produit par l’inverse.
- Si on passe un terme d’un membre à l’autre, on échange les additions avec les soustractions ;
- Si on passe un facteur d’un membre à l’autre , on transforme la multiplication en division, et on modifie le sens de l’inégalité si le facteur est négatif...
C’est ce que permet ekoarun en transformant l’équation ci-dessus par passage du 1 à droite, l’abre devient alors
Là encore, la vue en 3D de l’inspecteur DOM de Firefox montre le nouvel arbre :
Les règles d’algèbre, illustrées sur l’arbre, ont déjà été explorées ici et sont appelées algèbre dynamique par Jean-François Nicaud qui en a même fait la théorie.
Voici, pour s’entraîner à l’utilisation d’ekoarun, quelques tutoriels de niveau collège ; on peut les suivre en utilisant la version d’ekoarun qui est en ligne ci-dessous.
Addition des relatifs
Pour commencer, voici un exercice du manuel « Mathenpoche 5e » de Sesamath (page 56 n° 42 b ; additions de relatifs à effectuer) :
| b. (-9) + (-14) + (+25) + (-3) |
Remarque : ekoarun est un logiciel d’équations. Pas une calculatrice. Le présent exemple détourne donc ekoarun de sa fonction initiale, qui est de résoudre des équations. Pour ce faire, on doit donc faire croire à ekoarun qu’on est en train de résoudre une équation, et pas seulement de faire un calcul. L’astuce est simple, il suffit d’insérer x= devant le calcul à effectuer.
Première méthode
- Cliquer successivement sur x, =, -, 9, +, -, 1, 4, +, 2, 5, +, -, 3 puis « insérer ».
- Glisser le -9 sur le -14.
- Glisser le -23 obtenu sur le 25.
- Glisser enfin le 2 sur le 3.
Seconde méthode [2]
- Cliquer successivement sur x, =, -, 9, -, 1, 4, +, 2, 5, -, 3 puis « insérer ».
- Sélectionner -9 et -14 (en cliquant dessus) puis cliquer sur « Σ » pour effectuer la première addition.
- Sélectionner -23 et 25 puis cliquer sur Σ à nouveau.
- Terminer comme précédemment.
Sommes de fractions
Pour additionner 1/4 avec 1/2, on fait comme avec les sommes algébriques, en affectant une variable x par 1/4+1/2 :
- Après avoir éventuellement effacé, cliquer sur x, =, 1, /, 4, +, 1, /, 2 puis « insérer » ;
- Faire glisser la première fraction vers la deuxième : La somme s’écrit alors $x=\frac{6}{8}$ ;
- Pour simplifier la fraction obtenue, la sélectionner puis cliquer sur le premier bouton qui apparaît alors (et qui indique d’ailleurs la forme irréductible).
Voici le début du sujet de brevet centres étrangers 2012 :
| Calculer $\frac{1}{4}+\frac{2}{3}\times \frac{3}{4}$ |
Là c’est plus difficile pour ekoarun, puisque celui-ci n’a pas de signe de multiplication [3]. Alors il faut considérer la fraction 2/3 comme un coefficient et la fraction 3/4 par laquelle elle sera multipliée, comme une variable x :
- Effacer, puis cliquer successivment sur x, =, 3, /, 4 et « insérer » pour avoir l’équation $x=\frac{3}{4}$ ;
- sélectionner x puis cliquer sur © pour le copier ;
- Effacer, puis cliquer sur y, =, 1, /, 4, +, 2, /, 3, x et « insérer », pour avoir l’équation $y=\frac{1}{4}+\frac{2}{3}x$ ;
- Injecter x dans cette nouvelle équation en cliquant sur la flèche « ↪ » ;
- Simplifier la somme obtenue, soit en simplifiant d’abord 6/12 puis en additionnant à 1/4, soit en additionnant d’abord les deux fractions puis en simplifiant la somme, soit en cliquant sur « all » puis sur « Σ » et « 1/2 » pour simplifier...
Sommes de fonctions affines
Extrait de Sesamath 5e (page 70 n° 30) :
| Regroupe puis réduis les expressions : A = 16x + 7 - 9x +2 |
Pour faire cet exercice, on va remplacer A par y, celui-ci figurant (contrairement à A) dans le clavier d’ekoarun :
- Après avoir éventuellement effacé, cliquer successivement sur y, =, 1, 6, x, +, 7, -, 9, x, +, 2 et « insérer » ;
- glisser le 7 sur le 2 ;
- glisser le 16x sur le 9x ;
- fini !
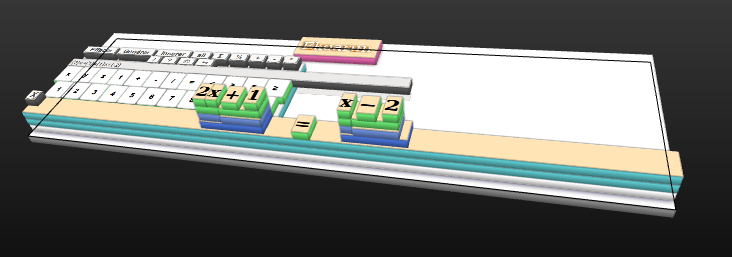
Résolution d’une équation
Exercice 3 du sujet du brevet Asie 2012 :
| On considère la fonction f définie par : f(x) = −5x + 1 1. Calculer l’image de −3 par f . 2. Calculer l’antécédent de 4 par f . |
Comme ekoarun n’a pas de lettre f dans son clavier, on va utiliser y à la place de f(x) :
- Pour l’image de -3, on va créer une équation auxiliaire qui est juste x=-3 :
- Cliquer sur x, =, -, 3 puis « insérer ».
- puis cliquer sur © pour mettre -3 dans la mémoire x [4].
- Créer ensuite l’équation y=-5x+1 en cliquant successivement sur y, =, 5, x, +, 1 et « insérer ».
- Cliquer sur la flèche « ↪ » pour remplacer x par -3, puis glisser le 1 sur le 15 pour avoir la réponse.
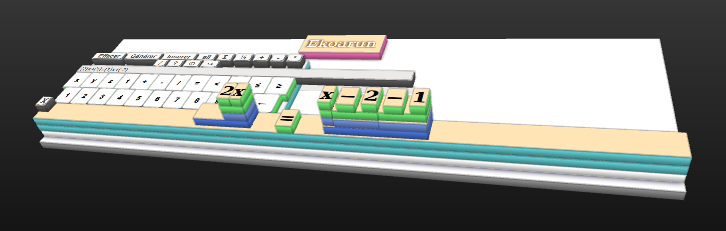
- Pour chercher l’antécédent de 4, on résout l’équation 4=-5x+1.
- Cliquer successivement sur 4, =, 5, x, +, 1 et « insérer » pour créer l’équation.
- Faire glisser le terme 5x jusqu’au membre de gauche pour transformer l’équation en -5x+4=1 [5] ;
- Faire glisser le 4 vers le membre de droite pour transformer l’équation en -5x = 1-4.
- Faire glisser le 1 sur le 4 pour simplifier le second membre [6] ;
- On ne peut pas faire passer le -5 dans le membre de droite parce que -5 n’est pas un terme mais un facteur. Alors sélectionner tout le terme -5x puis choisir la multiplication par l’inverse de -5 ;
- sélectionner le facteur devant x et le simplifier en cliquant sur le premier bouton du menu contextuel pour transformer le premier membre en x ;
- de même sélectionner le second membre puis choisir la simplification pour avoir le second membre sous forme irréductible [7] ; l’équation est résolue.
- On peut faire comme en Seconde et afficher l’ensemble des solutions en cliquant sur « ? »
Résolution d’une inéquation
Extrait du sujet du brevet des collèges Nouvelle-Calédonie mars 2011 :
| Certains fournisseurs proposent de l’électricité « bio ». Une famille étudie deux tarifs d’électricité « bio » qui lui sont proposés. On note x le nombre de Kwh d’électricité « bio » consommé. On note T1(x) le coût de l’électricité consommée en un mois pour le tarif 1. On note T2(x) le coût de l’électricité consommée en un mois pour le tarif 2. On admet que T1(x) = 24x et que T2(x) = 3600 + 14x. Trouver en fonction de sa consommation, le tarif le plus avantageux pour cette famille. |
Il s’agit, en bref, de résoudre l’inéquation 24x≤3600+14x. Voici la démarche à effectuer :
Cliquer successivement sur 2, 4, x, ≤, 3, 6, 0, 0, +, 1, 4, x puis « insérer ».
Faire passer le terme 14x vers la gauche, en deux étapes : D’abord dans le premier membre, puis sur le terme 24x. On obtient alors 10x≤3600.
Sélectionner 10x, puis choisir la division (par 10). Cliquer sur « all » puis sur « 1/2 ». L’inéquation est résolue au niveau collège puisqu’on a x≤360. Pour la résoudre au niveau lycée (avoir l’ensemble des solutions), cliquer sur le bouton « ? » qui rajoute l’affichage S = ]-∞ ; +360].
Pour multiplier à l’envi les exercices de résolution d’équation ou d’inéquation, cliquer sur « générer » puis sur « insérer ».
Résolution d’un système
Ci-dessous on va voir comment ekoarun peut être utilisé pour résoudre cet exercice du brevet des collèges Amérique du Nord 2013 :
| Arthur vide sa tirelire et constate qu’il possède 21 billets. Il a des billets de 5 € et des billets de 10 € pour une somme totale de 125 €. Combien de billets de chaque sorte possède-t-il ? |
Le système à résoudre est donc formé des deux équations
- x+y = 21
- 5x+10y=125
x et y désignant le nombre de billets de 5 € et le nombre de billets de 10 € respectivement.
Pour entrer la première équation, cliquer successivement sur les boutons x, +, y, =, 2, 1, puis sur « insérer ». Puis attraper le x du premier membre pour le faire glisser vers le second membre : L’équation s’est alors transformée en y=21-x ou y=-x+21.
Important : C’est maintenant qu’il faut sélectionner le premier membre y, puis le copier (en vue d’un coller ultérieur) avec ©. En effet, le membre mis en mémoire à ce moment est extrait de la dernière équation entrée, et cette manipulation ne sera plus possible une fois qu’on aura créé la seconde équation.
Cliquer sur « effacer » pour commencer à entrer la seconde équation, en cliquant successivement sur 5, x, +, 1, 0, y, =, 1, 2, 5 et à nouveau sur « insérer ».
Cliquer sur le bouton d’injection « ↪ », qui va transformer la seconde équation en 5x+210-10x=125. Résoudre cette équation avec les méthodes vues ci-dessus, jusqu’à obtenir x=17.
Copier ensuite cette valeur de x (17) en cliquant sur © après avoir sélectionné x. Mais si on essaye d’injecter 17 à la place de x, l’injection se fera dans l’équation x=17 et donnera 17=17, ce qui n’est pas ce qu’on veut.
Créer alors une troisième équation, en effaçant puis en cliquant successivement sur y, =, 2, 1, -, x (pour reproduire la première équation y=21-x et qu’elle soit à la fin) ; puis injecter (avec « ↪ »), ce qui devrait donner y=21-17 qu’on peut résoudre en faisant glisser le 21 sur le 17...
Voici le logiciel en ligne, pour s’exercer :
Pour ouvrir ekoarun dans un autre onglet du navigateur : cliquer ici !
Des tutoriels vidéo sont sur cette chaîne
Commentaires