Si C1 et C2 se coupent en A et B, d’après la remarque ci-dessus, tous les cercles du faisceau passent par A et B : On dit que A et B sont les points de base du faisceau, lequel est formé des cercles passant par A et B :

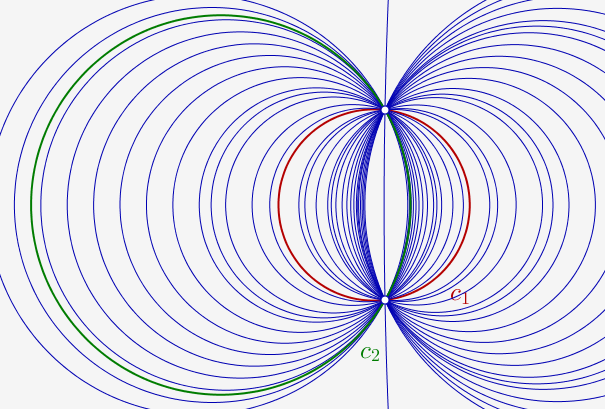
L’un des cercles est très grand, il suggère que la droite (AB) est elle-même membre du faisceau de cercles, comme cas limite.

Si C1 et C2 sont tangents en A, tous les cercles du faisceau passent par A, et sont tangents entre eux en A :

La tangente commune à tous les cercles fait aussi partie du faisceau, comme cercle de rayon infini.

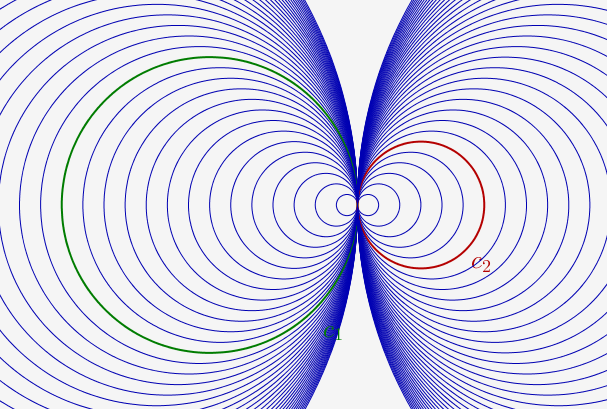
Si C1 et C2 n’ont aucun point commun, le faisceau qu’ils engendrent est dit de Poncelet, et il contient deux cercles de rayon nul, appelés points limites ou points de Poncelet du faisceau.

On devine une droite dans le faisceau : Elle est verticale, entre C1 et C2 (et entre les deux points limite)

On suppose que C1 et C2 ne sont pas tous les deux des droites ; alors

On appelle axe radical de C1 et C2, la seule droite qui fait partie du faisceau engendré par C1 et C2.

En déplaçant les deux cercles et en observant la position de leur axe radical, on observe expérimentalement les faits suivants :

• Si les deux cercles sont sécants en S et T, leur axe radical est la droite (ST) ;
• S’ils sont tangents en T, leur axe radical est leur tangente commune en T ;
• S’ils sont extérieurs l’un à l’autre, les points S et T sont devenus invisibles parce qu’ils sont imaginaires conjugués ; mais leur milieu est toujours réel, et l’axe radical de C1 et C2 passe par ce milieu ; l’axe radical est alors entre C1 et C2.
• Si le plus petit cercle est à l’intérieur de l’autre, l’axe radical est à l’extérieur des deux cercles. Sa position dépend de celle des cercles, de manière assez sensible ;
• Cas limite : Si les deux cercles sont concentriques, leur axe radical est à l’infini.
• Dans tous les autres cas, l’axe radical est perpendiculaire à la droite joignant les centres des deux cercles.

On considère un cercle (supposé dans un faisceau à points de Poncelet) et un point (un des points de Poncelet). Alors l’axe radical du faisceau (en rouge) est défini comme fonction du point C et du cercle :

Cette droite, qui ne dépend que de C et du cercle (bleu), peut être appelée axe radical du point et du cercle. Par la suite, on considère l’image (en vert ci-dessus) de cette droite (rouge) par l’homothétie de centre C et de rapport 2.
Cette nouvelle droite dépend, elle aussi, de C et du cercle. On l’appelle polaire de C par rapport au cercle.

Si on mène par C une tangente au cercle, la polaire de C par rapport au cercle passe par le point de contact ce qui donne

• une utilité géométrique à la polaire d’un point
• un moyen de construire la polaire.

Cependant, si C est à l’intérieur du cercle, la polaire continue d’exister alors que le faisceau n’est plus à points de Poncelet. La polaire est une notion assez générale (existe ausi avec les coniques, y compris les coniques dégénérées).

En faisant glisser C le long d’une droite, on constate que sa polaire tourne autour d’un point P (en bleu) :

Ce point s’appelle le pôle de la droite rouge par rapport au cercle. Or

• P est sur la polaire de Q si, et seulement si, Q est sur la polaire de P
• P est le pôle de d si, et seulement si, d est la polaire de P.

Ceci permet de donner à l’ensemble des droites du plan projectif, une structure de plan projectif, où des droites sont dites proches si leurs pôles le sont.
Cette dualité permet d’associer à une courbe vue comme enveloppe de ses tangentes, une autre courbe qui est le lieu des pôles des tangentes.
Cette notion de enveloppe d’une famille de droites est intéressante pour modéliser la vision périphérique.

La droite (en jaune) joignant un point C au centre du cercle, est perpendiculaire à la polaire (en vert) de C par rapport au cercle :

Si les droites sont perpendiculaires, elles sont a fortiori sécantes.

Leur intersection C’ est appelée inverse de C par rapport au cercle.

L’inversion par rapport à un cercle est une involution (bijection égale à son inverse). Autrement dit, il revient au même de dire

• C’ est l’inverse de C par rapport au cercle
• C est l’inverse de C’ par rapport au cercle.

Dans les deux cas, on dit que C et C’ sont inverses l’un de l’autre.

Un point est son propre inverse si, et seulement si, il est sur le cercle.

Si on fait glisser le point C le long d’une droite (en rouge), on constate que son inverse parcourt un cercle (en vert) :

Ceci constitue une théorie de l’anamorphose : si on trace un cercle sur une feuille de papier, et qu’on pose un miroir cyclindrique sur la feuille, de telle manière que le centre du cercle soit sur le cylindre, le reflet du cercle est une droite.

Si, maintenant, le point C parcourt un cercle, son inverse C’ par rapport au cercle bleu, parcourt aussi un cercle (en vert) :

Si un cercle C’ est invariant par inversion par rapport au cercle C, on dit que C’ est orthogonal à C. Dans ce cas, le cercle C est également invariant par inversion par rapport à C’ et on dit que C et C’ sont orthogonaux (l’un par rapport à l’autre).

L’ensemble des cercles orthogonaux à tous les cercles d’un faisceau est lui-même un faisceau de cercles. Par exemple :

• les cercles qui sont orthogonaux à tous les cercles passant par A et B, forment un faisceau à points de Poncelet (A et B),
• inversement, les cercles orthogonaux à au moins deux cercles d’un faisceau à points de Poncelet, forment un faisceau à points de base : tous les cercles de ce faisceau passent par les deux points de Poncelet.
• Les cercles orthogonaux à un faisceau de cercles tangents, forment également un faisceau à cercles tangents. Le point de contact est le même mais les tangentes sont perpendiculaires entre elles.

Plus généralement, l’axe radical d’un faisceau de cercles est orthogonal à l’axe radical de son faisceau orthogonal.

Si les équipotentielles d’un champ scalaire forment un faisceau de cercles, alors les lignes de champ de son gradient forment un faisceau de cercles aussi : son faisceau orthogonal.