L’énoncé du TP est téléchargeable ici :
En fait aucun élève n’a réussi la première partie du TP (aussi celle-ci n’était-elle pas notée).
L’effet attendu était la création spontanée de l’algorithme suivant :
Mettre 3 dans x
Mettre 8 dans y
Mettre x dans y
Mettre y dans xC’est bien ce qui s’est passé. Mais les élèves n’ont pas pensé à créer une autre variable que x et y, pour y stocker temporairement les anciennes valeurs afin que celles-ci ne soient pas écrasées par les nouvelles. En effet, si on examine le script en mode pas-à-pas, on constate que le problème vient de la ligne 7, où y écrase x :
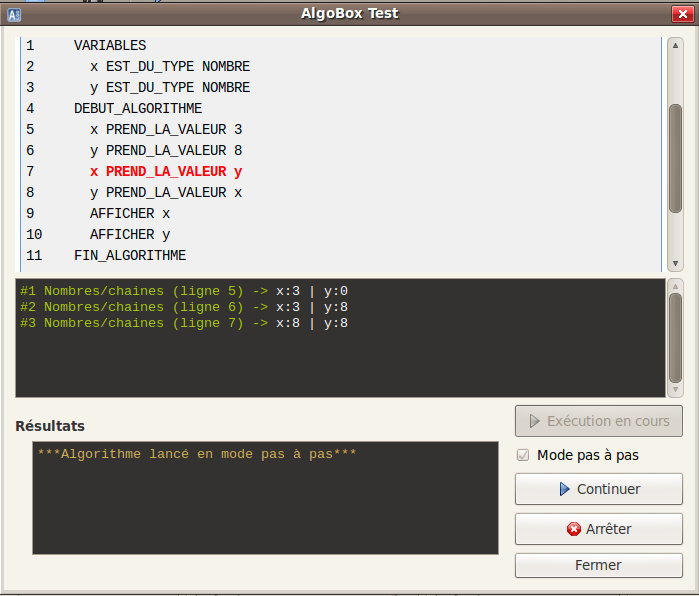
Surprenamment, ce phénomène semble très difficile à imaginer par les élèves : Alors que
x prend 3
x prend 8leur semble simple à comprendre (ils savent qu’à la fin, x=8), dans le cas présent, l’idée qu’on prenne le nombre dans y pour le mettre dans x leur paraît un mouvement (remplacement) et non une copie. L’image des nombres dans les tiroirs n’est donc pas idéale pour décrire un algorithme (quand on transfère le contenu d’un tiroir à un autre tiroir, le premier tiroir est vide !). Dans le cas présent, il s’agit plus d’une copie que d’un transfert. La description des tiroirs a alors été abandonnée pour parler de téléchargement :
Lorsque vous téléchargez un logiciel sur 01net, l’original qui se trouve sur le site 01net est-il modifié ? Disparaît-il ?
Réponse de certains élèves : « Je ne télécharge rien, de peur que ce ne soit pas libre » (humour de lycéen...)
La description de la situation par le remplissage progressif d’un tableau permet de mieux préciser ce qui se passe :
- Après la ligne 2, on a
| x | |
- Après la ligne 3, on a
| x | |
| y | |
- Après la ligne 5, on a
| x | 3 |
| y | |
- Après la ligne 6, on a
| x | 3 |
| y | 8 |
Mais après la ligne 7, on a
| x | 8 |
| y | 8 |
Le 3 ayant disparu dans les limbes, on ne peut plus le récupérer !
Le même tableau a facilité le corrigé : Pour peu que l’on pense à créer une troisième variable z, on a
| x | 3 |
| y | 8 |
| z |
puis, après avoir mis x dans z :
| x | 3 |
| y | 8 |
| z | 3 |
ce qui permet d’écraser une des occurences du 3 sans perdre ce nombre à tout jamais. La suite de l’algorithme donne successivement
| x | 8 |
| y | 8 |
| z | 3 |
puis par « transfert » (en fait, copie) de z vers y :
| x | 8 |
| y | 3 |
| z | 3 |
ce qui répond à la question.
Aucun élève n’a réussi à trouver cet algorithme, sauf un, qui avait utilisé deux variables (en JavaScript, un problème technique ayant fait renoncer à AlgoBox) :
var x=3;
var y=8;
var a=y;
var b=x;
x=a;
y=b;
Println(x);
Println(y);Seulement, à force de tâtonner dans tous les sens, cet élève a oublié le script ci-dessus, et a recréé de mémoire la version incomplète ci-dessous :

Les autres élèves ont opté pour des tentatives plus compliquées, parce que reposant sur des opérations et non des simples copies. Exemple typique :

La deuxième partie du TP, la seule qui était notée, était de la programmation : Traduire en JavaScript (pour la raison technique évoquée ci-dessus) l’algorithme de l’énoncé, puis le tester. L’erreur la plus fréquente a été l’oubli du signe de multiplication :

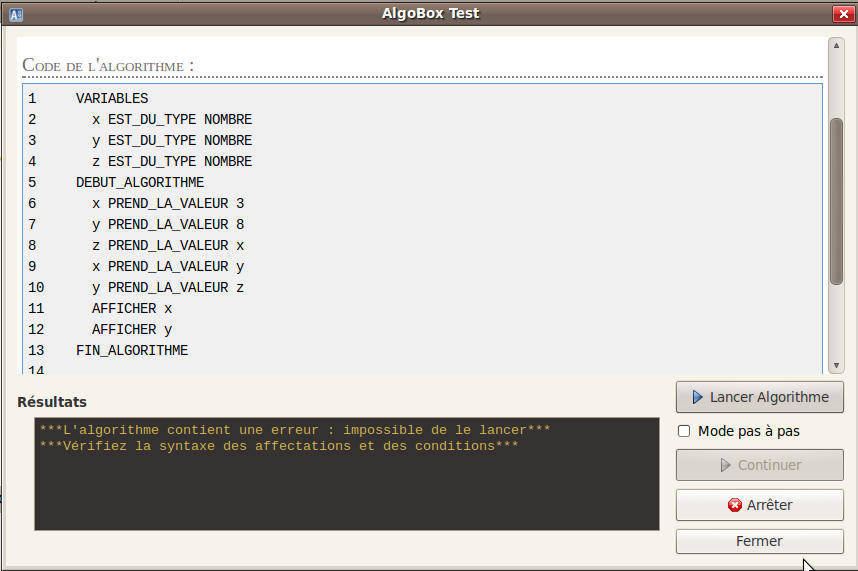
On remarquera à cet effet la richesse de l’affichage des erreurs de syntaxe par Rhino (moteur JavaScript), qui, s’il n’indique pas exactement la cause de l’erreur [1], met en exergue la ligne où est apparue l’erreur. Par contraste, qui se sentirait capable en moins de 10 minutes, de dire où est l’erreur dans le script AlgoBox ci-dessous ?
Or, 10 minutes quand on est dans une salle exigüe pleine d’ordinateurs surchauffés et d’élèves encore plus surchauffés (et trop nombreux) c’est énorme, surtout quand d’autres élèves appellent au secours au même moment...
La morale de ce TP, c’est que le choix de l’outil n’est nullement anodin : Avec leur affectation « simultanée » de plusieurs variables [2], les langages lua et Python rendent tout le TP inutile, comme le montre la séance IDLE ci-dessous :


Commentaires