Principe du tournoi
- les joueurs sont organisés en poules de 4 maximum [1]. Chaque joueur a un score initial de 100 points.
- dans chaque poule, chaque joueur joue une partie contre chacun des autres.
- Une fois une partie finie, le perdant donne au gagnant 1 point, auquel on ajoute le nombre de fois que le gagnant aurait encore pu bouger un de ses pions. Ce qui revient à transférer des points depuis le score du perdant, vers le score du gagnant.
- Une fois que toutes les parties ont été jouées, on calcule le score de chaque joueur (à l’aide de graphes, ou de tableaux appelés blocs)
- on redistribue alors les joueurs en poules de 1ers, poules de 2e, poules de 3e et poules de 4e.
- On recommence en faisant jouer chaque joueur contre les autres de sa poule [2]
- Les meilleurs scores donnent les joueurs sélectionnés en huitième de finale (ou le meilleur score désigne le champion, selon le temps disponible).
Erreurs
Le tournoi motive les additions et soustractions successives qui sont demandées aux élèves pour actualiser leur score. Cela a donné lieu à des erreurs intéressantes, révélant (entre autres) la fragilité de la soustraction du CE2 au CM2 sans discontinuer.
Graphes
Le principe est de faire, du graphe d’un tétraèdre, un tournoi (théorie des graphes) pondéré par les points gagnés/perdus au cours des parties jouées. Cela suppose que
- chaque joueur ait joué une partie et une seule contre chacun des autres joueurs de sa poule
- chaque partie soit codée par une flèche allant du perdant au gagnant
Ici, clairement, la première contrainte n’a pas été respectée :
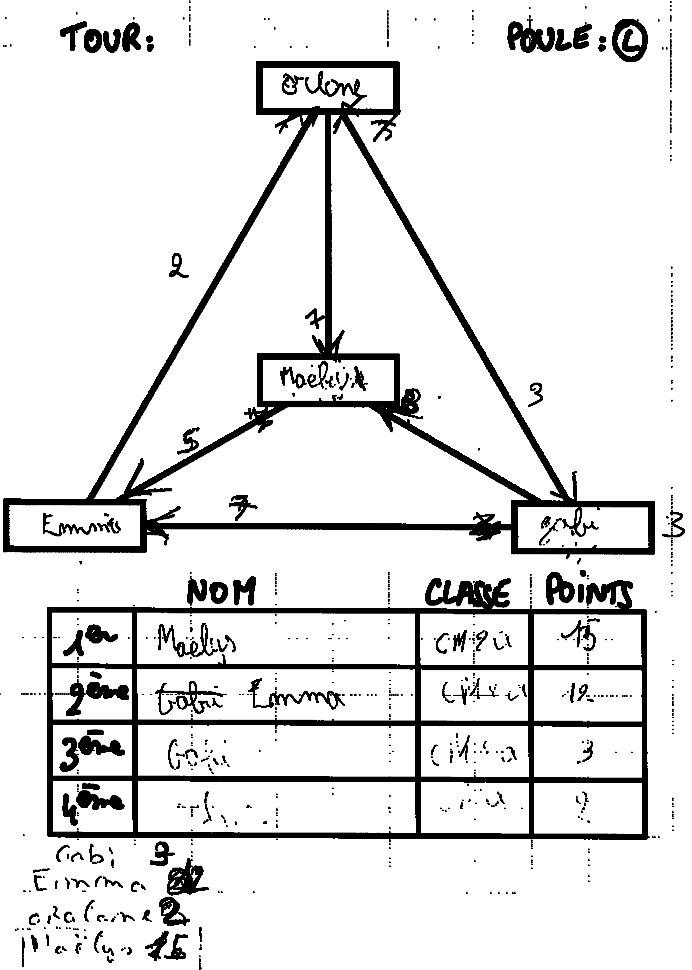
Si un graphe est correctement complété, on peut aisément calculer les scores en soustrayant les nombres sur des flèches issues du sommet du joueur, et en additionnant les nombres sur les flèches allant vers le sommet du joueur. Pour éviter les scores négatifs, on initialise le score de chaque joueur à 100. Des joueurs ont essayé de s’en passer :
- Maẽlys a gagné 7 points contre Orlane et 3 contre Gabi mais perdu 5 points contre Emma. Au total elle a gagné 5 points et son score est devenu 105. Mais elle a marqué 15 points gagnés (erreur de retenue ? de signe ?)
- Emma a gagné 5 points contre Maëlys et 7 contre Gabi mais perdu 2 contre Orlane. Son score a donc au total augmenté de 10 points et est devenu 110. Elle se donne 12 points au lieu de 10 (envie de ne pas compter les termes négatifs). Noter que sans ces erreurs de calcul elle aurait été 1re et non 2e...
- Gabi a gagné 3 points contre Orlane mais les a reperdus contre Maëlys, son score a donc diminué de 7 points (perdus contre Emma) et devrait être 93. À la place on voit 103 (marqué 3).
- Orlane a gagné 2 points contre Emma mais perdu 7 points contre Maëlys et 3 points contre Gabi. Son score devrait donc être 92 soit une baisse de 8 points. À la place, on voit une augmentation de 2 points. Là encore on peut supposer un refus d’additiionner des nombres négatifs.
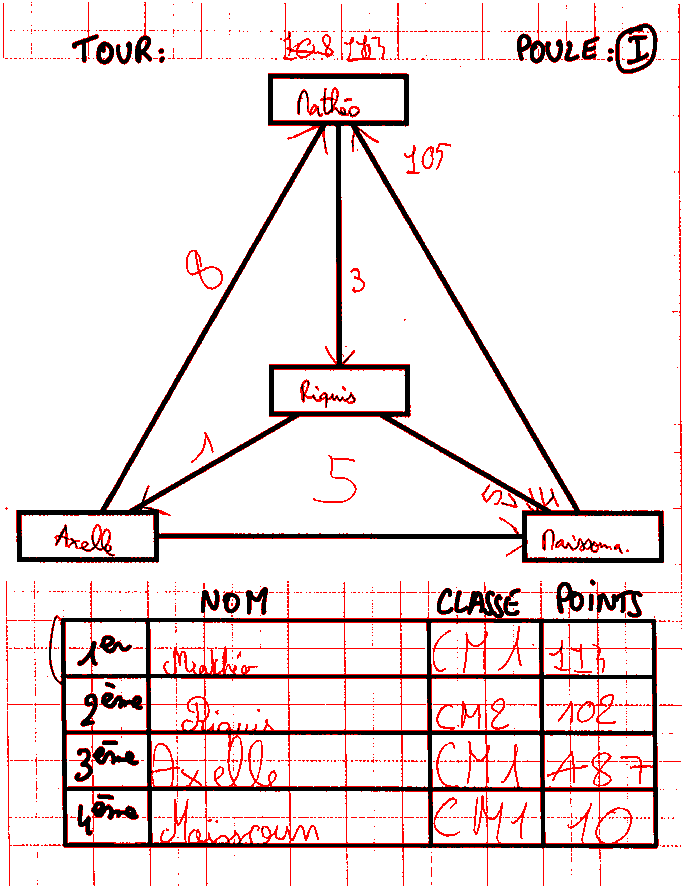
De nombreuses (quoique pas plus qu’avec les blocs, voir plus loin) erreurs de calcul ont été constatées, même en cycle 3. Par exemple, ci-dessous, Riquis, qui a gagné 3 points mais perdu 1 point et 5 points, aurait dû avoir un score de 97 points mais s’est donné 102 points :
Il est probable qu’elle ait oublié de soustraire les 7 points.
Il y a aussi parfois des erreurs sur le nombre de points gagnés/perdus : à alquerkonane, ce nombre est la somme du point du gagnant (parfois oublié) et du nombre de mouvements de pions possibles pour le gagnant. Par exemple, ici, il semble que Kéran ait cru dans un premier temps n’avoir perdu que 8 points contre Thomas, au lieu de 9 :
En effet, 100+7+4-8 = 103 comme indiqué mais une fois le 8 remplacé par un 9, on arrive à 100+7+4-9 = 102 qui n’a pas été corrigé. Le 9 est par contre validé par le recalcul du score de Thomas : 100-4+9+9 = 114 comme indiqué.
Par contre, l’ancien score de Thomas (107, encore lisible sur la feuille) s’explique difficilement (100+9+8 en oubliant le -4 ? Dans ce cas il y aurait eu erreur de retenue). La suite des changements d’état pour Kéran est

ici, c’est le premier qui fait une erreur de signe : au lieu de soustraire les 3 points perdus contre Wayatt, Azur se les additionne :
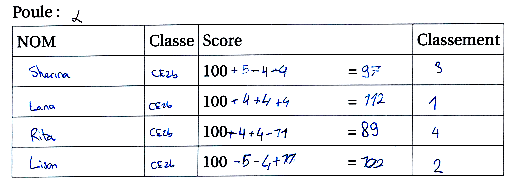
Ici il est possible qu’il y ait juste eu une erreur de signe :
Chaïmila a pu commencer par effectuer 5-4 = 1 puis, au lieu d’ajouter 1 à 100 (ou à 98 si elle avait commencé par soustraire 2), elle l’a soustrait, aboutissant à un total de 97 au lieu de 99. La suite des changements d’états peut lui servir de corrigé :

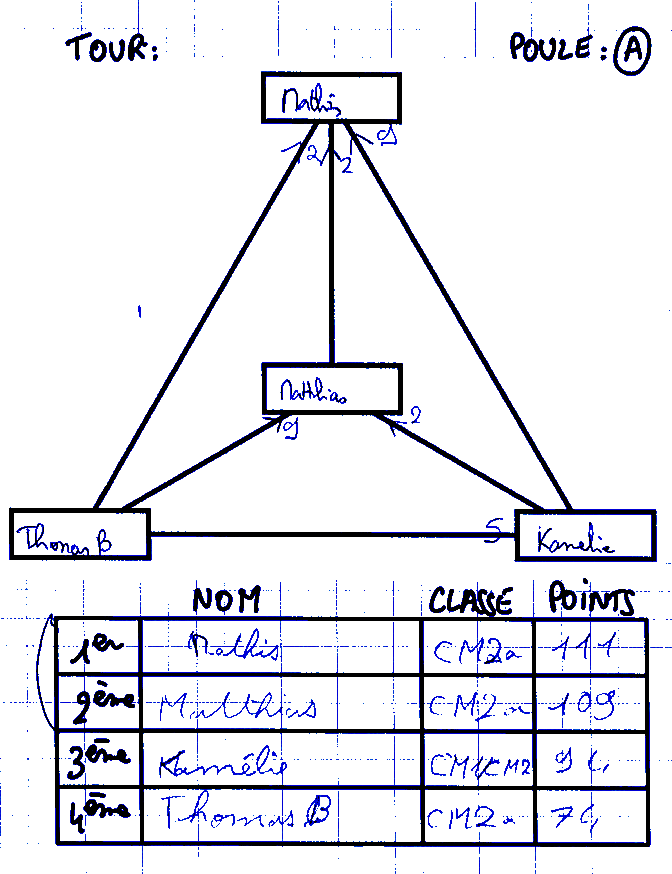
Même le premier (qui n’a en général que des additions à faire) peut se tromper. Ici il s’agit de l’oubli d’un terme :
Mathis a trouvé 111 pour l’addition 100+2+2+9, probablement parce qu’il n’a calculé que 100+2+9 (oubli d’un terme 2). La suite de tous les changements d’états pour Mathis est

Opérations
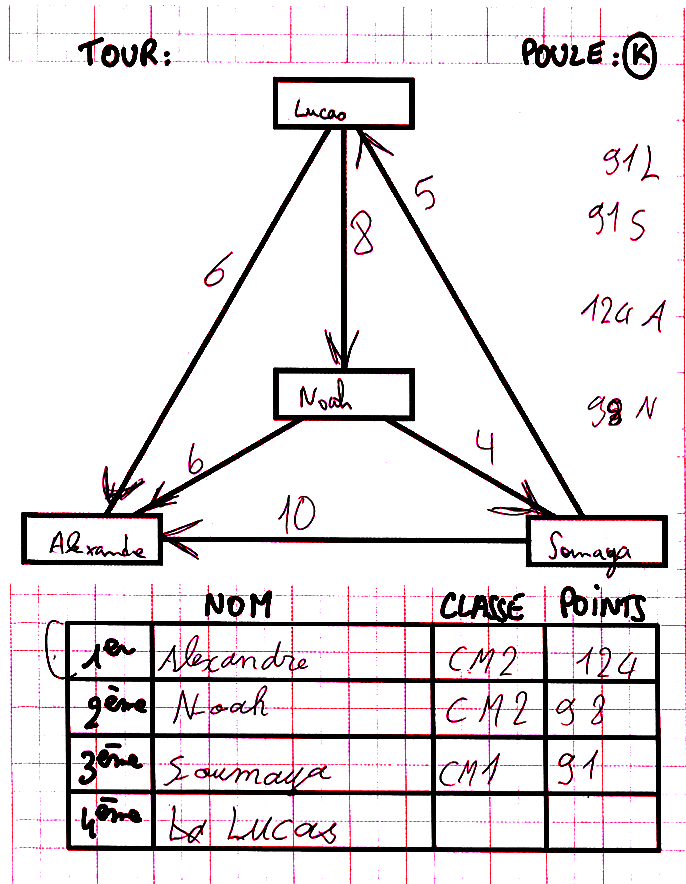
Même sur des additions il y a des erreurs :
Ci-dessus, Alexandre trouve un total de 124 pour 100+6+6+10. On retrouve ce total avec la suite des changements d’état :

Ce cas (erreurs sur des sommes dont tous les termes sont positifs) est cependant plus rare que les erreurs de soustraction. Les erreurs de calcul les plus fréquentes sont celles où il n’y a que des soustractions :
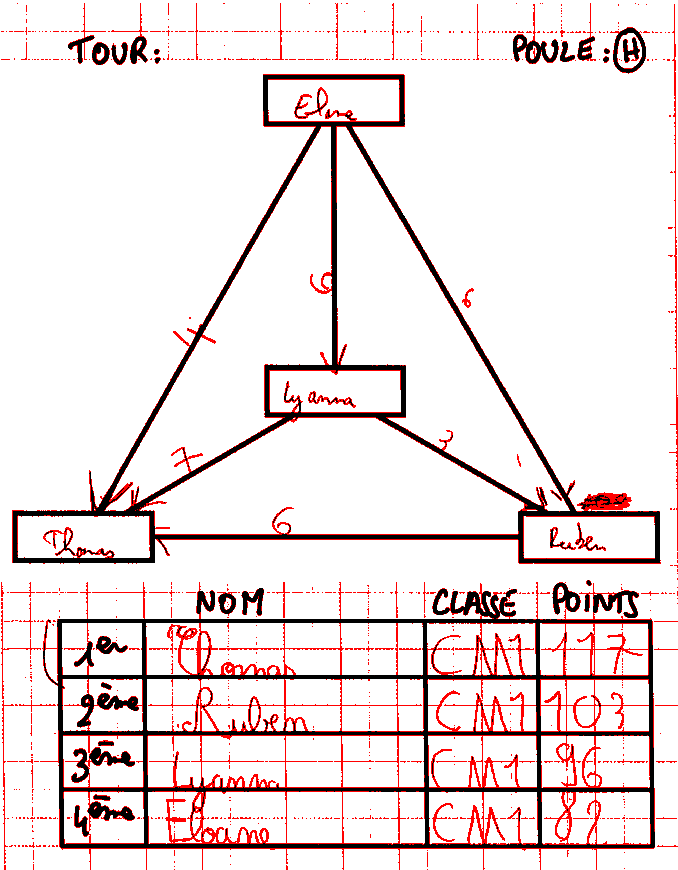
Ci-dessous Eloane doit calculer 100-4-6-6 :
et trouve 88 au lieu de 94 (une troisième soustraction de 6 ?). Voici la suite de ses changements d’état :

Ci-dessous c’est Mahé qui doit calculer 100-6-5-3 :
et trouve 81 au lieu de 86. Voici la suite de ses changements d’état :

Des erreurs arrivent aussi lorsqu’il y a des additions et soustractions combinées. Par exemple ci-dessous Aaron a gagné de 9 points contre Evan, perdu de 2 points contre Gabi et de 4 points contre Wayatt (noter les signes des nombres aux extrémités des flèches) :
100+9-2-4 est égal à 103 mais Aaron a trouvé 102 à la place. Voici un corrigé possible pour lui :

Troncature
L’erreur la plus répandue lorsqu’il s’agit de soustraction, consiste à ne pas effectuer les soustractions (seulement les additions). Ici par exemple Cameron s’est donné un score nul parce qu’il aurait dû soustraire à 100 les nombres 7, 8 et 8 encore :
On peut remarquer qu’il y a eu un consensus tacite (et sans calcul) entre les 3 autres joueurs :
- Orlane a gagné 7 points contre Marie et 7 points également contre Cameron, mais perdu 8 points contre Imane. Ce qui lui fait un score de 100+7+7-8 = 106, et non 116.
- Marie a gagné 8 points contre Imane et 7 points contre Cameron mais les a reperdus contre Orlane, ce qui lui fait un score de 108 et non 116.
- Imane a gagné 8 points contre Cameron et 8 points aussi contre Orlane mais a perdu 8 points contre Marie, ce qui lui fait un score de 100+8+8-8 = 108, et non 116.
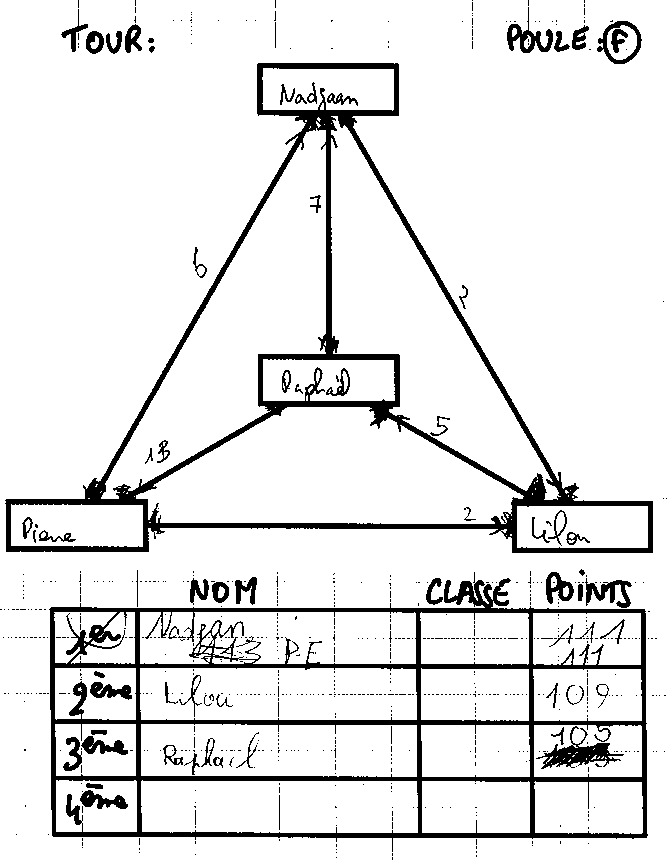
Ci-dessus c’est Pierre qui a renoncé à la place de 3e :
En effet il aurait gagné 13 points [3] contre Raphaël et perdu 6 points contre Nadjan et 2 points contre Lilou, ce qui lui ferait un score de 100+13-6-2 = 105, score qui a été attribué à Raphaël. Celui-ci ayant perdu 13 points contre Pierre et 7 points contre Nadjan, et 5 points contre Lilou, a donc un score de 100-13-7-5 = 75 et non 105.
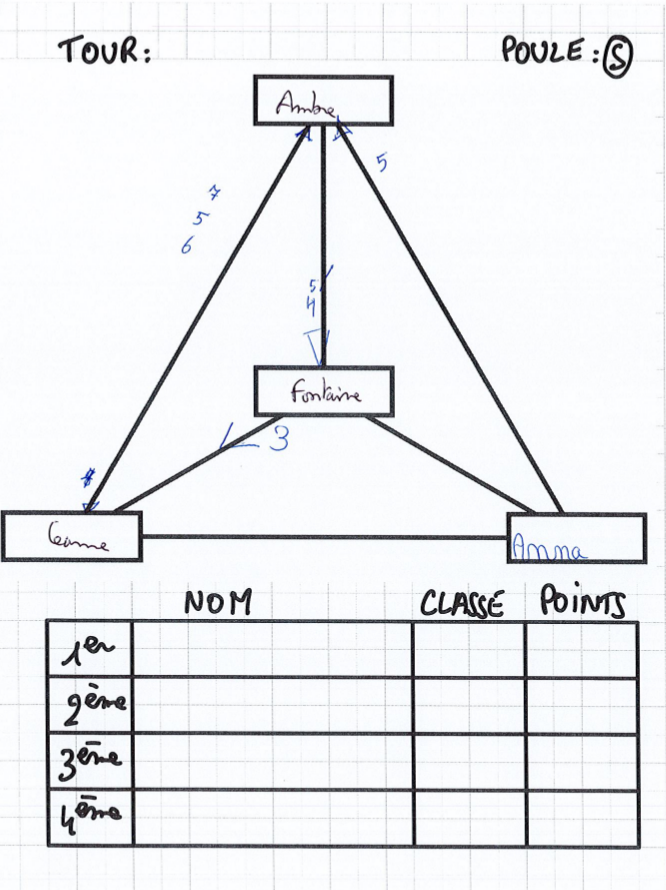
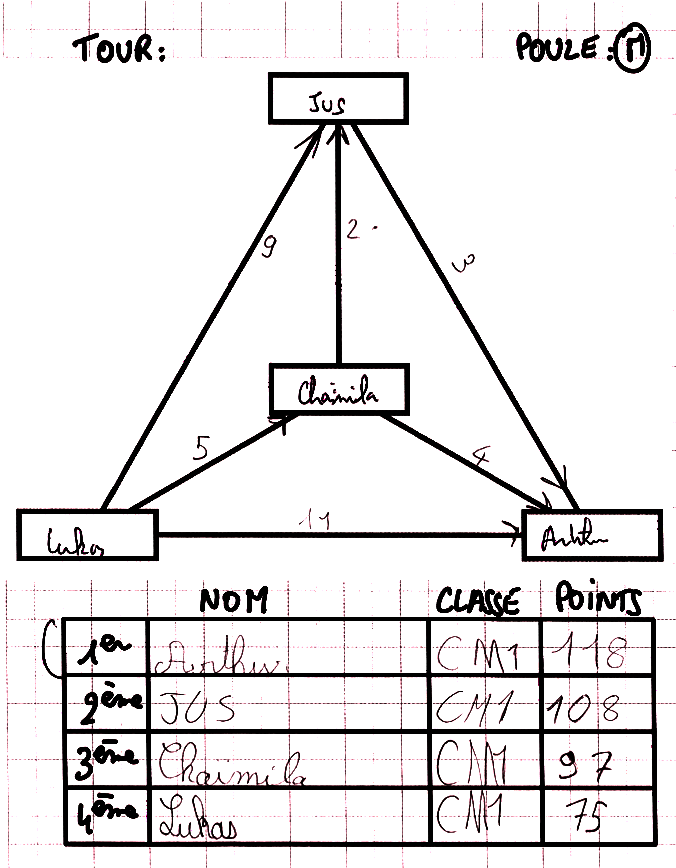
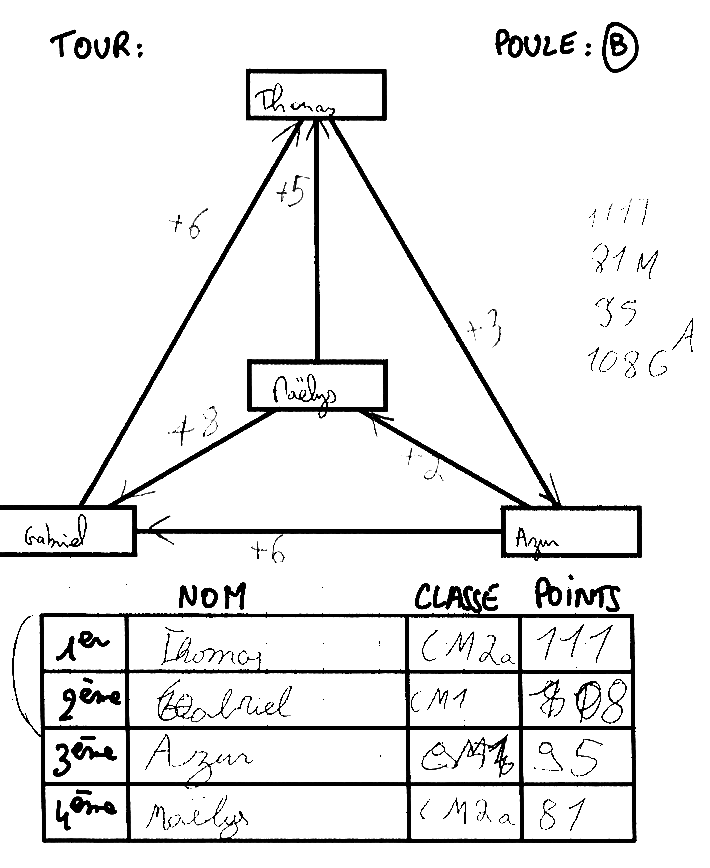
Ici, c’est le premier qui a omis une soustraction :
Thomas a gagné 6 points contre Gabriel et 5 points contre Maëlys mais perdu 3 points contre Azur. Son score devrait donc être 100+6+5-3 = 108, et pas 111 qu’il a obtenu en oubliant de soustraire les 3 points perdus contre Maëlys. Ce qui le met à égalité avec Gabriel qui a correctement calculé son score : 108.
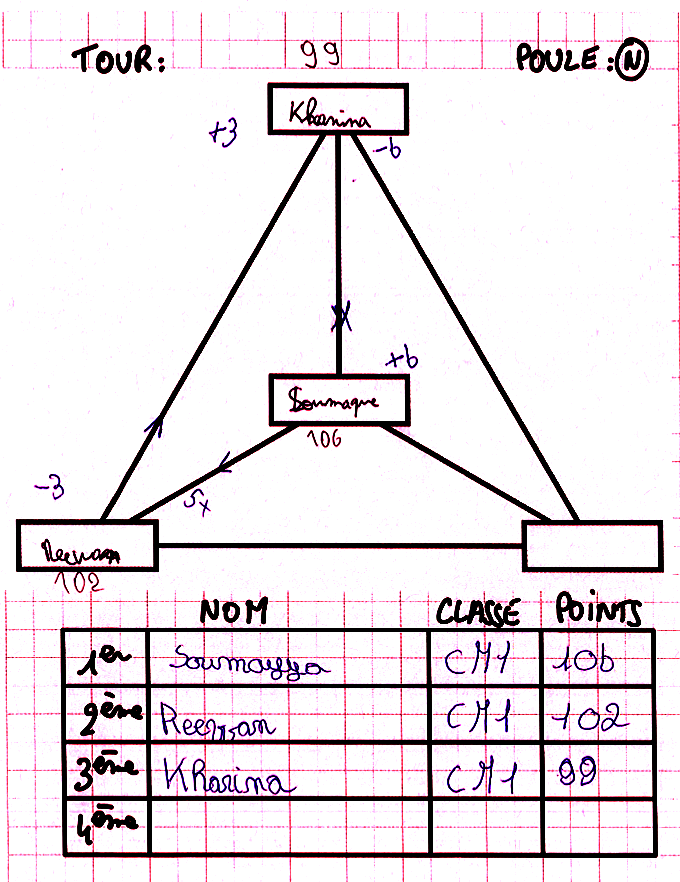
Dans une poule de 3 joueurs, le premier peut faire la même erreur :
Soumayya a gagné 6 points contre Kharina mais en a perdu 5 contre Reewan, ce qui devrait lui donner un score de 100+6-5 = 101 et non 106 qui montre l’oubli de la soustraction de 5. C’est donc Reewan qui aurait dû être premier puisque son score 102 (correctement calculé) est plus grand que 101. Quant à Kharina, elle a gagné 3 points contre Reewan et perdu 6 points contre Soumayya ce qui lui fait un score de 100+3-6 = 97 au lieu de 99 annoncés : encore une erreur de soustraction...
Blocs
On a vu dans les onglets précédents que le calcul de flots dans des graphes n’est pas exempt d’erreurs, surtout lorsqu’il y a des soustractions. En fait, avec les opérations posées en ligne dans des tableaux (appelés blocs plus bas) on retrouve le même genre d’erreurs. Pour commencer, savoir qui gagne des points (addition) et qui en perd (soustraction) n’est pas immédiat :

Ci-dessus les résultats sont corrects mais on voit que la dernière partie, menée entre Baptiste et Lucas, a été corrigée d’erreurs de signe.
Ci-dessous on voit que les élèves ont choisi à un moment de représenter les pertes en rouge et ont d’instinct écrit un signe « plus » avant de corriger celui-ci (Tahïn +2 au lieu de -2, Matthias +4 au lieu de -4) :
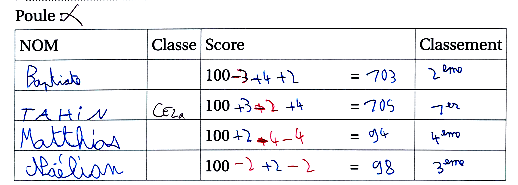
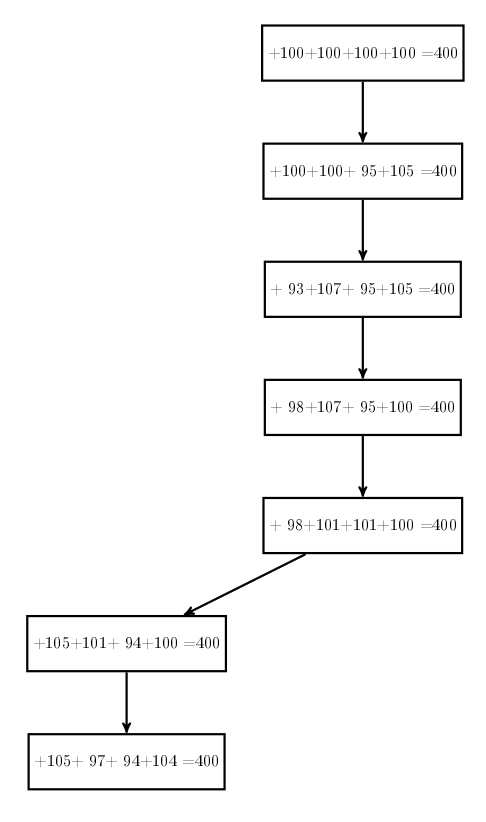
Des élèves de CM2a ont préféré, plutôt qu’écrire le calcul en ligne, rédiger les états successifs :

Les scores affichés sont justes, à part une méprise sur le sens du signe « = » qui devait représenter la somme. On remarque que l’invariant la somme des 4 scores est toujours égale à 400 est vrai, par exemple 95+88+99+118 = 400.
Ci-dessous il y a eu 3 joueurs, et chacun est censé avoir joué une fois et une seule contre chacun des deux autres :

Or si Mahé a gagné 12 points contre Imane, on ne sait pas contre qui Matthis a gagné 3 points, puis 5 points, puis 2 points...
Ci-dessous, de même, Bénédicte s’est ajouté des points sans qu’on puisse savoir contre qui elle les a gagnés :

Mais il est difficile de savoir si c’est de la triche ou seulement des erreurs innocentes de calcul. C’est là qu’on voit l’intérêt de la validation collective des transactions, qui est à la base des cryptomonnaies.
Ci-dessous, il semble y avoir eu une erreur de retenue sur le calcul du score d’Emma :

En effet 100-2+3-7 est égal à 94 et pas à 104. Voici le graphe des changements d’état en guise de corrigé :

Ci-dessous il est clair que Matthis et Orlane ont joué plusieurs parties et que la rotation entre joueurs ne s’est pas faite :

Ci-dessous on remarque deux erreurs intéressantes :
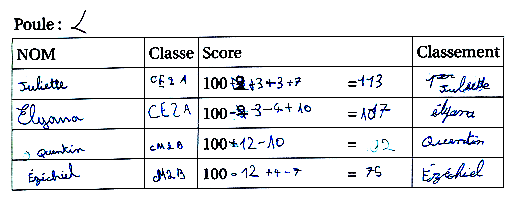
- Elyana trouve 107 comme résultat du calcul 100-3-4+10 (au lieu de 103 ; une probable erreur de signe)
- Ézéchiel trouve 75 comme résultat de 100-12+4-7 (au lieu de 85 : c’est clairement une erreur de retenue). Voici le corrigé :

Mais la plupart des erreurs constatées ont porté sur les soustractions, comme on le verra dans l’onglet suivant.
Soustractions
Voilà un bloc mystérieux :

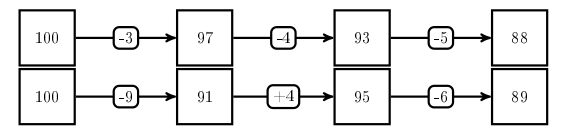
En effet on y trouve le même résultat 89 pour deux opérations différentes 100-3-9-6 et 100-3-2-6. De fait, la première donne 88 et non 89 :

Ici les deux derniers ont fait des erreurs de soustraction :

- Pablo trouve 96 pour 100-9+4-6 (au lieu de 89)
- Ethan trouve 92 pour 100-3-4-5 (au lieu de 88)
Voici leurs évolutions simultanées :
Ci-dessous on voit une erreur de soustraction sur le score de Tahïn (trois nombres à soustraire) :

En effet 100-8-9-2 n’est pas égal à 92 mais à 81 :

On voit d’autres erreurs, corrigées par la suite. Ce qui montre l’intérêt de cette activité qui favorise le tutorat entre pairs.
Ci-dessous on voit deux erreurs dans le calcul du score de Nohéline :

- D’une part le résultat du calcul 100-7+3+2 n’est pas 105 mais 98,
- d’autre part le +3 correspond à un +3 (score de Thomas) et pas à un -3.
Donc, ou bien Thomas avait perdu et son score devrait alors être 100-4-3-2 = 91 au lieu de 97, ou bien Nohéline a un score de 100-7-3+2 = 92 qui la plaçait en dernière position de la poule, et non en pénultième.
Dans le cas du tournoi où seul compte le classement dans la poule, ce n’est pas grave tant que les élèves trouvent un classement consensuel, mais s’il faut un certificat, celui-ci est impossible à donner car la somme des 4 scores est 97+100+111+105=413 au lieu de 400. L’équivalent de cette vérification dans les cryptomonnaies s’appelle le hash de la transaction.
Ci-dessous on voit plusieurs erreurs :
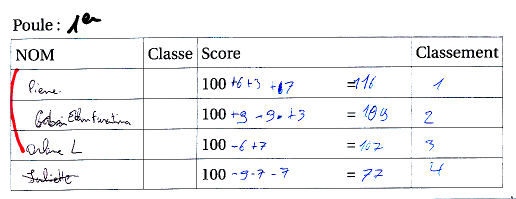
- Le score d’Orlane 100-6+7 est évalué à 107 au lieu de 101 (comme avec les graphes, oubli de soustraire)
- Orlane, qui a visiblement perdu 3 points contre Ethan, ne les a pas écrits sur la feuille, ce qui fait que son score réel est 100-6+7-3 = 98
- Ethan évalue son score 100+9-9+3 à 109 au lieu de 103
On voit une tendance générale à éviter les soustractions.
Notion de bloc
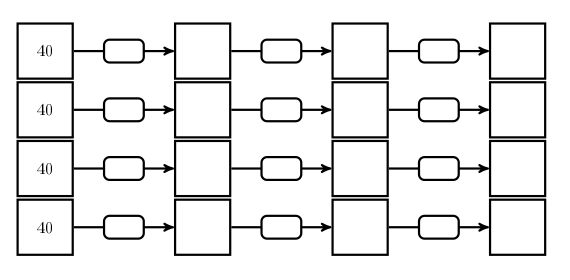
Un bloc (pour une poule de 4) est un graphe de ce genre (partiellement rempli) :
Note : un clic sur l’image ci-dessus permet de télécharger un document pdf contenant 2 blocs vierges et permettant donc de gérer l’historique de 2 poules d’alquerkonane. On a choisi d’initialiser les scores à 40 plutôt que 100 parce que, sans tricher, il ne semble pas possible de gagner de plus de 12 points sur un damier 6×4, et en 3 parties il n’y a pas de risque d’aboutir à un score négatif si le score initial est supérieur à 36.
Un bloc va typiquement évoluer au cours du jeu, puisqu’après chaque partie il y a deux scores qui sont mis à jour :

Historique
On représente les états successifs d’un bloc par un graphe orienté, chaque état du bloc étant représenté par un sommet du graphe, et chaque modification du bloc (transaction) étant représentée par une flèche allant de l’ancien état au nouvel état.
tableaux
Dans une première version, on recopie les tableaux tels quels dans les sommets du graphe, sauf dans le dernier où on fait le bilan :
Somme toute (!), plutôt que valider une seule fois à la fin, pourquoi pas valider au fur et à mesure ? On obtient alors des blocs où seuls figurent les scores actualisés des 4 joueurs (onglet suivant).
bilans
Pour la sécurité des transactions, il faut garder dans les blocs un maximum d’informations, mais on peut n’afficher que les scores des joueurs, ce qui simplifie le dessin des blocs :
Noter qu’il est possible de retrouver les détails des parties jouées, par soustractions. Par exemple la dernière flèche ci-dessus indique (par soustractions) que le deuxième joueur a gagné de 104-101 = 3 points et que le troisième joueur a gagné de 86-89 = -3 points, c’est-à-dire perdu de 3 points.
en ligne
On gagne encore un peu de place en écrivant les 4 scores, non plus l’un en-dessous de l’autre, mais l’un à côté de l’autre, séparés par des petites croix en forme de « + » :
On choisit de mettre également un « + » devant le tout, pour rappeler que les scores sont tous positifs, y compris le score du premier joueur.
hash
Pour être complet, on choisit d’ajouter à la version de l’onglet précédent, la somme de contrôle (c’est pour cela qu’on avait mis des « + », ils incitent à additionner) :
C’est ainsi qu’on dessinera les blocs dans la suite de l’article.
Du bloc à la chaîne de blocs
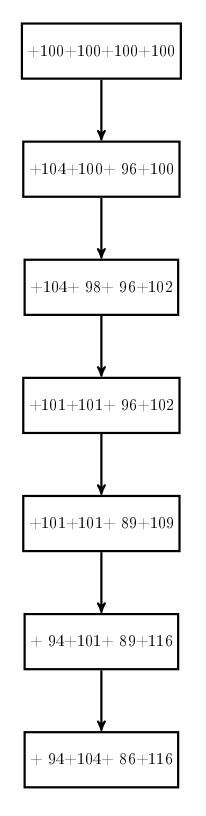
Voici un exemple de bloc correct mais pas du premier coup. Il permet de retracer un historique intéressant :

Erreurs ligne 1
On voit que le +2 a été transformé en -2 puis qu’un +7 a été ajouté. Dans les onglets suivants on examine les conséquences de ces faits sur la structure de la chaîne de blocs qui devient par moments arborescente.
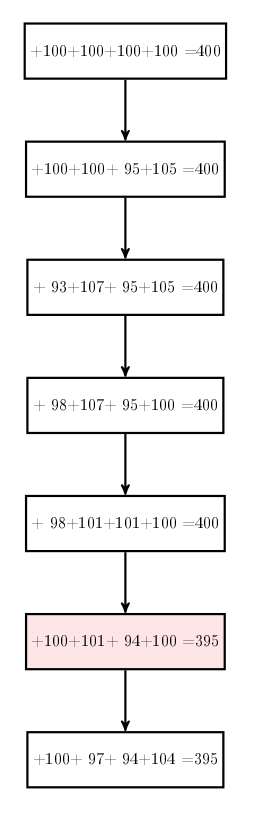
Avec +2
Lorsque les 6 jeux sont finis, on constate que la somme des scores n’est plus égale à 400. Ce n’est pas le fait du dernier transfert (de 4 points) puisque juste avant, le total n’était déjà plus de 400 (en rouge) :
L’erreur vient du premier joueur qui comprend qu’il n’a pas gagné 2 points. Il suppose (en barrant le « + » devant le 2) qu’en fait il a perdu ces 2 points.
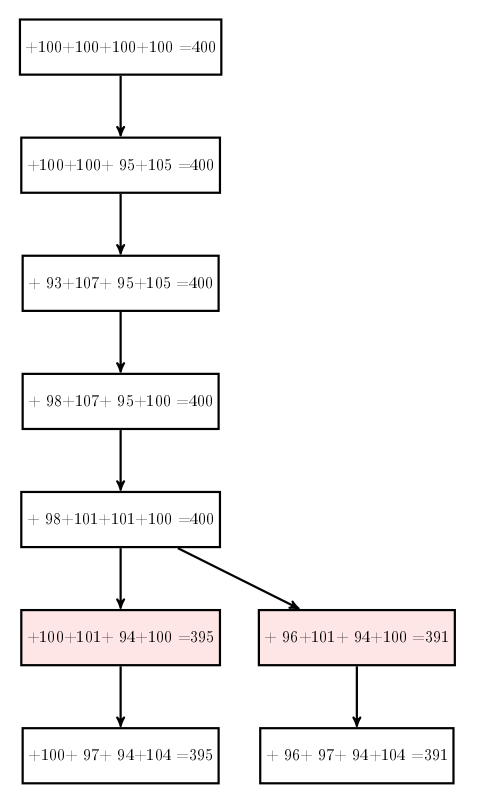
Avec -2
Alors on ajoute une autre chaîne de blocs, où le +2 est remplacé par -2, la dernière transaction étant également appliquée à cette nouvelle chaîne :
Mais dans la nouvelle chaîne (branche droite) le total n’est toujours pas égal à 400. Là encore, ce n’est pas la transaction de 4 points qui est fautive mais le -2 (en rouge).
Avec +7
On commence par élaguer l’arbre (enlever l’ancien chaîne fautive puisqu’on a compris qu’elle n’est pas bonne) et on branche sur le bloc fautif un correctif +7 (pour le premier joueur) :
On réessaye d’enregistrer sur cette nouvelle branche le transfert de 4 points :
Mais le total n’est toujours pas 400 ; en effet c’est le -2 qui était fautif, le +7 ne le corrige pas (en rouge).
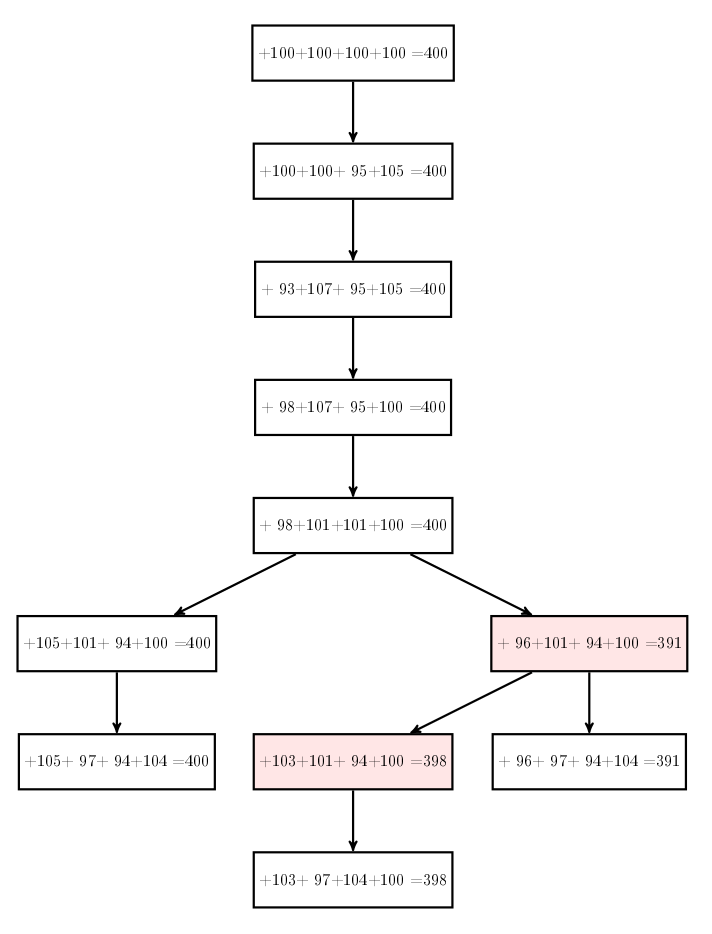
Sans -2
Le branchement de la transaction +7 ne doit donc pas être fait après la transaction -2, mais à la place :
On constate que l’une des feuilles de l’arbre est correcte (somme égale à 400) donc on la valide collectivement en élaguant les branches fautives : un arbre à une seule branche s’appelle une chaîne
Cryptomonnaies
Pour occuper les concurrents rapidement éliminés du tournoi, on peut leur proposer de résoudre des problèmes portant sur alquerkonane, du type de ceux présentés dans le livret d’exercices ci-dessous :
Pour chacun des exercices proposés, le premier qui a trouvé la solution se voit (après validation de la solution par ses camarades) attribuer un certain nombre de points dépendant de la difficulté de l’exercice, et cela peut remonter son score suffisamment pour qu’il puisse à nouveau entrer dans la lice. Le principe est qu’il est aisé de vérifier que la solution est bonne, mais plus long de trouver la solution. Et la solution est validée par l’ensemble des membre de la chaîne de blocs, ce qui est le principe de fonctionnement du minage de cryptomonnaie : on réinjecte des points dans le tournoi, avec l’accord des pairs.
Note : la question des cryptomonnaies a été abordée au bac 2024 :












Commentaires