En 1713, Nicolas Bernoulli publie un essai de son oncle Jacques Bernoulli, titré Ars Conjectandi (l’art de la conjecture), en latin, où il expose l’application des probabilités à la modélisation de la recherche scientifique. Dans cet ouvrage, Bernoulli pose, entre autres, le « problème inverse » :
Une urne contient des boules blanches et noires ; la proportion p de boules blanches est inconnue. On extrait de l’urne n boules (par exemple, avec remise) et on constate que k d’entre elles sont blanches. Que peut-on inférer sur le nombre p à partir de n et k ?
Autrement dit, Bernoulli demande la loi de p, à partir des données expérimentales disponibles (sondage de sortie d’urne). Comme on le verra plus bas, c’est Bayes qui a été le premier à résoudre ce problème. Mais Bernoulli progresse sur le problème direct qui consiste à calculer la loi du nombre de boules blanches : C’est la loi binomiale, dûe à Jacques Bernoulli.
En 1718, Abraham de Moivre publie the Doctrine of Chances dans lequel il cherche à résoudre le problème inverse par une sorte d’intervalle de confiance. Pour cela il avait besoin d’une approximation de la loi binomiale par une loi continue. Et comme des factorielles interviennent dans le calcul des coefficients binomiaux, de Moivre demande à James Stirling une telle approximation. Puis utilise la formule de Stirling pour obtenir la loi normale.
En 1728, Leonhard Euler a démarré des recherches similaires à celles de Stirling, sur l’interpolation de la factorielle. Il créa alors la fonction gamma, et au passage, en calculant des intégrales à l’aide de celle-ci, la fonction bêta. Or c’est justement la loi bêta, issue de ces recherches, qui sera la solution fournie par Bayes, au problème inverse de Bernoulli.
Il est difficile de savoir quand exactement Thomas Bayes a résolu le problème inverse. Sa solution a été publiée en 1763 dans les compte-rendus de la société philosophique royale de Londres, mais c’est son ami Richard Price qui a publié l’article au nom de Bayes, alors décédé, après avoir quelque peu complété l’article.
En 1774, Pierre-Simon de Laplace publie un Essai philosophique sur les probabilités, dans lequel figure la définition d’une probabilité conditionnelle qui figure plus bas dans cet article, et qui ressemble beaucoup à la traduction du texte de Bayes. Selon wikipedia, ce serait « sans être probablement au courant du travail (publié en 1763) de Thomas Bayes (mort en 1761) ». Qu’il soit ici permis d’en douter, puisque Laplace cite l’exemple de la probabilité que le soleil se lève demain, comme l’avait fait Price (en se reférant à Bayes).
En 1812, Laplace publie Théorie analytique des probabilités, un immense traité, considéré encore aujourd’hui comme fondamental en probabilités. On y retrouve bien entendu la définition des probabilités conditionnelles et la résolution du problème inverse.
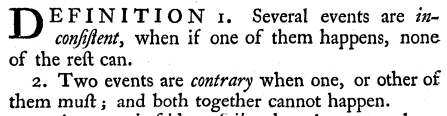






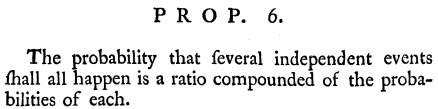


Commentaires