Partie A
Question 1
a
L’arbre pondéré peut se construire avec le fichier ci-dessous [1]
Pour télécharger l’outil (ou l’ouvrir dans un autre onglet), cliquer droit sur l’image ci-dessous :
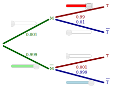
Pour construire l’arbre, il suffit donc de manipuler les curseurs en lisant l’énoncé ; on devrait obtenir ceci :
b
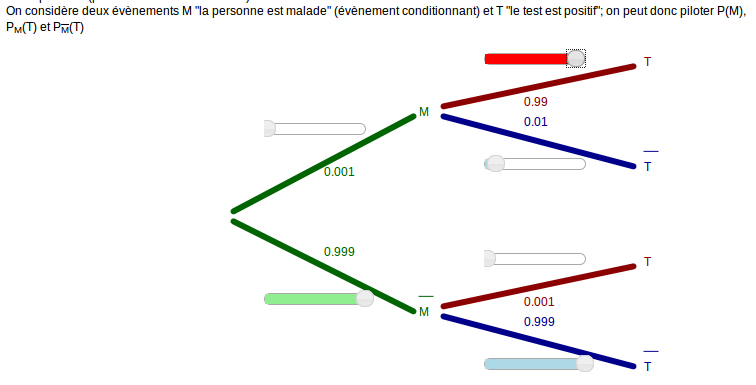
Les calculs sont juste en-dessous de l’arbre pondéré :

c
En fait, non puisque le résultat est légèrement supérieur à « une chance sur deux » :

Question 2
Une fois que ce qui précède a été fait, il suffit de manipuler le curseur en haut à gauche (M) jusqu’à ce que l’affichage de la probabilité conditionnelle tout en bas dépasse 0,95 ; on trouve x environ 0,016 :
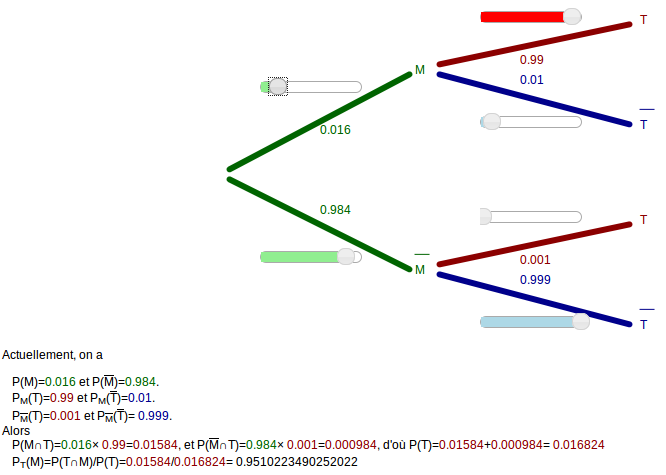
L’arbre pondéré en ligne :
Arbre pondéré (pour l'exercice 2 bac S 2014)
On considère deux évènements M "la personne est malade" (évènement conditionnant) et T "le test est positif"; on peut donc piloter P(M), PM(T) et P(T)
Actuellement, on a
- P(M)= et P()=.
- PM(T)= et PM()=.
- P(T)= et P()= .
- P(M∩T)=× =, et P(∩T)=× =, d'où P(T)=+=
- PT(M)=P(T∩M)/P(T)=/=
Partie B
Question 1
a
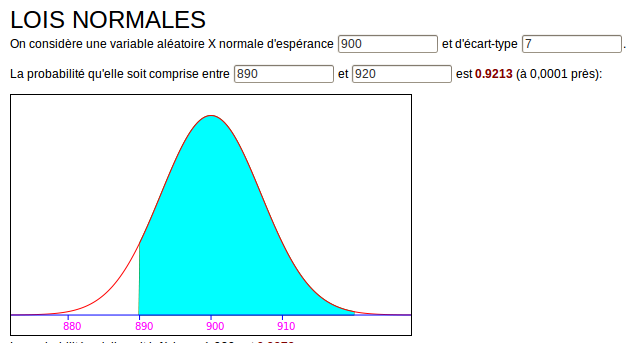
On demande de calculer une probabilité normale ; le calculateur de lois normales est donc sollicité pour cela. On entre les paramètres suivants :
- 900 pour l’espérance
- 7 pour l’écart-type
- 890 et 920 pour les bornes de l’intervalle
La probabilité apparaît alors [2] [3], ainsi qu’un graphique montrant l’asymétrie de l’intervalle :
b
L’interactivité de l’outil en ligne permet de rapidement tâtonner pour plusieurs valeurs de h (qui doivent être entières d’après l’énoncé) :
18 est trop petit :
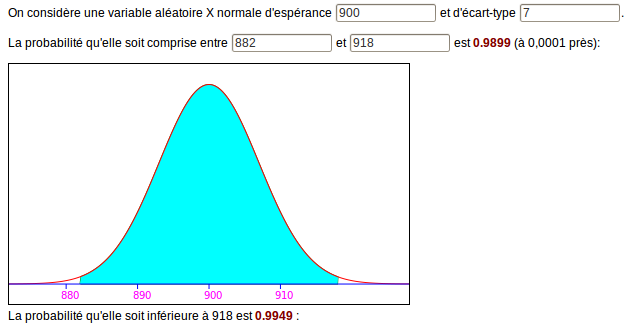
Et 19 est trop grand :
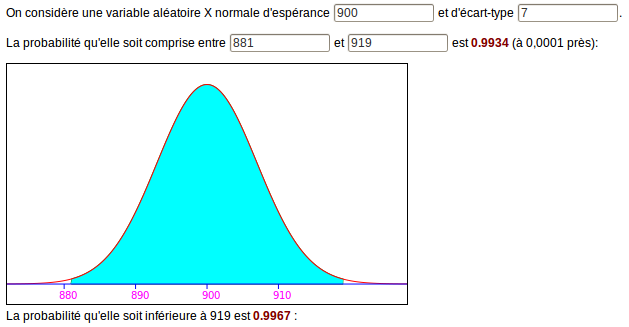
Mais un seul des deux donne une probabilité de 0,99 à un millième près, ce qui répond à la question [4].
Variante
On pouvait aussi chercher une loi binomiale ayant pour espérance 900 et pour écart-type 7. On trouve environ 952 et 0,9455555 pour paramètres [5]. On ouvre le calculateur d’intervalle de fluctuation et on entre ces deux valeurs pour paramètres...
Question 2
Comme le suggère l’énoncé, on peut utiliser un intervalle de fluctuation asymptotique à 95%. Pour cela, on va ouvrir l’outil adéquat, et entrer les paramètres suivants :
- 1000 pour la taille de l’échantillon
- 0,97 pour la probabilité de succès
L’intervalle de fluctuation asymptotique est non seulement calculé [6] mais aussi dessiné :

Puis on calcule le nombre de succès dans l’échantillon (1000-53=947) et on entre ce nombre pour avoir la réponse (« refusé » veut dire « oui » !) :

Variantes :
On pouvait aussi intervertir les succès et échecs afin d’éviter de faire la soustraction à 1000. Dans ce cas la probabilité de succès n’est plus 0,97 mais 0,03. Et la réponse est évidemment la même qu’auparavant :

On pouvait aussi (le « on pourra » de l’énoncé disait que l’intervalle de fluctuation asymptotique n’était pas obligatoire) utiliser un intervalle de fluctuation, basé sur une loi binomiale de paramètres 1000 et 0,03 :
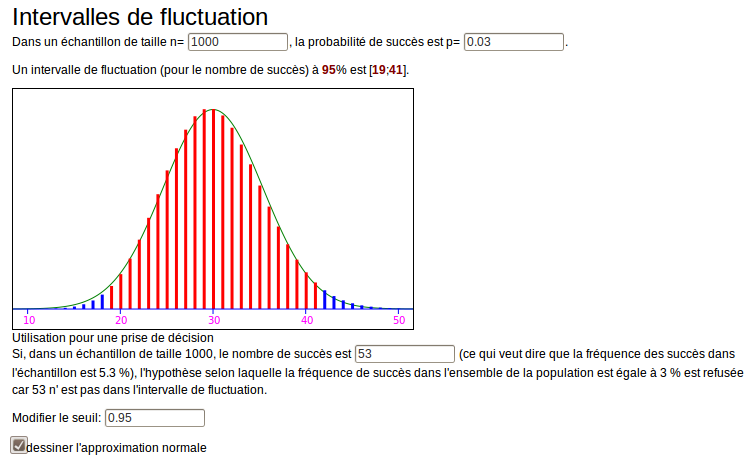
Les calculs sont plus longs dans ce cas, ce qui montre l’intérêt de l’intervalle de fluctuation asymptotique...


Commentaires