
Activité
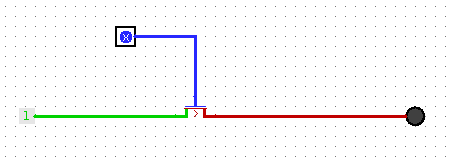
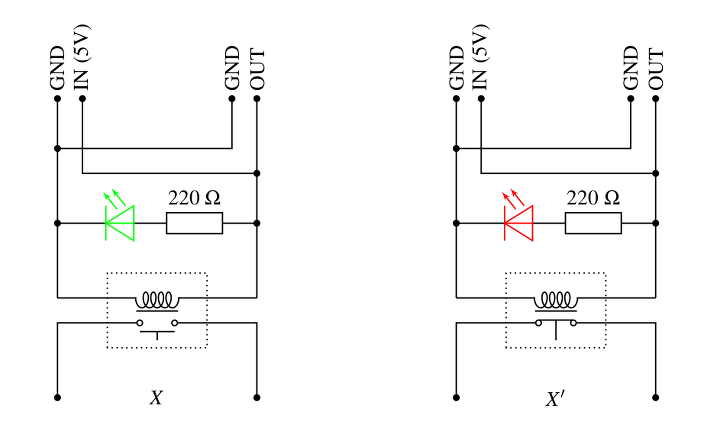
L’activité la plus simple consiste à faire manipuler un seul relais (inverseur) dont le courant d’entrée dépend d’un interrupteur marqué 0-1, de ce genre :
01
et dont la sortie alimente une lampe à filament capable de supporter la tension plus élevée que requiert le relais dans son fonctionnement.
On constate alors que la lampe s’allume uniquement lorsque le courant d’entrée ne circule pas dans le relais : on a réalisé une porte non, dont voici la table de vérité :
| courant d’entrée | allumage de la lampe |
| 0 | 1 |
| 1 | 0 |
Conjonction
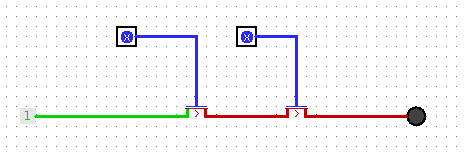
Pour la porte et, il faut deux interrupteurs (puisqu’il y a deux opérandes) :

(à gauche, les câbles alimentant les deux relais montés en série)
En faisant la table de vérité, on constate que la lampe ne s’allume que lorsque les deux interrupteurs sont sur « 1 » :

Ce qui donne cette table de vérité :
| entrée 1 | entrée 2 | sortie |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Ce résultat est logique, puisque comme les deux relais sont en série, le courant ne passe au travers du montage que s’il peut traverser le premier relais et le second relais.
Disjonction
Pour la disjonction, on monte les relais en parallèle, ce qui fait que le courant passe dès qu’il peut traverser le premier relais ou le second relais. Ce qui donne cette table de vérité :
| entrée 1 | entrée 2 | sortie |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Ou exclusif
Ce montage est plus complexe que les précédents :

Il est formé de deux parties, reliées en parallèle :
- un relais normal commandé par la première entrée, en série avec un relais inverseur commandé par la seconde entrée,
- un relais inverseur commandé par la première entrée, en série avec un relais normal commandé par la seconde entrée.
On constate que la lampe ne s’allume que si les deux interrupteurs donnent des valeurs différentes :

La configuration ci-dessus a par exemple pour effet d’allumer la lampe :

En résumé, la table de vérité de cette opération est
| entrée 1 | entrée 2 | sortie |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Addition
On constate en regardant les montages précédents que
- le chiffre des unités pour l’addition 1 bit est donné par xor (ou exclusif)
- le chiffre des deuzaines (ou la retenue) est donné par une porte et.
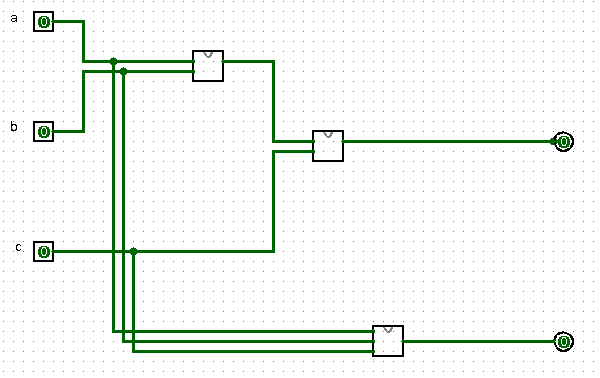
Il est possible de réaliser un additionneur binaire avec 5 relais (dont deux inverseurs) :

On aperçoit à gauche la lampe des deuzaines et en bas à droite, celle des unités. La table de vérité correspond bien à une addition binaire :
- 0+0 = 00

- 0+1 = 01

- 1+0 = 01

- 1+1 = 10

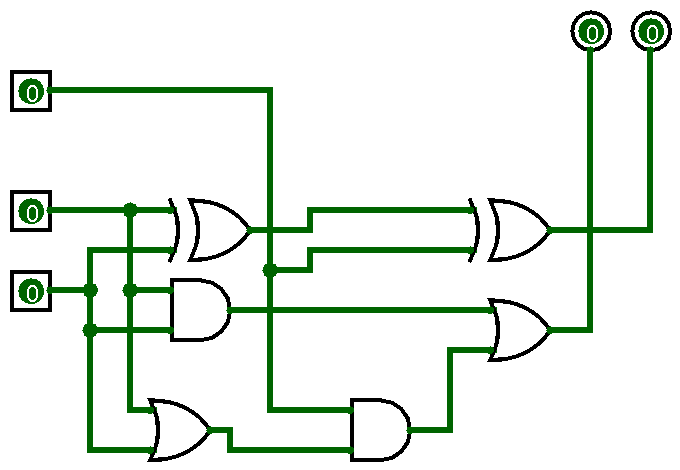
On a donc, avec les circuits précédents, la base d’un additionneur :
- on utilise un xor entre les deux entrées
- on fait encore un xor mais entre la somme et le retenue d’entrée : en sortie on a le bit de la somme
- on réalise une opération de majorité entre les 3 entrées (les deux bits d’entrée et la retenue entrée) pour avoir la retenue engendrée : il y a une retenue uniquement si parmi les 3 entrées, au moins deux d’entre elles étaient à 1.
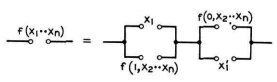
Pour chercher une porte majorité parmi 3, on peut utiliser encore une fois la figure 4 de Shannon :
- Si a=0, la majorité entre a, b et c est b et c (1 seulement si b=1 et c=1)
- Si a=1, la majorité entre a, b et c est b ou c.
La construction a été donnée sous la forme d’un devoir maison à faire avec le logiciel Logisim. Voici des copies d’élèves de 1re NSI (les images sont cliquables et permettent de télécharger leurs circuits) :
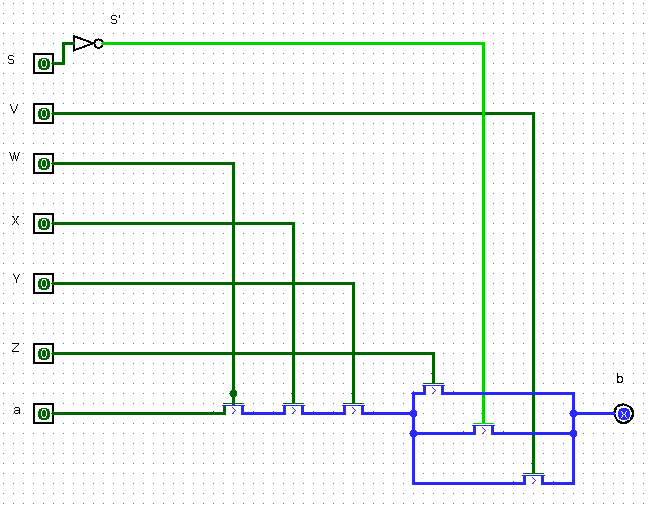
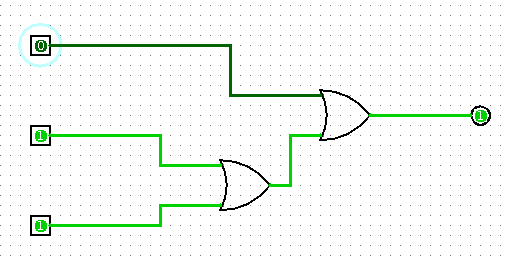
Pour le corrigé, on programme de façon modulaire, en commençant par remarquer qu’il est possible de relier trois relais en parallèle ou de faire ainsi :
On dispose alors d’une porte ou à trois entrées, dont la sortie est 1 dès qu’au moins une des trois entrées est 1. On peut s’en servir pour faire un additionneur 1 bit avec retenue :
Quartets
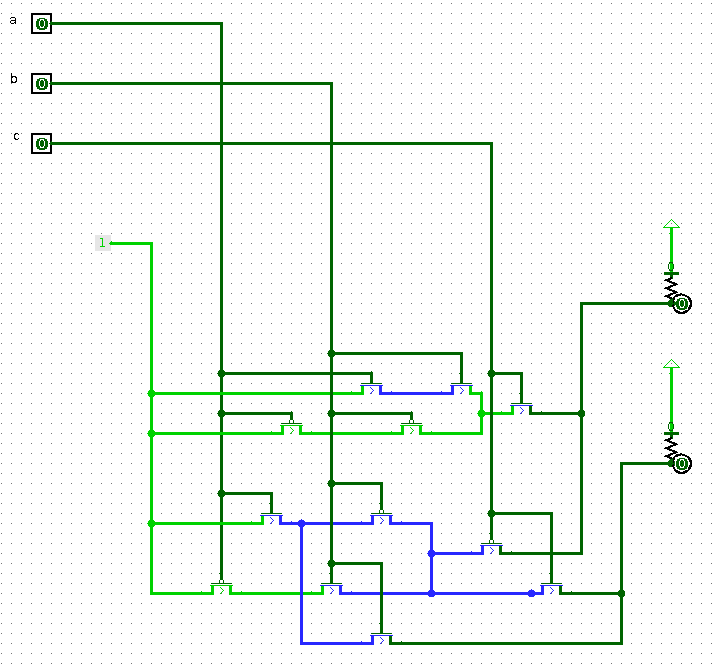
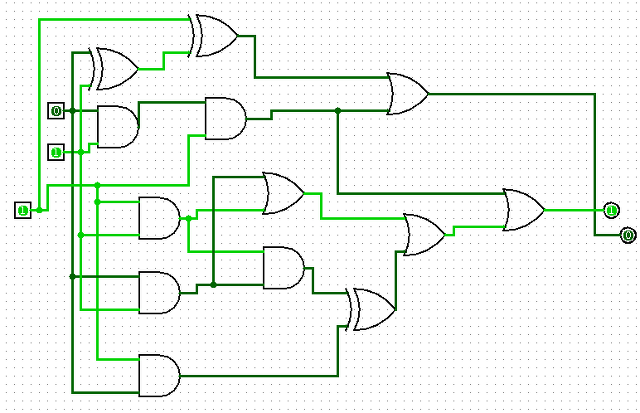
Dès la rentrée 2023, un élève de 1re NSI a créé un circuit à 6 portes (à deux entrées chacune) réalisant l’addition binaire de trois nombres à un chiffre (dont l’un est la retenue) :
Le circuit obtenu alors est un additionneur, mais sur 1 bit :
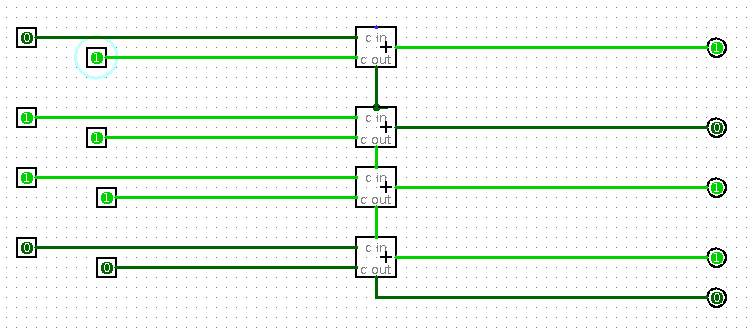
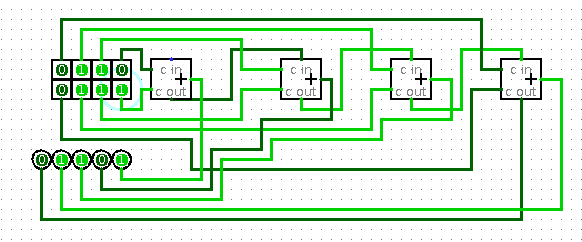
Maintenant il suffit d’en relier 4 en cascade pour avoir un additionneur 4 bits :
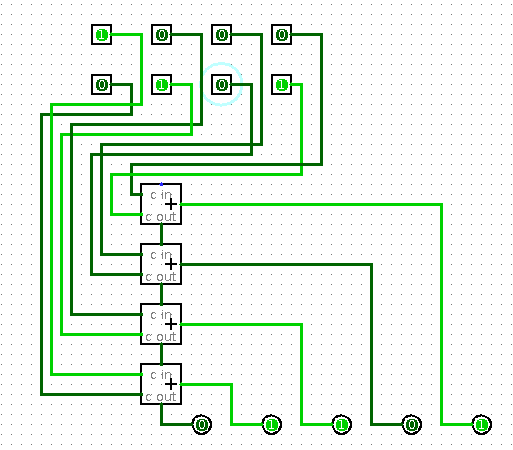
Produire cet additionneur d’octets a été donné en devoir sur Moodle. Tout le monde n’a pas réussi. Par exemple il y a eu des tentatives de brancher plusieurs entrées binaires sur un même point du circuit, ce que Logisim affiche en rouge (et le circuit ne fonctionne pas). Mais le principal problème a été le placement des 8 bits d’entrée et des 5 bits de sortie de manière qu’on reconnaisse les nombres :
La séparation des quartets résout partiellement ce problème :
Le rajout de texte dans le circuit, également :
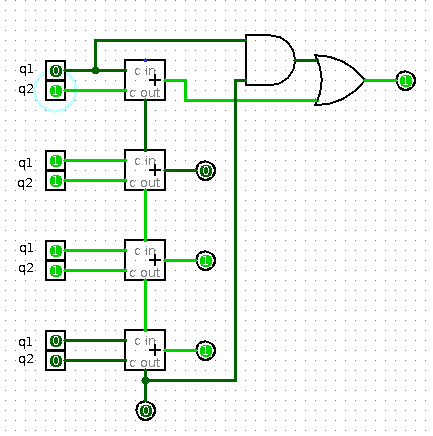
Mais un élève a rapidement produit ce circuit très ergonomique :
(on voit que 6+7==13)
Expérimentation en STI2D
Manipuler-Représenter
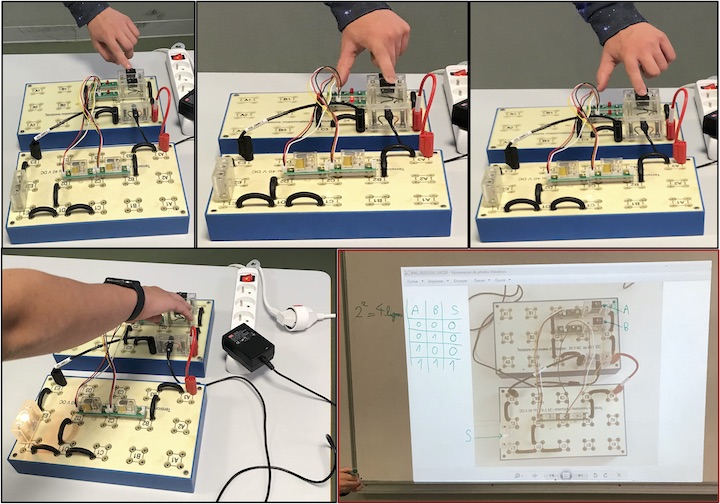
Après repérage des 2 entrées A & B (interrupteurs) et de la sortie S ( lampe) , l’élève dresse la table de vérité incomplète.

L’élève manipule les 2 interrupteurs en faisant varier les positions I/O et complète la table de vérité (truth table).
Abstraction
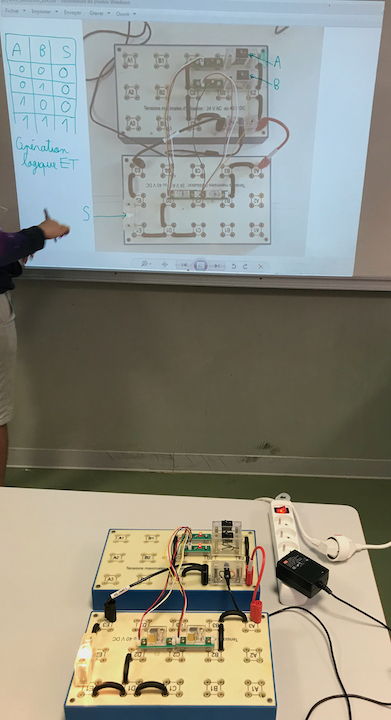
L’élève constate que la lampe s’allume (S=1) lorsque les 2 interrupteurs A & B sont fermés (position I). Cette opération logique est exprimée à l’aide de la fonction logique ET.

















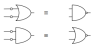

Commentaires