Les ovnis étant de technologie extraterrestre, peuvent s’interpénétrer et le croisement se fera sans collision. Les ovnis n’étant pas transparents, on ne sait pas ce qu’il advient de leurs occupants au moment du croisement...

Fabrication d’un ovni

Les étapes suivantes ont été effectuées au préalable sous Blender 3D :

• effaçage du cube
• création d’un « plan » (quadrilatère) en vue de dessus
• suppression de ses sommets (après les avoir tous sélectionnés en faisant « a » deux fois)
• création d’un sommet près de l’axe avec un « control-clic »
• création des autres sommets donnant le profil de l’ovni (en fait la moitié), par d’autres control-clics
• désélection de tous les sommets avec « a »
• sélection des sommets, l’un après l’autre, avec « b » puis dessin d’un rectangle de sélection ; mouvement avec « g » puis la souris, pour affiner le profilage de l’ovni ;
• utilisation de l’outil « spin » après avoir sélectionné tous les sommets (avec « a ») ; 20 divisions et un angle total de 360°.
• position de l’ovni à (0,0,0) et réglage de la taille avec « s » puis la souris
• application à l’ovni d’un « material » de couleur bleue, avec une couleur « spéculaire » bleue claire (et l’algorithme de Phong)
• remplacement de la lumière par une lumière de type « sun » placée au-dessus de l’ovni et dirigée vers celui-ci
• déplacement de l’appareil photo (« camera ») près de l’axe des x, tournée vers les grandes valeurs de x

Le résultat, vu de dessus (la lumière est représentée en pointillés et la caméra est représentée par une pyramide tournée vers la scène ; l’ovni est sélectionné) :

Et la même scène affichée en perspective :

Le fichier d’origine, avec un ovni, est téléchargeable ici :

création de l’autre ovni

On commence par repérer, dans la fenêtre « info », le bouton « duplicate » (n’est visible que si l’ovni est sélectionné) :

On clique évidemment sur ce bouton, et on bouge la souris pour bouger le second ovni ; puis on le place à sa position initale :

On le renomme (dans la fenêtre des propriétés) :

En cliquant sur le bouton « material » on constate qu’il est bleu :

On détache ce materiel et on en crée un nouveau, qui est rouge (couleur diffuse rouge, couleur spéculaire rose et algorithme « Phong ») :

Mais même avec une camera dirigée vers cet ovni, on ne le voit pas ; c’est parce que par défaut, la caméra ne voit que jusqu’à 100 mètres. Alors qu’on l’a placée sur les x négatifs, il faut donc agrandir son champ de vision :

Un rendu confirme que l’ovni rouge est en vue (et même menaçant, avec cette courte distance focale)

Le fichier complet, avec les deux ovnis placés à leur position initiale, peut servir de début à cette activité :

Conditions initiales

On doit ensuite mettre une des fenêtres sur « timeline » :

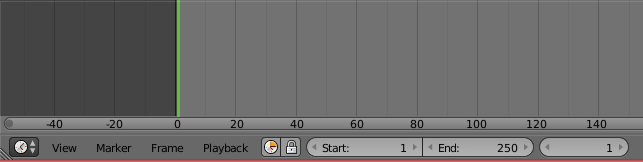
On est face à un mini éditeur vidéo. On constate que le film est long de 250 « frames » (images). Or on peut faire deux calculs qui serviront pour la suite :

• L’ovni bleu allant à 5 mètres par seconde, il lui faudra 20 secondes pour parcourir les 100 mètres ;
• Par contre l’ovni rouge avançant à 8 mètres par seconde, il lui faudra 12,5 secondes pour parcourir les 100 mètres.

On doit donc, ou bien convertir ces durées en frames, ou bien, au contraire, adapter la vitesse de la vidéo à ce problème. On clique donc sur l’icône représentant un appareil photo pour voir les réglages de la caméra :

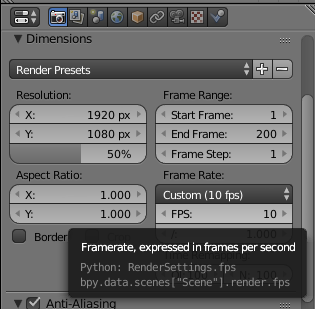
On met alors le « framerate » à 10 secondes, ce qui donne alors, en frames, les temps « clé » du film :

• frame 1, l’ovni bleu en x=0 et l’ovni rouge en x=100 ;
• frame 125, l’ovni rouge en x=0
• frame 200, l’ovni bleu en x=100

La durée totale du film est alors raccourcie, on n’a plus besoin que de 200 frames. Le réglage a été fait ci-dessus. Maintenant, dans la « timeline », on peut choisir une « frame » et se placer dans l’animation :

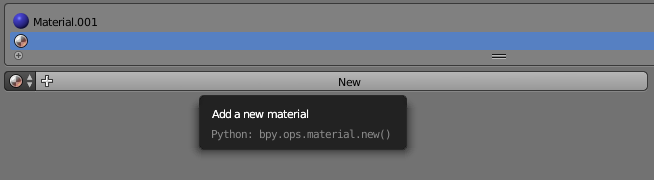
Sur la frame 1, l’ovni bleu doit être positionné en x=0 (il l’est déjà) et sa position doit être enregistrée par une « key » (clé). Pour se faire, après avoir sélectionné l’ovni bleu, on appuie sur le bouton « i », ce qui affiche ce menu :

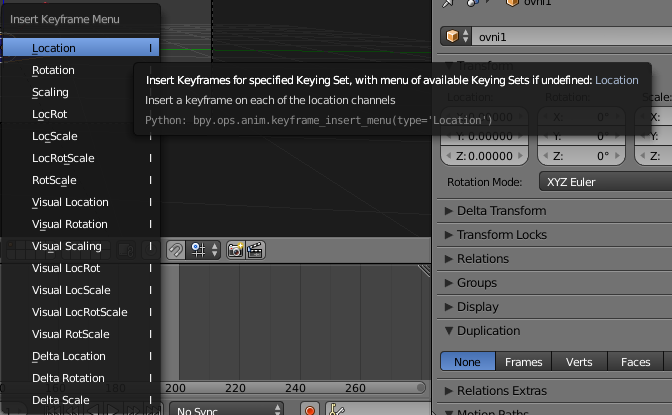
En cliquant sur « location », la position de l’ovni bleu est enregistrée. Ensuite on sélectionne l’ovni rouge et on enregistre pour lui aussi, une clé. On constate alors que dans la liste des objets, des flèches en zigzag sont apparues pour les deux ovnis ; elles signifient qu’ils sont maintenant animés :

Ensuite, on se positionne à la frame 125, on place l’ovni rouge en x=0, et on enregistre une clé. Puis on se place à la frame 200, et on place l’ovni bleu en x=100, et le scénario du film est terminé :

On peut lancer une animation pour tester :

Le rendu du film, placé en début de cet article, montre (quoique moins bien que l’animation) que lorsque l’ovni rouge est arrivé à la gare x=0, l’ovni bleu continue à se déplacer, puisqu’il n’est pas encore arrivé (il lui reste le trajet entre les frames 125 et 200).

Voici le fichier avec animation, qui permet le rendu (en cliquant sur « render animation ») :

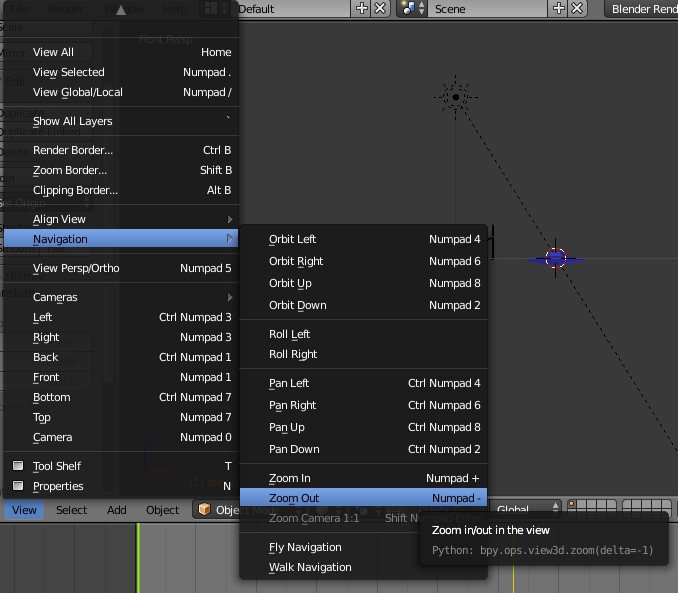
Le problème n’est pour autant pas résolu. On pourrait déjà améliorer la perspective, en rendant la caméra orthographique et en la positionnant en face du point x=50. On peut aussi sélectionner la vue de face, et alterner entre des « zoom out » et des « pan right » :

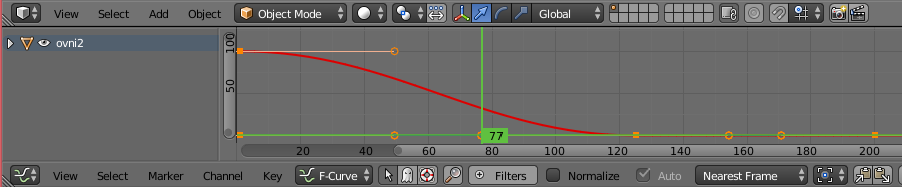
L’animation frame par frame montre alors que le croisement a lieu entre les frames 77 et 78 ce qui est peu précis mais indicatif : Il faut un peu moins de 8 secondes pour que les ovnis se croisent. Mais avant de chercher plus de précision, il y a un problème visible au début du film et à l’arrivée de l’ovni rouge : Au début l’ovni bleu met un peu de temps à démarrer et à son arrivée l’ovni rouge freine. Or il est bien connu que les ovnis ont des accélérations foudroyantes. Ce qui permet de modéliser les mouvements des ovnis par des fonctions affines, ce qui actuellement n’est pas le cas. Pour le vérifier, après avoir sélectionné l’ovni bleu, on remplace la « timeline » par un « graph editor », qui montre le caractère non linéaire du mouvement de l’ovni bleu :

Bien entendu, il en est de même pour l’ovni rouge :

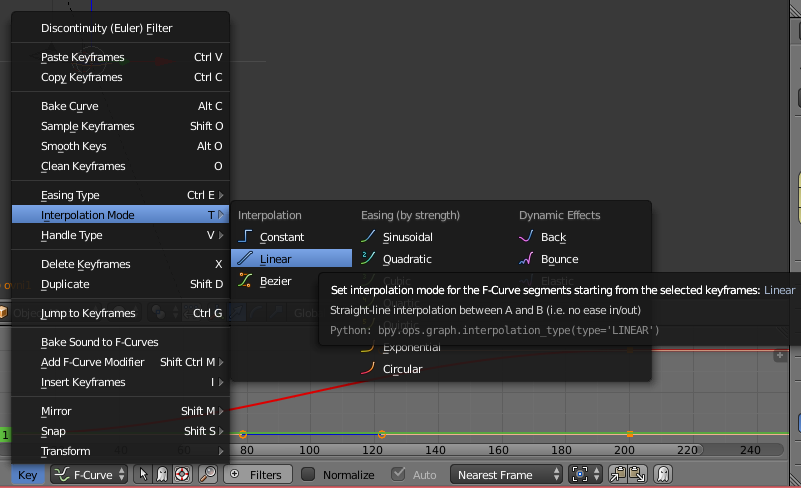
Cela est dû à ce que Blender, par défaut, interpole entre les clés d’animation, par courbes de Bezier. On choisit alors l’interpolation « linéaire » pour remettre les choses en ordre :

En faisant ce choix pour l’ovni bleu, on voit que cette fois-ci la courbe est droite :

Et en faisant pareil pour l’ovni rouge, la fonction est maintenant affine par morceaux (affine décroissante sur [0,125] et constante après) :

En sélectionnant simultanément les deux ovnis, on peut lire graphiquement la solution du problème (coordonnées du point d’intersection) :

Voici le fichier Blender avec vitesses constantes :

Et le film obtenu (on voit peu de différence avec la version non affine, sauf bien entendu au début et à l’arrivée de l’ovni rouge à 12,5 secondes, où les accélération et décélération sont plus brusques) :

Maintenant, il reste à trouver les valeurs exactes du temps et de la distance. Ceci se fait en exprimant les diagrammes horaires comme fonctions affines puis en résolvant une équation. Un logiciel de calcul formel peut aider.

• l’ovni bleu a un diagramme horaire linéaire (et pas seulement affine), on peut donc l’écrire x=5t puisque sa vitesse est 5 m/s.
• L’ovni rouge a une vitesse de -8 m/s puisqu’il va dans l’autre sens, et l’ordonnée à l’origine est 100 (position de départ). Il vérifie donc x=100-8t.

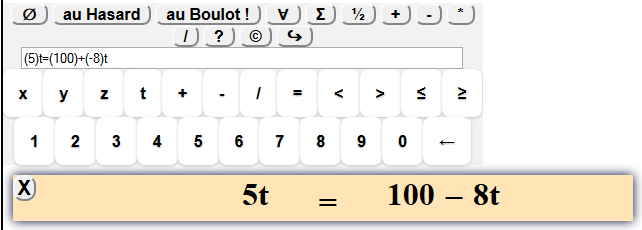
L’instant de croisement est donc la solution t de l’équation 5t=100-8t.

Résolution avec ekoarun

Effectivement, 100/13≈ 7,6923 et la distance 500/3 ≈ 38,46 : L’ovni bleu a parcouru 38,46 mètres au moment de la fusion avec l’ovni rouge.

Les diagrammes horaires dans un contexte classique

En fait, un diagramme horaire similaire à ceux vus ci-dessus enlève au paradoxe d’Achille et de la tortue son caractère paradoxal. Dans ce cas, les deux mobiles (Achille et la tortue) vont dans le même sens, mais à des vitesses différentes.

Le diagramme en toile d’araignée ci-dessous montre que, s’il y a une infinité de marches d’escalier, la longueur totale de l’escalier est finie, ce qui résout à sa façon le paradoxe de Zénon. La trajectoire d’Achille est en marron (Achille est bronzé à force de courir partout), celle de la tortue est verte (couleur de la tortue) et le trajet d’Achille tel que décrit par Zénon est en bleu. On voit la rapidité de convergence quelle que soit le « handicap » d’Achille (position initiale de la tortue, réglable en bougeant le point T) :

Comme le chemin de fer de La Réunion est du passé, il est difficile d’estimer un temps de croisement en regardant un vrai train. Alors Blender permet de modéliser les mouvements et même de représenter graphiquement les diagrammes horaires, pour aller de la modélisation à la solution du problème. C’est appréciable !

Pour les amateurs de train, une version plus traditionnelle peut être tentée à partir de ce fichier. Et la modélisation avec Blender peut être mise en œuvre en probabilité, comme par exemple avec une modélisation de dés qui tombent ou de planche de Galton...