Le cas de deux cercles inscrits égaux

J’avoue être arrivé un peu tard sur ce sujet (pendant les vacances de juillet 2009 alors que la revue a été publiée en avril) aussi n’ai-je pas cherché à résoudre cette partie, mes deux collègues Dominique Tournès et Jean-Marc Breslaw l’ayant fait bien avant comme exercice d’entraînement. Plus précisément ils ont répondu à la question de la revue :

On partage le triangle ABC en deux triangles ABM et AMB ayant leurs cercles inscrits de même rayon r. Calculer la valeur de AM en fonction des longueurs a, b et c des côtés du triangle.

On trouve $4AM^2 = (b+c-a)(b+c+a)$, ou encore $\boxed{AM = \frac{\sqrt{(b+c)^2-a^2}}{2}}\,.$

Preuve proposée par Jean-Marc Breslaw

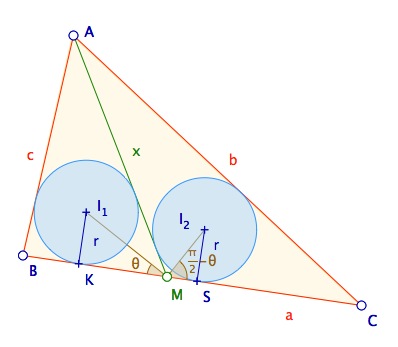
Avec les notations usuelles ci-dessus, rappelons que $KM =\frac{x+BM-c}{2}$ et $SM =\frac{x+CM-b}{2}$.

Alors $\tan(\theta) =\frac{2r}{x+BM-c}$ et $\frac{1}{\tan(\theta)}=\frac{2r}{x+CM-b}$.

En sommant les inverses, on obtient $\frac{r}{\cos(\theta)\sin(\theta)}=\frac{2x+a-b-c}{2}$, ou :

$(1)\quad \frac{r}{\sin(\widehat{AMB})}=\frac{r}{\sin(\widehat{AMC})}=\frac{2x+a-b-c}{4}$.

D’autre part, en exprimant les aires des triangles AMB et AMC, on obtient $x.BM.\sin(\widehat{AMB})=r(c+x+BM)$ et $x.CM.\sin(\widehat{AMC})=r(b+x+CM)$, soit :

$(2)\quad \frac{r}{\sin(\widehat{AMB})}=\frac{x.BM}{x+BM+c}=\frac{x.CM}{x+CM+b}=\frac{x.a}{2x+a+b+c}$.

On déduit de (1) et (2) : $4ax = (2x+a+b+c)(2x+a-b-c)$, et donc $x = \frac{\sqrt{(b+c)^2-a^2}}{2}$ .

Une seconde preuve sera proposée par Dominique Tournès à l’onglet TCIEray qui va aussi calculer directement le rayon r du cercle en fonction de a, b et c et de n avec une fabuleuse expression à la clé.

Ayant obtenu cette valeur de AM, Il suffit de faire une figure pour s’apercevoir que sa simple utilisation ne répond pas aux contraintes d’une figure dynamique. Par contre, la valeur de AM permet d’exprimer M comme barycentre de B et C et donc de réaliser une figure dynamique correcte. Voici les étapes de cette recherche, regroupées en une seule figure :

<carmetal|doc=1450|largeur=679|hauteur=510>

(Parcourir les différents items de la figure ; les relations présentées seront utilisées plus loin.)

Le cas de trois cercles inscrits égaux - Relation entre les côtés

On peut appliquer ce qui précède aux parties d’un triangle partagé en trois triangles de cercles inscrits égaux. Du sommet A du triangle ABC, on trace les segments [AX] et [AY], de longueurs respectives x et y, tels que ABX, AXY et AYC aient des cercles inscrits égaux. On continue de noter c’ la longueur sur [BC] du côté de B : c’ = BX. On note b’ = YC et a’ = XY.

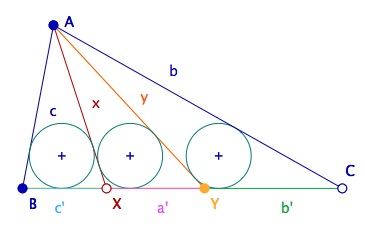
En appliquant les relations vues au dernier item de la figure précédente, aux deux triangles ABY et AXC qui ont tous les deux un partage en deux triangles de cercles inscrits de rayon r, on a tout de suite :

• X est barycentre de B $\left(\frac{x+y}{2x+c+y}\right)$, Y $\left(\frac{x+c}{2x+c+y}\right)$ ;
• Y est barycentre de X $\left(\frac{y+b}{2y+x+b}\right)$, C $\left(\frac{y+x}{2y+x+b}\right)$.

Ce qui donne, en exprimant X et Y comme barycentres de B et C :

• X est barycentre de B $\left(\frac{2y+x+b}{2x+2y+b+c}\right)$, C $\left(\frac{x+c}{2x+2y+b+c}\right)$ ;
• Y est barycentre de B $\left(\frac{y+b}{2x+2y+b+c}\right)$, C $\left(\frac{2x+y+c}{2x+2y+b+c}\right)$.

On en déduit aussitôt les valeurs de c’, a’, b’ en fonction de a, b, c, x et y :

$c’ = \frac{a(x+c)}{2x+c+y}$, $a’ = \frac{a(x+y)}{2x+c+y}$, $b’ = \frac{a(y+b)}{2x+c+y}$.

Ces calculs étant faits, même sans pouvoir encore calculer x et y, on peut déjà les vérifier sur une figure de travail.

Ouvrir la figure dynamique

En effet, on peut commencer par faire une figure avec deux cercles inscrits égaux, et ajouter, par construction, un troisième cercle inscrit de même rayon à droite. La figure n’est pas dynamique dans le sens où ce n’est pas ABC qui est dynamiquement découpé, mais en fait ABY. Le point C est construit par la suite, mais cette figure permet à la fois de vérifier les calculs et de conduire quelques analyses.
Elle est présentée ici de manière plus complète, car elle contient des vérifications des calculs suivants.

<carmetal|doc=1451|largeur=736|hauteur=577>

Une fois les coordonnées barycentriques de X et Y calculées, on peut revenir à l’expression initiale de x en fonction des côtés de ABY et à celle de y en fonction des côtés de AXC. On a, toujours en appliquant la relation dans le cas des deux cercles :

$i)\quad 4x^2 = (c+y-a+b’)(c+y+a-b’)$ ;
$ii)\quad 4y^2 = (x+b-a+c’)(x+b+a-c’)$.

En utilisant les expressions de b’ et c’, on arrive à un système en (x, y) du troisième degré :

$(1)\quad (x+b-2y)(2x+2y+b+c)^2 = a^2(x+b+2y)$ ;
$(2)\quad (y+c-2x)(2x+2y+b+c)^2 = a^2(y+c+2x)$.

En faisant le quotient des deux, on a une relation du second degré entre x et y : $x^2- y^2 + bx -cy = 0$, soit encore :

$(3)\quad x(x+b) = y(y+c)$.

Cette dernière relation permet de calculer y facilement dès que l’on a trouvé l’expression de x.

On peut revenir à la figure précédente et constater que ces relations sont bien vérifiées.

Égalité des cercles inscrits suivants - Initialisation de la récurrence

Il s’agit maintenant de montrer que, dans l’hypothèse du partage de ABC en trois triangles de cercles inscrits égaux, les cercles inscrits des triangles regroupés par deux, ici ABY et AXC, sont encore égaux.

Pour cela on peut remarquer que, dans le cas du partage du triangle ABC en deux triangles de cercles inscrit égaux de rayon r, en notant encore R le rayon du cercle inscrit du triangle initial, on a :

$\frac{R}{r}=1+\frac{\sqrt{(b+c)^2-a^2}}{a+b+c} =1+ \frac{2m}{a+b+c}$.

Notons alors $R_x$ le rayon du cercle inscrit à ABY, partagé par le segment de longueur x et $R_y$ celui du cercle inscrit à AXC partagé par le côté de longueur y. On a :

$\frac{R_x}{r} = 1+\frac{2x}{c+y+c’+a’}\ $ et $\ \frac{R_y}{r} = 1+\frac{2y}{x+b+a’+b’}$.

Ainsi les deux cercles auront même rayon si et seulement si $\frac{x}{y} = \frac{c+y+c’+a’}{x+b+a’+b’}$.

En notant $D = 2x+2y+b+c$ le dénominateur qui intervient dans l’expression des trois longueurs a’, b’, c’, on peut écrire :

$\frac{c+y+c’+a’}{x+b+a’+b’} =\frac{D(c+y)+a(2x+y+c)}{D(x+b)+a(2y+x+b)}=\frac{(y+c)(D+a)+2ax}{(x+b)(D+a)+2ay} \quad (a).$

Or $(y+c)(D+a)+2ax =(y+c)\left((D+a)+\frac{2ax}{y+c}\right)$ et
$(x+b)(D+a)+2ay =(x+b)\left((D+a)+\frac{2ay}{x+b}\right)$.

Or on a vu — par (3) — que $\frac{y}{x+b} = \frac{x}{y+c}$, donc le quotient (a) est égal à $\frac{y+c}{x+b}$, c’est-à-dire à $\frac{x}{y}$, toujours par (3).

En reprenant les calculs en détail, on voit que l’égalité (3) est équivalente à l’égalité des rayons des cercles inscrits des triangles de partage pris par deux.

Là encore on peut se reporter à l’item 5 de la figure de travail précédente pour en voir une illustration.

Cas de quatre cercles - Hérédité de la récurrence

Dans cette partie, nous allons détailler les relations entre les différentes variables dans le cas de quatre cercles en mettant en évidence la généralité des calculs : ce passage de trois à quatre cercles contient exactement les mêmes calculs que le passage de n à n + 1 cercles, mais cela sera abordé plus en détail dans l’onglet suivant.

Les preuves sont rassemblées en blocs. Cliquer sur les blocs pour lire les détails et sur le bloc de la figure pour une illustration.

On reprend la figure de base (la figure suivante illustre les vérifications possibles des calculs) : le triangle ABC est désormais partagé en quatre triangles dont les sommets sur [BC] sont successivement X, Y et Z. Le premier triangle est ABX et le quatrième AZC. On notera encore x, y, z les longueurs des segments [AX], [AY], [AZ], puis c’ = BX, x’ = XY, y’ = YZ et b’ = ZC.

Calculs barycentriques de X, Y et Z

Calculs barycentriques de X, Y et Z

On applique les résultats obtenus pour le cas de trois cercles aux deux triangles ABZ et AXC.

Dans le triangle ABZ, on peut écrire :

• X est barycentre de B : $\frac{2y+x+z}{2x+2y+c+z}$ et de Z : $\frac{x+c}{2x+2y+c+z}$ ;
• Y est barycentre de B : $\frac{y+z}{2x+2y+c+z}$ et de Z : $\frac{2x+y+c}{2x+2y+c+z}$.

Dans le triangle AXC, on a aussi

• Y est barycentre de X : $\frac{2z+y+b}{2y+2z+x+b}$ et de C : $\frac{y+x}{2y+2z+x+b}$ ;
• Z est barycentre de X : $\frac{z+b}{2y+2z+x+b}$ et de C : $\frac{2y+z+x}{2y+2z+x+b}$.

On remarquera que le numérateur du coefficient de B pour X dans le premier triangle est le même que celui de C pour Z dans le second triangle, ce qui permet la simplification "attendue" quand on cherche les coefficients barycentriques de X et Y dans le repère (B, C). Il vient alors :

• X est barycentre de B : $\frac{x+2y+2z+b}{2(x+y+z)+b+c}$ et de C : $\frac{x+c}{2(x+y+z)+b+c}$ ;
• Z est barycentre de B : $\frac{z+b}{2(x+y+z)+b+c}$ et de C : $\frac{z+2y+2x+c}{2(x+y+z)+b+c}$.

En regardant les expressions barycentriques pour deux cercles, puis pour trois cercles, on voit s’installer une stabilité qui permet de poser une relation de récurrence pour les points extrêmes du partage : les expressions du numérateur pour les deux points extrêmes ne changent pas (respectivement x + c et z + b) et la remarque précédente sera toujours vraie puisque l’on prendra toujours les deux triangles composés de n - 1 triangles de partage dans le cas d’un partage en n triangles.
L’expression du dénominateur est claire et la même remarque assure son hérédité.

En pratique, ces deux calculs suffisent pour montrer aussi l’égalité des rayons des deux derniers cercles inscrits, mais poursuivons quand même les calculs pour les points intermédiaires, ici le point Y et les longueurs x’ et y’.

En utilisant l’expression de Z dans (B, C) dans l’expression de Y dans (B, Z), il vient :

• Y est barycentre de B : $\frac{y+2z+b}{2(x+y+z)+b+c}$ et de C : $\frac{y+2x+c}{2(x+y+z)+b+c}$.

Il fallait faire ce calcul pour pouvoir conjecturer la relation de récurrence pour les points intermédiaires. Ces calculs donnent alors pour les longueurs

$c’=a\frac{x+c}{2(x+y+z)+b+c}$ , $x’=a\frac{x+y}{2(x+y+z)+b+c}$, $y’=a\frac{y+z}{2(x+y+z)+b+c}$ et $b’=a\frac{z+b}{2(x+y+z)+b+c}$.

Figure dynamique d’illustration pour le cas n = 4

Figure d’illustration pour le cas n = 4

<carmetal|doc=1455|largeur=719|hauteur=515>

Égalité des rayons des deux derniers cercles

Égalité des rayons des deux derniers cercles

Comme détaillé dans l’item 5 de la figure d’illustration du bloc dépliable ci-dessus, quand on dispose de quatre (ou plus) cercles inscrits égaux, on a automatiquement l’égalité des cercles du rang au dessus. Dans tous les cas, il reste à vérifier l’égalité des deux derniers cercles, avant le cercle inscrit à ABC.

Pour cela reprenons l’argument présenté dans la figure du paragraphe sur le partage en deux : le rapport h/r, pour une même hauteur h issue de A et un même rayon r, s’exprime de deux façons dans chacun des triangles. On cherche à égaliser ces deux valeurs.

Dans le cas qui nous occupe, le rapport $\frac{h}{R_1}$ du triangle ABZ vaut $\frac{c+z}{c’+x’+y’}$ et le rapport $\frac{h}{R_2}$ du triangle AXC vaut $\frac{x+b}{x’+y’+b’}$.

Les deux rayons sont égaux ssi ces rapports le sont et donc ssi on a

$\frac{c’+x’+y’}{x’+y’+b’}$ = $\frac{c+z}{x+b}.$

Là encore, on peut sentir le caractère générique de la situation puisque l’on traitera toujours des deux grand triangles d’ordre n - 1 dans un partage d’ordre n, et que les côtés extrêmes c’ et b’ ont toujours la même expression en fonction des données du problème.

Si une relation générale — donc ici de récurrence — permet de montrer cette égalité, alors cette preuve pour le cas n = 4 vaudra pour les cas pour n > 4. Démontrer le TCIE revient à chercher cette relation. Mais en fait, pour n = 4, la situation est encore trop élémentaire pour qu’on perçoive véritablement cette relation. Elle est bien sûr une généralisation de la relation (3) qui a déjà permis de résoudre l’égalité des "deux derniers cercles" dans le cas n = 3.

Actualisons quelque peu cette relation pour tenter de la généraliser :

Dans le cas de trois cercles on a la relation $x^2-y^2=yc-bx$. Cette relation s’écrit aussi $x(x+b) = y(y+c)$. Nous avons déjà noté qu’elle est équivalente à l’égalité des rayons de rang supérieur pour le cas n = 3. Regardons ce qu’elle devient dans le cas de quatre cercles :

• Dans le triangle ABZ, la relation s’écrit : $x^2-y^2 = yc-xz$.
• Dans le triangle AXC, elle devient : $y^2-z^2 = zx-yb$.

Soit en sommant : $x^2-z^2 = y(c-b)$, relation élémentaire, mais bien trop particulière — due à la position médiane de y qui est à la fois le second segment en partant de B et le $(n-2)^{ième}$ en partant de C. Cette particularité ne doit toutefois pas masquer la généralité du procédé comme nous le verrons dans la preuve par récurrence générale.

L’expression (3) sous forme de produit va nous être utile aussi. Elle peut s’écrire, dans les deux triangles de rang 3 : $x(x+z)=y(y+c)$ et $y(y+b)=z(z+x)$, soit encore, après simplification, $\frac{x}{z}= \frac{y+c}{y+b}$, là encore expression que l’on saura étendre au cas général. Pour ce qui nous intéresse, on a donc $x(y+b) =z(y+c)$.

Reste à voir que cette relation donne bien l’égalité des rapports. En exprimant les côtés en fonction de x, y, et z (considérés comme les deux côtés des triangles de rang n - 1, et en simplifiant par a, on cherche à montrer l’égalité :

$\frac{2x+2y+z+c}{x+2y+2z+b} = \frac{c+z}{x+b}$

Soit encore à montrer la nullité de l’expression (E) : $(2x+2y+z+c)x+b)- (x+2y+2z+b)(c+z)$.

Après simplification cette expression s’écrit : $x^2+xy+b(x+y)-z^2-yz-c(y+z).$

Soit $\left(x^2-z^2+(b-c)y\right)+\left((xy+bx)-(yz+cy)\right).$

La première parenthèse est nulle de par la relation (3) du second degré entre x et z, la seconde parenthèse est nulle de par la version "produit" de cette même relation étendue.

Ainsi les rayons des cercles inscrits des triangles de rang 3 (i. e. formés de trois petits triangles) sont égaux, ce qui achève la démonstration du théorème des cercles inscrits égaux, pour le rang 4.

Là encore on voit que la relation $x(y+b) =z(y+c)$, une fois correctement indicée, est équivalente à l’égalité des rayons des cercles inscrits des triangles de rang 3 dans un triangle de rang 4, inclus dans un partage plus général.

Complément sur la construction de TCIE4

Complément sur la construction de TCIE4

Le rayon des cercles inscrits d’un partage en 2 ne dépend pas que du rayon du cercle inscrit initial.

C’est une évidence depuis le calcul de Dominique Tournès, bien entendu, mais cela invite à réflexion quant à la double application du partage en 2 pour un partage en 4. Ici une figure d’archive (i. e. d’avant le calcul) pour illustrer que deux triangles ayant des cercles inscrits égaux ne produisent pas des partages en deux de cercles ayant même rayon.

<carmetal|doc=1456|largeur=641|hauteur=451>

La démonstration par récurrence

Cette partie contient aussi une figure de travail sur un partage en 7 et en 8 qui permet d’observer la validation des différentes étapes de la récurrence

La première partie de la preuve, sur la barycentration des points de partage, est une réécriture indicée de la partie précédente. Mais la particularité du cas n = 4 cache quelque peu la relation qui permet de montrer l’égalité des derniers rayons de cercles. C’est ce que nous allons préciser dans une seconde partie.

On considère donc un triangle ABC, de côtés respectifs a = BC, b = AC et c = AB que l’on veut partager en n triangles $AM_{k-1}M_k$ pour $1\leq k \leq n$, ayant tous même rayon de cercle inscrit de rayon $r=r_{n,1}$, avec $M_0$ = $B$ et $M_n$ = $C$.

On notera $x_k$ la longueur du segment [$AM_k$] pour $1\leq k \leq n-1$ car on conservera la notation b et c respectivement pour $x_n$ et $x_0$.
On appellera triangle de rang p un triangle formé de p de ces $AM_{k-1}M_k$ triangles contigus. Le triangle ABC est le seul de rang n. Dans la récurrence, on s’intéressera plus particulièrement aux deux triangles de rang n - 1, $ABM_{n-1}$ et $AM_1C$.

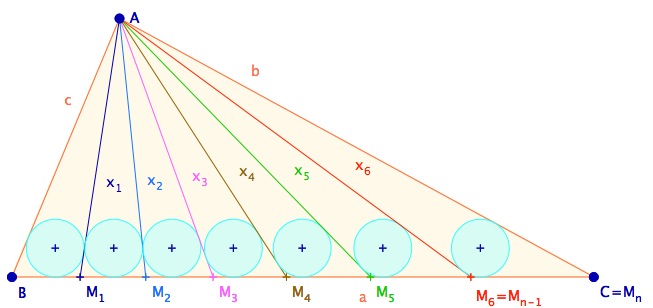
Le théorème des cercles inscrits égaux (TCIE) dit que si les triangles de rang 1 ont des cercles inscrits égaux (de rayon $r_{n,1}$), alors les triangles de rang supérieur k ont aussi leurs cercles inscrits égaux $r_{n,k}$. Le cercle inscrit à ABC étant le cercle de rayon $r_{n,n}$ que l’on a noté R au début de cet article et dans certaines figures.

Les paragraphes précédents ont montré ce résultat d’abord pour n = 3 en montrant directement l’égalité des rayons $r_{3,2}$. Pour n = 4, on a vu que l’utilisation du résultat pour n = 3 permet de traiter directement le cas des triangles de rang 2 (les cercles de rayon $r_{4,2}$). Il a fallu à nouveau montrer le résultat pour les deux cercles des triangles de rang 3. On l’a fait avec un regard vers la récurrence.

La transitivité de l’égalité des rayons $r_{n,k}$ des cercles des triangles de rang k, quand il y a au moins trois cercles à ce rang-là, assure dans le cas n, le théorème étant supposé vrai au rang n - 1, l’égalité des rayons des cercles inscrits du rang n - 2 (3 cercles de rayon $r_{n,n-2}$) au rang 1 (les n cercles de rayon $r_{n,1}$, égaux eux par hypothèse). La seule chose à montrer est donc l’égalité au rang n - 1 des deux cercles inscrits dans $ABM_{n-1}$ et $AM_1C$.

La démonstration est organisée en trois parties, répartie sur trois blocs dépliables et un bloc pour une figure d’illustration :

Calcul explicite des rayons des cercles inscrits des différents rangs et seconde preuve du théorème

Jean-Marc Breslaw ayant attiré mon attention sur le problème posé par la revue Tangente, j’ai tout d’abord, comme lui, pris plaisir à calculer AM en fonction de a, b et c. Ma preuve est essentiellement la même que celle de mon collègue, reproduite plus haut dans l’onglet TCIE2, si ce n’est que je pars d’une autre expression, sans doute moins connue, du rayon du cercle inscrit dans un triangle. Le lecteur curieux pourra consulter ce second calcul de AM dans le bloc dépliant ci-dessous.

Les investigations fascinantes d’Yves Martin autour de ce Sangaku m’ont ensuite donné envie de chercher une expression explicite du rayon $r_{n,1}$ des cercles inscrits égaux, dans le cas général où l’on veut en construire n sur le côté [BC] du triangle. Une telle expression me semblait indispensable pour dépasser les difficultés rencontrées dans la construction dynamique des figures. Je vais décrire ci-dessous les calculs exploratoires que j’ai effectués pour $n \leq 4$ et les résultats généraux qui en ont découlé.

Rappelons les notations introduites par Yves Martin : on partage un triangle ABC en n triangles $AM_{i-1}M_i$, avec $1\leq i\leq n$, $M_0 =B$ et $M_n=C$, de telle façon que tous ces triangles aient leurs cercles inscrits de même rayon $r_{n,1}$. Pour $2 \leq k \leq n-1$ et $0 \leq i \leq n-k$, on note $r_{n,k,i}$ le rayon du cercle inscrit au triangle $AM_{i}M_{i+k}$. Le but est de trouver des formules explicites pour les $r_{n,1}$ et les $r_{n,k,i}$ en fonction des côtés a, b et c du triangle.

Rappelons également les relations classiques dont nous aurons besoin, pour un triangle ABC, entre son demi-périmètre p, son aire S et le rayon r de son cercle inscrit :

$p=\dfrac{a+b+c}{2}$ ; $\quad S=\sqrt{p(p-a)(p-b)(p-c)}$ ; $\quad r=\dfrac{S}{p}$.

Calculs exploratoires pour n = 2, 3 et 4

Calcul de $r_{2,1}$

Dans le cas de deux cercles, écrivons que l’aire du triangle ABC est la somme des aires des triangles $ABM_{1}$ et $AM_{1}C$ :

$S=\dfrac{r_{2,1}}{2} (AB+BM_{1}+AM_{1}) +\dfrac{r_{2,1}}{2} (AM_{1}+M_{1}C+CA),$

soit encore : $S=\dfrac{r_{2,1}}{2} (a+b+c+2AM_{1})=r_{2,1}(p+AM_{1})$.

Sachant que $AM_{1}=\dfrac{\sqrt{(b+c)^2-a^2}}{2}=\sqrt{p(p-a)}$, il vient :

$r_{2,1}=\dfrac{S}{p+p^{1/2}(p-a)^{1/2}}=\dfrac{S}{p^{1/2}(p^{1/2}+(p-a)^{1/2})}=\dfrac{S}{p^{1/2}}\dfrac{p^{1/2}-(p-a)^{1/2}}{a},$ soit enfin :

Calcul de $r_{3,1}$ et des $r_{3,k,i}$

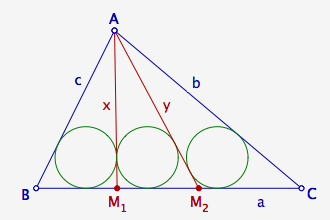
Pour trois cercles, écrivons de même que l’aire du triangle ABC est la somme des aires des triangles $ABM_{1}$, $AM_{1}M_{2}$ et $AM_{2}C$ :

$S=\frac{r_{3,1}}{2}(AB+BM_{1}+AM_{1}+AM_{1}+M_{1}M_{2}+AM_{2}+AM_{2}+M_{2}C+AC)=r_{3,1}(p+AM_{1}+AM_{2}),$

d’où : $r_{3,1}=\dfrac{S}{p+AM_{1}+AM_{2}}\,.$

La difficulté est ici de calculer $x = AM_{1}$ et $y = AM_{2}$. Comme Yves Martin l’a montré dans l’onglet TCIE3, x et y vérifient le système :

$(1)\quad (x+b-2y)(2x+2y+b+c)^2 = a^2(x+b+2y)$ ;
$(2)\quad (y+c-2x)(2x+2y+b+c)^2 = a^2(y+c+2x)$.

Le calcul explicite de x et de y est extrêmement compliqué, mais, en fait, on n’a pas besoin de les connaître individuellement, puisque seule la somme $AM_{1} + AM_{2}$ intervient dans l’expression du rayon $r_{3,1}$. D’où l’idée de chercher une équation d’inconnue s = x + y, équation qui s’obtient directement en ajoutant (1) et (2) :

$(b+c-s)(2s+b+c)^2=a^2(3s+b+c),$

ou encore : $(2p-a-s)(2s+2p-a)^2=a^2(3s+2p-a),$

soit enfin : $s^3-3p(p-a)s-p(p-a)(2p-a)=0.$

Cette équation réduite du troisième degré a une forme plutôt sympathique. Elle admet une racine réelle et deux racines imaginaires conjuguées. En appliquant la formule de Cardan ou en s’aidant d’un logiciel de calcul formel, on trouve $s=p^{2/3}(p-a)^{1/3}+p^{1/3}(p-a)^{2/3}$ pour la racine réelle, ce qui permet d’exprimer finalement le rayon des trois cercles inscrits :

Considérons maintenant les configurations de deux cercles inscrits égaux dans les triangles $ABM_{2}$ et $AM_{1}C$. Notons S’, r’, p’ et a’ (resp. S’’, r’’, p’’ et a’’) l’aire, le rayon du cercle inscrit, le demi-périmètre et la base du triangle $ABM_{2}$ (resp. $AM_{1}C$). En appliquant le résultat vu plus haut pour deux cercles, le rayon $r_{3,1}$ peut s’exprimer de deux façons :

$r_{3,1}=\dfrac{S’}{a’} \left[ 1- \left( 1-\dfrac{a’}{p’} \right)^{1/2} \right] =\dfrac{S’’}{a’’} \left[ 1- \left( 1-\dfrac{a’’}{p’’} \right)^{1/2} \right].$

Une remarque cruciale, que nous utiliserons systématiquement dans la suite, est que tous les triangles de sommet A ayant même hauteur, leurs aires sont proportionnelles à leurs bases.

Ici, $\dfrac{S’}{a’}=\dfrac{S’’}{a’’}$, d’où $\dfrac{a’}{p’}=\dfrac{a’’}{p’’}$. Par suite, $\dfrac{S’}{p’}=\dfrac{S’’}{p’’}$, c’est-à-dire $r_{3,2,0}=r_{3,2,1}$.

De la relation $r_{3,1}=\dfrac{S}{a} \left[ 1- \left( 1- \dfrac{a}{p} \right)^{1/3} \right]= \dfrac{S’}{a’} \left[ 1- \left( 1-\dfrac{a’}{p’} \right)^{1/2} \right],$ compte tenu de $\dfrac{S}{a}=\dfrac{S’}{a’}$, on tire $1-\dfrac{a’}{p’}=\left( 1- \dfrac{a}{p} \right)^{2/3}$, d’où :

$r_{3,2,0}=r_{3,2,1}=\dfrac{S’}{p’}=\dfrac{S’}{a’}\dfrac{a’}{p’}=\dfrac{S}{a}\left[ 1- \left( 1- \dfrac{a}{p} \right)^{2/3} \right].$

Calcul de $r_{4,1}$ et des $r_{4,k,i}$

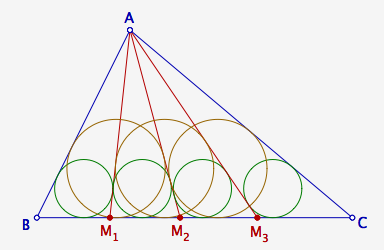
Dans le cas de quatre cercles, nous avions aussi, dans un premier temps, calculé péniblement par radicaux la somme $AM_{1}+AM_{2}+AM_{3}$. Nous allons suivre ici une approche plus simple, exploitant mieux le résultat déjà acquis pour deux cercles.

Sur la figure, il apparaît tout d’abord trois configurations de deux cercles inscrits égaux, dans les triangles $ABM_{2}$, $AM_{1}M_{3}$ et $AM_{2}C$. Notons S’, r’, p’ et a’ (resp. S’’, r’’, p’’ et a’’, resp. S’’’, r’’’, p’’’ et a’’’) l’aire, le rayon du cercle inscrit, le demi-périmètre et la base du triangle $ABM_{2}$ (resp. $AM_{1}M_{3}$, resp. $AM_{2}C$). Le rayon $r_{4,1}$ peut ainsi s’exprimer de trois façons :

$r_{4,1}=\dfrac{S’}{a’} \left[ 1- \left( 1-\dfrac{a’}{p’} \right)^{1/2} \right] =\dfrac{S’’}{a’’} \left[ 1- \left( 1-\dfrac{a’’}{p’’} \right)^{1/2} \right] = \dfrac{S’’’}{a’’’} \left[ 1- \left( 1-\dfrac{a’’’}{p’’} \right)^{1/2} \right].$

Comme $\dfrac{S’}{a’}=\dfrac{S’’}{a’’}=\dfrac{S’’’}{a’’’}$, il vient $\dfrac{a’}{p’}=\dfrac{a’’}{p’’}=\dfrac{a’’’}{p’’’}$ et, par suite, $\dfrac{S’}{p’}=\dfrac{S’’}{p’’}=\dfrac{S’’’}{p’’’}$, c’est-à-dire $r_{4,2,0}=r_{4,2,1}=r_{4,2,2}$.

Les trois cercles inscrits de rang 2 ont donc même rayon. En particulier, le triangle ABC, partagé en $ABM_{2}$ et $AM_{2}C$, est une nouvelle configuration de deux cercles inscrits égaux, ce qui permet d’écrire :

$r_{4,2,0}=r_{4,2,1}=r_{4,2,2}= \dfrac{S}{a} \left[ 1- \left( 1-\dfrac{a}{p} \right)^{1/2} \right].$

Des relations $r_{4,2,0}= \dfrac{S’}{p’}=\dfrac{S’}{a’}\dfrac{a’}{p’}=\dfrac{S}{a}\dfrac{a’}{p’}=\dfrac{S}{a} \left[ 1- \left( 1-\dfrac{a}{p} \right)^{1/2} \right],$ on tire $1-\dfrac{a’}{p’}=\left( 1- \dfrac{a}{p} \right)^{1/2}$, ce qui, compte tenu de $\dfrac{S’}{a’}=\dfrac{S}{a}$, donne finalement :

Il nous reste à étudier les cercles de niveau 3, ceux qui sont inscrits dans les triangles $ABM_{3}$ et $AM_{1}C$. Notons S’, r’, p’ et a’ (resp. S’’, r’’, p’’ et a’’) les quantités qui leur sont associées. En réinvestissant le résultat trouvé pour trois cercles, il vient :

$r_{4,1}=\dfrac{S’}{a’} \left[ 1- \left( 1-\dfrac{a’}{p’} \right)^{1/3} \right] =\dfrac{S’’}{a’’} \left[ 1- \left( 1-\dfrac{a’’}{p’’} \right)^{1/3} \right],$

d’où $\dfrac{a’}{p’}=\dfrac{a’’}{p’’}$ et, par suite, $\dfrac{S’}{p’}=\dfrac{S’}{a’}\dfrac{a’}{p’}=\dfrac{S’’}{a’’}\dfrac{a’’}{p’’}=\dfrac{S’’}{p’’}$, c’est-à-dire $r_{4,3,0}=r_{4,3,1}$.

Enfin, de l’égalité $r_{4,1}=\dfrac{S}{a} \left[ 1- \left( 1-\dfrac{a}{p} \right)^{1/4} \right]=\dfrac{S’}{a’} \left[ 1- \left( 1-\dfrac{a’}{p’} \right)^{1/3} \right]$, on tire $\left( 1- \dfrac{a’}{p’} \right)=\left( 1-\dfrac{a}{p} \right)^{3/4},$ d’où finalement :

$r_{4,3,0}=r_{4,3,1}=\dfrac{S’}{p’}=\dfrac{S’}{a’}\dfrac{a’}{p’}=\dfrac{S}{a} \left[ 1- \left( 1-\dfrac{a}{p} \right)^{3/4} \right].$

Conjectures pour les $r_{n,1}$ et les $r_{n,k,i}$

Ainsi, pour n = 2, n = 3 et n = 4, nous avons calculé les rayons de tous les cercles inscrits des différents rangs et nous avons constaté que le théorème des cercles inscrits égaux était vrai. Les résultats obtenus nous ont fait considérer comme des plus plausibles les conjectures suivantes :

La suite de l’onglet va être consacrée à la démonstration de ces formules.

Démonstration de la formule pour les cercles inscrits égaux du premier rang

Pour n = 2 et n = 3 (et aussi pour n = 4, mais cela est inutile pour initialiser la récurrence qui va suivre), nous avons établi directement la formule :

Nous allons maintenant démontrer par récurrence qu’elle est vraie pour tout n. Considérons donc un entier $n \geq 4$ et supposons que la formule soit vraie pour n - 2 et pour n - 1.

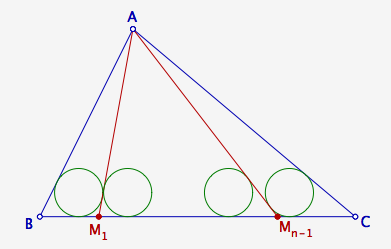
Nous allons travailler avec les triangles $ABM_{n-1}$ et $AM_{1}C$, qui contiennent $n-1$ cercles inscrits égaux, ainsi qu’avec le triangle $AM_{1}M_{n-1}$, qui en contient $n-2$. Notons $S_{1}$, $p_{1}$ et $a_{1}$ (resp. $S_{2}$, $p_{2}$ et $a_{2}$, resp. $S_{3}$, $p_{3}$ et $a_{3}$) l’aire, le demi-périmètre et la base du triangle $ABM_{n-1}$ (resp. $AM_{1}C$, resp. $AM_{1}M_{n-1}$).

Remarquons que :

1) $S_{1}+S_{2}-S_{3}=S$ ;

2) $a_{1}+a_{2}-a_{3}=BM_{n-1}+M_{1}C-M_{1}M_{n-1}=a$ ;

3) $p_{1}+p_{2}-p_{3}=\frac{1}{2}(c+a_{1}+AM_{n-1}+AM_{1}+a_{2}+b-AM_{1}-a_{3}-AM_{n-1})=p.$

En appliquant l’hypothèse de récurrence dans ces trois triangles, on obtient :

$r_{n,1}=\dfrac{S_{1}}{a_{1}} \left[1-\left( 1-\dfrac{a_{1}}{p_{1}} \right)^{1/(n-1)} \right]=\dfrac{S_{2}}{a_{2}} \left[1-\left( 1-\dfrac{a_{2}}{p_{2}} \right)^{1/(n-1)} \right]=\dfrac{S_{3}}{a_{3}} \left[1-\left( 1-\dfrac{a_{3}}{p_{3}} \right)^{1/(n-2)} \right].$

Comme $\dfrac{S_{1}}{a_{1}}=\dfrac{S_{2}}{a_{2}}=\dfrac{S_{3}}{a_{3}}=\dfrac{S}{a}$, on en déduit que :

$\left( 1-\dfrac{a_{1}}{p_{1}} \right)^{1/(n-1)}=\left( 1-\dfrac{a_{2}}{p_{2}} \right)^{1/(n-1)}=\left( 1-\dfrac{a_{3}}{p_{3}} \right)^{1/(n-2)}= 1-\dfrac{a\,r_{n,1}}{S}.$

Pour alléger les écritures, on posera à partir d’ici :

Dans le triangle $ABM_{n-1}$, on peut écrire, toujours d’après l’hypothèse de récurrence :

$p_{1}+\displaystyle{\sum_{k=1}^{n-2}AM_{k}}=p_{1}+\displaystyle{\sum_{k=1}^{n-2}p_{1}^{(n-1-k)/(n-1)}(p_{1}-a)^{k/(n-1)}}=p_{1}+p_{1}\displaystyle{\sum_{k=1}^{n-2} \left( 1- \dfrac{a_{1}}{p_{1}} \right)^{k/(n-1)}}$

$\quad \quad =p_{1}\displaystyle{\sum_{k=0}^{n-2}q^{k}}=p_{1}\,\dfrac{1-q^{n-1}}{1-q}.$

De façon analogue, on a dans le triangle $AM_{1}C$ : $p_{2}+\displaystyle{\sum_{k=2}^{n-1}AM_{k}}=p_{2}\,\dfrac{1-q^{n-1}}{1-q},$

et dans le triangle $AM_{1}M_{n-1}$ : $p_{3}+\displaystyle{\sum_{k=2}^{n-2}AM_{k}}=p_{3}\,\dfrac{1-q^{n-2}}{1-q}.$

En combinant les trois égalités précédentes, il vient :

$p_{1}+\displaystyle{\sum_{k=1}^{n-2}AM_{k}}+p_{2}+\displaystyle{\sum_{k=2}^{n-1}AM_{k}}-p_{3}-\displaystyle{\sum_{k=2}^{n-2}AM_{k}}=(p_{1}+p_{2}-p_{3})\,\dfrac{1-q^{n-1}}{1-q}+p_{3} \left[ \dfrac{1-q^{n-1}}{1-q}-\dfrac{1-q^{n-2}}{1-q} \right],$

soit encore : $\quad \boxed{p+x=p\,\dfrac{1-q^{n-1}}{1-q} +p_{3}\,q^{n-2} \quad (1)}\,.$

Dans cette formule transitoire importante, il reste une seule quantité liée aux trois triangles auxiliaires que nous avons introduits, à savoir $p_{3}$. Notre objectif sera donc maintenant d’éliminer $p_{3}$ en le calculant en fonction des quantités associées au triangle ABC. Pour cela, nous utiliserons la relation établie par Yves Martin pour le calcul des bases des triangles du partage (voir onglet TCIEn) :

$M_{k-1}M_{k}=a\,\dfrac{AM_{k-1}+AM_{k}}{2\,\displaystyle{\sum_{i=1}^{n-1} AM_{i}}+b+c}=a\, \dfrac{AM_{k-1}+AM_{k}}{2x+2p-a}.$

En sommant les n - 2 bases centrales, on obtient :

$a_{3}=M_{1}M_{n-1}=\displaystyle{\sum_{k=2}^{n-1}M_{k-1}M_{k}}=\dfrac{a}{2x+2p-a} \left( \displaystyle{\sum_{k=1}^{n-2} AM_{k}}+\displaystyle{\sum_{k=2}^{n-1} AM_{k}} \right)$

$\quad \quad =\dfrac{a}{2x+2p-a} \left( 2\,\displaystyle{\sum_{k=1}^{n-1} AM_{k}}-AM_{1}- AM_{n-1} \right)=\dfrac{a(2x-2p_{3}+a_{3})}{2x+2p-a},$

soit : $a_{3}(2x+2p-a)=a(2x-2p_{3}+a_{3}),$ ou encore : $a_{3}(2x+2p-2a)=a(2x-2p_{3}),$

c’est-à-dire : $\quad \boxed{(x+p-a)\,a_{3}+a\,p_{3}=ax\quad(2)}\,.$

Par ailleurs, souvenons-nous que $r=\dfrac{S}{p+x}=\dfrac{S}{a} \left[ 1- \left( 1-\dfrac{a_{3}}{p_{3}}\right)^{1/(n-2)} \right],$

d’où l’on tire : $\left( 1-\dfrac{a_{3}}{p_{3}}\right)^{1/(n-2)}=1-\dfrac{a}{p+x},$

puis : $\quad \boxed{a_{3}=p_{3} \left[ 1- \left(1-\dfrac{a}{p+x}\right)^{n-2} \right] \quad (3)}\,.$

Le système linéaire (2) et (3) permet de calculer $a_{3}$ et $p_{3}$. En fait, on n’a besoin que de $p_{3}$, que l’on trouve facilement en reportant dans (2) la valeur de $a_{3}$ fournie par (3) :

$p_{3}=\dfrac{ax}{p+x} \dfrac{1}{1- \left(1-\dfrac{a}{p+x}\right)^{n-1}}\,.$

Comme $q=1-\dfrac{ar}{S}=1-\dfrac{a}{p+x}$, on a l’écriture plus simple : $\quad \boxed{p_{3}=x\, \dfrac{1-q}{1-q^{n-1}} \quad (4)}\,.$

Reportons cette valeur de $q_{3}$ dans la relation cruciale (1), que nous avons laissée en attente :

$p+x=p\,\dfrac{1-q^{n-1}}{1-q} +x\,q^{n-2}\dfrac{1-q}{1-q^{n-1}}$.

Tout est en place pour achever le calcul de x :

$x \left( 1 -q^{n-2}\dfrac{1-q}{1-q^{n-1}} \right) = p \left( \dfrac{1-q^{n-1}}{1-q} - 1 \right),$

ce qui donne : $x\, \dfrac{1-q^{n-2}}{1- q^{n-1}}= p\,q\, \dfrac{1-q^{n-2}}{1-q},$ d’où $x=p\,q\, \dfrac{1-q^{n-1}}{1-q}$

et enfin : $p+x=p \left( 1+ \dfrac{q-q^{n}}{1-q} \right)=p\, \dfrac{1-q^n}{1-q}.$

Il ne reste plus qu’à revenir progressivement aux notations initiales :

$r=\dfrac{S}{p+x}=\dfrac{S}{p}\, \dfrac{1- \left(1-\frac{ar}{S} \right)}{1- \left( 1- \frac{ar}{S} \right)^{n}}= \dfrac{ar}{p} \dfrac{1}{1- \left( 1- \frac{ar}{S} \right)^{n}}$.

En simplifiant par r, il vient : $1- \left( 1- \dfrac{ar}{S} \right)^{n}=\dfrac{a}{p}$, d’où : $1-\dfrac{ar}{S}= \left(1-\dfrac{a}{p} \right)^{1/n},$ c’est-à-dire :

La formule est donc encore vraie au rang n, ce qui achève la démonstration.

Calcul des rayons des cercles inscrits des rangs supérieurs et seconde démonstration du théorème des cercles inscrits égaux

Soit n un entier quelconque supérieur ou égal à 3. Considérons maintenant un triangle du type $AM_{i}M_{i+k}$, formé de k petits triangles consécutifs, avec $2 \leq k \leq n-1$. Il s’agit de montrer que le rayon $r_{n,k,i}$ du cercle inscrit dans ce triangle ne dépend pas de i.

Notons p’, S’ et $a’=M_{i}M_{i+k}$ le demi-périmètre, l’aire et la base du triangle $AM_{i}M_{i+k}$. Calculons de deux manières le rayon $r_{n,1}$ des cercles inscrits dans les petits triangles, d’une part en considérant les n petits cercles inscrits égaux dans
le triangle ABC, d’autre part en considérant les k petits cercles inscrits égaux dans le triangle $AM_{i}M_{i+k}$ :

$r_{n,1}=\dfrac{S}{a}\left[ 1-\left( 1-\dfrac{a}{p} \right)^{1/n} \right] =\dfrac{S’}{a’}\left[ 1-\left( 1-\dfrac{a’}{p’} \right)^{1/k} \right].$

Comme $\dfrac{S}{a}=\dfrac{S’}{a’}$ on tire de l’égalité précédente : $\left( 1-\dfrac{a}{p} \right)^{1/n}=\left( 1-\dfrac{a’}{p’} \right)^{1/k},$ ou encore :

$\dfrac{a’}{p’}=\left[ 1-\left( 1-\dfrac{a}{p} \right)^{k/n} \right].$

On a enfin : $r_{n,k,i}=\dfrac{S’}{p’}=\dfrac{S’}{a’}\dfrac{a’}{p’}=\dfrac{S}{a}\left[ 1-\left( 1-\dfrac{a}{p} \right)^{k/n} \right].$

Le rayon du cercle inscrit dans le triangle $AM_{i}M_{i+k}$ ne dépend donc pas de i, mais seulement de n et de k, ce qui permet de le noter :

Égalité des rayons des cercles par équation barycentrique des droites

Montrer l’égalité des rayons revient à montrer le parallélisme de la droite des centres avec (BC). On veut montrer un parallélisme dans une situation où l’on a de nombreuses relations de récurrence entre les coefficients barycentriques des points en jeu, c’est l’occasion d’un petit traitement par les équations barycentiques des droites.
Bien qu’un peu plus ésotérique, cette approche peut intéresser des collègues ayant en charge des cours de géométrie affine à l’université, comme nouvel exercice de mise en œuvre de ces outils.

Rappel des résultats utilisés

Dans un repère affine (A, B, C), on considère deux points P et Q et leurs coordonnées barycentriques normalisées. Alors un point M appartient à la droite (PQ) ssi le déterminant des coefficients barycentriques des points est nul, ce qui peut s’écrire M.(P Λ Q) = 0 (où Λ désigne le produit vectoriel, et . le produit scalaire).

Avec ces notations (toutes les coordonnées sont normalisées), la parallèle à la droite (IJ) passant par C a pour équation barycentrique C Λ (J - I) = 0.

Classiquement, dans le repère (A, B, C), le centre du cercle inscrit à ABC a pour coordonnées barycentriques (a, b, c).

Avec les notations des paragraphes précédents, Notons I et J les centres des cercles inscrits des triangles $ABM_{n-1}$ et $AM_1C$. On veut montrer que la droite (IJ) est parallèle à (BC) ou encore que C appartient à la droite parallèle à (IJ) passant par B. Dans la suite on notera d le dénominateur noté $D_n$ dans l’onglet TCIEn.

• $M_1$ = $\left(0,\frac{d-x_1-c}{d},\frac{x_1+c}{d}\right)$ dans (A, B, C)
• $M_{n-1}$ = $\left(0,\frac{x_{n-1}+b}{d},\frac{d-x_{n-1}-b}{d}\right)$ dans (A, B, C)
• I = $\left(\frac{d-x_{n-1}-b}{d-b+c},\frac{x_{n-1}}{d-b+c},\frac{c}{d-b+c}\right)$ dans $\left(A,B,M_{n-1}\right)$ et donc
• I = $\left(\frac{d-x_{n-1}-b}{d-b+c},\frac{x_{n-1}}{d-b+c}+\frac{c\left(x_{n-1}+b\right)}{d(d-b+c)},\frac{c\left(d-x_{n-1}-b\right)}{d(d-b+c)}\right)$ dans (A, B, C)
• J = $\left(\frac{d-x_1-c}{d+b-c},\frac{b}{d+b-c},\frac{x_1}{d+b-c}\right)$ dans $\left(A,M_1,C\right)$ et donc
• J = $\left(\frac{d-x_1-c}{d+b-c},\frac{b}{d+b-c}+\frac{x_1\left(d-x_1-c\right)}{d(d+b-c)},\frac{x_1\left(x_1+c\right)}{d(d+b-c)}\right)$ dans (A, B, C).

Avant de poursuivre, remarquons que B est sur la droite C Λ (J - I) ssi les coefficients barycentriques relativement à A de I et de J sont égaux.

Ainsi, démontrer l’égalité des rayons des cercles inscrits des triangles de rang n - 1, revient à montrer la relation $\frac{d-x_{n-1}-b}{d-b+c}=\frac{d-x_1-c}{d+b-c}$,

soit encore : $d\left(x_{n-1}-x_1\right)=(c-b)\left(x_{n-1}+x_1+c+b-d\right)$.

Mais en fait, en utilisant la relation entre d et $K_n$ comme définis à l’onglet précédent, dans la relation de récurrence entre $x_{n-1}$ et $x_1$, soit $d=D_n=2K_n+2x_1+2x_{n-1}+b+c$, la relation à montrer n’est rien d’autre que la relation $\left(E_n\right)$ déjà vue.

Dans ce contexte, l’utilisation d’outils plus sophistiqués n’est qu’une réécriture de ce que l’on cherchait.

Résolution par radicaux du problème pour n = 3

Avant que Dominique Tournès ne trouve les valeurs explicites des rayons des cercles, j’avais cherché une construction dynamique pour le cas n = 3 et, pour, cela cherché à exprimer x et y (des figures de TCIE3) en fonction de a, b et c.

Rappel de la situation : x et y sont les longueurs des deux segments de partage du triangle ABC en trois triangles de cercles inscrits égaux. On a alors :

$(1)\quad (x+b-2y)(2x+2y+b+c)^2 = a^2(x+b+2y)$ ;
$(2)\quad (y+c-2x)(2x+2y+b+c)^2 = a^2(y+c+2x)$.

Et en faisant la somme :

$(3)\quad x^2- y^2 + bx -cy = 0.$

De par sa symétrie, c’est le système de deux équations du 3e degré qui est plus facile à traiter par les logiciels de calcul formel (CF). En effet, proposer l’équation (1) avec l’équation du second degré (3) n’aboutit pas. Par contre on trouve que le système formé par les équations (1) et (2) a en général une solution réelle et deux solutions complexes : on pouvait se douter, pour des raisons de continuité d’un cercle parcourant la bissectrice en B et ses itérés par les symétries convenables, que le système a toujours une et un seule solution réelle.

La solution trouvée par le CF utilise des données partielles très grandes et c’est bien parce que les nombres sont stockés sur des variables multiprécision en Java que l’on peut implémenter cette solution dans un logiciel comme CaRMetal.

On a choisi de calculer la variable x. Elle va être l’expression d’un quotient de $N_x$ par $D_x$ avec

$N_1$ = $4a^4b\left(-a^8-4a^6b^2 +10a^4b^4-4a^2b^6-b^8\right)$ + $8a^4b^2c\left(3a^6-5a^4b^2+a^2b^4+b^6\right)$ + $8a^4bc^2\left(a^6+7a^4b^2+7a^2b^4+b^6\right)$ - $8a^4b^2c^3\left(7a^4+6a^2b^2+3b^4\right)$ - $36a^6b^3c^4$ + $8a^4b^2c^5\left(5a^2+3b^2\right)$ +$ 4a^4bc^7\left(c-2b\right)$

$k_1$ = $11943936a^6\left(a^4-2a^2b^2-2a^2c^2-2b^2c^2+b^4+c^4\right)^3$

$k_2$ = $13824a^4\left(bc^4-b^2c^3-a^2c^3+b^5-a^4b\right)$ + $6912a^4c\left(a^4+b^4+c^4\right)$ - $27648a^4b^3c^2+41572a^6b^2c$

$C_1$ = $\sqrt{k_1+k_2^2}$

$N_2$ = $\left(a^4-b^4+2a^2bc+2b^3c-2a^2c^2-2bc^3+c^4\right)$ $\frac{C_1}{1728}$

$k_3$ = $4a^4b\left(b^4-a^4\right)+2ca^4\left(a^4+6a^2b^2+b^4\right)-8a^4b^3c^2-4a^4c^3\left(a^2+b^2\right)+2a^4c^4\left(2b+c\right)$

$C_2$ = $\left(k_3+\frac{C_1}{3456}\right)^\frac{1}{3}$

$k_4$ = $2a^2\left(b^8-2a^2b^6+2a^6b^2-a^8\right)$ - $4a^2bc\left(a^6-a^4b^2-a^2b^4+b^6\right)$ + $4a^2c^2\left(2a^6-a^4b^2-b^6\right)$ + $4a^2bc^3\left(3a^4+2a^2b^2+3b^4\right)$ - $4a^4c^4\left(b^2+3a^2\right)$ - $12a^2bc^5\left(a^2+b^2\right)$ + $4a^2c^6\left(2a^2+b^2\right)$ + $2a^2c^7(2b-c)$

$N_3$ = $k_4C_2$

$N_4$ = $4(b-c)C_2^4$

$N_x$ = $N_1+N_2+N_3+N_4$

$D_x$ = $a^2C_2^2$, et $x$ = $\frac{N_x}{D_x}$.

Bien entendu y se calcule par l’équation du second degré reliant x et y donnée par (3), soit $y=\frac{-c+\sqrt{4x^2+4xb+c^2}}{2}$.

On notera au passage la robustesse de CaRMetal dans cet exercice sur la figure suivante. En effet, comme on le voit, $N_1$ est d’ordre 13, $k_2$ d’ordre 9, donc $C_1$ aussi. Il en résulte que les calculs intermédiaires effectués utilisent généralement de très grands nombres.

<carmetal|doc=1454|largeur=739|hauteur=518>

On voit bien les limites de l’exercice dans un cadre plus général : si on voulait construire la figure pour le cas n = 5, il faudrait théoriquement calculer tous les segments $x_i$ pour pouvoir construire les points barycentriquement. En pratique toutefois, des précautions logiques sur les constructions dynamiques pourraient permettre de se contenter du premier segment x, mais le calcul dans les partages supérieurs devient de toute façon quasi inaccessible (ou même théoriquement totalement inaccessible) algébriquement.

D’où l’autre piste, pour la construction des figures dynamiques, abordée avec succès par Dominique Tournès qui a réussi à calculer la valeur du rayon du cercle inscrit commun au partage en n cercles (onglet TCIEray).

Exploration de la situation en géométrie hyperbolique

Enfin terminons par une remarque sur la généralisation possible de cette propriété. On sait que le faisceau de Gergonne (et son fameux point) est une propriété absolue, vraie aussi en géométrie hyperbolique ou elliptique, même si dans le cas euclidien on le démontre généralement par les barycentres.

On sait aussi (moins peut-être) que la construction de Malffati — pourtant elle aussi souvent présentée comme conséquence de la cocyclicité — est encore un résultat absolu dont une construction est présentée ici sur une surface pseudosphèrique de Beltrami.

Fort de ces deux exemples, même si l’aire du triangle est bien présente dans ces preuves, il n’est pas tout à fait idiot de se poser la question : qu’en est-il de la version absolue de ce théorème ?

<carmetal|doc=1439|largeur=777|hauteur=530>