L’infini est une droite
En géométrie projective, le plan est prolongé à l’infini par une droite dite de l’infini. Or en prenant un plan (infini, droite de l’infini comprise) en photo, les points de ce plan sont appliqués sur le capteur CCD de façon homographique, ce qui a pour effet d’envoyer un autre plan [1] à l’infini et par contre rendre visible la droite de l’infini, sous forme d’une droite horizontale et appelée d’ailleurs horizon. Ci-dessous, Monsieur Mercator a posé, sur le pays de Rantan [2], des droites d’équation x=1, x=2 etc et x=-1, x=-2 etc. En fait ce sont des demi-droites et leurs origines montrent où est l’axe des abscisses. Monsieur Mercator a posé une bille bleue à l’origine du repère pour distinguer la droite d’équation x=0, des autres :

Les droites d’équations x=k sont parallèles mais elles semblent avoir un point commun, à l’horizon : Leur point de fuite. La droite de l’infini (horizon) est l’ensemble de ces points de fuite.
Voici trois coniques projectives, classées selon leur position par rapport à la droite de l’infini :
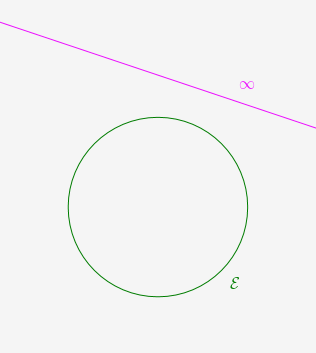
Ellipse : tous les points sont à distance finie

Parabole : Tangente à la droite de l’infini

Hyperbole : Deux points à l’infini
Monsieur Matiyasevitch a posé sur chaque droite d’équation x=k, une bille de coordonnées k et k². Les billes se trouvent alors sur une courbe qui est la parabole d’équation y=x² :

Sans les droites on dirait que cette parabole ressemble à une ellipse (l’axe des ordonnées a été conservé) :
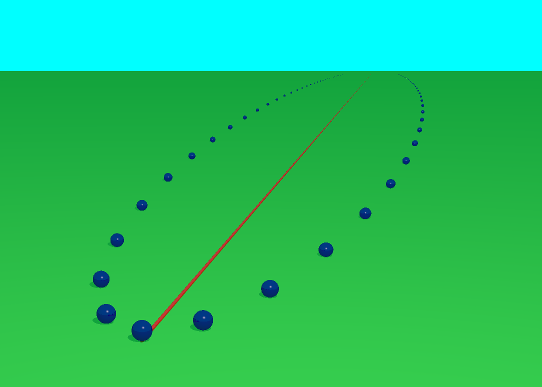
Cet exemple illustre que la nature d’une conique dépend juste de sa position par rapport à la droite de l’infini ; dit autrement, on peut changer l’aspect d’une conique (ellipse, parabole ou hyperbole) selon l’angle de prise de vue de l’appareil photo.
L’infini est un point
Monsieur Mercator a constaté que la planète sur laquelle il vit est en fait posée que le pays vert de Rantan. Le point de contact est le pôle sud de la planète bleue et Monsieur Mercator est debout au pôle nord. Il est muni d’un laser rouge dont le rayon peut traverser la planète :

Monsieur Mercator constate alors que tout point du plan de Rantan peut être éclairé par son laser, en passant par un unique point de la planète : Sa projection de Mercator ou stéréographique. Tout le plan de Rantan peut être, par projection stéréographique, dessiné sur la sphère bleue, dite de Riemann. Et toute la sphère de Riemann, à l’exception du pôle nord, correspond à un point du plan. Alors la tentation est grande de dire que le pôle nord, c’est l’infini.
De fait, puisque les pôles nord et sud sont interchangeables par symétrie par rapport à l’équateur, 0 et l’infini sont interchangeables par inversion par rapport à un cercle, qui est la projection stéréographique de l’équateur sur le plan. Mais aussi par la composition de l’inversion par la conjugaison complexe, c’est-à-dire par la fonction « inverse » 1/z. Alors, dire que la fonction f(z) tend vers 2 en l’infini, c’est dire que la fonction f(1/z) tend vers 2 en 0. Et de même, dire que f(z) tend vers l’infini en l’infini, c’est dire que 0 est un pôle de f(1/z). Cette possibilité de prolonger par continuité certaines fonctions (au moins les fractions rationnelles) à l’infini sur la sphère de Riemann, est à la base des travaux de Fatou, Julia, Mandelbrot et quelques autres sur l’itération des fonctions complexes.
En apparence il y a contradiction entre la sphère de Riemann sur laquelle l’infini n’est qu’un point (le pôle nord) et le plan projectif dans lequel l’infini est une droite. En fait, il n’y a pas de contradiction, puisque le plan projectif n’étant pas orientable, la sphère de Riemann n’est pas un plan projectif. Oui mais alors c’est quoi ? Une droite projective. Sauf que c’est la droite complexe à laquelle on a ajouté l’unique complexe infini. Et on l’a rajouté à l’infini, qui est un point.
En fait, la droite projective complexe est bien plus complexe qu’il n’y paraît puisque du fait que l’infini (le pôle nord) peut être approché de bien des manières différentes, la fonction exponentielle complexe n’a pas de limite, ni finie ni infinie, en l’infini (par exemple en -∞ et en +∞ les limites ne sont pas les mêmes : Gaston Julia parle de singularité essentielle de l’exponentielle en l’infini.
Pour mieux y voir pourquoi pas regarder du côté de la droite projective réelle ?
Droite projective
La version monodimensionnelle de la sphère de Riemann est le cercle de Riemann : La projection stéréographique sur un cercle donne à celui-ci une structure de droite projective :

Ce rajout d’un point à l’infini à la fois aux deux bouts de la droite réelle, permet déjà de montrer comment sur une droite projective, Buzz peut aller « au-delà de l’infini » : Il lui suffit de ne pas bouger puisque, une fois qu’on a dépassé les réels du côté de +∞, on en revient du côté de -∞, et chaque point du cercle autre que le pôle nord est à la fois des deux côtés de l’infini. En fait cela traduit essentiellement la non-orientabilité de la droite projective.
La fonction 1/x est illustrée par une symétrie axiale, laissant 1 et -1 invariants (ils sont leurs propres inverses) mais échangeant 0 et l’infini.
On peut voir, avec le nomogramme circulaire de Clark, que 0 est élement absorbant pour la multiplication. Mais par symétrie axiale, il en sera alors de même pour l’infini : 2×∞=∞. Et comme un élément absorbant est en général unique, on conçoit que 0×∞ ne peut rien donner de cohérent avec ce qui précède : La fameuse forme indéterminée.
Mais l’idée que +∞ et -∞ sont « au même endroit » rend la droite projective peu propice à l’exploration des limites. On a donc besoin d’une autre approche dans le cas réel, consistant à rajouter +∞ tout à droite et -∞ tout à gauche.
Compactifions
Alexandrov est en quelque sorte celui qui tourne les crochets : Comme R est un intervalle ouvert : ]-∞;+∞[, on le transforme en intervalle fermé (et compact, voir plus bas) en tournant les crochets : [-∞;+∞] : Et voilà le compactifié d’Alexandrov !
En fait la construction est très rigoureuse, elle consiste à transformer la demi-droite des réels positifs en un segment (avec ajout d’un élément supérieur à tous les réels positifs, soit +∞) et la demi-droite des réels négatifs en un autre segment (par rajout de -∞ qui est inférieur à tous les réels négatifs). La fonction Math.atan permet de ramener l’ensemble des réels à un segment ouvert et donc de voir le compactifié d’Alexandrov :

La norme IEEE 754 définit la manière dont sont représentés les nombres réels (« flottants ») dans une machine ayant un nombre fini d’états : Si on essaye de multiplier un grand nombre de fois une quantité par 1000, on risque d’arriver à un dépassement de capacité :

Une fois que la variable geant a dépassé environ 10308, elle est considérée comme infinie et toute tentative de la multiplier par un nombre positif la rendra toujours égale à l’infini : On dit que l’infini est élément absorbant pour la multiplication dans le compactifié d’Alexandrov.
Le script suivant (de CaRMetal) est un cas classique de boucle à condition de sortie :
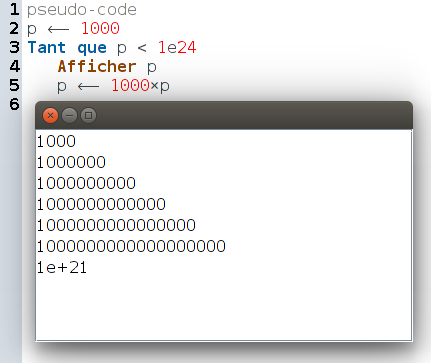
(il s’agit de l’affichage de quelques termes d’une suite géométrique).
Mais cette variante, malgré les apparences, boucle aussi un nombre fini de fois :
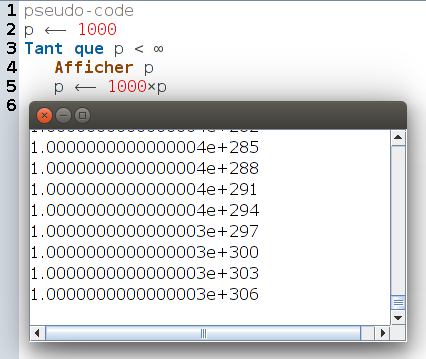
En y réfléchissant, ce n’est pas surprenant : La place mémoire étant limitée dans l’ordinateur, il vient un moment où l’infini est atteint concrètement, sous la forme d’un dépassement de capacité de la machine.
Avec CaRMetal
JavaScript (langage de programmation de CaRMetal, ici déguisé en pseudo-code) cherche à éviter le plus possible les blocages et des tentatives de division par 0 ou de calcul de ln(0) n’y mènent pas à des erreurs de division par 0 ou de domaine de définition, mais à des calculs de limite. Le script suivant nous apprend que la division de 1 par 0 donne un résultat affiché comme Infinity :

En fait le mode pseudo-code de CaRMetal donne un affichage « joli » qui ne montre pas l’orthographe Infinity de JavaScript. Si on a des trous de mémoire, le calcul 1/0 est plus facile à entrer, que Infinity. On verra plus bas qu’avec Python cette astuce ne fonctionne pas, Python étant plus « classique » que JavaScript sur la division par 0.
Voici quelques expériences menées avec des additions :
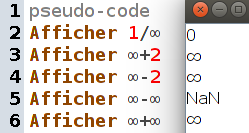
Et leurs traductions dans le langage d’IEEE 754 et des limites :
| un nombre trop grand pour être représenté en machine a un inverse concrètement égal à 0 | la limite de l’inverse d’une fonction tendant vers l’infini, est 0 |
| Une fois dépassée la capacité de la machine, ajouter 2 ne fait qu’aggraver les choses | La limite de la somme d’une fonction tendant vers l’infini et d’une fonction tendant vers 2, est l’infini |
| Une fois dépassée la capacité de la machine, soustraire 2 ne suffit pas à arranger les choses | La limite de la somme d’une fonction tendant vers l’infini et d’une fonction tendant vers -2, est l’infini |
| Tenter de compenser un dépassement de capacité vers le haut par un dépassement de capacité vers le bas, peut mener à un résultat imprévisible | La différence entre deux fonctions tendant vers l’infini, est indéterminée |
| Une fois dépassée la capacité de la machine, dépasser une deuxième fois ne fait qu’aggraver les choses | La limite de la somme d’une fonction tendant vers l’infini et d’une fonction tendant vers l’infini, est l’infini |
En bref, l’infini est absorbant pour l’addition ; son opposé aussi donc leur somme est indéterminée.
Et des expériences sur la multiplication :

| Une fois dépassée la capacité de la machine, dépasser une deuxième fois ne fait qu’aggraver les choses | La limite de la somme d’une fonction tendant vers l’infini et d’une fonction tendant vers l’infini, est l’infini |
| Une fois dépassée la capacité de la machine, doubler le résultat ne fait qu’aggraver les choses | La limite du produit d’une fonction tendant vers l’infini et d’une fonction tendant vers 2, est l’infini |
| Une fois dépassée la capacité de la machine, élever au carré ne fait qu’aggraver les choses | Lorsque deux fonctions tendent vers l’infini, leur produit tend vers l’infini |
| Une fois dépassée la capacité de la machine, multiplier par un nombre très petit ne suffit pas forcément à compenser le résultat | Lorsqu’une fonction tend vers l’infini et une autre vers 0, leur produit est indéterminé |
En bref, l’infini est absorbant pour la multiplication ; 0 aussi donc leur produit est indéterminé.
Enfin des expériences sur les fonctions classiques :

| Dans le compactifié d’Alexandrov, ln est définie en 0 et vaut -∞ | La limite de ln en 0 vaut -∞ |
| Une fois dépassée la capacité de la machine, prendre le logarithme ne compense pas ce dépassement | La limite de ln en +∞ est +∞ |
| L’exponentielle est définie sur tout le compactifié d’Alexandrov et prend la valeur 0 en -∞ | La limite de l’exponentielle en -∞ est nulle |
| L’exponentielle est définie sur tout le compactifié d’Alexandrov et prend la valeur +∞ en +∞ | La limite de l’exponentielle en +∞ est infinie |
La Numworks
La calculatrice Numworks est programmée en C++, langage qui connaît la norme IEEE 754. Ce qui permet de bonnes surprises, comme celle-ci (en haut, 1/0 donne une erreur non de division par 0 mais de nombre indéterminé) :

Oui, sans passer par le calcul formel (de limites), la Numworks sait que la limite de 1/x en l’infini est 0 et que la limite de ln(x) en 0 est -∞. Elle sait aussi que la limite de ln(x) en +∞ est +∞ (avec un doute sur la limite de l’exponentielle en +∞ ; on expliquera ça plus bas) :

La Numworks sait aussi que la limite de l’exponentielle en -∞ est 0 et que la somme de deux fonctions tendant vers l’infini, tend aussi vers l’infini, ainsi que le produit d’une fonction tendant vers 2 et d’une fonction tendant vers l’infini :

On peut considérer la Numworks comme une calculatrice « deux en un » avec une application calculatrice décrite ci-dessus, et une autre application de type calculatrice, la console de Python :
Version Python
En Python, contrairement à JavaScript, 1/0 donne une erreur de division par 0 mais on peut créer un flottant de type « inf » qui donne l’infini. Pour profiter de la concision de Python, on va, au lieu des 4 lettres de buzz, utiliser les deux lettres oo qui évoquent vaguement le symbole ∞ [3].
Les expériences sur les additions qui avaient été menées ci-dessus avec CaRMetal donnent ceci en Python :
oo=float("inf")
print(1/oo)
print(oo+2)
print(oo-2)
print(oo-oo)
print(oo+oo)Et elles affichent ceci sur la Numworks :

Les expériences sur la multiplication menées avec CaRMetal, transposées en Python :
oo=float("inf")
print(oo+oo)
print(oo*2)
print(oo*oo)
print(oo*0)donnent

Et les fonctions classiques, qu’on récupère avec le module math de Python :
from math import *
oo=float("inf")
print(log(0))
print(log(oo))
print(exp(-oo))
print(exp(oo))Avec SofusPy on a :
-inf
inf
0.0
infMais la Numworks donne une erreur de domaine (0 n’est pas censé avoir de logarithme sur la Numworks alors que dans Python 2 il en a un, qui est -∞ comme en JavaScript).
Allo NaN mais allo quoi !
Le « nombre de Magritte » [4] NaN est aussi un animal particulièrement exotique du zoo IEEE 754. On le trouve dans deux cas assez distincts : Lorsqu’on essaye de calculer une forme indéterminée comme on l’a vu plus haut, mais aussi lorsqu’on essaye de calculer une limite qui n’existe pas :
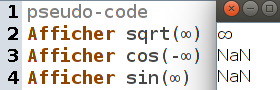
Le comportement de la norme IEEE754 vis-à-vis des fonctions est assez simple et logique :
- Si une fonction f tend vers l’infini en 0, on la considère comme définie en 0, et f(0)=∞ (cas de 1/x et ln(x)) ;
- Si une fonction f tend vers une limite L en l’infini, elle est considérée comme définie en ∞ et f(∞)=L ; ceci, même si L=∞ ;
- Si une fonction f n’a pas de limite en ∞ ou que sa limite est indéterminée, on considère qu’elle est définie quand même mais f(∞)=NaN (nan en Python, undef avec la Numworks).
- Dans tous les cas, f(NaN)=NaN (par exemple le carré d’un nombre indéterminé est lui-même indéterminé).
JavaScript est donc totalement conforme à la norme, Python 2 l’est moins, Python 3 encore moins, et la Numworks est depuis la version 1.8.1 la seule calculatrice en partie conforme à cette norme, en entrant les trois lettres inf pour simuler l’appui sur la touche ∞, inexistante (ainsi que la touche NaN) sur toutes les calculatrices, Numworks comprise.
Mais pourquoi la Numworks ne connaît-elle pas la limite de l’exponentielle en l’infini ? Probablement parce que les nombres de base dans la Numworks sont non les flottants de C++, mais les complexes. Or s’il paraît naturel de dire que e+∞=+∞ et e-∞=0, on vient de voir par la trigonométrie que ei∞=cos(∞)+i sin(∞)=NaN+i NaN = NaN. Les fonctions transcendantes comme ez et ln(z) (ainsi que les fonctions trigonométriques ou hyperboliques) sont dites avoir une singularité essentielle en ∞. On a vu avec la construction de la sphère de Riemann que cela revient à dire que leur composée par 1/z a une singularité essentielle en 0. La représentation graphique de sin(1/x) donne une idée de la complexité de ce genre de situation (sin(1/z) a une singularité essentielle en 0) :
(graphique obtenu avec Wolfram alpha).
Comme l’infini est le pôle nord de la sphère de Riemann, on peut donc résumer la situation actuelle à ceci : Alors que la norme IEEE754 se place naturellement dans le compactifié d’Alexandrov, la Numworks, par le choix des complexes, est plus orientée « géométrie projective ».
Mais rien n’est perdu, a priori : Lorsqu’on calcule 4/6 avec la Numworks, la fraction est simplifiée : La Numworks sait que 4/6 n’est pas n’importe quel complexe. D’ailleurs si on essaye de calculer ln(i) la Numworks affiche un message d’erreur. Il n’y a donc aucune raison que la norme IEEE754 soit exclue d’une calculatrice qui ne calcule de toute façon pas sur les nombres complexes lorsqu’intervient une fonction avec singularité essentielle.
Et au-delà
Dans le disque de Poincaré l’infini est un cercle appelé horizon par Poincaré. Voici une droite du plan hyperbolique dans ce modèle (en rouge). Il y a été ajouté (en bleu) des points obtenus par construction itérée de symétries centrales, comme des perles sur un collier, ou des graduations sur la droite rouge :
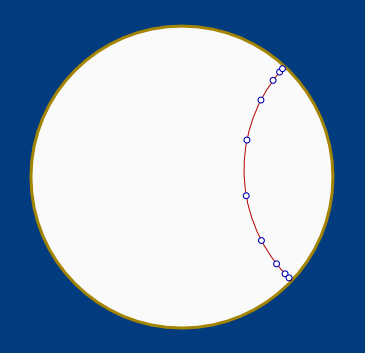
On voit alors que la droite rouge a deux points à l’infini (dits « idéaux ») qui sont représentés par les intersections de l’arc de cercle rouge (la droite hyperbolique) et de l’horizon. Alors, si on continue à glisser sur le cercle au-delà de l’arc de cercle, on va au-delà de l’horizon, c’est-à-dire, du point de vue de la géométrie hyperbolique, au-delà de l’infini ! C’est donc dans la zone bleue foncée qu’un Buzz hyperbolique irait au-delà de l’infini.
Annexes
IEEE754 en classe
Voici une séquence de cours [5] sur le codage des flottants par IEEE754, ou plutôt des versions simplifiées à 8 ou 16 bits (pages html à ouvrir dans un autre onglet du navigateur) :
| codage simplifié sur 8 bits | extension aux très petits et très grands nombres | version 16 bits |
Et voici l’énoncé d’un devoir maison sur la représentation des flottants [6] :
| le sujet | son source |
Enfin la norme elle-même :
Les scripts PovRay
Les droites parallèles avec point de fuite :
#version 3.7;
#include "colors.inc"
camera {
location <-4.0, 5.0, 16.0>
direction 1.5*z
right x*image_width/image_height
look_at <0.0, 0.8, 0.0>
}
light_source { <-5,10,8> White}
sky_sphere { pigment { Cyan }}
#declare nombre=1;
sphere {
<0, 0.2, 0>, 0.2
texture { pigment {Blue}
finish {reflection 0.04 diffuse 0.1 phong 0.4 phong_size 101}
}
}
#while(nombre<20)
cylinder {
<nombre,0,0>,
<nombre,0,-2000>,
0.04
texture { pigment {Red} finish { ambient 0.4 diffuse 0.2 reflection 0.04 } }
}
cylinder {
<-nombre,0,0>,
<-nombre,0,-2000>,
0.04
texture { pigment {Red} finish { ambient 0.4 diffuse 0.2 reflection 0.04 } }
}
#declare nombre=nombre+1;
#end
cylinder {
<0,0,0>,
<0,0,-2000>,
0.04
texture { pigment {Red} finish { ambient 0.4 diffuse 0.2 reflection 0.04 } }
}
plane {
y,
-0.01
texture { pigment {rgbf <0.1,0.8,0.1,0.4> } }
}La parabole dans le plan projectif :
#version 3.7;
#include "colors.inc"
camera {
location <-2.0, 4.0, 8.0>
direction 1.5*z
right x*image_width/image_height
look_at <0.0, 0.8, 0.0>
}
light_source { <-5,10,8> White}
sky_sphere { pigment { Cyan }}
#declare nombre=1;
sphere {
<0, 0.2, 0>, 0.2
texture { pigment {Blue}
finish {reflection 0.8}
}
}
#while(nombre<40)
sphere {
<nombre, 0.2, -nombre*nombre>, 0.2
texture { pigment {Blue}
finish {reflection 0.8 }
}
}
sphere {
<-nombre, 0.2, -nombre*nombre>, 0.2
texture { pigment {rgbf <0.2,0.2,0.8,0.4>}
finish {reflection 0.8}
}
}
#declare nombre=nombre+1;
#end
cylinder {
<0,0,0>,
<0,0,-2000>,
0.04
texture { pigment {Red} finish { ambient 0.4 diffuse 0.2 reflection 0.04 } }
}
plane {
y,
-0.01
texture { pigment {rgbf <0.1,0.8,0.1,0.4> } }
}La sphère de Riemann :
#version 3.7;
#include "colors.inc"
camera {
location <-4.0, 5.0, 16.0>
direction 1.5*z
right x*image_width/image_height
look_at <0.0, 0.8, 0.0>
}
light_source { <-5,10,8> White}
sky_sphere { pigment { Cyan }}
sphere {
<0, 2, 0>, 2
texture { pigment {rgbf <0.1,0.1,0.8,0.99>}
finish {reflection 0.004 diffuse 0.1 phong 0.4 phong_size 101}
}
}
cylinder {
<0,4,0>,
<4,-6,20>,
0.04
texture { pigment {Red} finish { ambient 0.4 diffuse 0.2 reflection 0.04 } }
}
plane {
y,
-0.01
texture { pigment {rgbf <0.1,0.8,0.1,0.4> } }
}Le bouton de l’infini
Une revendication d’élèves de terminale STI2D semble plutôt pertinente : Qu’il y ait un bouton « ∞ » sur la calculatrice. L’infini serait alors considéré [7] comme une constante comme π, e et i (qui ont déjà droit à des boutons) et on calculerait sur ce « nombre » à l’aide du standard IEEE-754.
En manipulant en ligne cette calculatrice [8], on peut se faire une idée de l’expérience utilisateur qu’elle permet (cependant pas de calcul scientifique et le bouton « i » est inopérant) :
|
|
Et voici la page html à télécharger pour utilisation en local :


Commentaires