L’actualité aidant, tout a tourné autour de cet exemple :
| Des élections se préparent dans une commune ; Paul Bismuth, qui est candidat à ces élections, « fera » 17% le jour des élections. Mais il ne le sait pas, puisque les élections n’ont pas encore eu lieu ! Alors il commandite un sondage, consistant à demander à 100 électeurs s’ils voteront pour lui. On se propose d’étudier la variable aléatoire « nombre d’électeurs de Paul Bismuth parmi les 100 personnes sondées ». |
I/ Avec la loi binomiale
D’après les données de l’énoncé, la probabilité qu’un électeur choisi au hasard vote Bismuth, est 0,17. Donc le nombre d’électeurs de Paul Bismuth parmi les 100 suit une loi binomiale de paramètres 100 et 0,17.
1) Probabilités
- Quelle est la probabilité que parmi les 100 personnes, exactement 17 votent pour Paul Bismuth ?
On lance le calculateur de probabilité de lois binomiales, et on entre les données souhaitées. Un petit problème est que le calculateur de probabilités binomiales ne sait calculer que des probabilités d’appartenance à des intervalles. Ici, « être égal à 17 » veut dire « appartenir à l’intervalle [17 ;17] » :

Il y a donc environ une chance sur 10 que l’échantillon donne le score exact de Monsieur Bismuth. Autrement dit, les journalistes ont environ 9 chances sur 10 de se tromper en publiant des estimations ponctuelles plutôt que des intervalles de confiance (voir plus bas).
- Quelle est la probabilité que Monsieur Bismuth fasse au moins autant que le sondage précédent, qui lui donnait 22% ?
Il suffit de modifier les bornes de l’intervalle ; ici, « être au moins égal à 22 » veut dire « être dans [22 ;100] » :
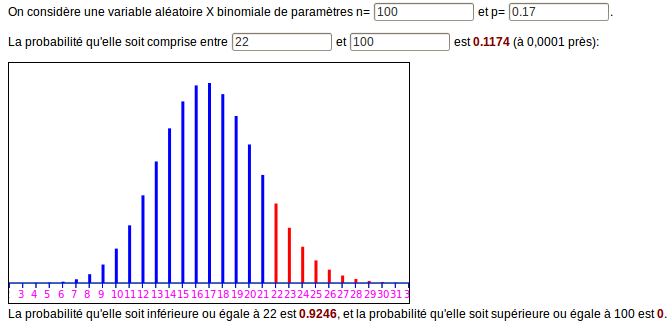
- Quelle est la probabilité que l’échantillon attribue à Paul Bismuth, un score entre 10% et 24% ?
Encore une fois, on modifie juste les bornes de l’intervalle :
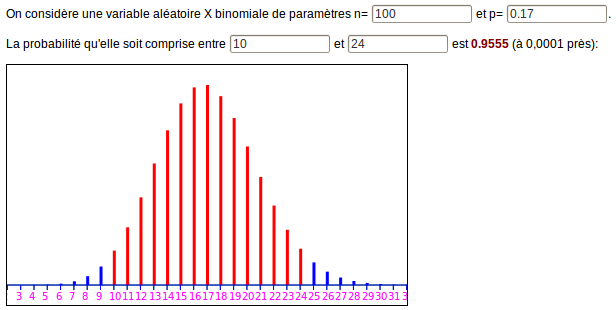
On constate que la probabilité est voisine de 0,96 ; et on se demande s’il y avait un moyen de trouver les bornes de l’intervalle autrement que par tâtonnements :
2) Intervalles de fluctuation
Pour déterminer un intervalle de fluctuation à 95%, on ouvre le calculateur d’intervalles de fluctuation et on entre à nouveau les paramètres 100 et 0,17 :
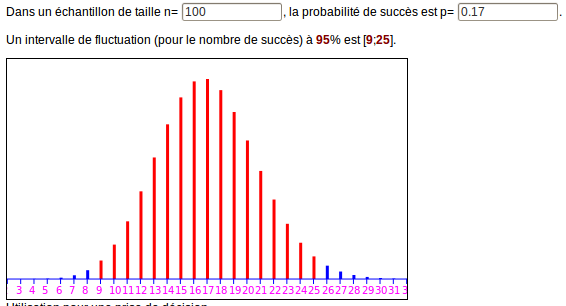
On constate que l’algorithme du document d’accompagnement dépasse par prudence, les bornes trouvées empiriquement.
En cochant l’option « dessiner l’approximation normale », on voit que celle-ci est plutôt bonne, ce qui incite à refaire l’exercice avec la loi normale.

II/ Loi normale
1) Calcul des paramètres
On calcule
- EX = 100×0,17 = 17
- σ X = √(100×0,17×0,83)≈3,756
2) Calculs de probabilités
On démarre alors le calculateur de probabilités normales ; on entre ensuite les paramètres calculés ci-dessus ; mais si on essaye de calculer la probabilité que la variable aléatoire normale soit comprise entre 17 et 17 (autrement dit, égale à 17), on trouve 0 :

En effet, une intégrale (en vert ci-dessus) dont les bornes inférieure et supérieure sont égales, est nulle. On doit donc appliquer une correction de continuité, qui revient à dire que pour une loi normale approchant une loi à valeurs entières, « être égale à 17 » veut dire « être comprise entre 16,5 et 17,5 ». La probabilité devient alors à nouveau d’une chance sur 10 environ (intégrale en cyan ci-dessous) :
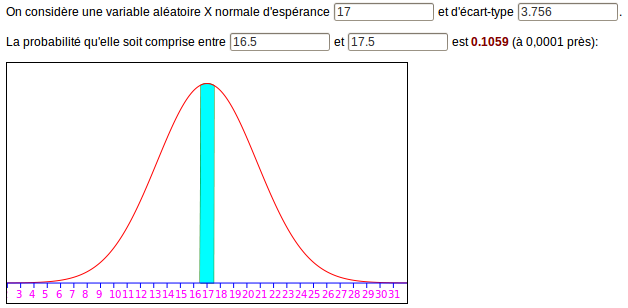
L’erreur d’approximation est de 0,0002 soit en valeur relative, environ 0,2% ce qui est plutôt bon.
De même, pour avoir la probabilité que le pourcentage de Paul Bismuth soit au moins 22%, on calcule l’intégrale entre 21,5 et +∞ :
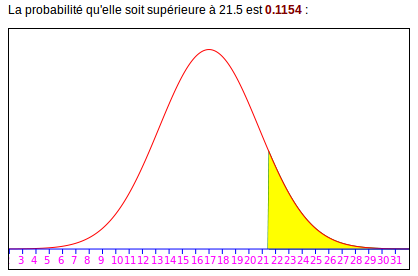
L’erreur d’approximation est encore une fois 0,002 en valeur absolue et 0,2% en valeur relative.
Et la probabilité que le pourcentage de Paul Bismuth soit entre 10 et 24, est approchée par l’intégrale entre 9,5 et 24,5 :
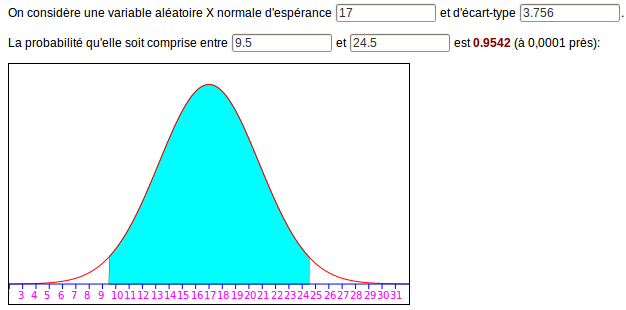
L’erreur d’approximation est 0,0007 en valeur absolue donc moins de 0,1% en valeur relative...
Comme avec la loi binomiale, on peut vouloir un outil qui permet de passer des 0,95 (la probabilité) à l’intervalle (l’évènement) sans avoir à tâtonner. Cet outil existe, c’est l’intervalle de fluctuation asymptotique.
On ouvre donc le calculateur d’intervalles de fluctuation asymptotiques et on entre une troisième fois les paramètres de la loi binomiale 100 et 0,17. L’intervalle de fluctuation asymptotique apparaît alors arrondi à l’entier :
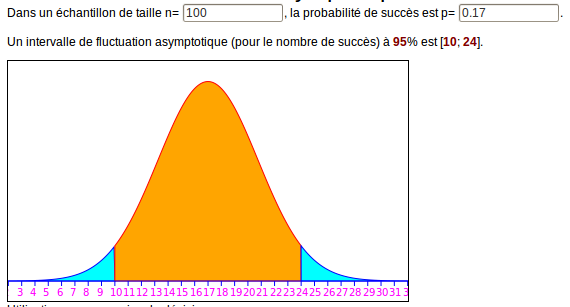
Le sondage à 22% qui avait tant fait rêver Monsieur Bismuth avant sa déconvenue, est donc « conforme » puisque le nombre 22 se trouve à l’intérieur de la zone orangée (qui représente l’intervalle de fluctuation asymptotique). On peut d’ailleurs dessiner la droite d’équation x=22 en entrant le nombre 22 dans la case en-dessous du dessin et en cochant la case idoine. Inversement, le pourcentage obtenu aux élections (17%) est, lui, dans l’intervalle de confiance à 95% :
III/ Intervalle de confiance
Retour en arrière : Paul Bismuth est angoissé quelques semaines avant les élections, et un journal local publie les résultats d’un sondage, qui, sur 100 personnes, lui attribue 22 électeurs. Le journal a alors publié cet entrefilet :
| À un mois des élections, les citoyens sont toujours indécis, mais l’opposition est de plus en plus vivace, 22% des électeurs ayant l’intention de voter Bismuth. |
Ceci est malhonnête puisque les bornes de l’intervalle ne sont pas publiées, ni aucun moyen de les retrouver (par exemple la taille de l’échantillon). Pour en savoir plus, on peut calculer l’intervalle de confiance avec le calculateur d’intervalles de confiance, puis on entre les données (100 pour la taille de l’échantillon, et 0,22 pour la fréquence mesurée) :
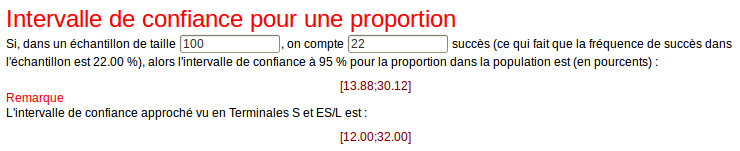
Paul Bismuth peut donc difficilement porter plainte contre l’institut de sondage, puisque son score se trouve à l’intérieur de l’intervalle de confiance.
La séquence ci-dessus durant un peu plus d’une demi-heure, on a le temps de recommencer une partie de celle-ci avec une taille d’échantillon plus raisonnable : 1000. Alors le nombre moyen de succès est 170 et la probabilité de l’atteindre est nettement plus petite que dans le cas précédent :
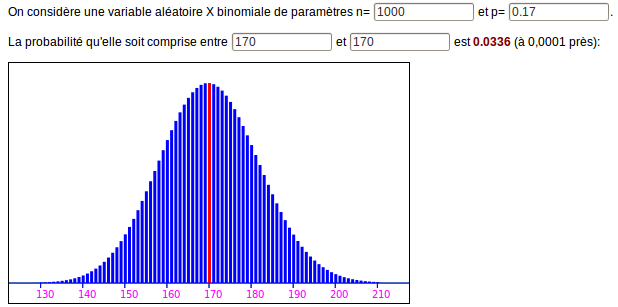
De même, l’intervalle de fluctuation asymptotique est nettement plus reserré qu’avant (on n’y trouve pas par exemple les 22% vus ci-dessus) :
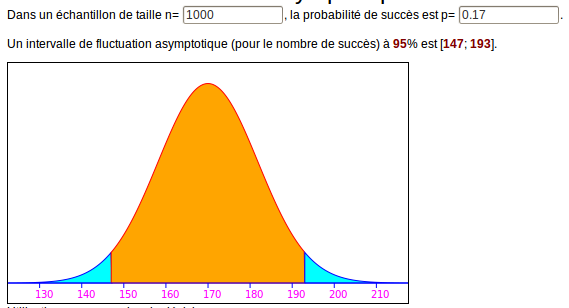
Vérification avec la loi binomiale :
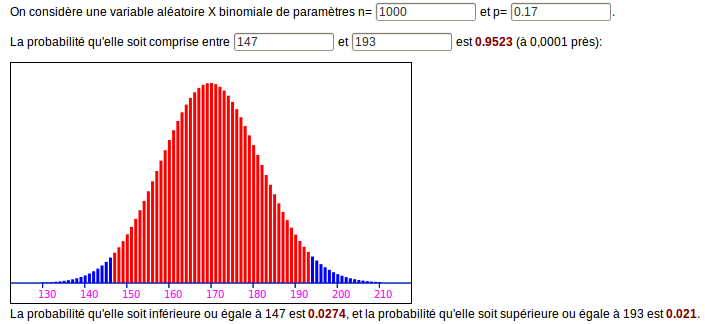

Commentaires