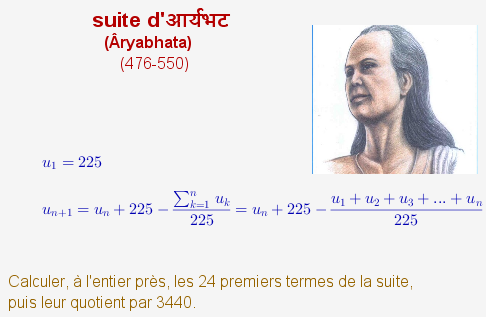
La plus vieille table trigonométrique avait un pas de 3,75°. Elle fut établie avant l’époque de Charlemagne, en Inde. Il semble que son auteur ait utilisé la suite récurrente ci-dessous. Cette suite est intéressante à étudier du point de vue algorithmique parce son terme courant est calculé récursivement à partir de la somme des termes précédents, ce qui algorithmiquement parlant, nécessite une boucle à l’intérieur d’une autre boucle :
Pour échapper à cette complexité algorithmique, on peut faire l’activité sur tableur, en réservant par exemple la colonne B pour le calcul de la suite, et la colonne C pour le calcul de la somme des termes, avec
=SOMME(B$2;B2)
dans C2, à copier vers le bas...
Si les ordinateurs n’utilisent plus CORDIC de nos jours, qu’utilisent-ils ? L’algorithme se résumerait [1] à ceci :
- Calcul de la mesure principale de l’angle x, pour revenir à un intervalle comme $[-\pi ;\pi]$ ;
- Recherche sur cet intervalle, d’un approximant de Padé ;
- Calcul du numérateur et du dénominateur de cet approximant, par la méthode de Horner ;
- Division des deux nombres précédents dans le coprocesseur FPU du Pentium.
C’est la première étape qui se prête le mieux à une activité algorithmique en Première.
Une fois qu’on en est arrivé à chercher le sinus ou le cosinus d’un angle compris entre $-\pi$ et $\pi$, on a besoin d’une fraction rationnelle qui soit proche du sinus ou du cosinus sur l’intervalle $[-\pi ;\pi]$. Pour cela, un logiciel de calcul formel [2] fait l’affaire. Par exemple WxMaxima, qui passe par un développement limité, alors qu’Xcas donne directement l’approximant de Padé : Xcas a donc été choisi ici :

De plus, il est possible de sélectionner sous Xcas le résultat du calcul, de le copier (par Ctrl+C) puis de le coller (par Ctrl+V) dans un logiciel de géométrie dynamique et de représenter graphiquement la fonction [3]. Avec CaRMetal, après avoir ajouté les représentations graphiques des fonctions rcos et rsin, on obtient ceci :
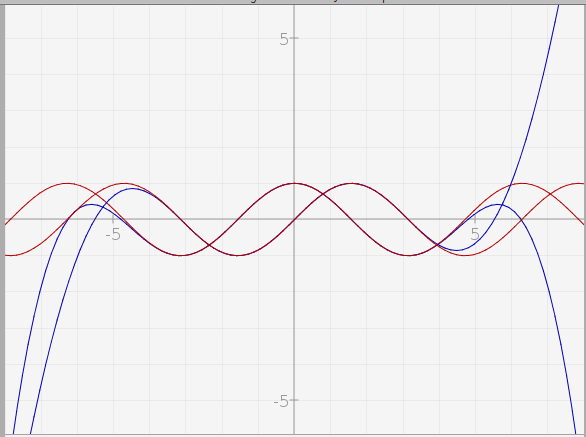
Un plan possible pour un TP est le suivant :
- Chercher par les formules de trigonométrie, un intervalle dans lequel faire l’approximation ;
- écrire un algorithme qui, à partir de $x \in \R$, donne sa valeur principale ;
- obtenir les approximants de Padé avec un logiciel de calcul formel ;
- représenter graphiquement les approximants et les fonctions ;
- vérifier la qualité de l’approximation.
Voici un exemple de TP d’une heure :
On peut envisager un prolongement pour les élèves ayant déjà vu Horner en Seconde, sur le calcul effectif des fractions rationnelles.

Commentaires