La preuve par induction (logique), souvent pratiquée dans les sciences expérimentales, utilise comme point de départ, des faits qui sont perçus ou induits : Elle va du connu vers le moins connu, et se trouve souvent entachée d’erreurs ou de risque.

Un exemple connu :

l’erreur de Fermat :

$2^{2^0}+1=3$ est premier ;

$2^{2^1}+1=5$ est premier ;

$2^{2^2}+1=17$ est premier ;

$2^{2^3}+1=257$ est premier ;

$2^{2^4}+1=65537$ est premier ;

Donc $2^{2^5}+1=4294967297$ est premier

En fait, Fermat avait, fidèle à son style, présenté ce résultat comme une conjecture. Son « erreur » est juste de ne pas avoir pensé à vérifier la non-divisibilité par des nombres congrus à 1 modulo 128, dont Euler a prouvé un siècle après que ce sont les seuls diviseurs possibles d’un nombre de Fermat, et la preuve d’Euler utilisait des outils mathématiques que Fermat avait à sa disposition.

Au contraire, la déduction logique part d’axiomes (qui ne sont pas perçus mais conçus) pour aller vers des théorèmes, par une construction allant vers une vérité croissante (techniquement, par une relation d’ordre dans une algèbre de Lindenbaum). Les hypothèses ne viennent donc pas de l’expérimentation mais sont des constructions logiques faites une fois pour toutes en préambule de la déduction : Sous réserve que ces axiomes soient vrais, la théorie qui en résulte l’est aussi.

Or le travail de déduction des théorèmes à partir d’axiomes ou de lemmes, est largement mécanisable. Le projet, lancé par Leibniz vers 1700, a abouti à la création d’un langage de programmation (Prolog) puis de logiciels de démonstration automatique comme Coq (logiciel) ou Isabelle (logiciel). Parmi ces outils permettant de démontrer, voire découvrir, des théorèmes de géométrie, on ne considèrera ici que ceux qui sont interfacés avec des logiciels de géométrie dynamique (dans les onglets suivants).

L’un des premiers de ces logiciels était GeoProof, au demeurant l’un des premiers logiciels reconnaissant les formats Kig et C.a.R., mais il est « discontinué » et loin d’être multiplateforme...

Géometrix semble le plus ancien des logiciels de ce genre (développé en Pascal (langage) avec un moteur de déduction en Prolog), à en juger par la date de 1990 affichée sur le site. Le logiciel a été magnifiquement décrit par son auteur sur MathemaTICE dès 2006. Dans sa version de 2013 (en cours d’élaboration à l’heure où j’écris ces lignes, et hélas seulement sous Windows pour l’instant), le moteur d’inférence de Géométrix tourne en tâche de fond, ce qui lui permet d’afficher des faits déduits en temps presque réel : Au cours de la construction de la figure, les théorèmes sont produits automatiquement. Géométrix s’éloigne donc un peu de la géométrie dynamique, les conjectures n’étant pas seulement visuelles mais également suggérées par le logiciel. Pour utiliser Géométrix, on a le choix entre la version élève (qui ne fait que conjecturer) et la version professeur (qui, en plus, affiche sur demande la démonstration en Prolog de la propriété conjecturée). En effet, ce logiciel a pour but essentiel de permettre la conception d’exerciciels de démonstration en géométrie.

Donc, le plus dur pour démontrer que E est le milieu de [AF] (les noms des points ont changé par rapport à la figure ci-dessus) c’est de commencer la construction. En effet, le menu de construction des points n’a pas de point libre dans le plan :

Conseil préliminaire : Bien regarder les vidéos de tutoriels sur le site avant de commencer une activité avec Géométrix. En effet, son comportement est parfois si différent des logiciels de géométrie dynamique classiques, qu’on ne sait pas toujours comment faire, ni même ce qu’on peut faire.

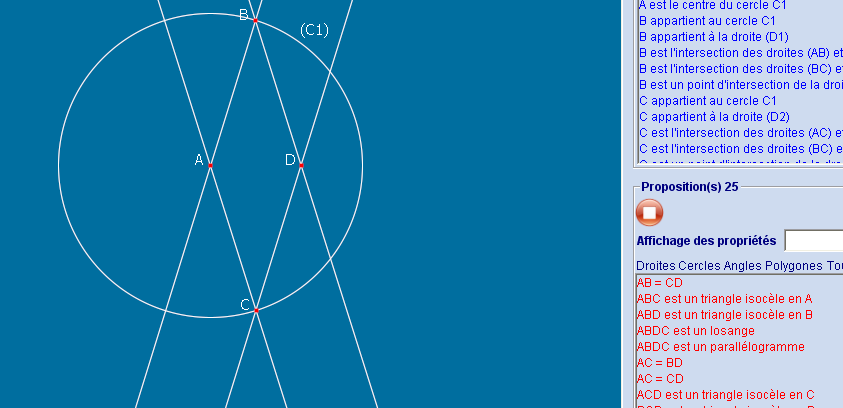
Dans le cas présent, quelques tentatives ont mené à la découverte du célèbre double-clic sur la figure, qui se charge de construire un point libre, avec une suggestion de nom pour celui-ci (A puis B etc.). Pour avoir un losange, on peut placer C sur le cercle de centre A passant par B, pour garantir que AB=AC. Pour compléter le losange, on peut construire des parallèles [1] puis leur intersection :

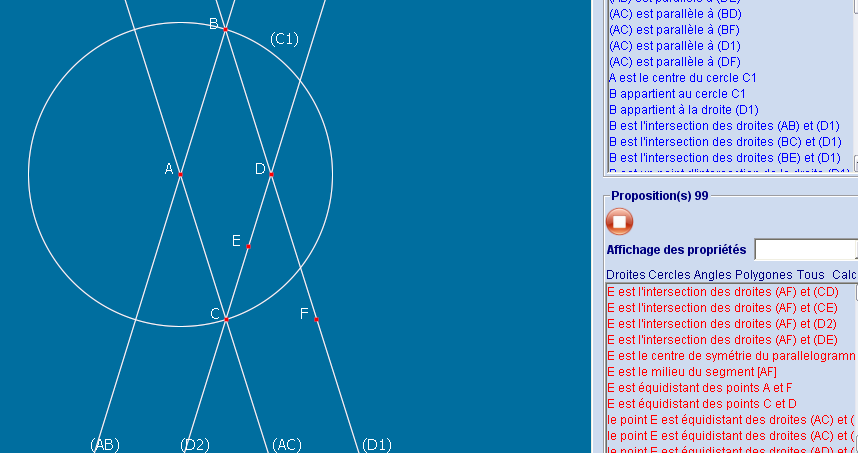
Dès que E (milieu de [CD]) et F (symétrique de B par rapport à D) sont construits, Géométrix affiche (en bas à droite) que E est le milieu de [AF] :

(incidemment, une piste de démonstration apparaît juste au-dessus...). Pour avoir une démonstration automatique, on doit cliquer sur l’icône représentant un professeur et paramétrer le moteur d’inférence. La première entrée du menu permet de définir des restrictions (choisir des axiomes pour démontrer au niveau voulu, avec les outils connus des élèves de ce niveau) :

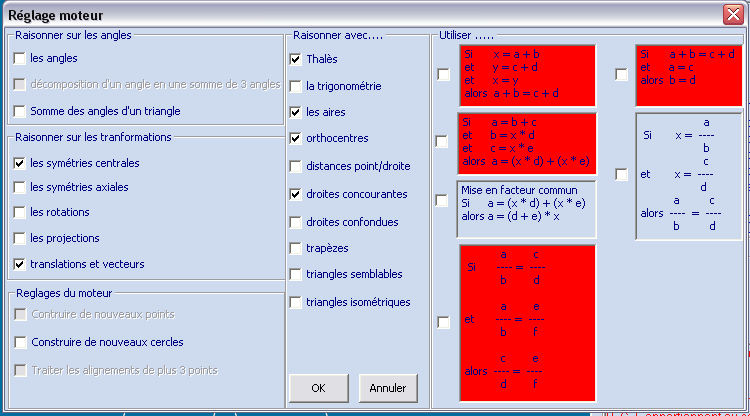
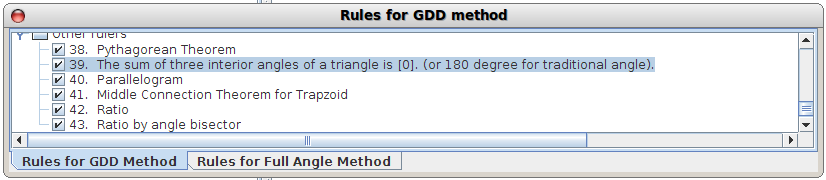
L’onglet « base de théorèmes » permet de choisir les théorèmes utilisables dans la démonstration à venir :

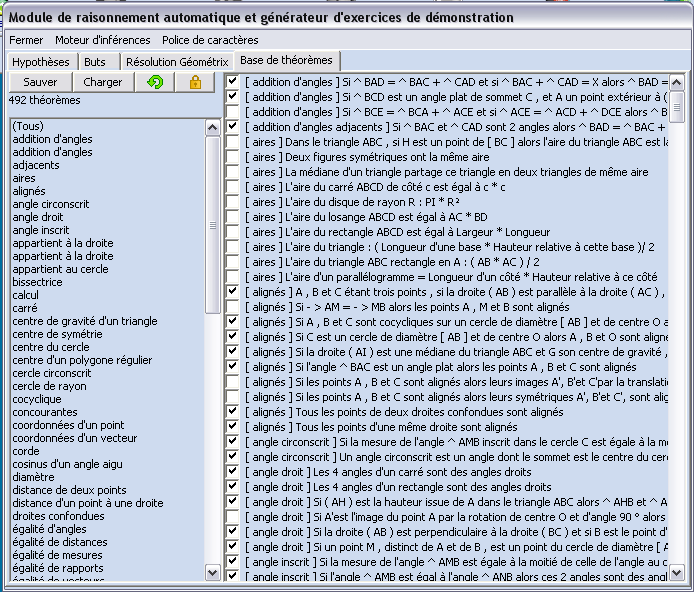
(hélas, il n’est pour l’instant pas possible de désactiver les axiomes d’Euclide et de Desargues pour explorer les géométries non euclidienne et non arguésienne ; qui a dit « tant mieux » ?). L’onglet « but » permet de choisir parmi les centaines de propositions trouvées par Géométrix, celle qu’on veut démontrer. En cliquant dessus (par exemple en l’activant), on voit la démonstration à droite de l’écran :

Plus précisément, il ramène la preuve de la conjecture à des preuves d’autres conjectures (ou « tactiques » dans le langage de Coq). Dans le cas présent, on peut traduire par « si seulement je pouvais prouver que ACFD est un parallélogramme alors comme E est déjà le milieu de la diagonale [CD], on aurait prouvé que E est aussi le milieu de l’autre diagonale ». La démonstration est alors ramenée à celle d’une autre conjecture, qu’on peut explorer en cliquant dessus dans la liste des buts possibles. Ce qui permet récursivement d’arriver à devoir démontrer des hypothèses, ce qui achève l’exercice.

JGex est un logiciel similaire à Géométrix, mais développé en Java, donc multiplateforme. L’histoire remonte apparemment à Wu Wenjun qui a découvert un algorithme pour démontrer des théorèmes analytiquement (voir ci-dessous la démonstration par le calcul) qui ressemble beaucoup à l’algorithme d’Euclide. Des étudiants, sans doute sous son impulsion, ont travaillé sur un logiciel mettant en pratique l’algorithme de Wu, et dont le nom anglais est Geometry Expert. Lors d’un séjour au Canada, ils ont réalisé JGex qui est la version Java de Gex. Puis apparemment ils sont retournés en Chine où ils ont recommencé leur travail avec le nouveau logiciel MMP, entièrement en Mandarin, et non libre. D’ailleurs JGex non plus n’est pas libre. Il n’empêche que c’est un beau logiciel (mais ses auteurs ont une orthographe anglaise très hésitante...).

Le losange n’existant pas dans le vocabulaire de JGex, on est obligé de construire un cercle. Chaque étape de la construction est ponctuée par une mise à jour de la liste des faits à gauche de la figure. Quand celle-ci est construite, on peut choisir dans le menu « to prove » le fait à prouver (ici « midpoint », en sélectionnant dans un menu déroulant les noms des points F, A et E) ; immédiatement, JGex répond que la proposition est vraie :

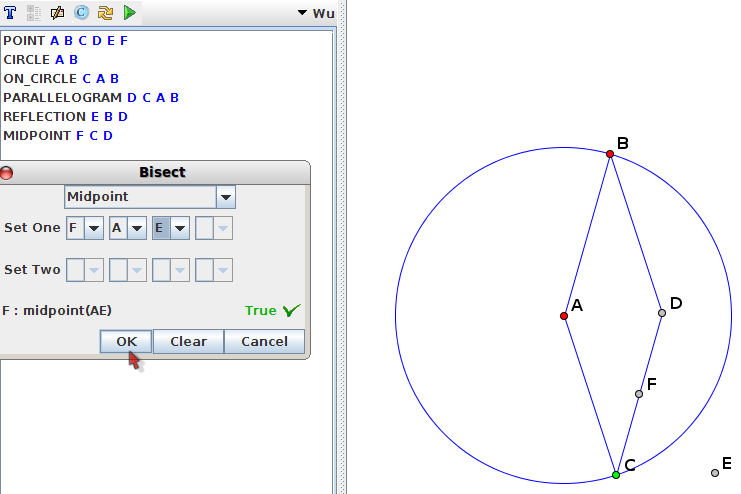
Ci-dessus, l’algorithme de Wu est sélectionné pour la démonstration (voir ci-dessous le résultat surprenant qu’il donne) ; en sélectionnant la déduction « GDD », on obtient automatiquement la démonstration suivante :

Comme là encore, on a une arborescence de tactiques, on lit mieux la démonstration de bas en haut :

• point10 : BD=DE par hypothèse sur E ;
• point 9 : F est équidistant de C et D par construction
• point8 : le parallélisme entre (AC) et (BD) entraîne une égalité d’angles alternes-internes ;
• point 7 : Les longueurs AC et BD, toutes deux égales à DE, sont égales entre elles ;
• point 5 : D’après les points 7, 8 et 9, les triangles CFA et DFE sont isométriques (en fait l’isométrie en question est une symétrie centrale ce qui évite d’avoir à utiliser ce vocabulaire d’« égalité des triangles »).
• Donc (point 6), on a deux angles (opposés par le sommet) égaux entre eux ;
• Point 4 : donc les droites (FA) et (EF) sont parallèles (les angles pouvant être considérés comme alternes-internes) ;
• Point 3 : D’après le point 5, FA=FE (la symétrie centrale conserve les longueurs).
• Point 2 : Deux droites parallèles entre elles ayant un point commun sont confondues : F, A et E sont alignés
• Enfin, point 1 : Les points 2 et 3 se résument à la propriété de milieu conjecturée.

La démonstration est plus compliquée que celle de Géométrix (plus longue, et utilise les triangles isométriques, ce qui n’était pas nécessaire). Mais il suffit de cliquer sur une proposition pour la voir codée sur la figure, avec une animation, et un lien vers la règle utilisée pour démontrer la propriété :

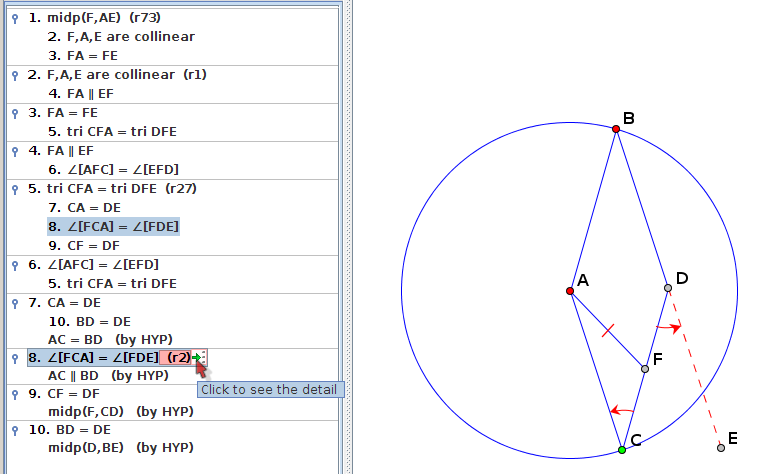
En cliquant sur « lemmas », on peut voir la liste des règles des axiomes utilisables pour la démonstration, parmi lesquels on retrouve l’axiome d’Euclide :

Las ! Malgré ce que laisse penser la présence d’une case à cocher, il est impossible de désélectionner un axiome, donc là aussi, les géométries non euclidiennes et non arguésienne sont exclues de JGex [2]...

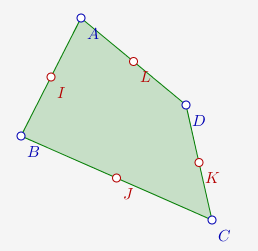
Le logiciel DrGeoII est écrit en Smalltalk, un langage objet d’âge similaire à celui de Prolog, et depuis des années, des tentatives pour l’interfacer avec Prolog ont été menées, y compris avec un Prolog écrit en Smalltalk. En ce moment, l’idée la plus aboutie est celle d’un système expert écrit directement en Smalltalk. Ce système expert a déjà été interfacé avec DrGeoII, mais pour démontrer autre chose que le théorème de Varignon montré dans l’exemple, il reste encore à enrichir ce système avec une collection d’axiomes plus impressionante, ce qui risque d’être long et de nécessiter de l’aide, pour l’instant encore attendue...

Mais cette possibilité d’extraire des données logiques d’une figure géométrique est déjà impressionnante, d’autant que contrairement aux logiciels précédents, la manière de faire est accessible à la lecture (dans le langage Smalltalk), les logiciels Pharo et DrGeoII étant libres.

Et puis, comme la base d’axiomes est éditable avec un fichier texte, on peut y mettre les axiomes qu’on veut, et donc explorer les géométries non arguésienne et non euclidiennes de manière purement axiomatique...

En fait, le mode de fonctionnement de ces logiciels ressemble à celui de l’apprentissage : On part d’une base de connaissance (les axiomes) et on l’enrichit par déduction ; la base de connaissance grandit alors jusqu’à ce qu’on arrive à y trouver la proposition à prouver. Or il existe une théorie de la connaissance, c’est la logique épistémique. Son axiome de la connaissance $Kp \Rightarrow p$ empêche le droit à l’erreur (il se traduit par « si je sais que p est vraie, alors p ne peut pas être fausse ») ; c’est lui qui est responsable du fait qu’au cours du temps, la quantité de connaissance ne peut que croître.

Or l’intelligence ne se réduit pas à la connaissance, et se caractérise plutôt par la possibilité de remettre en question les fondements même de la connaissance (comme dit l’expression « détruire pour mieux reconstruire ») ; on a donc cherché à remplacer la logique épistémique par la logique doxastique, ou logique des croyances. La logique doxastique est une logique non monotone, qui permet la révision de croyances (on peut supprimer un fait lorsqu’on s’aperçoit que finalement on n’y croit plus, comme les coups de gomme du Sudoku quand on dit « ah ben non ça ne peut pas être un 6 finalement »).

Le cours de psychologie cognitive expérimentale de Stanislas Dehaene laisse penser que le cerveau humain (même celui du nourrisson) est structuré de manière à pratiquer l’inférence bayésienne (avec ses révisions de connaissances) plutôt que le raisonnement déductif.

Le problème P = NP quant à lui, suggère que l’intervention de l’intuition [3] (ou « trait de génie » ou « haha » comme l’appelait Martin Gardner) peut être nécessaire, par manque de temps pour l’exhaustivité du raisonnement, bien plus souvent qu’on le voudrait. En d’autres termes, certains problèmes sont peut-être tout simplement trop difficiles pour se prêter à des démonstrations par syllogismes. On peut donc s’attendre à une recrudescence des preuves probabilistes ou constructivistes dans l’avenir.

La logique intuitionniste privilégie la démonstration constructive dont un aspect important est la preuve par le calcul : Quand on demande de « démontrer que f’(x)=(2x+1)(5-x) », on attend bien un calcul et pas un syllogisme.

La logique intuitionniste refuse

1. le tiers exclu
2. la démonstration par l’absurde
3. l’utilisation de l’infini potentiel

Ceci dit, pour démontrer que 32 est pair, il suffit d’effectuer la division de 32 par 2 et de constater que le quotient est entier. Il y a donc quelque chose de très concret dans la logique intuitionniste.

Le logiciel JGex décrit ci-dessus permet de démontrer des théorèmes, non seulement à l’aide de moteurs d’inférence, mais aussi par le calcul formel. L’idée est de représenter chaque hypothèse par une condition algébrique, ce qui définit l’espace des propositions comme l’intersection de variétés algébriques, et enfin, démontrer que la condition algébrique qui exprime la conclusion à prouver, se ramène à un calcul algébrique. C’est l’algorithme de résolution algébrique qui diffère selon la méthode employée : Bases de Grobner, ou algorithme de Wu. JGex permet de choisir entre les deux, et ses auteurs affirment que le nombre de propositions démontrées par JGex avec l’algorithme de Wu dépasse largement celui des propositions démontrées par les bases de Grobner, et encore plus celui des propositions démontrées déductivement. En général...

Un exemple

Pour démontrer le théorème de Varignon, on peut choisir son repère de telle manière que l’espace soit de dimension deux (s’il y avait un cercle dans la construction, on aurait besoin d’un repère orthonormé ce qui amènerait à un espace de dimension 4 ou plus).

Pour montrer que IJKL ci-dessus est un parallélogramme, on peut choisir le repère affine que l’on souhaite puisque toutes les propriétés de la figure sont elles-mêmes affines, et en choisissant pour repère (B,A,C), on a les coordonnées suivantes : A(0,1), B(0,0), C(1,0), I(0,1/2) et J(1/2,0). Alors, en appelant (a,b) les coordonnées de D,

• L’hypothèse « K(c,d) est le milieu de [CD] » se traduit par les équations 2c=1+a et 2d=b ;
• L’hypothèse « L(e,f) est le milieu de [DA] » se traduit par les équations 2 e=a et 2f=b+1 ;

En résumé, dans l’espace de dimension 6 engendré par a, b, c, d, e et f, chaque équation (qui est linéaire dans le cas présent) restreint l’espace des configurations possibles à un hyperplan (de dimension 5), et l’intersection de deux hyperplans étant en général de dimension moindre (4), on se demande si les conditions affirmant que IJKL est un parallélogramme sont systématiquement dans cet espace. Dans le cas présent, comme le vecteur allant de I à J est de coordonnées (1/2,-1/2), et celles du vecteur allant de L à K sont (c-e,d-f), les conditions qui expriment que IJKL est un parallélogramme sont

1. 2(c-e)=1 ;
2. 2(d-f)=-1.

Alors la démonstration du théorème de Varignon revient à montrer que l’espace engendré par ces deux conditions (de dimension 4) est inclus dans l’espace de dimension 4 précédent. Ce qui se fait algébriquement (et facilement dans le cas présent, il suffit de calculer les coordonnées des vecteurs en fonction de a et b). Et même pour des propositions euclidiennes (concernant des angles et des cercles) le système, non nécessairement linéaire, reste soluble par le calcul formel, comme le montrent les deux onglets suivants.

Bien que JGex sache prouver que E est le milieu de [AF] avec la méthode déductive, la méthode de Wu échoue dans ce cas :

Par exemple, le point 4 donne deux équations exprimant que F est le milieu de [CD] (visiblement, les variables x11 et x12 sont les coordonnées de F) ; les équations h0 à h6 viennent d’une triangulation du système ; la suite des restes des divisions de l’algorithme d’Euclide apparaît en bas de la figure, et le dernier de ces restes n’étant pas nul, la proposition n’est pas considérée comme démontrée. En affichant le message selon lequel la proposition est fausse (alors que JGex l’affichait comme vraie), le logiciel permet de cliquer sur un bouton pour afficher le reste non nul en question.

Bien entendu, c’est vraisemblablement un bogue (une erreur de calcul formel) qui est responsable de cette affirmation erronée. Le calcul formel permet bel et bien de démontrer la proposition.

Xcas permet de faire la figure pour conjecturer la propriété (en géométrie dynamique) mais alors, on est dans un monde numérique où les calculs sont approchés, et non dans le monde formel qui permet de prouver réellement la propriété conjecturée. Pour cela, on peut choisir un point de coordonnées (x,y) pour A et deux points B et C sur le cercle de centre A et de rayon 5 (pour avoir moins d’inconnues à l’affichage). Pour éviter d’allonger à l’excès les équations, on peut fixer, sans perte de généralité, C à la verticale de B (lignes 1 à 3 ci-dessous) :

La ligne 4 montre la syntaxe pour compléter un parallélogramme ; la ligne 5, celle du milieu, et la ligne 6, celle du symétrique. Pour terminer la démonstration que O est le milieu de [AP], on peut créer le milieu en question (Q à la ligne 7) et vérifier que ses coordonnées (formelles) sont les mêmes que celles de O, par exemple en demandant à Xcas (ligne 8) de calculer les coordonnées du vecteur allant de O à Q.

En fait, dans tout cet exercice, le fait que ABDC est un losange est un distracteur. La proposition à démontrer est affine, et seul le parallélogramme est utile à la démonstration. On peut donc « démontrer par le calcul » en choisissant pour repère (A,B,C). Alors A(0,0), B(1,0) et C(0,1). L’hypothèse « ABDC est un parallélogramme » donne les coordonnées de D(1,1). Et l’hypothèse « E est le milieu de [CD] » donne les coordonnées de E(1/2,1). Enfin, l’hypothèse « B’ est le symétrique de B par rapport à D » donne les coordonnées de B’(1,2). Ces coordonnées permettent de calculer dans le repère (A,B,C) les coordonnées du milieu de [AB’] et de vérifier que c’est bien E.

Alternativement, on peut utiliser le repère orthonormé de GeoGebra (en arguant du fait que la proposition est affine) et laisser ce dernier calculer les coordonnées des points de la figure :

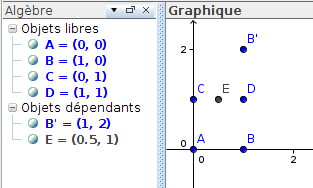
Ensuite, il suffit de rajouter le symétrique de A par rapport à E (que GeoGebra nomme A’) et de constater qu’il a les mêmes coordonnées que B’. En cas de doute, on peut utiliser l’outil « relation entre objets » de GeoGebra qui confirme l’égalité des deux points :

Les mathématiques constructives sont mises à mal par ces constatations, la notion de « prouver, c’est construire » devenant progressivement celle de « prouver, c’est dire qu’on pourrait construire », et la construction elle-même se défosse sur l’ordinateur. Depuis la démonstration du théorème des quatre couleurs par ordinateur, les exemples se multiplient, où l’étape la plus longue de la démonstration se fait avec un ordinateur, parce que sa longueur la rend inaccessible à l’être humain (conjecture de Kepler, de Seifert ...). Peu de gens ont pris la peine de lire les centaines de pages qui démontrent que la classification des groupes simples sporadiques est terminée, mais tout le monde fait confiance à ceux qui ont rédigé ces pages (même si certains passages sont peut-être plus évoqués que démontrés [6]) ainsi qu’à Andrew Wiles et Grigory Perelman, qui sont plus faillibles qu’un ordinateur, mais on est de plus en plus amené à faire confiance à l’ordinateur parce qu’on ne peut pas faire autrement. Ce qui pose des problèmes nouveaux et parfois très terre-à-terre :

• L’importance épistémologique des logiciels libres (on a encore moins confiance en l’ordinateur si on est privé de la possibilité théorique de vérifier son travail)
• la nécessité d’accepter l’utilisation quotidienne de résultats non constructifs : Bien qu’on ne sache pas s’il existe un algorithme factorisant rapidement des nombres entiers, on utilise RSA pour les échanges bancaires, et on n’a pas la certitude que RSA est sûr, ni qu’on aura cette certitude un jour
• Le manque de temps laisse la part belle à l’émission de conjectures et le cours de maths ressemble de plus en plus à une liste d’algorithmes (ce qu’il était d’ailleurs à ses débuts avec les ouvrages d’Âryabhata et al Khawarizmi)

Pour montrer que le point rouge ci-dessous est bien le symétrique de A par rapport au point marron, CaRMetal utilise une méthode fréquentielle (déjà existante chez Cinderella) consistant à secouer la figure dans tous les sens pour estimer la proportion de cas où la proposition est fausse, à l’aide de l’outil de validation de conjecture appelé Monkey et déjà utilisé au premier cycle. La construction de la figure est assez rapide avec l’outil « translation » :

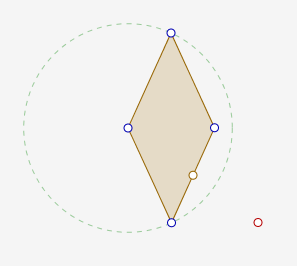
Pour valider l’hypothèse, on peut construire le symétrique de A par rapport au point marron et le comparer avec le point rouge, en actionnant le Monkey pour vérifier que le résultat du test ne change pas.

Mais une alternative est de créer un exercice pour automatiser ce test : Il suffit de demander la construction du point rouge comme énoncé de l’exercice, et de laisser l’outil « symétrique » disponible pour faire l’exercice « en trichant » [7].

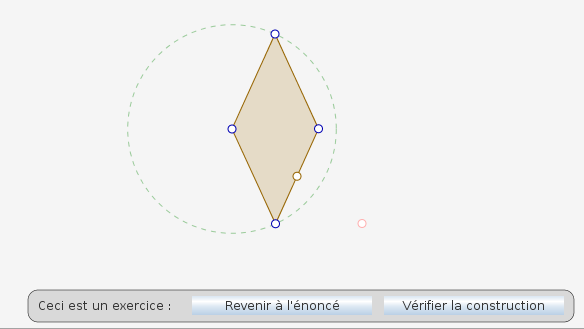
Après ça, en cliquant sur « vérifier la construction », une barre de progression s’affiche et au bout de quelque temps, le pourcentage de cas de figure où la proposition est vraie apparaît (ou plutôt, n’apparaît pas puisqu’il est égal à 100%) :

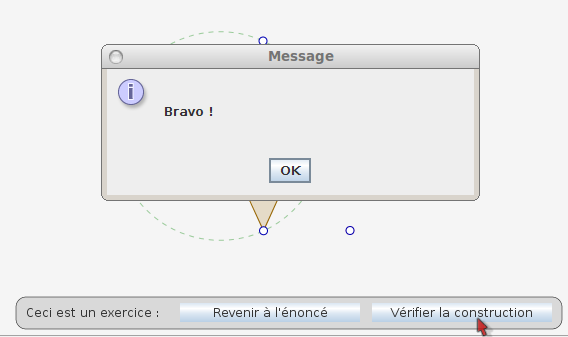
Fermat dirait « j’ai exclu une si grande quantité de cas de non-alignement que j’aurais peine à me déduire » !

Lorsqu’on demande à l’ordinateur si 12345678901234567891 est premier, il répond « probablement oui ». Le principe est de vérifier le petit théorème de Fermat sur des exemples. Par exemple, avec DrGeoII, le test de primalité de Miller-Rabin est utilisé :

Comme on estime la proportion de résultats faussement positifs inférieure à 0,25, et qu’on fait le test sur 25 valeurs indépendantes (enfin théoriquement) entre elles, on estime la probabilité que 12345678901234567891 soit composé à $0,25^{25}\simeq 8,9 \times10^{-16}$ qui est négligeable. En Java par exemple, le test de primalité est nommé isProbablePrime et ne donne la primalité qu’à une probabilité donnée près, laquelle est aussi proche de 1 qu’on le souhaite, mais au prix d’un temps accru à passer dessus...

Si on accepte de faire ainsi (est-ce encore des maths ?) c’est encore une fois parce qu’on n’a pas vraiment d’autre choix, mais aussi parce qu’on estime que la probabilité d’apparition d’un bogue est largement supérieure à $10^{-15}$.

Lorsqu’Xcas prétend que 12345678901234567891 est premier, il ne paraît pas raisonnable de mettre en doute cette affirmation ; d’autant que ce logiciel étant libre, on peut voir comment il trouve que 12345678901234567891 est premier, en consultant la partie du code source qui se charge des tests de primalité. Mais lorsque Fermat affirmait que 4294967297 était premier, même si Fermat lui-même présentait ce résultat comme une conjecture qu’il restait à vérifier, on voit bien (depuis Euler) qu’il fallait émettre un doute sur cette conjecture.

Avant même de lire une démonstration abordable du théorème de Morley, j’avais personnellement confiance en ce résultat : C’est un théorème qui a été démontré par quelqu’un qui a l’air digne de confiance et « on voit bien » avec un logiciel de géométrie dynamique que c’est vrai. Or c’est bien par l’émission de conjectures qu’on fait découvrir les théorèmes de géométrie plane, et ceux-ci sont de plus en plus souvent admis (et présentés comme tels). Une situation analogue s’est récemment présentée avec le théorème d’Ayme dont une courte démonstration par le calcul formel a été donnée sur wikipedia anglais (en utilisant une de ces fameuses « propriétés bien connues » que je ne connaissais pas...).

Admettre un résultat sans démonstration, juste parce qu’il a l’air vrai (et l’ordinateur semble le confirmer) est pratique en cours de maths (pour aller plus vite, au risque de frustrer les meilleurs élèves). De toute manière, il est difficile de rédiger une démonstration vraiment exhaustive (quels sont les axiomes, faut-il démontrer tous les résultats intermédiaires, même ceux qui paraissent évidents ?). Les « ROC » du bac S sont des démonstrations courtes dont les hypothèses sont clairement rappelées, et portent le plus souvent sur d’autres domaines que la géométrie (typiquement, analyse ou arithmétique).