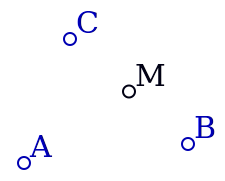
On construit donc trois points A, B et C [1] sur la figure :

Pour construire le milieu M de [BC], il n’y a pas besoin de construire le segment [BC], puisque le point B possède aussi l’outil milieu :

Outil à faire glisser vers C :

Ensuite c’est plus difficile puisqu’on veut construire D tel que M est milieu de [AD]. Spécialement pour les élèves qui souhaitent utiliser cet article pour tricher en TP, nous ne dirons pas comment faire ; disons simplement que DGPad a un outil pour cela, et que c’est au point M qu’on va l’appliquer :

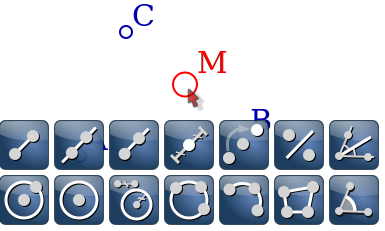
Pour mieux distinguer les objets initiaux de l’objet final (le point D), on peut les colorier différemment :

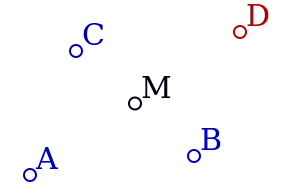
Pour créer une macro, on sélectionne l’outil adéquat :

En sélectionnant le point A (comme objet initial) celui-ci est mis en exergue, et son nom apparaît automatiquement dans la liste des initiaux :

Lorsqu’on a sélectionné B et C, les points M et D sont également mis en exergue, mais dans une couleur différente : Ce sont des candidats à être objets finaux de la macro :

Cependant, M est juste un objet intermédiaire de la macro, on ne sélectionne donc que D, ce qui fait de la macro une transformation ponctuelle :

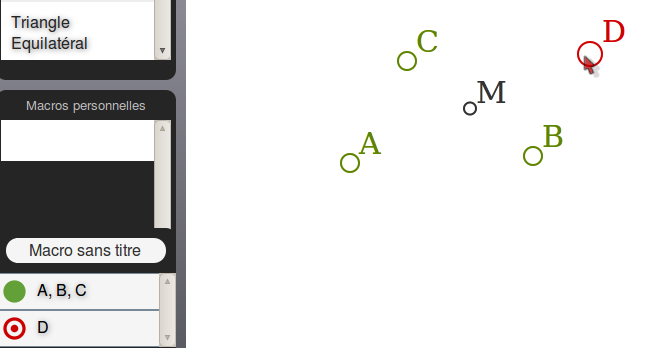
Il ne reste maintenant plus qu’à nommer la macro :

Distribution

Si on enlève de la figure les points A, B et C, M et D disparaitront aussi, mais pas la macro. En enregistrant le résultat comme une figure DGPad, celle-ci permettra donc d’appliquer des translations simplement en utilisant la macro (origine du vecteur d’abord, puis extrémité, puis le point à translater). Le contenu du fichier est du JavaScript :

On y apprend que $macros est un objet de DGpad (un tableau JavaScript), initialement vide [2] ; qu’à la page « translation », se trouvent deux propriétés et une fonction :

1. La propriété name est une chaîne de caractères, accessible par $macros[« translation »].name ;
2. la propriété parameters est un tableau de chaînes de caractères, signifiant que les trois initiaux sont des points ;
3. la fonction exec a trois antécédents, notés A, B et C, et s’exécute avec $macros[« translation »].exec(O,I,P) si on veut appliquer au point P la translation qui envoie O sur I [3]. La fonction exec renvoie un tableau contenant les noms des objets finaux (ici seul le point D).

Cette notation avec des points peut paraître compliquée, mais elle permet à chaque macro d’avoir sa propre fonction exec.

Voici la version copiable-collable (l’original est téléchargeable en bas de l’article) :

// Macros :
$macros={};
$macros["translation"]={
	name:"translation",
	parameters:["point","point","point"],
	exec:
	function (A,B,C){
M=MidPoint("M",B,C);
D=Symmetry("D",M,A);
return [D];
}};

Voici la figure avec macro :

Dans la figure ci-dessous, les points bleus sont libres dans le plan, et les points rouges sont leurs translatés (les points A et B, en vert, désignant le vecteur) :

En manipulant cette figure, on vérifie que la translation conserve les longueurs [4].

Il résulte de la réciproque du théorème de Pythagore, qu’une translation conserve également les angles :

On démarre la figure avec la macro translation et on y ajoute, comme précédemment, les points A, B et deux autres points libres :

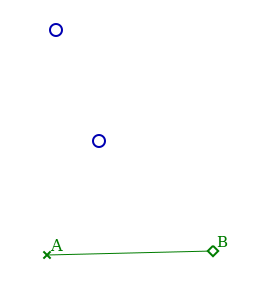
Mais plutôt que se concentrer sur leurs translatés, on les joint par une droite :

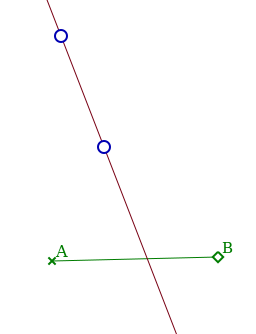
En sélectionnant cette droite, on peut y attacher un point :

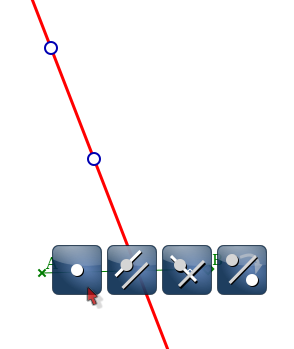
Le voici en noir :

On définit le translaté de la droite comme le lieu des translatés du point noir ; on construit donc ce translaté (en rouge, avec la macro) :

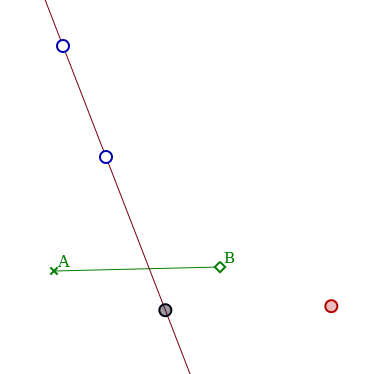
Puisqu’il est l’image d’un point lié par la translation, ce point possède maintenant un outil lieu :

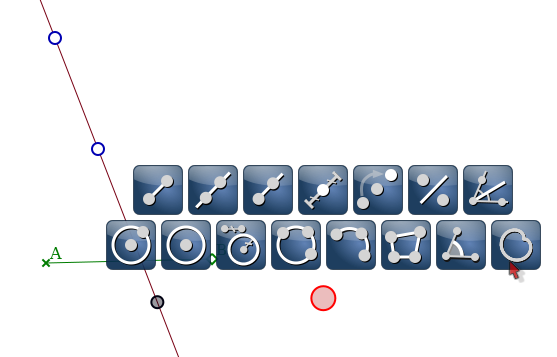
En l’appliquant, on a l’image de la droite par la translation :

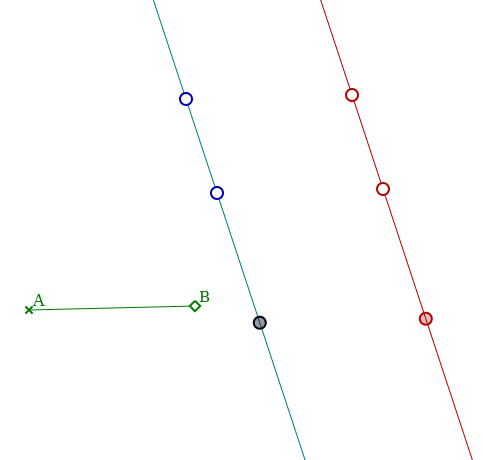
Ce qui permet de conjecturer

• que l’image d’une droite est une droite ;
• qu’en plus elle est parallèle à la droite de départ
• qu’en plus elle passe par les translatés des points qui définissent la droite...

Application

Une fois admises les conjectures précédentes [5], on peut donc construire l’image d’une droite par une translation :

• on place sur la droite deux points mobiles (il faut que les points dépendent de la droite et non l’inverse) ;
• on construit les images de ces deux points par translation ;
• on joint les images en question par une droite.

Cette construction peut être convertie en une macro ayant A, B et la droite comme initiaux, et la droite translatée comme objet final :

Un exemple montrant un segment et son translaté se trouve dans l’onglet « isométrie » ; on y voit non seulement que le translaté d’un segment a la même longueur que celui-ci, mais aussi que ledit translaté est parallèle au segment de départ. Ce qui est d’ailleurs la conséquence de l’onglet précédent.

Du fait que la translation conserve les longueurs, on déduit que

• le translaté d’un triangle isocèle est isocèle
• le translaté d’un triangle équilatéral est équilatéral
• le translaté d’un triangle rectangle est rectangle

On peut vérifier ces conjectures en manipulant le triangle bleu ci-dessous :

Mais comme ce sont des propriétés obtenues par déduction, on peut aussi les donner en devoir maison après le cours, et si on a un peu de temps, le réserver à l’étude des translatés de cercles :

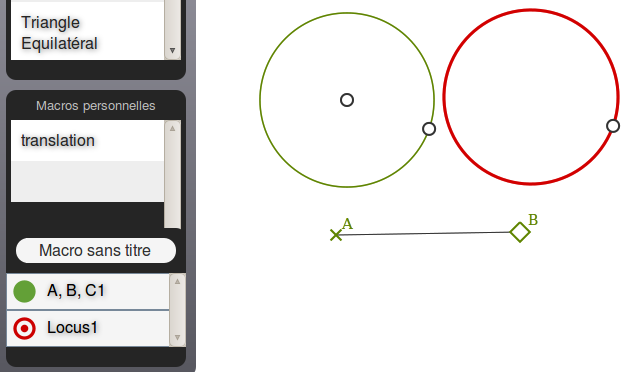
Sur la figure habituelle avec A et B (et la macro « translation »), on construit un cercle (par exemple, ici, de rayon fixe) :

Si on sélectionne ce cercle, on peut y attacher un point :

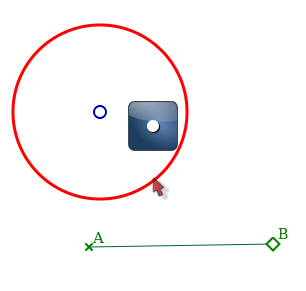
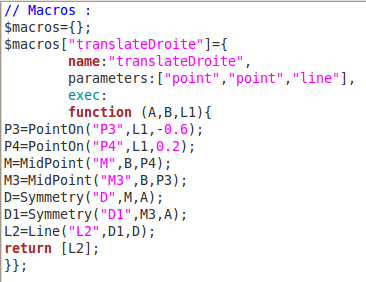
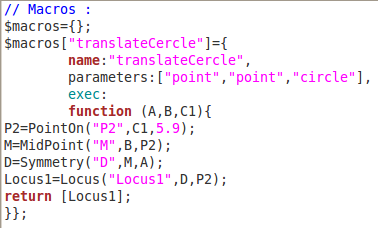
Le translaté du cercle étant défini comme le lieu des translatés de ce point, on utilise donc la macro « translation » pour construire le translaté en question (avec choix de A puis de B puis du point sur cercle) :

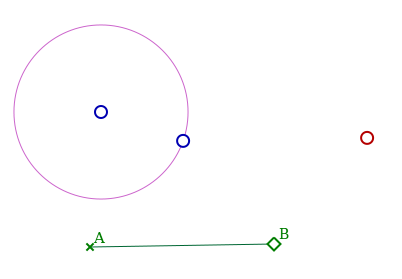
Ce-dessus le translaté a été colorié en rouge pour le distinguer des autres points ; comme ce point dépend d’un point sur cercle, il possède un outil lieu :

Le lieu apparaît alors en rouge sombre :

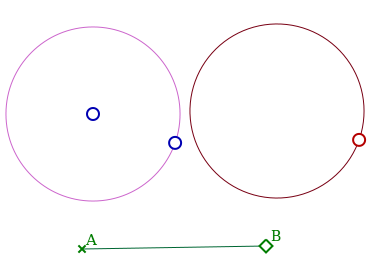
On peut alors conjecturer

• que le translaté d’un cercle est un cercle ;
• qu’en plus, il a le même rayon que le cercle initial ;
• qu’en plus (en construisant son centre), son centre est le translaté du centre du cercle de départ...

nouvelle macro

Si en mode de création de macro, on sélectionne comme objets initiaux, les points A, B et le cercle de départ :

on voit qu’il est possible de choisir le lieu comme objet final ; en le faisant on a une macro construisant l’image d’un cercle par translation :

Voici le source de cette macro :

Toutefois, le translaté d’un cercle n’est pas un cercle mais un lieu ; pour avoir un cercle, il faut d’abord construire le centre du cercle à partir du cercle lui-même ; cette construction est laissée en exercice (indication : On peut attacher d’autres points au cercle).

En affichant les axes de DGPad, on peut conjecturer le lien entre les coordonnées de points liés par une translation, et s’approprier la notion de coordonnées de vecteurs :

Pour mieux y voir, on peut attacher l’origine de l’un des représentants du vecteur à l’intersection des deux axes :

Cette figure permet d’ailleurs de vérifier expérimentalement que les coordonnées du vecteur allant de O à M sont les mêmes que les coordonnées de M...

Les boucles de JavaScript permettent d’itérer une ou plusieurs translations et donc de construire des frises et pavages

Algorithme pour une frise

• on part de trois points d, e et f ;
• on leur applique la translation allant de A à B ;
• on joint les nouveaux points d, e et f par un triangle
• on répète le tout dans une boucle.

// Macros :
$macros={};
$macros["translation"]={
	name:"translation",
	parameters:["point","point","point"],
	exec:
	function (A,B,C){
M=MidPoint("M",B,C);
STL(M,"h:1");
D=Symmetry("D",M,A);
return [D];
}};

a=Point("A",-5,-1);
STL(a,"c:#00aa00;s:3;sp:1");
b=Point("B",-3,-1);
STL(b,"c:#00aa00;s:3;sp:2");
S1=Segment("S1",a,b);
STL(S1,"c:#00aa00");
P3=Point("P3",-7,0);
P4=Point("P4",-6,2);
P5=Point("P5",-4,1);
Tri0=Polygon("Tri0","_P3,_P4,_P5");
STL(Tri1,"o:0.2");
[d,e,f]=["P3","P4","P5"];
for(n=1; n<20; n++){
	d=$macros["translation"].exec("A","B",d);
	STL(d,"h:1");
	e=$macros["translation"].exec("A","B",e);
	STL(e,"h:1");
	f=$macros["translation"].exec("A","B",f);
	STL(f,"h:1");
	t=Polygon("Tri"+n,"_d,_e,_f");
}

La frise obtenue est dynamique :

Algorithme pour un pavage

On rajoute un troisième point C :

• On fait comme une frise, en itérant la translation allant de A à C ;
• à chaque fois, on construit une frise en itérant la translation allant de A à B, sur le triangle obtenu.

// Macros :
$macros={};
$macros["translation"]={
	name:"translation",
	parameters:["point","point","point"],
	exec:
	function (A,B,C){
M=MidPoint("M",B,C);
STL(M,"h:1");
D=Symmetry("D",M,A);
return [D];
}};

a=Point("A",-5,-1);
STL(a,"c:#00aa00;s:3;sp:1");
b=Point("B",-3,-1);
STL(b,"c:#00aa00;s:3;sp:2");
c=Point("C",-4.9,-0.5);
STL(c,"c:#00aa00;s:3");
S1=Segment("S1",a,b);
STL(S1,"c:#00aa00");
S2=Segment("S2",a,c);
STL(S2,"c:#00aa00");
P3=Point("P3",-7,0);
P4=Point("P4",-6,2);
P5=Point("P5",-4,1);
Tri0=Polygon("Tri0","_P3,_P4,_P5");
STL(Tri0,"o:0.2");
[d,e,f]=["P3","P4","P5"];
for(n=1; n<16; n++){
	d=$macros["translation"].exec("A","B",d);
	STL(d,"h:1");
	e=$macros["translation"].exec("A","B",e);
	STL(e,"h:1");
	f=$macros["translation"].exec("A","B",f);
	STL(f,"h:1");
	t=Polygon("Tri"+n,d+","+e+","+f);
}
[d,e,f]=["P3","P4","P5"];
for(m=1; m<12; m++){
	d=$macros["translation"].exec("A","C",d);
	STL(d,"h:1");
	e=$macros["translation"].exec("A","C",e);
	STL(e,"h:1");
	f=$macros["translation"].exec("A","C",f);
	STL(f,"h:1");
	t=Polygon("Tr"+m+"0",d+","+e+","+f);
	[g,h,i]=[d,e,f];
	for(n=1; n<16; n++){
		g=$macros["translation"].exec("A","B",g);
		STL(g,"h:1");
		h=$macros["translation"].exec("A","B",h);
		STL(h,"h:1");
		i=$macros["translation"].exec("A","B",i);
		STL(i,"h:1");
		t=Polygon("Tr"+m+"x"+n,g+","+h+","+i);
	}
}

Le pavage est un peu lourd à ouvrir :

En faisant « glisser » un segment de DGPad, on applique une translation ; ceci aussi aide à appréhender le fonctionnement de cette transformation.

Le fait qu’il est possible d’aller de plusieurs manières d’un point à un autre (par plusieurs trajets) illustre la commutativité de la composition des translations. Ceci permet de définir l’addition des vecteurs. Toutefois, bien que ce ne soit pas au programme, on peut aussi définir l’addition des vecteurs avec les coordonnées.