Le colloque des 20 ans de Repères IREM a déjà été présenté par Alain Busser à travers cet article-blog. Même si localement on ne peux pas dire que nous soyons des « endormis », les animateurs IREM de la Réunion sont en définitive bien éloignés de la vie foisonnante des relations inter-IREM. Nous avions eu un premier aperçu de cette richesse lors de la semaine des 10 ans de notre IREM (décembre 2009), où plusieurs conférenciers sont venus de différents IREM, avec en particulier un stage de logique animé par René Cori qui s’avère être aussi l’un des deux organisateurs du colloque à Luminy, et aussi celui qui avait pensé et réussi à ce que ce colloque ait lieu au CIRM.
En plus de Dominique Tournès, présent comme intervenant et directeur d’IREM, nous étions donc deux animateurs de La Réunion participant à ce colloque, essentiellement à cause de l’atelier sur les CaRScripts. La participation à un tel colloque, en un tel lieu, est déjà en soi un cadeau. On y croise des auditeurs qui ont construit les IREM, des participants de toutes horizons mathématiques, des intervenants aussi prestigieux que Jean Pierre Kahane. Bref on y croise ceux qui ont marqués de leurs réflexions ou de leurs pratiques, d’une façon ou d’une autre, les 40 dernières années de l’enseignement des mathématiques en France.
Alors bien sûr, il vient une heure où il faut aussi aller face à ce type de public ... pas vraiment facile, mais bon, si c’est pour faire connaître un peu plus CaRMetal ... Il suffit d’arriver à ravaler ses questions existentielles sur d’éventuelles erreurs de casting, puis de commencer, le temps s’occupe ensuite du reste. Alors allons-y.
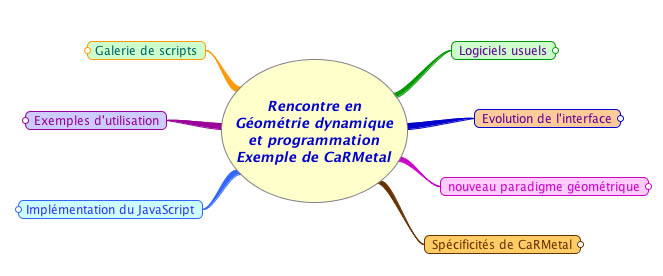
Techniquement le texte préparé pour ce compte rendu ne tenant pas dans un seul article SPIP, il est partagé en deux partie, la première sur l’usage standard de CaRMetal, principalement en géométrie d’ailleurs (partie droite de la carte), la seconde sur les Carscripts (partie gauche). Ce compte rendu va plus loin dans ses développements que ne le permettait une présentation en 1 h 15. C’est pour cela qu’il est découpé en plusieurs chapitres sous forme d’onglets.
Organisation de la lecture/navigation
Le site de l’IREM de La Réunion contenant déjà de nombreux articles sur CaRMetal, généralement avec des applets, pour un accés plus rapide, cette présentation-ci ne propose que des copies d’écran. Nous renvoyons aux articles antérieurs pour aller plus dans les détails techniques.
Même si elles sont abondamment illustrées d’exemples, ces pages restent centrées sur une analyse des possibilités du logiciel en particulier en terme d’évolution des pratiques. Chacun peut télécharger les classeurs associés à cette présentation en fin d’article, soit encore tester le logiciel et les figures en ligne.
Dans la seconde partie sur les scripts, des compilations d’articles précédents sont aussi proposées en fin d’article.
Intro
Introduction
Les logiciels de géométrie dynamique doivent ce qu’ils sont, au moins en partie, au logiciel historique Cabri-géomètre développé à Grenoble par l’équipe de Jean Marie Laborde. On doit aux développeurs de ce logiciel d’avoir poussé très loin les mises en œuvre des principaux concepts liés à la manipulation directe (Shneiderman - 1983) et l’engagement direct (Nanard - 1990) en géométrie dynamique, au point que certaines de ces implémentations sont encore inégalées. Cabri est, de fait, une référence historique pour ce qui est de la mise en œuvre d’interface dans ce domaine.
L’héritage de Cabri-géomètre
L’équipe de développeurs et celle des didacticiens impliqués dans le projet Cabri-géomètre ont installé les premières réflexions sur la spécificité de concepts informatiques alors naissants, appliqués à la géométrie dynamique. Jusqu’où l’engagement direct peut-il aller ? Quels choix pour la dualité déterminisme/continuité ? Comment aller plus loin dans le traitement de l’a-modalité ? Comment faire évoluer le concept de micro-monde ...
Ce sont tous ces thèmes que nous allons revisiter dans les onglets suivants en illustrant les avancées en terme d’interface de la GD en général.
Voici un très bref résumé des spécificités de quelques uns des logiciels utilisés en France (ici ceux utilisés en formation initiale à l’IUFM de La Réunion ces dernières années)

La réification
D’une manière générale, par réification, on entend la transformation - ou la transposition - d’une abstraction en un objet concret. Par exemple, pour l’apprentissage du calcul au cycle 2, l’utilisation de collections organisées – doigts, constellations – pour un « calcul sur les objets » (Brissiaud - Ouzoulias), est une réification de la cardinalité dont l’efficacité a fait, entre autres points de la méthode bien entendu, le succès de la méthode PicBille.
En informatique, la réification consiste à transformer en objet informatique un concept (typiquement les palettes d’outils de tous les logiciels contemporains sont des réifications).
Mais pour parler véritablement de réification, des règles d’interaction instrumentale - au minimum la manipulation directe et l’absence de boite à dialogue - doivent être respectées :
« De nombreuses applications bénéficieraient de l’usage de la réification. Ainsi, les styles de Word n’ont pas réellement un statut d’objet : ils ne sont éditables que dans des boîtes de dialogue modales, et ne peuvent pas apparaître de façon permanente (à part dans le menu des styles) ; on peut cependant les stocker dans des fichiers. Dans Photoshop, les filtres sont des instruments, accessibles uniquement par l’intermédiaire de commandes et de boîtes de dialogue modales. Pourtant, les filtres sont centraux dans cette application de retouche photographique. En réifiant les filtres, il serait possible de créer des configurations prêtes à l’emploi, sans avoir besoin de spécifier les paramètres à chaque utilisation. »
Michel Beaudouin-Lafon (1997) - PDF
On voit que, dès 1997, la modalité est perçue comme un obstacle à la réification. C’est sur un constat de réification dégradée - et largement améliorable - que CaRMetal a vu le jour.
Un mot sur la genèse de CaRMetal ...
... car c’est une belle histoire du logiciel libre. Il provient de CaR (Compas and Ruler) un logiciel allemand (René Grothmann) avec un moteur mathématique particulièrement pertinent, pour plusieurs raisons dont l’extraordinaire anticipation des outils, les aspects conditionnels algébriques, la subtilité des macros ... Sa prise en main étant peu pratique - beaucoup d’aspect modaux, icones peu significatives - Eric Hakenholz a commencé par en améliorer l’interface (d’où le nom faisant référence au projet initial de modification de l’interface, c’était à l’époque de l’interface « métal brossé » des applications Mac ;-). Puis peu a peu, au bout de deux ans, la maintenance de l’interface au sein d’un logiciel en évolution devenant de plus en plus lourde, il a fini par développer un logiciel à part, et s’est ensuite autorisé à apporter des améliorations au sein du moteur interne du logiciel, jusqu’à en réécrire une grande partie pour la version 3.5 de CarMetal.
C’est désormais un projet déposé sur sourceforge avec tout ce que cela implique d’ouverture.
Dans ce texte on mentionnera le logiciel CaR pour dire que les fonctionnalités sont du logiciel initial de René Grothmann. On parlera de CaRMetal quand c’est un ajout ultérieur. CaRMetal est écrit en java, donc multiplateforme. Il est disponible pour Windows, Linux et Mac OS X.
Note : les définitions propres aux travaux de Shneiderman et de Nanard n’ont pas été reprises ici car on les trouvera dans ce compte rendu d’atelier de Eric Hakenholz réalisé au même colloque.
Anticip.
L’anticipation des constructions
Tous les logiciels de GD anticipent les items de création (segments, droites, cercles, polygones, coniques). Mais généralement, ils n’ont pas fait le choix d’aller plus loin, de proposer le même fonctionnement pour les outils de création (sauf Tracenpoche, en s’inspirant - d’après l’auteur - de CaRMetal).
Dans une société où l’apprentissage est permanent car les outils mis à notre disposition sont toujours en évolution, la logique contemporaine des logiciels est de contenir au sein même de leurs outils, une aide à leur propre apprentissage. L’aide peut être de bas niveau - on pense à la bulle rétroactive sur une icone qui rappelle sa fonctionnalité - ou intégrée à l’interface en accompagnant l’apprentissage dans la manipulation même de l’outil (Photoshop, Illustrator pour les logiciels professionnels, mais encore la suite iLife pour les logiciels grand public).
Instrumentation et instrumentalisation de l’anticipation
C’est le choix qu’à fait René Grothmann pour CaR et qui donc est intégré à CaRMetal. Ce choix pourrait paraître assez anodin tant l’utilisation d’un logiciel de GD pour sembler aller de soi, mais ce n’est pas le cas : l’anticipation des constructions provoque une toute autre instrumentation de la géométrie dynamique car, pour chaque outil, elle accompagne l’utilisateur - en particulier jeune - dans la construction de ses représentations du concept engagé.
Ainsi dans CaRMetal, si on veut tracer une parallèle à une droite donnée, la parallèle est portée par la souris, en translation, dès qu’une droite est sélectionnée, jusqu’à ce que l’utilisateur propose un point.
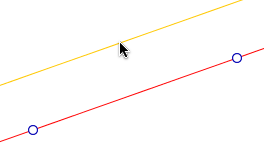
L’accompagnement que produit l’anticipation est cognitif : l’utilisateur (élève ou parfois étudiant dans l’exploration de micro mondes non euclidiens) voit le comportement géométrique de l’outil qu’il manipule, il l’interprète et construit ses représentations du concept qui sont naturellement bien plus conformes et rapidement stables que sans cet accompagnement.
Si l’engagement direct des logiciels de première génération reconnaît l’utilisateur comme sujet cognitif, une anticipation des constructions va plus loin, elle le reconnaît en plus comme sujet apprenant et accompagne son apprentissage.
Cette première analyse correspond à celle de l’instrumentation de cette anticipation des constructions. À un autre niveau, par exemple au lycée ou dans l’enseignement supérieur, l’anticipation peut aussi être instrumentalisée, au moins par l’enseignant dans un premier temps - sous forme de TP - avant de l’être par les élèves ou les étudiants. Cela peut conduire par exemple à une approche différente de l’investigation puisqu’il n’est plus nécessaire de finaliser une construction pour tester une conjecture. Au delà du gain de temps - réel - dans les phases d’exploration, c’est alors surtout une démarche cognitive réflexive sur la rétroaction observée du logiciel.
Un exemple élémentaire de cet enjeu est déjà présent dans la simple construction des médiatrices d’un triangle pour faire son cercle circonscrit : avec ce logiciel on rencontre naturellement - très régulièrement - une situation comme la suivante qui invite à la réflexion et à l’investigation : on s’apprête à construire la troisième médiatrice d’un triangle quand on passe à la souris sur une situation comme celle-ci :
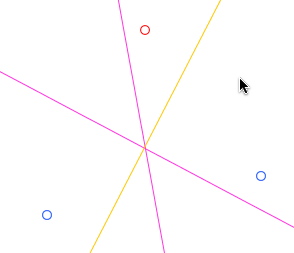
Alors qu’on voulait aller d’un sommet du triangle à un autre pour finaliser la figure, on passe par un point qui, en l’ajustant un peu, rend aussi les médiatrices concourantes, puis un autre à côté et plusieurs autres ainsi avant d’arriver au point que l’on devait cliquer. On a déjà construit l’image mentale d’un arc de cercle, soit par jeu, soit par curiosité intellectuelle, avant même d’avoir terminé la dernière médiatrice. Le cercle ensuite construit, cette observation fortuite peut être réinterrogée par l’enseignant pour une consolidation, par l’échange verbal, des schèmes qui se sont construits à ce moment.
On comprend bien toute l’instrumentalisation que l’on peut faire de cet outil, et la dimension auto-réflexive qu’elle permet pour peu qu’elle soit initiée et régulièrement réactivée en classe (même sans logiciel, dans l’environnement statique du tableau noir, comme démarche d’anticipation)
Anticipation dans tous les outils
L’anticipation de la construction est le fonctionnement naturel de tous les outils. La règle d’utilisation générique qui en découle est simple : si on hésite sur l’ordre des objets à montrer, on privilégiera toujours celui qui se termine par un point pour engager cette anticipation. Cela s’applique aussi aux macro-constructions :
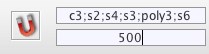
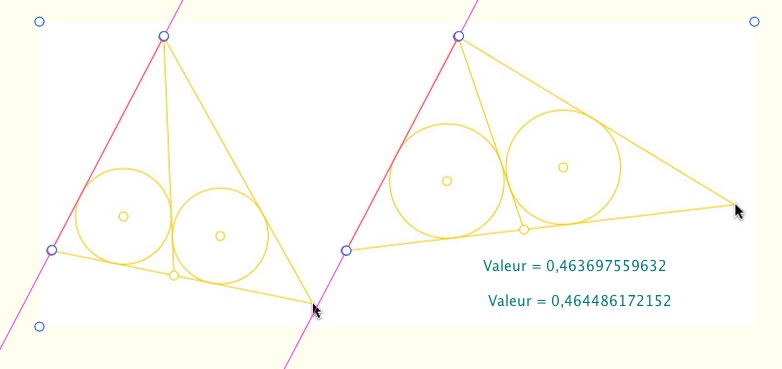
Voici deux instances, à partir des deux mêmes premiers points, d’une macro construction au moment où elle attend un dernier point. La macro construit le triangle, et partage celui-ci, à partir du premier sommet, en deux triangles ayant des cercles inscrits de même rayon.
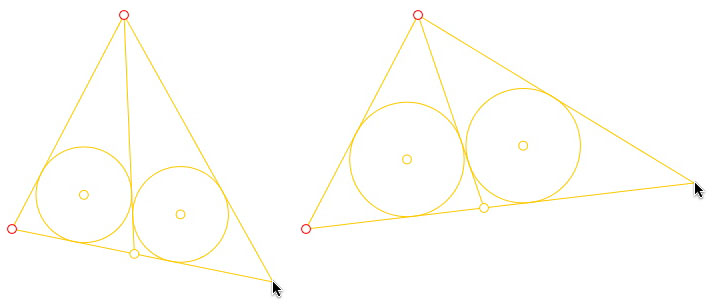
Quand le perceptif ne suit pas : par construction les deux segments opposés au pointeur dans les deux cas sont les mêmes - égaux et parallèles - ce qui ne se voit pas directement et demanderait ...
Et même au nommage automatique des points :
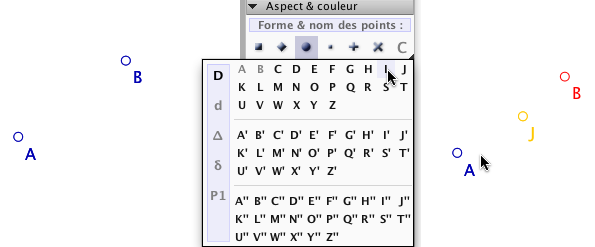
Sur la partie gauche, deux points et dans la palette d’outils on sélectionne le nom I comme nom du futur point construit. Dans la partie droite l’effet de la construction quand on veut prendre le milieu I de B et A : B a été sélectionné, alors le logiciel anticipe que le prochain point cliqué se nommera I et donc appelle naturellement J le milieu pré-construit. Bien entendu dès qu’on clique sur B, c’est le nom I qui est donné au milieu.
Pourquoi les autres logiciels sont-ils passés à côté de cette fonctionnalité ?
Avec le recul de l’expérience et de l’histoire de la GD, il peut être intéressant d’essayer une première analyse de cela. Nous allons le faire sur le référent historique qu’est Cabri-géomètre car ce sont les travaux et réflexions didactiques sur ce logiciel qui ont ouvert les portes à l’ergonomie que l’on connaît des logiciels de GD. Le fait que les autres aient pris les mêmes choix que Cabri tendrait à donner raison à Colette Laborde quand elle disait (colloque de l’IREM de Lille - 2008) que sur les 70 logiciels de géométrie dynamique qu’on peut répertorier, 60 sont pour l’essentiel des clones de Cabri.
Les plus anciens se souviennent des toutes premières versions du logiciel. Pour tracer une parallèle il fallait montrer dans un ordre précis, par exemple, la droite et le point. L’item attendait l’un puis l’autre, et comme il n’y avait pas – dans les premières versions – cet engagement direct qui, maintenant par exemple surligne l’objet qui peut être saisi, et que les items avait donc de fait un fonctionnement fortement modal, plusieurs personnes ont remarqué que cela serait plus simple, pour les élèves de collège en particulier si, quand les objets sont de types différents, on pouvait montrer les objets dans un ordre quelconque. Malgré la difficulté de la tâche, ce fut implémenté, et salué par chacun de nous comme un progrès de l’engagement direct sur les items de construction. En effet, l’intention de l’élève de construire une parallèle à une droite passant par un point était désormais encore plus reconnue si, l’outil sélectionné, il pouvait montrer d’abord le point. Cabri géomètre étant l’étalon de référence en géométrie dynamique, les logiciels suivant se sont généralement contentés de reproduire ce fonctionnement.
Dans CaRMetal il n’y a pas l’indépendance des objets de construction d’un item, mais il y a cette règle simple que tout est construit autour de l’anticipation, donc on sait que le dernier objet, quand cela a du sens, est un point. Par ailleurs, ce manque d’indépendance est largement compensé par la réaction immédiate du surlignage de l’objet quand il peut être sélectionné (comme avec Geogebra).
Il ressort de cette analyse que c’est le manque de début d’engagement direct (le surlignage), mêlé à la forte modalité interne des items de construction des premières versions qui ont fait prendre aux réflexions didactiques – puis aux mise en œuvre d’interface – des chemins qui, s’ils furent significatifs à l’époque de la mise en œuvre de la GD, n’était en définitive pas si optimaux que cela.
Modal.
La question de la modalité
Une tâche est dite modale si elle provoque une interruption de la situation en cours pour être effectuée. C’est typiquement une boite à dialogue par laquelle un élève modifie une couleur ou un aspect d’objets de la figure sur laquelle il travaille, ladite boite cachant généralement la figure (c’est régulièrement plus de 25% du temps devant une figure avec logiciel de GD « modal » en classe de sixième). CaR, comme d’autres logiciels de GD avait de nombreuses situations modales qui ont été rapidement enlevées dès les premières versions de CaRMetal. Ainsi l’utilisateur a toujours devant lui sa figure quoiqu’il fasse.
Mais cette question de la modalité va plus loin que ce premier aspect. Si on étend cette notion d’interruption à l’indisponibilité temporaire de la manipulation directe, alors les comportements des outils de construction qui ne créent les objets qu’après le dernier clic ont, en dernière analyse, des comportements modaux. Il ne s’agit pas ici de critiquer d’autres approches mais de voir qu’une fois les aspects les plus grossiers (boite modale en sur-couche de la figure) résolus, la réflexion sur la modalité peut se poursuivre et aller soit vers plus de confort d’utilisation soit vers un plus grand accompagnement du sens.
Par exemple l’a-modalité des aspects des objets était déjà présente dans les premières versions de CabriII (palette Attributs). Absente de CaR, elle a été rétablie dans CaRMetal et largement enrichie : outre les aspects usuels standards, tous ceux spécifiques à chaque objet comme le remplissage des cercles en disque, des polygones, l’affichage des mesures des longueurs peuvent tous être modifiés pendant la création de l’objet et avant le dernier clic pour cet objet.
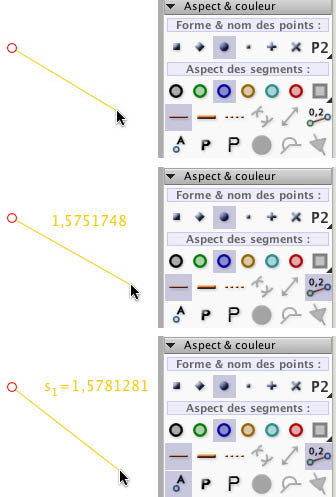
la mesure de sa longueur, puis son nom

le remplissage puis on change la couleur et l’aspect de ce remplissage
Repérer de la modalité cachée
En poursuivant la réflexion, on peut étendre la modalité à des représentations ou des modes d’organisation internes au logiciel, dont on peut dire qu’elle sont potentiellement porteuses de modalité.
De ce point de vue, on peut compléter l’analyse de la non anticipation des outils dans CabriII. La distinction, proposée dans les manuels d’utilisation de CabriII, reprises dans nos propres formations, entre les outils dits de création (série de 3 icones) de ceux dits de construction (autre série de 3 icones), bien entendu, d’un certain point de vue, fondée et signifiante, participe aussi d’une représentation porteuse de modalité. Une perception cognitivement différente des deux outils création/construction induit un traitement de l’engagement direct différent des deux situations au point qu’on ne voit perçoit même pas la modalité sous jacente.

Les raisons d’une perception cognitive différente de la création et de la construction peuvent être nombreuses et croisées. Il peut y avoir la dimension procédurale des constructions et l’unicité du résultat : étant donnée une droite et un point, il n’y a qu’une paralléle/perpendiculaire à la droite passant par le point, il suffit donc de la créer, il n’y a pas d’engagement direct sous-jacent comme dans une phase de création où tout est possible.
On voit bien qu’il y a là, de la part du concepteur, un effort à faire pour déceler un type de modalité dans cette vision de la construction d’un objet.
Une autre raison est peut être liée à l’organisation générale du logiciel dans son traitement de l’engagement direct. Pour renforcer la perception de l’utilisateur dans sa dimension cognitive, le choix a été d’avoir un retour textuel de l’engagement direct pour les constructions.
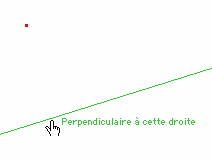
Et beaucoup d’énergie a été mise dans cette gestion - et surtout son traitement multilingue complexe. Il a pu en résulter une centration sur les prémisses de chaque outil (dont repérage du genre de l’objet dans la langue en cours, etc) pour affiner ce qui a fait ensuite la spécificité du logiciel et son label qualité. Au point que, à part René Grothman - qui, paradoxalement, avait par ailleurs un logiciel souvent fortement modal - personne n’avait vraiment perçu la possibilité bien plus centrée sur l’apprentissage par l’accompagnement des schèmes d’action de son implémentation des outils ...
... des outils, tout simplement, car dans cette démarche, il n’y a pas de distinction entre création et construction. Une parallèle est d’abord une droite crée qui a de plus une propriété, celle d’être parallèle à une autre. D’où dans CaRMetal cette palette de construction où par ligne, les objets sont - si possible - du même type : points, puis droites, segments et cercles.

Mais pourquoi cette quête d’a-modalité ? Pour en faire quoi ? Est-ce uniquement pour des considérations ergonomiques ? Voyons que non, que sous cette recherche de l’a-modalité, de nouvelles démarches ou de nouveaux outils peuvent se dégager.
L’extension de l’a-modalité : une source de nouvelles démarches d’investigation ...
Un exemple significatif est celui de l’animation, qui a longtemps été bloquante dans tous les logiciels, désormais a-modale dans la version 3.5. Cela signifie que l’on peut continuer la figure pendant des animations.
Loin d’être un gadget de programmeur - puisque c’est aussi un challenge - l’a-modalité de l’animation ouvre de nouveaux champs d’investigation : pour rechercher des invariants, on peut animer des objets et, pendant l’animation, conjecturer puis, infirmer ou confirmer ces conjectures par des constructions qui peuvent être testées - toujours en cours d’animation - par les outils de test appropriés.

Dans la situation précédente, le point bleu tourne autour du cercle extérieur. La construction est un exercice classique sur la recherche d’invariant (l’autre centre d’homothétie des deux cercles que le point de contact). Traditionnellement on conjecture le point invariant par l’animation du point bleu, puis on cherche une construction, et on confirme la conjecture en animant à nouveau le point avant d’entreprendre une démonstration. Ici on peut désormais faire les constructions pendant l’animation. Sur cet exemple la visualisation de l’invariant reste élémentaire car la droite des centres est fixe, mais dans d’autres situations, la visualisation de l’invariant ne peut s’obtenir qu’à travers l’animation.
... et de nouveaux outils
Un autre chapitre important dans la réécriture de CaRMetal a été l’a-modalisation des exercices pendant leur réalisation par les élèves. Cela suppose des procédures de validation très différentes des précédentes. La mise en place de ces procédures a rendu accessible la création de l’outil Monkey qui, dans le cadre de l’auto-validation, permet aux élèves d’un clic de secouer leur figure pour valider la construction.
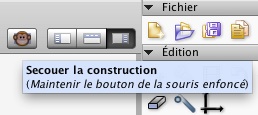
Le travail d’uniformisation des objets internes fait que les nouveaux exercices de CaRMetal peuvent s’appliquer à des scripts de programmation. Il en résulte que le module d’exercice est aussi (pour les élèves) un vérificateur de programme ou un outil de scripticiels pour les enseignants. Des articles de Alain Busser (entre autre) sur le sujet devraient bientôt être disponibles.
Comme on le voit la poursuite de la réflexion sur l’a-modalité est une source de progrès régulier de l’engagement direct en géométrie dynamique.
Logique
La géométrie logique
L’insertion d’éléments de logique dans les figures est d’une part un besoin qui s’est fait sentir très tôt et d’autre part un domaine sur lequel les interfaces et les outils disponibles, ont beaucoup progressé.
Un peu de préhistoire
L’expression géométrie logique remonte à 1993 quand, lors de la première Université d’été de géométrie dynamique (en fait « de Cabri Géomètre » dans sa première version) avec Charles Payan, de l’université Joseph Fourrier, nous avions tous les deux développé indépendamment des techniques géométriques pour introduire des comportements logiques dans les figures. L’importance (au moins opérationnelle) de ce concept a même été à l’origine de la revue papier abraCAdaBRI qui s’est ensuite transformée en site dont on peut encore lire les pages Alice. L’ombre du tiroir d’une commode avait été présentée en 1993, avec un logiciel qui n’acceptait alors que 500 objets maximum dans une figure.
Même si cela n’a pas été repris dans le site en ligne, nous avions développé à cette époque, dans la revue papier abraCAdaBRI, la notion ce CLFC : combinaisons linaires de fonctions caractéristiques ... entièrement en constructions géométrique, alors que la même chose se fait maintenant par un traitement algébrique des booléens. Les CLFC avaient été ensuite reprises et « popularisées » par Roger Cuppens dans ses ouvrages « Jouer ... avec Cabri-géomètre » (Brochures APMEP).
Les amateurs d’histoires anciennes peuvent s’amuser à feuiller les pages d’Alice de l’ancienne revue papier (les pages de la rubrique Espace ou celles du Hacker sont intéressantes aussi) conservées ici. On y voit de la passion pour la géométrie dynamique - et donc pour Cabri à l’époque - mais aussi le chemin parcouru depuis par les logiciels.
L’onglet Conditionnel de l’inspecteur d’objets
La géométrie logique de cette époque, entièrement géométrique, ne pouvait contenir que des « if … then » très limitatifs. Implémenté dans CaR, mais rendu bien plus accessible avec CaRMetal par un onglet spécifique de l’inspecteur d’objets – dans lequel on traite des objets déjà construits – la géométrie dynamique prend une autre dimension car tous les aspects d’un objet peuvent être conditionnés par des expressions algébriques liées à la figure.
Si vous avez téléchargé le logiciel, vous pouvez vous amuser, à partir d’un segment [AB] (clic droit sur le segment pour ouvrir l’inspecteur d’objets), à le mettre en bleu si x(A)>0, en rouge si x(A)<-1, et de plus en pointillé si y(A)>0 etc.
Rien qu’avec cet onglet, on peut traiter des situations réellement complexes comme on le verra dans le second onglet sur l’aimantation à propos de géométrie finie avec aimantation algébrique.
Voici un exemple tout à fait élémentaire, et assez prototypique de ce type de traitement pour enrichir les simulations que l’on peut proposer en classe. Deux segments [AB] et [CD] reposent sur le sol et sont posés contre un mur (ici ils sont élastiques car on peut déplacer les extrémités). On demande de mettre, dynamiquement, en gras rouge celui qui est au dessus de l’autre. Il s’agit d’une transcription dynamique d’un exercice classique papier crayon sur l’incidence et la projection orthogonale (exercice puisé dans un ancien Istra 1°S - IREM de Strasbourg).
Sur l’illustration de droite, on voit que - quand les projections orthogonales sur le sol (« ombres du sol à midi » en classe, si nécessaire) se coupent dans la partie où il y a une solution (du même côté que les pieds), ce point a alors deux antécédents I et J sur les bâtons - pardon les segments. C’est la clé de la solution.
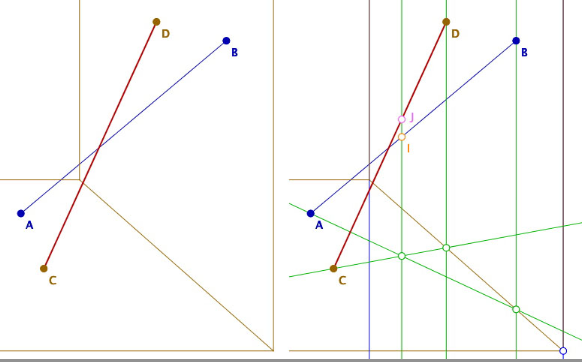
En classe de 1°S, il y a déjà quelques années, j’avais dû apporter de la ficelle et utiliser des élèves pour les extrémités des segments et d’autres élèves pour tenir les ombres au sol pour mettre en scène cet exercice. Il est intéressant de remarquer que ce n’était alors pas tant pour « confirmer expérimentalement » (pas assez de précision dans la manipulation finale de la droite (IJ)), mais simplement mettre en situation la plausibilité du raisonnement, car les élèves avaient alors eu besoin de raisonner non pas sur des figures, mais sur des objets.
Pour finaliser la figure avec l’onglet « conditionnel » de CaRMetal, il suffit alors de conditionner l’aspect gras et l’aspect rouge du segment sélectionné en fonction de l’ordonnée des points I et J :

Il faut bien entendu faire ceci sur les deux segments, en inversant le sens de l’inégalité, car le conditionnement est propre à chaque objet.
Les plus curieux pourront jeter un œil sur cette page pour voir comment on faisait (du côté de l’enseignant) quand tout devait être traité géométriquement. Cet exercice a longtemps servi en formation des enseignants comme introduction aux possibilités de la géométrie logique pour affiner les simulations en classe, c’est-à-dire aussi améliorer la perception du micromonde utilisé.
Les booléens de CaRMetal
Les expressions algébriques de CaRMetal peuvent être des booléens. Ou plus exactement les expressions qui valent 0 ou 1 sont considérées en interne comme des booléens. L’intérêt est de les utiliser à l’intérieur des coordonnées des objets et plus particulièrement des points. Par exemple pour un point U qui peux prendre 4 positions différentes I, J, K, O, position régie par des booléens associés EnI, EnJ, EnK, EnO, on peut donner pour U les coordonnées :

On construit alors un unique point U qui correspond à 4 cas de figure. Il s’agit ici de construire le cercle (de centre U donc) de plus petit rayon contenant un triangle ABC donné. Le cercle construit est unique et rend compte des 4 cas qui sont déclinés dans une preuve écrite :

La construction et son utilisation en classe sont détaillés dans cet article. Un exemple comme celui-ci permet, sur un problème simple, à la fois de travailler la logique au lycée, de la mettre en œuvre concrètement dans un logiciel et de voir comment on peut réifier l’unicité d’une solution mathématique dans un logiciel de géométrie dynamique contemporain.
Pour ceux qui ont lu les papiers préhistoriques, on voit que les CLFC sont bien un traitement en pur silex géométrique de ces mêmes questions, avec des contraintes particulières comme on peut le voir sur cet exemple de mise en oeuvre (PDF 70 Ko).
Désormais incorporés à la géométrie dynamique, accessibles aux coordonnées de points, les booléens nous permettent d’aller encore plus loin (si on le souhaite) en incorporant des combinaisons linéaires automatiquement itérées avec les CarScripts . On peut alors placer sur chaque point des dizaines de valeurs différentes sans effort particulier. C’est ce qui a été fait - comme exercice d’école - dans le premier onglet de cet article où l’on voit comment placer sur 8 points, les 92 positions de chacune des reines d’un échiquier dans le problème des 8 reines, un curseur balayant les 92 solutions. Les autres onglets de cet article en donnent une utilisation en statistique qui procure à un exercice classique une dimension « manipulation directe » surprenante.
Note technique sur l’usage des booléens : tous les langages de programmation ont une évaluation paresseuse des booléens, c’est-à-dire que si dans (a && b), a est faux, b n’est pas évalué, ou si dans (a || b) a est vrai, b n’est pas évalué. C’est parfois très intéressant si dans notre construction - dans des situation particulières(*) - certaines parties n’existent pas : le traitement paresseux bien utilisé peux alors éviter des constructions plus complexes.
Dans le même ordre d’idée, dans CaRMetal si a et b sont des booléens, a * b donne le même résultat que a &&b, à l’évaluation paresseuse près, justement : dans a*b, a et b sont toujours évalués. Les opérateurs & et | existent aussi en java. Ce sont les && et || mais sans l’évaluation paresseuse. Il ne semble pas qu’ils soient implémentés dans CaRMetal, mais de toute façon, pour ce qui nous intéresse, c’est équivalent au * et + de ci-dessus.
(*) Par exemple la prise en compte de l’éventuelle seconde intersection d’un cercle avec un segment qui, par construction a toujours au moins une connue.
3D
L’environnement 3D de CaRMetal
CaRMetal n’est assurément pas un logiciel 3D, et pourtant c’est bien plus qu’un logiciel 2D car un gros travail a été fait sur ses outils internes pour proposer un environnement 3D largement significatif non seulement pour un travail scolaire, mais pour bien plus comme nous allons le voir.
Quand on choisit de faire une figure 3D, un repère s’affiche ainsi qu’une nouvelle barre dans la palette d’outils. Ci dessous, saisie de l’environnement en cours d’utilisation :
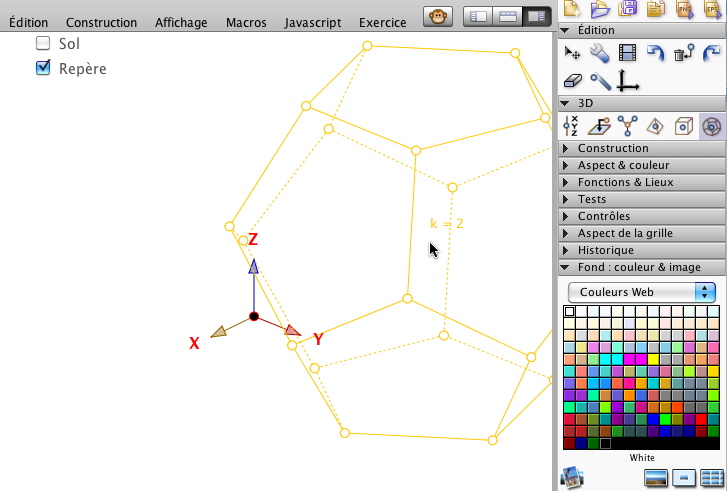
On observe la palette 3D ainsi que l’anticipation de la construction, y compris des arêtes cachées. Par contre sur cette copie d’écran, on ne voit pas l’information présente par défaut dans tout fenêtre 3D, à savoir qu’un clic-droit glisser permet de déplacer le trièdre en manipulation directe, dans une projection axonométrique.
Les outils disponibles
Le logiciel propose ces premiers outils de base

Quand on débute en 3D avec CaRMetal, il arrive souvent que l’on prenne l’outil Arête 3D pour ce qu’il n’est pas, il ne fonctionne que pour les arêtes, et pas sur les segments de ces faces. Dans la figure suivante (disponible en téléchargement dans un classeur de cet article) on distingue en pointillé les parcours sur les faces non visibles du cube, un traitement est fait (par script) à partir des arêtes cachées.
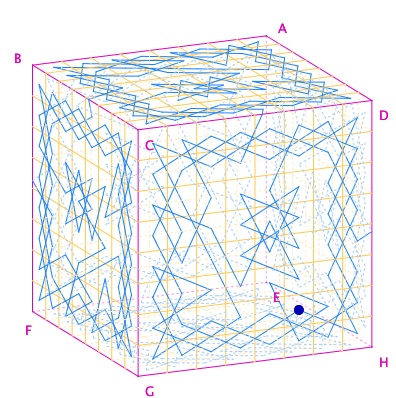
Puis les trois premiers polyèdres réguliers, avec gestion intégrée des arêtes cachées :

Pour utiliser l’outil « Point sur face », il faut d’abord construire le polygone associé à la face. Il peut être plein ou non. On pose tout simplement un point avec cet outil, le point est alors sur la face et conserve sa position barycentrique sur la face dans la rotation, comme on le voit sur ce dodécagone dans deux positions du trièdre de référence.
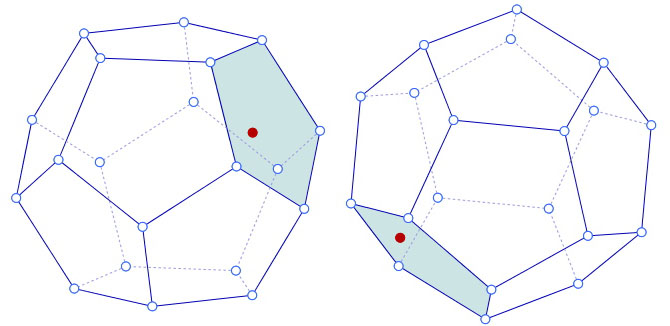
Quelques ressources 3D
Travailler en 3D est toujours long quelque soit le logiciel. Aussi les enseignants trouveront-ils en ligne les productions réalisées par les premiers utilisateurs.
Pour apprendre à utiliser les outils (sur l’exemple de la construction d’un tétraèdre ayant trois points sur le sol) on peut consulter ce tutoriel en flash, de Monique Gironce.
Pour une utilisation en classe, on peut télécharger les six exercices qu’elle a mis en ligne dans ce diaporama. On notera que les exercices sont prévus pour être faits en ligne. D’autres outils 3D sont présents, sous forme de macro, dans la dernière figure de cet autre diaporama. Voir aussi cette superbe troncature du cube.
Plusieurs figures sont disponibles en ligne sur les patrons. Tout d’abord les patrons dynamiques de pyramides (pour un usage en 4°), puis toujours sur les pyramides, ces figures de faux patrons. Egalement disponible, les développement de volumes qui ne sont pas nécessairement des polyèdre, dans ce magnifique diaporama de Monique Gironce.
Faire des patrons à ouverture dynamique est assez long, on se reportera à ce tutoriel pour le tétraèdre en flash et à celui-ci pour le cube (toujours de Monique Gironce). Tous ces tutoriels sont aussi téléchargeables sur le site de CaRMetal.
La gestion conjointe 2D et 3D
L’auteur de CaRMetal a développé des outils, d’utilisation élémentaire, pour permettre d’avoir dans la même figure une représentation 2D et une autre 3D liées entre elles. En pratique, dans une figure 3D, il suffit de créer un point « lié à la fenêtre » pour que ce point soit indépendant de la rotation du trièdre. Alors toute construction faite à partir de lui est aussi indépendante du trièdre.

Avec ces outils, on peut finaliser de superbes constructions comme celle-ci, où non seulement la boite est manipulable à la souris (trièdre) mais l’ouverture des côtés aussi par un curseur caché mais actif et accessible, juste sous la boite.
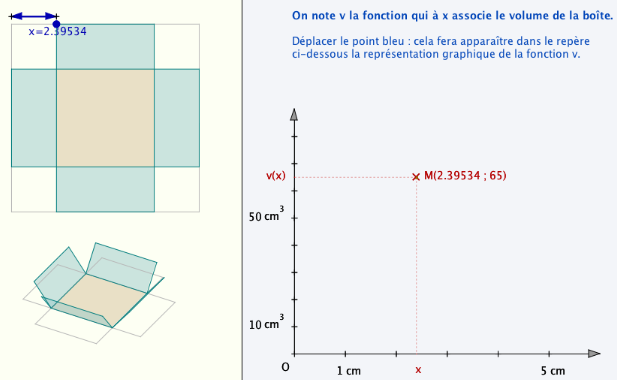
Quelques figures de ce type sont disponible dans ce diaporama (classe de seconde).
Un autre travail sur les fonctions de deux variables (ex-spécialité - BTS) est disponible dans la revue en ligne MathemaTICE, au paragraphe 3d de cet article dont le titre est « l’investigation en mathématique : une opportunité pour l’inventivité ».
Utilisation en géométrie différentielle
Nous quittons un moment l’enseignement au lycée pour voir que la partie 3D de CaRMetal a des utilisations tout à fait significatives dans l’enseignement supérieur, par exemple pour illustrer le concept de géodésique ou de géométrie non euclidienne dans un environnement où c’est la géométrie intrinsèque de la surface. C’est le cas de la pseudosphère. Beltrami a montré en 1868 que la géométrie de la surface (au sens de Gauss) est la géométrie hyperbolique de Lobatchevsky. En voici une illustration dans CaRMetal :
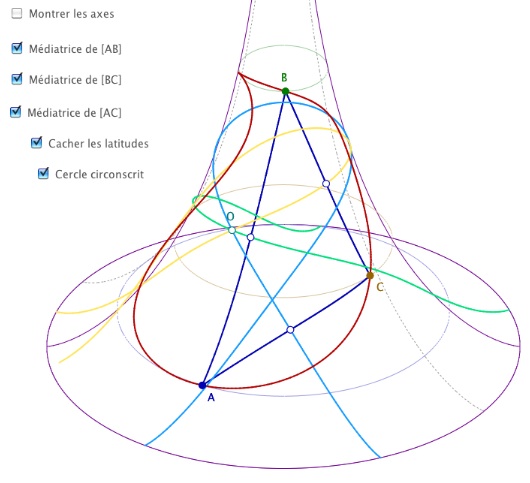
sur la pseudosphère (ici ce cercle existe)
Sans entrer dans les détails techniques de ces constructions, précisons tout de même un point qui montre le travail nécessaire en interne. Les sommets du triangle sont définis par une altitude (ici cachée pour l’esthétique de la figure) qui donne la position d’un cercle parallèle à l’équateur de la pseudosphère, et une longitude prise sur ces cercles. Dans la représentation 3D, les cercles sont des ellipses. Il faut que, quand la pseudosphère tourne, par exemple selon (OZ), les points tournent en même temps pour être conforme au plongement de la surface dans l’espace. Même si la situation est très simple ici, il y a un traitement à ajouter aux points sur objet d’une conique en fonction des points constituants de la conique pour obtenir un comportement, en 2D, conforme à la manipulation 3D.
Plus de figures sur la pseudosphère de Beltrami et la géométrie associée. Un des classeurs en ligne à la fin de cet article contient aussi le diaporama précédent.
Dét/Cont
Déterminisme et continuité
En géométrie dynamique, on dit d’un logiciel qu’il est déterministe si la figure revient à sa position initiale quand ses objets constituants, après manipulation, sont replacés dans leur position de départ. Dans un cadre scolaire, il est clair que le déterminisme – avec d’autres propriétés comme un fonctionnement intrinsèquement affine dans la déformation des figures – est dans le noyau du cahier des charges d’un logiciel de GD. Une autre propriété est dans ce noyau, la continuité, pendant la manipulation directe, des intersections des objets.
Mais la continuité et le déterminisme dans le même cahier des charges, est-ce possible ? Ce problème est connu sous le nom de conjecture d’isotopie (Ringel 1956), infirmée par Mnev en 1985 (donc avant la création des logiciels de géométrie dynamique). En résumé (extrait de la thèse de Bernard Genevès - 2004 - Université Joseph Fourier d Grenoble - « Vers des spécifications formelles : fondements mathématiques et informatique pour la géométrie dynamique. ») :
« la continuité et le déterminisme des constructions sont incompatibles : il faut privilégier l’un ou l’autre, on ne peut maintenir les deux simultanément jusqu’à leurs conséquences. »
Un projet remarquable a été mené dans le cadre de la continuité, dans les années 1990-2000, le logiciel Cinderella, dans sa version 1 (logiciel ni libre ni gratuit). Les auteurs - Jûrgen Richter-Gebert et Ulli Kortenkamp - ont bien montré que la question de la continuité nécessitait un plongement dans un plan projectif complexe. Pour une utilisation scolaire, la version 2 de Cinderella est redevenue déterministe.
Maintenir la continuité
Une des tâches des pionniers de la géométrie dynamique a donc été de concilier les contraintes de déterminisme avec des choix de continuité. Non seulement on arrive, pour les figures usuelles (cercles / droites) à gérer correctement la continuité des intersections, mais Cabri a inventé deux types d’intersections, l’intersection d’objet et l’intersection « à la volée », où l’on désigne celle des deux intersection que l’on veut. Alors pour l’intersection d’une droite et d’un cercle, l’intersection à la volée (montrer à la souris le point que l’on veut prendre sur l’état de la figure à l’écran) résiste au passage à l’infini du rayon du cercle (« persistant namming problem »), alors que ce n’est pas le cas des points obtenus par intersection de deux objets, c’est-à-dire en montrant sccessivement les deux objets.
En terme de continuité, c’est une avancée importante qui a été reprise par les logiciels de nouvelle génération comme Geogebra et CaR. L’utilisateur retiendra que pour mieux préserver la continuité dans les figures, quand il y a plusieurs intersections, il est préférable de prendre l’intersection « à la volée ».
Et essayer d’aller plus loin
Mais ces deux logiciels ont fait un effort supplémentaire pour installer la continuité le plus loin possible. On sait d’avance qu’il n’y a pas de proposition totalement satisfaisante, mais cela n’empêche pas d’améliorer quelques outils. Dans Geogebra l’utilisateur peut « activer » une option de continuité générale à une figure. La continuité de l’intersection d’un cercle et d’une droite est satisfaite quand le cercle passe par un rayon infini, sans même qu’on ait fait l’intersection « à la volée ». CaRMetal, propose pour les points d’intersection, une personnalisation individuelle plus algorithmique.
Par exemple la saisie à la volée de l’intersection de deux cercles n’est continue dans aucun logiciel. On peut voir à ce sujet, l’onglet « Exercice » de cet article de présentation des nouveautés de CaRMetal 3.5. C’est le cas dans la construction très usitée du 4° point du parallélogramme au compas. La démarche algorithmique de CaRMetal est alors particulièrement efficace :

En cliquant sur l’intersection à la volée des deux cercles, on peut ensuite affiner l’algorithme interne de l’intersection en précisant le point comme étant « loin de » B. Alors la continuité est préservée ... ce qui est aussi un joli exercice à proposer.
On le voit, les choix des deux logiciels sont différents. Le problème difficile de l’intersection de deux arcs de cercles (intersection de deux droites hyperboliques) quand l’un des arcs change d’orientation (la droite hyperbolique passe par le centre du disque de Poincaré) est bien résolu par les deux. Il y a donc un vrai progrès dans la gestion interne des objets malgré une impossibilité générale théorique.
Le carcan du déterminisme
Pour certaines situations, le déterminisme est un carcan dont on aimerait pouvoir sortir.
L’exemple le plus simple est celui de l’enroulement de la droite sur le cercle. Les angles en géométrie dynamique sont traditionnellement mesurés entre 0 et 2π alors que l’on a souvent besoin d’enrouler sur plus d’un tour. Par exemple dans la construction suivante, les points A, B et C sont a priori sur la feuille principale de la pseudosphère (longitude dans [-π, π[). À gauche le point B s’apprête à franchir la frontière de la feuille (+π) mais le déterminisme fait que la figure se retrouve (à droite) dans la position où B serait, à quelques pixels près, juste avant la même ligne frontière (-π).

Nous verrons plus loin d’autres spécificités de CaRMetal qui permettent – de deux manières différentes – de s’affranchir du déterminisme de façon choisie, contrôlée et mathématiquement significative. En particulier nous verrons que l’on peut résoudre, dans le contexte dynamique de la manipulation directe, cette question, dite de l’uniformisation du cercle.
Paradigme
Nouveau paradigme pour enseigner la géométrie
Depuis plusieurs années déjà, chacun s’accorde pour reconnaître que la géométrie dynamique a créé un nouveau paradigme pour l’enseignement de la géométrie (Michèle Artigue 2007). Cet onglet voudrait illustrer que ces possibilités – soit de présentation soit d’exploration dynamique par les élèves, se transposent dans l’enseignement supérieur. Avec sa capacité à construire des micromondes, la géométrie dynamique est d’une grande efficacité pour l’exploration de géométries spécifiques, peu étudiées, ne se prêtant pas à l’investigation classique, ou encore pour aller plus loin dans l’exploration de modèles bien connus mais pour lesquels on n’avait pas encore d’accès dynamiques en manipulation directe. Nous allons dire quelques mots sur deux exemples.
Micromonde et macros implicites
Le concept de micromonde remonte aux travaux de Seymour Papert (qui le défini dans « Jaillissement de l’esprit ») avec sa « géométrie de la tortue » et le langage Logo. « Smaltalk » (premier langage orienté objet) est une autre tentative de micromonde. On sait - en accéléré - que c’est de là qu’est venu l’interface du premier Macintosh (première interface graphique présenté comme un micromonde).
Au sens de Papert, comme structure qui réifie les objets mathématiques et les opérations sur ces objets par la manipulation directe, et comme environnement d’apprentissage ouvert, les logiciels de géométrie dynamique sont tous, de fait, des micromondes. Toutefois, dans le cadre de la géométrie dynamique, de part son champ d’application spécifique, on s’entend généralement pour donner une définition plus restrictive au concept de micromonde.
On dira d’un logiciel de géométrie dynamique qu’il est un micromonde s’il permet de créer de nouveaux outils (macro-constructions) et de les structurer pour permettre un environnement propre à un contexte géométrique particulier.
La question de la structure est plus ou moins finalisée, selon les logiciels, ou de façons différentes. Les choix de Cabri, très centrés sur cette définition forte des micromondes, n’ont jamais été égalés semble-t-il depuis, avec ses possibilités de personnaliser ses macros par des icones et surtout ses barres de menu. Ci dessous une barre de macros sur la pseudosphère (version CabriII 2001 d’où la petitesse des icones, depuis elles ont quadruplées) et une autre sur le disque de Klein Beltrami (KB).pour travailler sur la pseudosphère par conjugaison.
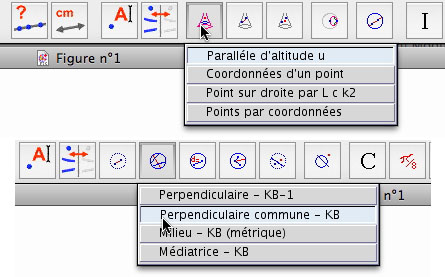
On perçoit bien le plongement dans le micromonde par les menus iconiques. Mais d’autres progrès sont possibles (et ont aussi été fait par Cabri depuis cette époque). Dans la mise en place de la barre de menu de 2001 sur la pseudoshère, il avait fallu rivaliser d’ingéniosité dans l’organisation de toutes les constructions pour faire que l’ensemble de l’environnement soit entièrement inclus dans la donnée de la conique équateur afin de n’avoir à fournir, comme unique donnée environnementale sur la surface pseudoshérique, que cette information supplémentaire. On arrivait alors à se limiter à 3 objets pour l’interfaca pseudosphère-KB.
CaRMetal n’a pas de barre de menu iconique ni de palette personnalisable (pas encore). Toutefois ses macros sont très organisées et hiérarchisées. Elles sont du coup toutes accessibles à la fois, non exclusives l’un de l’autre. Ci-dessus on voit à gauche les macros standards livrées avec le logiciel (les dossiers contiennent parfois de nombreux sous dossiers et à droite des dossiers de macros ajoutées, construites par l’utilisateur.

Ces macros ont surtout une propriété essentielle par rapport à ce qui pouvait se faire en 2001, celle d’avoir des objets implicites. Ainsi pour envoyer un point de KB vers la pseudosphère, il y a plus aucun objet préalables à fourni pour décrire l’environnement, on ne clique que sur le point que l’on veut envoyer. Le sentiment d’imprégnation dans le micromonde géométrique est autrement plus profond, on n’a plus à désigner les considérations techniques qui permettaient cette modélisation, nous sommes directement dans le modèle. Mais surtout, il n’ y a plus à concevoir une préparation des figures pour minimiser au maximum la description de l’environnement. Depuis Cabri a aussi intégré les macros implicites.
Ces précisions étant faite sur les micromondes, leur degré de réalisation, leurs évolutions, voici deux exemples abordés succintement dans des contextes non euclidiens. Le premier a pour objectif - sil devait être utilisé en formation (ce qui n’a pas encore été possible) de poser une réflexion à la fois sur les choix axiomatiques et sur les représentations que nous pouvons avoir nous même, par exemple de l’orthogonalité et de ses propriétés. Le second est une construction plus classique d’une figure sur la pseudosphère ayant des contraintes particulières.
La géométrie non arguésienne - l’exemple du plan de Moulton
Dans les premières éditions de son ouvrage Les Fondements de la géométrie, Hilbert a proposé un exemple de géométrie non arguésienne, à l’intérieur d’une ellipse, qui respectait tous ses axiomes sauf celui sur la relation entre la congruence des angles et des segments (en fait un cas d’isométrie des triangles). Il s’agissait d’illustrer que sans cet axiome on ne peut démontrer le théorème de Desargues dans le plan : Hilbert a montré que dans cette géométrie, le théorème de Desargues n’est pas vérifié.
Ensuite, en 1904, Moulton a proposé un modèle non arguésien beaucoup plus simple. Les points de sa géométrie sont ceux du plan réel. On se place dans un repère orthonormé du plan. Les points de sa géométrie sont les points du plan. La droite (AB) est, selon les positions de A et B :
– la droite euclidienne (AB) si celle-ci est parallèle à l’axe des ordonnées ou de pente positive ou nulle.
– les droites affines par morceaux quand la pente (euclidienne) est négative avec une brisure sur l’axe des ordonnées, la pente étant le double dans le demi plan (x >0) que celle dans le demi plan (x<0).
L’intérêt de construire un micro-monde – ie avec des objets de cette géométrie manipulables comme ceux du logiciel, en particulier en pouvant traiter leurs intersections - est d’aller très vite dans l’exploration des propriétés de cette géométrie.
Le plan de Moulton est non arguésien, et en particulier, même s’il existe des parallèles (avec l’axiome d’Euclide des parallèles vérifié) la géométrie n’est pas affine.
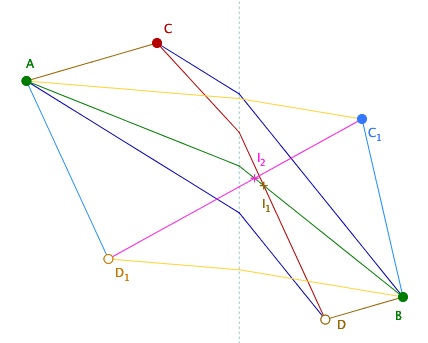
Ci-dessus, on part d’un segment [AB]. Depuis un point C on construit le parallélogramme ACBD et l’intersection $I_1$ des diagonales. On recommence avec un point $C_1$, le parallélogramme $AC_1BD_1$ et $I_2$ l’intersection des diagonales. Il n’y a pas coïncidence des points, les diagonales d’un parallélogramme ne se coupent pas en leurs milieux. Il n’y a pas de barycentre, ni de géométrie des coordonnées.
Le plan de Moulton étant localement euclidien, sauf aux points de l’axe des ordonnées, on peut aussi travailler sur l’orthogonalité. La perpendiculaire à une droite donnée en un point donné est plus délicate à construire car si généralement elle existe, il peut dans certains cas ne pas y en avoir et dans d’autres en avoir deux.
En fournissant les macros du micro-monde à des étudiants, et plus particulièrement à de futurs enseignants, il est facile de concevoir une exploration - plus ou moins guidée selon le projet - de cette géométrie loin des standards non euclidiens , où la somme des angles peut être parfois supérieure à 2π, et parfois inférieure. On peut proposoer de déterminer les extrema de la somme des angles d’un triangles, faire réaliser ces extrema.

On peut envisager de faire explorer cette géométrie sur les configurations usuelles et chercher des conditions suffisantes pour retrouver certaines propriétés classiques (ici la question de l’orthocentre).
Pour chaque droite, en vert la partie du plan d’où on ne peut mener aucune perpendiculaire à la droite, en rose celle dans laquelle par chaque point il a deux perpendiculaires.
À gauche : cas où il y a orthocentre (hauteur à pente négative issue d’un somme à deux côtés de pente négative … à condition (à droite) que les intersections des hauteurs soient bien dans le même demi plan par rapport à l’axe des ordonnées. Entre les deux figures B n’est déplacé que de quelques pixels pour faire basculer la hauteur issue de A, d’un côté de la zone verte pour (BC), à l’autre côté.
L’enjeu d’une telle pratique pour des futurs enseignants est la réactivation de la curiosité – et de la précision - sur les propriétés de géométrie élémentaire comme elle peut être enseignée en collège et la prise de distance vis à vis des réflexes mathématiques quand on n’a jamais rencontré de contre exemple. Par exemple dans cette géométrie, la distance d’un point à une droite n’est pas réalisée par le segment orthogonal (alors que c’est le cas en géométrie hyperbolique et en géométrie elliptique) :

Plus de détail sur le plan de Moulton dans ce diaporama.
Les maximas des angles d’un triangle sont étudiés ici.
Un autre exemple sur la pseudosphère de Beltrami
Nous avons déjà abordé la notion de micromonde construit autour de la pseudosphère. Donnons un autre exemple de construction dynamique que, peut-être, seul ce type d’environnement peut produire. On se propose cette fois de « donner vie » à une phrase un peu malheureuse de Coxeter, c’est-à-dire construire une situation réelle correspondant à son interprétation des droites de la pseudosphère. En effet, au détour d’une phrase, Coxeter laisse à penser qu’elles s’enroulent à l’infini sur la surface alors qu’on sait qu’elles sont bornées en altitude, qu’elles partent de l’équateur pour y revenir.
“Every geodesic that is not merely a meridian winds itself round the ‘horn’ as it proceeds in one direction whereas in the opposite direction it is abruptly cut off by the cuspidal edge.”
H.S.M. Coxeter, Introduction to geometry, 2nd ed., New York : Wiley, p. 378
On se propose donc de construire une courbe ayant un sens géométrique – si possible élémentaire – qui s’enroule à l’infini sur la surface depuis l’équateur. La pseudosphère est aussi appelée, selon une terminologie installée par Kein, surface pseudosphérique parabolique car la partie du plan hyperbolique qu’elle représente ne peut approcher qu’un seul point à l’infini du plan hyperbolique : d’un point de vue projectif, comme la parabole la pseudosphère n’a qu’un point de contact avec la droite à l’infini.
Ce point s’atteint soit selon tout méridien quand l’altitude augmente (ce qui peut avoir un rapport avec la représentation de Coxeter), soit encore en s’enroulant infiniment sur un cercle parallèle à l’équateur. En effet, les cercles parallèles à l’équateur de la pseudosphère (en terme euclidien, avec le plongement de la surface dans l’espace de dimension 3) sont des horicycles(*) pour la géométrie de la surface.
(*) Il y a trois types de faisceaux de droites hyperboliques : les faisceaux à centre (droites concourantes en ce point), les faisceaux à axes (droites ayant cet axe comme perpendiculaire commune) et les faisceaux « sans support » (ou « à point idéal"), c’est à dire les droites parallèles, se coupant en un point idéal du plan hyperbolique. Hilbert, comme Bolyai, parlait de « bouts » pour le point idéal.
Alors si on appelle cycle l’image d’un point par toutes les symétries d’un même faisceau, il y a trois types de cycles : les cercles – dont le centre est le centre du faisceau – les équidistantes – dont l’axe est l’axe du faisceau, et les horicycles – pour lequel le point idéal du faisceau est parfois aussi appelé « centre ». Les équidistantes ne sont pas des droites en géométrie hyperbolique. Ce dernier point a souvent été à l’origine de preuves fausses du V° postulat d’Euclide où implicitement on utilisait qu’une « équidistante » est nécessairment une droite.
Tous les méridiens de la pseudosphère sont des droites en faisceau « sans support » (ie des droites parallèles au sens de la note ci-dessus) de centre l’unique point idéal de la pseudosphère. Il en résulte que si on construit un triangle ayant trois points sur une équidistante dont un méridien donné est l’axe, cette équidistante aura le point idéal de la pseudosphère comme point limite à l’infini et donc s’enroulera à l’infini sur la surface.
Voyons maintenant comment construire cela concrètement. Nous allons cette fois utiliser la conjugaison avec le disque de Klein Beltrami (KB).
Dans KB, l’image de la pseudosphère (PS) est l’intérieur stricte de l’ellipse de centre $O_{dl}$ et de petit axe [$O_{Ex}$$I_{dl}$]. Le point $I_{dl}$ est le seul point à l’infini accessible à la pseudosphère. Sur PS on se donne deux points A et B (manipulables en longitude, et en altitude par $u_A$ et $u_B$). Ils sont envoyés sur KB. On construit la médiatrice (bleue) de leurs images, puis le méridien rouge orthogonal à cette médiatrice passant par $I_{dl}$.
D’un point P de ce méridien est issue une perpendiculaire (orange). C’ est le symétrique de A’ par rapport à cette droite. Le triangle A’B’C’ ayant deux médiatrices qui ont – par construction - une perpendiculaire commune (le méridien rouge), les trois médiatrices du triangle – dont on sait qu’elles sont toujours en faisceau – sont nécessairement en faisceau à axe.
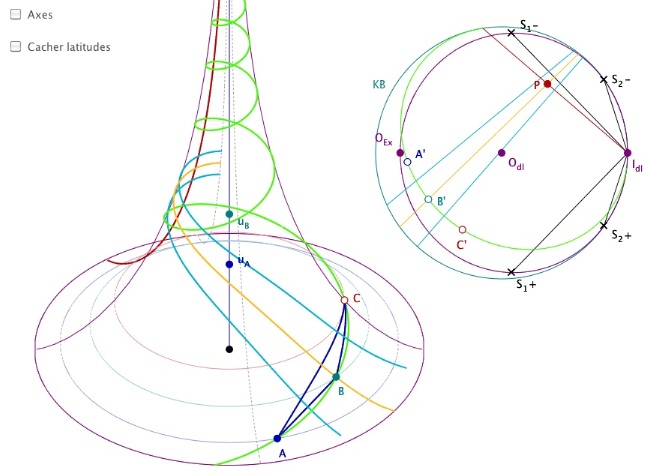
Il en résulte que A’, B’, C’ sont trois points d’une équidistante d’axe un méridien, et dont un des deux points limites est l’unique point idéal $I_{dl}$ accessible à la pseudosphère.
Renvoyons cette construction sur la surface (dans l’illustration précédente, les médiatrices ne sont tracées que sur la feuille principale pour plus de lisibilité). Le point C est donc un point construit à partir de A et B pour que le triangle ABC soit sur une équidistante d’axe le méridien rouge (de la PS) et s’enroulant sur la surface à l’infini. Dans cette construction, cette figure est directement manipulable par les points $u_A$, $u_B$, A et B.
Ces deux exemples veulent seulement illustrer que, moyennant un travail préalable de construction des outils des micromondes que l’on veut explorer [ce qui est un trés beau challenge pour l’enseignant], la géométrie dynamique est aussi un nouveau paradigme pour l’enseignement de la géométrie, même dans l’enseignement supérieur.
Aimant1
Aimantation et réalité mathématique augmentée
Les points libres – et uniquement ceux-ci – peuvent être aimantés par d’autres objets (points, segments, droites, cercles, polygones, etc.) avec un rayon d’aimantation commun ou propre à chaque objet. On clique simplement sur les objets qui vont attirer le point sélectionné. Puis on donne un rayon.
Avec un rayon important, en pratique tout se passe comme si le point était sur la figure constituée de la réunion des objets attirants. Ci-dessous, l’image par une symétrie orthogonale d’un point M aimanté.
Dans cette utilisation, l’aimantation est une extension topologique de la notion de point sur objet en point sur figure.

Premières utilisations didactiques : du continu au discret
Déjà dans ce simple contexte, pourtant élémentaire, une utilisation de l’aimantation permet de mettre en place des ingénieries nouvelles pour la géométrie des configurations. Afin de dégager plus clairement l’importance de cette utilisation, revenons un instant sur un des sens que l’on donne à la géométrie dynamique.
On a régulièrement dit, depuis longtemps, au début dans un discours critique avant d’en reconnaître l’intérêt, que la géométrie dynamique est une géométrie qui valide une propriété par résistance au mouvement – ie à la manipulation directe. La propriété (concours des médianes, des hauteurs d’un triangle) est alors découverte – et conjecturée - en manipulant une figure, en tant qu’invariant, un peu comme des lois physiques. La géométrie dynamique place l’élève dans un contexte scientifique comme observateur et expérimentateur sur le monde géométrique qu’il a à étudier. La critique portait non seulement sur l’utilisation du mouvement en mathématique mais surtout sur la pertinence de l’observation dans un monde que l’on veut a priori présenter et enseigner comme hypothético-déductif (*).
Or, bien sûr il n’y a pas de mouvement dans une figure, même quand l’élève déplace un sommet du triangle à l’écran. Il n’y a que des instances des points constituants - et donc des instances de la figure. Il n’y a que des réalisations successives de dessins d’une seule figure géométrique. Il n’y a pas de mouvement car il n’y a pas de temps dans les figures. Comme construction d’objets ayant des relations mathématiques entre eux, elles sont a-temporelles. Le temps est du côté de l’utilisateur quand il déclare qu’il « déplace les sommets depuis 20 s et les droites se coupent tout le temps (**) » c’est-à-dire dans toutes les instances observées : c’est l’utilisateur humain qui est plongé dans le temps pas la figure géométrique. Et c’est cette rencontre entre la temporalité de l’utilisateur et l’a-temporalité de la figure mathématique dans un contexte d’instanciation facilité qui fait de la géométrie dynamique un nouveau paradigme pour aborder la géométrie.
Cette description du paradigme de la géométrie dynamique - comme relation entre le mouvement des objets à l’écran par la manipulation de l’utilisateur et l’a-temporalité des figures – renforce de fait une représentation de la géométrie dynamique déjà implicitement plongée dans un contexte continu : l’invocation du « mouvement » des figures, du temps de l’utilisateur s’ajoute à la problématique de la déformation barycentrique, du suivi continu des intersections. Même si personne n’oublie que le nombre de pixels à l’écran est fini, le paradigme de la géométrie dynamique est habillé de continuité.
Notes
(*) Ce point est simplement réfutable en précisant que les mathématiciens, de tout temps, ont toujours expérimenté même sur les nombres ou les structures. La critique s’est alors portée sur la question des premières représentations que l’on donne de la démarche hypothético-déductive puis peu è peu s’est éteinte devant la richesse du concept de géométrie dynamique et ses propres arguments de renforcement de la nécessité de la démarche finale de preuve.
(**) L’élève rajoute même parfois « au même point » pour rendre compte de la concourance des droites alors que le point de concours se déplace à l’écran avec son mouvement de la souris. Ce raccourci linguistique, dénote (ou participe à la construction au moment où il est prononcé) un début de conceptualisation qu’il y a là un invariant et donc une propriété particulière.
Manipulation directe discrète sur configuration finie
Nous allons voir qu’une approche particulière, mais importante, de l’aimantation va être d’étendre cet habillage implicite au discret. Par l’aimantation, les élèves vont pouvoir expérimenter – puis raisonner - sur des configurations finies, a priori fixes, avec la même richesse de manipulation que le permet la géométrie dynamique. C’est pour cela que nous disons que l’aimantation étend la pertinence de la géométrie dynamique aux configurations finies. Voyons cela sur un exemple (figure disponible dans le classeur Aimantation).
On s’intéresse à la propriété du quadrilatère orthocentrique : dès que H est orthocentre de ABC, alors tout point A, B C (ou H) est orthocentre du triangle formé par les trois autres points. Ce théorème est généralement travaillé non pas pour son résultat, mais pour mettre en œuvre le changement de point de vue sur un même dessin vis à vis des côtés et des hauteurs.

Dans la figure précédente, un point H est aimanté par les trois sommets d’un triangle et son orthocentre, il ne peut prendre d’autres positions. Ensuite un jeu sur les noms des points permet de rendre le visuel ci-dessus . Dans cette manipulation, on a choisi de faire que H soit toujours l’orthocentre de ABC, chaque point semblant se déplacer en manipulant « à la main » (en manipulation directe) le point H sur l’un des 4 points. On rend ainsi visible la propriété qu’on veut montrer, par exemple que (HC) est toujours perpendiculaire à (AB) et donc que chaque point est orthocentre des trois autres. On transforme ainsi une configuration finie statique en une configuration finie dynamique avec une manipulation directe discrète limitée à ce que l’on veut étudier.
Un autre exemple, identique mais dans un contexte plus complexe, aura cette fois, explicitement, pour but de montrer l’intérêt d’apprendre (ou de connaître) une configuration plutôt qu’un théorème :

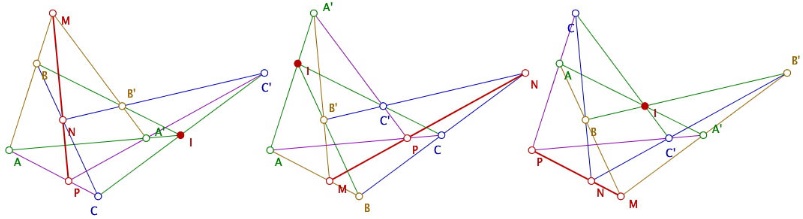
Cette configuration est symétrique, elle comporte 10 points et 10 droites, chaque droite contient 3 points et par chaque point passe 3 droites. Il en résulte que chaque point de la configuration peut être le point I de l’hypothèse initiale et chaque droite, la droite des points alignés M, N, P. Pour montrer qu’il est préférable de connaître la configuration plus que l’énoncé formel du théorème, on peut proposer une figure, où, comme la précédente, I est aimanté par les points de la configuration et quand on déplace I, tous les points se déplacent sur la configuration ainsi que la droite des points alignés M, N, P :
Dans les deux cas l’effet, en situation, est saisissant en terme cognitif, comme si un saut avait été franchi dans le regard des configurations finies. C’est la raison pour laquelle nous y percevons une extension du paradigme de la géométrie dynamique aux configurations finies, par aimantation.
L’utilisation de l’aimantation dans un contexte fini peut avoir une utilisation plus technique. Par exemple pour rapidement émettre des conjectures sur les sous groupes des groupes des racines $n^{ième}$ de l’unité, on peut travailler dans ce contexte :
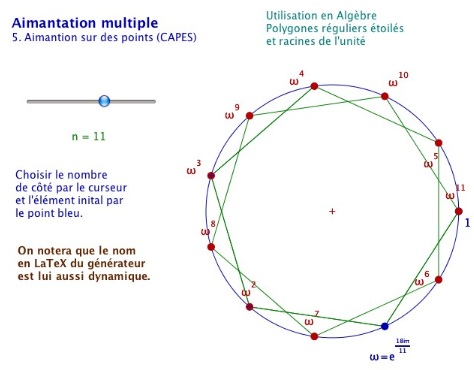
Là encore le point ω est aimanté sur les racines de l’unité, en fonction de la valeur n du curseur. La présence du curseur et le nom des points donnent une certaine technicité à la figure qui n’a pas l’épure à la fois esthétique et conceptuelle des deux précédentes.
Il est intéressant d’observer que, même si elle traite elle aussi de configurations finies, le rapport au discret ne s’installe pas de la même façon. Les étudiants restent plus « plongés dans le plan complexe » que sur une configuration finie. Une raison possible est que cette figure – contrairement aux deux configurations précédentes - est là pour apporter plus qu’elle-même, elle est constamment interprétée en terme de structure algébrique, de générateurs de sous groupes.

Mélanger le continu et le discret
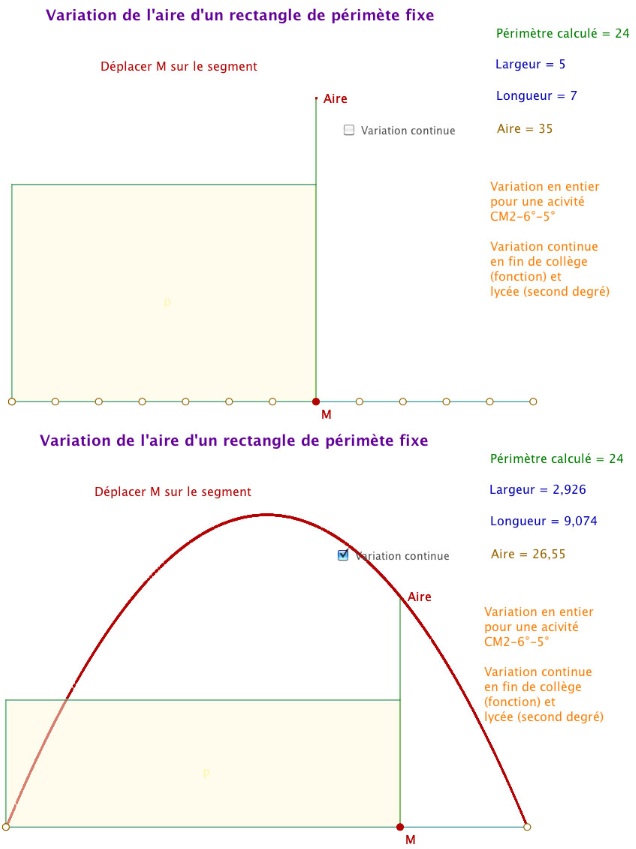
Un même problème peut avoir des approches à différents niveaux de la scolarité, dans un contexte continu ou dans un contexte discret. On s’intéresse ici à un problème qui est soulevé en classe de CM2 quand on travaille sur la non relation variationnelle entre l’aire et le périmètre. Typiquement il s’agit de mettre en défaut la représentation - très installée - que plus le périmètre est grand (plus on a de ficelle pour entourer) plus l’aire (entourée) est grande. On travaille par exemple avec des rectangle de périmètre constant, on demande d’en construire - sur du papier quadrillé - avec des mesures entières pour constater que les aires sont différentes et même, éventuellement se questionner sur l’aire maximale observée.
Voici donc une figure (disponible dans le classeur aimantation) qui permet de travailler avec des entiers - éventuellement en CM2 on peut enlever le segment avec l’aire et ne s’intéresser qu’aux valeurs numériques et à l’illustration - mais aussi de manière continue pour d’autres classes. La figure n’a été faite qu’à des fins de formation pour illustrer la continuité des thèmes dans l’enseignement en formation continue, elle n’a pas été utilisée en classe.
Aimantation et réalité mathématique augmentée
Dans le contexte d’une illustration ou d’une simulation, la manipulation directe présente le défaut – didactiquement important – de généralement ne pas pouvoir passer par certains points significatifs de la figure puisque ceux-ci ne rentrent pas dans le réseau des pixels exactement accessibles à la souris.
Ainsi si un segment est simplement partagé en 3, par le théorème de Thalès, sauf configuration très particulière, il n’y a aucune chance qu’un point sur objet d’un segment manipulé à la souris puisse passer par un point au tiers d’un segment.
L’aimantation va permettre d’enrichir la manipulation directe et augmenter la pertinence mathématique des figures d’où cette expression de réalité mathématique augmentée.
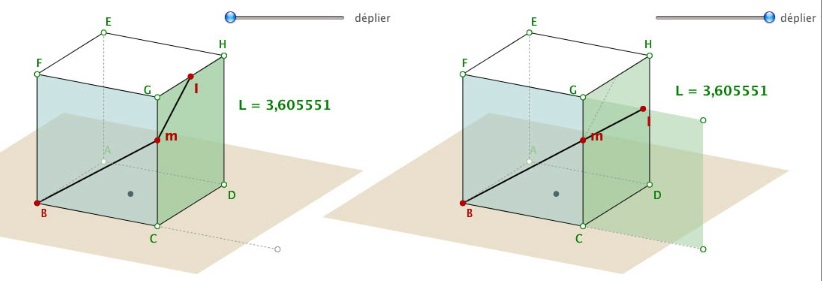
Dans l’exemple suivant, on veut aller de B à I en passant par l’arête [CG] par un trajet minimum. Il est facile de voir que le trajet est minimum quand le point m est au tiers du segment [CG], point inaccessible en manipulation directe.

Comme les points sur objet ne peuvent être aimantés, on aimante m à la fois fortement sur l’arête, et à un pixel sur le point solution. Dans ce cas le point m paraît passer naturellement sur le point solution puisque physiquement il y passe à moins de 1 pixel, l’aimantation ne se voit pas, on conserve l’impression de continuité tout en enrichissant la manipulation directe.

Dans le cas de cette figure de démonstration (réalisée par Monique Gironce de l’IREM de Toulouse), on a choisi une illustration un peu ostentatoire (un curseur apparaît quand on passe sur le point solution) pour montrer en même temps qu’avec la gestion conditionnelle, on peut faire apparaître un curseur jusque là caché, qui conduit à une autre possibilité d’action, elle-même conduisant à la perception claire de la solution :
Nous utiliserons ultérieurement cette notion de réalité mathématique augmentée dans un contexte plus riche.
Erreur d’exécution plugins/auto/sarkaspip/v4.1.0/noisettes/document/inc_images_jointes.html






Commentaires