Le déroulage d’un patron de cube est un sujet à la mode, alors autant commencer par lui.

Le tétraèdre régulier a aussi droit à son patron, bien plus simple que celui du cube puisqu’une fois déplié, c’est un triangle équilatéral :

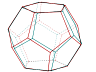
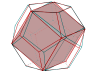
Voici un exemple de dodécaèdre régulier (pas de patron cette fois-ci) orientable à volonté avec la souris (on peut aussi zoomer avec la molette de la souris)

Si on colle sur chaque face d’un octaèdre régulier, un tétraèdre régulier de même arête (donc 8 tétraèdres en tout, on obtient la figure ci-dessous qui est d’ailleurs la réunion de deux tétraèdres réguliers, dont l’intersection est l’octaèdre de départ ; son nom est stella octangula :

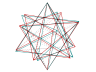
Une autre étoile semi-régulière, celle ci à 12 branches :

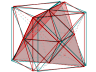
Le fameux tétraèdre régulier inscrit dans un cube :

Dans le même cube on peut inscrire un deuxième tétraèdre régulier ; si on colorie les faces des deux tétraèdres on ne voit plus grand-chose puisque la réunion des deux tétraèdres est la stella octangula vue ci-dessus. Alors le deuxième tétraèdre est resté transparent :

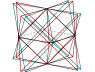
De même, on peut inscrire 5 cubes dans un dodécaèdre. Le dessin avec les 5 cubes se trouve ici : On comprend qu’on hésite un peu à en faire un anaglyphe ! Alors un seul cube est représenté ici :

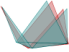
Encore une figure à manipuler : Un cube qui, une fois ouvert, s’est transformé en 3 pyramides : Ceci explique le dénominateur 3 dans la formule $volume=\fracbase \times hauteur3. Ceci nécessite tout de même que soient admis d’une part que le volume d’une pyramide ne dépend pas de la position du sommet mais uniquement de la hauteur, et d’autre part que ceci se généralise aux autres formes de pyramides :

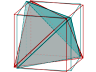
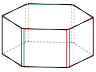
Enfin la figure suivante représente au choix une pyramide ou un prisme, il suffit de choisir son plat (pas si plat que ça si on a des lunettes anachromes !) sur le menu (déroulant) :

Les figures de l’article sur les polyèdres remarquables peuvent aussi concerner le collège.