Groupes de rotations en anaglyphes

vendredi 1er mai 2009
par  Alain BUSSER

La géométrie dynamique permet de visualiser une rotation d’axe $\alpha$ en appliquant à une figure donnée toutes les rotations d’axe $x \in [0 ;\alpha]$ où $x$ est pilotable par curseur. Dans l’espace, cette possibilité est particulièrement intéressante : Essayer de reproduire les figures ci-dessous avec des patrons relève de la gageure...

Groupe du tétraèdre

Seule une rotation pas trop évidente du tétraèdre est montrée ici, les autres se concevant plus facilement par l’imagination :

rotation tétraèdre

Groupe du cube

Tout d’abord, les rotations autour d’un axe de coordonnées :

cube axe perpendiculaire

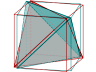
Ensuite, les rotations plus difficiles à concevoir, autour d’un axe passant par les milieux de deux arêtes opposées :

cube axe médian

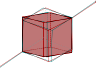
Enfin les rotations du tétraèdre inscrit dans le cube, qui expliquent par exemple la présence d’un hexagone régulier dans le cube :

cube axe diagonal

La récapitulation utilise plus les fonctions avancées de l’outil texte de CarMetal que les anaglyphes mais bon...

groupe du cube

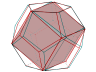
Groupe du dodécaèdre

Représenter les 60 rotations serait un peu difficile alors on se contentera d’un dénombrement :

groupe du dodécaèdre

Commentaires

Logo de Dominique TOURNÈS
jeudi 7 mai 2009 à 17h42 - par  Dominique TOURNÈS

Avec mes étudiants préparant le CAPES, nous faisons traditionnellement l’inventaire des sous-groupes finis de O+(R3). Cette année, j’ai utilisé les anaglyphes d’Alain pour leur faire établir la liste des rotations du tétraèdre, du cube et du dodécaèdre. Les étudiants, munis de leur lunettes anachromes, ont apprécié ! Malheureusement, on n’a pas bien vu le relief : cela marchait très bien sur l’écran de l’ordinateur portable, mais beaucoup moins sur l’image projetée au vidéoprojecteur. Sans doute faudrait-il disposer d’un réglage variable selon la distance où l’on se trouve par rapport à l’écran ? Cela ne nous pas empêché de profiter pleinement des figures et de la possibilité de faire tourner les polyèdres : en les mettant dans des positions adéquates, on voit très bien les rotations associées aux faces opposées, aux arêtes opposées, aux sommets opposés, et en faire la liste est facile. Merci donc pour cet outil qui m’a permis d’aller beaucoup plus loin que dans mes cours des années précédentes.