Documents à télécharger

– Documents Word : fiche guide et déroulement
– Fichier Excel : explorations
– Fichiers GéospacW : xOy.g3w , yOz.g3w , xOz.g3w et chgtrep.g3w (copier le texte de la figure dans Editer >> texte de la figure puis Executer)
– Fichier DERIVE : paraboloide
– Fichiers Dpgraph : figure 1 et figure 2 (vous devez avoir préalablement téléchargé le logiciel gratuit DpgraphViewer)

Étude de la figure S d’équation $z^2=x^2+y^2$

Lors de la séance précédente, les élèves ont établi l’équation cartésienne d’un cylindre illimité d’axe (Oz) à partir de considérations géométriques. Nous avons ainsi illustré le passage du géométrique à l’analytique.

Dans cette séance, il s’agit du passage inverse. La figure S est donnée par une équation cartésienne qui n’est pas connue des élèves. Nous allons montrer que l’étude des sections de S par des plans parallèles aux plans de coordonnées permet de mieux appréhender la figure dans l’espace.

Le tableau à compléter (fichier Excel) est une sorte d’entrée en matière, une exploration naïve de la situation ; l’élève se construit ses premières représentations.

On s’intéresse ensuite à la nature des sections de S par des plans parallèles aux plans de coordonnées. On commence naturellement par les plans parallèles à (xOy). On met facilement en évidence (fichier chgtrep.g3w) que M a pour coordonnées (x, y, a) dans (O, i, j, k) si et seulement si M a pour coordonnées (x, y) dans (A, i, j) où A(0, 0, a).

Très rapidement, les élèves obtiennent une équation de la section de S par le plan $P_{a}$ d’équation z = a dans le repère (A, i, j) : $z^2=x^2+y^2$. S’ensuit une discussion suivant les valeurs de a.

Le logiciel GéospacW permet de représenter la courbe d’équation $x^2+y^2=a$ dans le plan variable $P_{a}$. Les flèches du clavier combinées aux commandes "sélection >> trace" permettent de faire varier a et de visualiser la figure S comme une surface engendrée par les sections (fichier xOy.g3w).

On pratique de manière analogue pour découvrir les sections de S par des plans parallèles à (xOz).

Aux noms des variables près, les élèves devraient reconnaître l’équation caractérisant la section de S par le plan $Q_{b}$ d’équation y = b : $z=x^2+b^2$ dans le repère (B, i, k) où B(0, b, 0) dans (O, i, j, k).

Le logiciel DERIVE permet de tracer quelques-unes de ces courbes dans un même plan par une simple formule :

Le logiciel GéospacW permet de dessiner [1] la courbe d’équation $z=x^2+b^2$ dans le plan variable $Q_{b}$. Les flèches du clavier combinées aux commandes "sélection >> trace" permettent de faire varier b et de visualiser la figure S comme une surface engendrée par les sections (paraboles) (fichier xOz.g3w).

On procède de même pour les sections de S par des plans parallèles à (yOz) (fichier yOz.g3w).

Enfin, les logiciels DERIVE et Dpgraph permettent de visualiser directement la figure en 3D à partir d’une équation

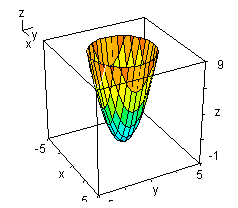
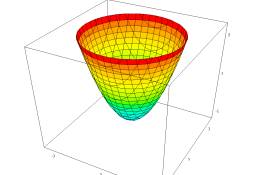
DPGRAPH présente l’avantage de gérer les équations implicites du type f(x, y, z) = 0. Les figures sont d’une qualité exceptionnelle et les sections par des plans d’équations z = k sont représentées.