Construction du cube

Sous CaRMetal, il est aisé de construire un cube : C’est une macro de l’espace ! Il suffit donc de cliquer sur « nouvelle figure 3D » (dans le menu « fichiers ») puis de sélectionner l’outil de création de cube. Ensuite le centre du cube suit la souris, et ci-dessous il a été placé (par un clic) sur l’origine du repère. Avec le cube, est fourni un nombre appelé k, initialement égal à 2, qui donne la taille du cube (valeur absolue des coordonnées des sommets). Il a été remplacé par 1,732 (et rendu invisible) pour que le cube rentre dans la fenêtre et les sommets ont été renommés. C’est l’étape la plus longue du TP !

Construction de I et J

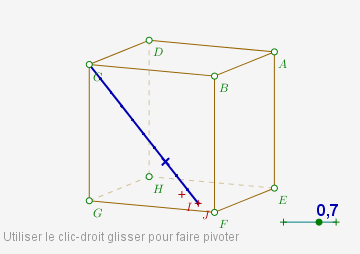
Le cube est représenté en perspective cavalière. Celle-ci conserve les milieux et les centres. I est donc le milieu de [EG] et J est le milieu de [IF]. C’est tout !

Coefficient m

m est un réel compris entre 0 et 1, donc idéalement matérialisable par un curseur. Cependant

• On doit pouvoir (ci-dessous) construire un lieu dépendant de m ;
• le curseur doit être « flottant », c’est-à-dire qu’il doit rester collé à la fenêtre, et pas tourner avec le cube lorsque celui-ci tourne avec le clic-droit-glisser.

Pour ces deux raisons, le curseur a été choisi dans les macros « expert ». Il s’appelle « curseur linéaire continu », et on peut l’agrandir, le déplacer etc. Bien entendu la valeur minimale est 0 et la valeur maximale est 1. Il a également fallu renommer m l’expression pilotée par le curseur.

Barycentre

La perspective cavalière conserve les barycentres. C’est le principe de ce corrigé.

CaRMetal possède plusieurs macros pour construire des barycentres de deux ou trois points pondérés, mais outre le fait que créer un point pondéré est un peu long (il faut entrer le coefficient !), il y a ici 4 points. On commence par constater que la somme des coefficients est 4 (c’est d’ailleurs la première chose à faire face à un barycentre : vérifier qu’il existe, ce qui se fait bien par un calcul de la somme des coefficients).

Alors on crée un point (en bleu ci-dessous) auquel on donne les coordonnées suivantes :

(m*x(E)+2*m*x(F)+m*x(G)+(4-4*m)*x(C))/4

(m*y(E)+2*m*y(F)+m*y(G)+(4-4*m)*y(C))/4

L’outil « lieu » (en cliquant sur le point bleu puis en double-cliquant sur le point vert du curseur) donne alors le lieu souhaité (en bleu ci-dessous). Ne pas hésiter à manipuler le curseur et à faire tourner la figure pour vérifier que le lieu est bien un segment.

En résumé, ce TP est très rapide (ce qui laisse du temps pour les démonstrations) si on le fait avec le bon outil, et avec un minimum de préparation (savoir ce qu’est un barycentre, mais aussi comment on calcule ses coordonnées).