Les graphes, pour quoi ?

L’histoire de la théorie des graphes débuterait avec le mathématicien suisse Leonhard Euler au 18^e siècle et trouve son origine dans l’étude de certains problèmes, tels que celui des ponts de Königsberg, la marche du cavalier sur l’échiquier, le problème du coloriage de cartes et du plus court trajet entre deux points.

C’est plus récemment, en 1822, que le mot « graphes » est introduit par le mathématicien et géomètre anglais James Joseph Sylvester.
L’avènement des graphes est alors une révolution conceptuelle qui fait voler en éclats plus de deux millénaires de géométrie : en théorie des graphes, la forme n’a pas d’importance, c’est-à-dire que tous les repères géométriques hérités de la géométrie euclidienne classique deviennent caducs, au profit d’une notion unique, celle de lien entre les points. Depuis le début du 20^e siècle, cette théorie constitue une branche à part entière des mathématiques.

Il y a actuellement plusieurs types d’applications, mais la principale se rencontre en informatique. Les graphes sont une structure mathématique particulièrement bien adaptée à l’ordinateur : ils servent de structure de données, c’est-à-dire qu’ils permettent d’organiser des ensembles d’objets (des noms, des nombres, des suites d’opérations…) de façon simple et pratique à exploiter.

Les graphes, pour qui ?

Pour toutes ces raisons, la question d’installer à moyen terme les graphes dans les curricula du collège ne semble pas complètement saugrenue. Tout comme les probabilités et les statistiques ont fait leur apparition il y a quelques années au lycée, puis au collège plus récemment, cette intégration montre l’intérêt en général du renouvellement des curricula en adéquation avec les outils des problématiques sociales actuelles.

La question que nous pouvons nous poser au départ est : pourquoi un chapitre sur les graphes apparaît-il seulement dans les programmes de la spécialité mathématiques de terminale ES ?
Serait-il pertinent d’insérer cette branche des mathématiques dans d’autres classes ?

J’ai donc testé si les graphes pourraient être traités dans des classes de collège, à condition bien évidemment que le contenu soit adapté !!!

Cet article est ainsi constitué de deux parties :

• une première partie théorique d’initiation à la théorie des graphes se rapportant au programme actuel de terminale ES spécialité mathématiques ;
• une seconde partie avec une perspective plus didactique et pédagogique sur l’expérimentation de quelques notions de graphes dans des classes de collège, en particulier en sixième, cinquième et quatrième.

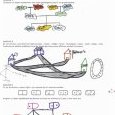
Premier document

La première partie porte sur la mise en place de quelques exemples de la vie courante et du vocabulaire de base, puis sur les différentes utilisations pratiques des graphes :

• recherche de l’existence d’une chaîne ou d’un cycle eulérien ;
• coloration d’un graphe ;
• recherche d’une plus courte chaîne d’un graphe pondéré ;
• caractérisation des mots reconnus par un graphe étiqueté ;
• recherche d’un état stable d’un graphe probabiliste ;
• caractérisation des graphes planaires.

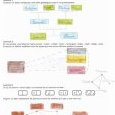
Second document

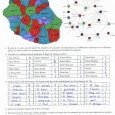
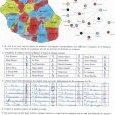
La seconde partie concerne le compte rendu de l’expérimentation faite en classe sur les thèmes des graphes planaires, des chemins et de la coloration des graphes.
Ce document est accompagné de l’ensemble des fiches données aux élèves lors de l’expérimentation.

Concernant ce premier test en collège, les différentes séances menées sur les graphes ont été accueillies plutôt favorablement par les élèves (le thème a été plutôt accrocheur car ludique et très différent de ce qu’ils ont l’habitude de faire).

Perspectives éventuelles

Le nombre de concepts étudiés est sans aucun doute un peu ambitieux, et le choix de conduire la même expérimentation pour les trois niveaux de sixième, cinquième et quatrième a servi à tester à quel niveau correspondait le mieux telle ou telle notion.
Il est clair que toutes les notions étudiées ici ne doivent pas figurer dans un seul niveau de classe, mais qu’il faut en effectuer une répartition intelligente.

S’il fallait introduire des notions de graphes au collège, cela pourrait par exemple se faire suivant le programme suivant :

• les premiers éléments des graphes, de par leurs aspects ludiques, installent une véritable dévolution des problèmes rencontrés en classe de 6^e ;
• les notions de chaine et de cycle sont l’occasion, dès la classe de 5^e, de traiter de raisonnements mathématiques et d’aborder la distinction entre un cas général et un cas particulier ;
• la notion de chaine eulérienne est une ouverture vers d’autres démonstrations arithmétiques en classe de 4^e ;
• la colorisation pourrait être réservée à la classe de 3^e, en prenant le temps d’en détailler un algorithme.

On peut cependant se demander si un tel saupoudrage ne conduirait pas à une trop grande dispersion, et s’il ne vaudrait pas mieux se limiter à deux niveaux, par exemple 4^e et 3^e ?

Évolution dans les programmes actuels

En Terminale ES, des changements sont d’ores et déjà en cours pour la rentrée 2012 : l’option mathématiques a disparu en première, et la spécialité a perdu 30 minutes. En revanche, tous les contenus inhérents aux graphes sont maintenus, au détriment des équations cartésiennes de l’espace, des suites et des fonctions à deux variables, preuve de l’engouement pour la notion.

De même, l’enseignement de l’ISN (Informatique et Sciences du Numérique) comme quatrième spécialité offerte en terminale S à la rentrée 2012 implique l’utilisation de graphes en lien avec l’informatique : structuration et organisation de l’information (des documents unis par des liens hypertextes fournissent un exemple de classement de type graphe), algorithmique avec la recherche d’un chemin dans un graphe par un parcours en profondeur (DFS), les réseaux et le routage (de type arborescent et de type graphe).