La représentation graphique de la fonction $(x,y) \mapsto xy$ est un paraboloïde hyperbolique dont wims fournit l’image suivante :

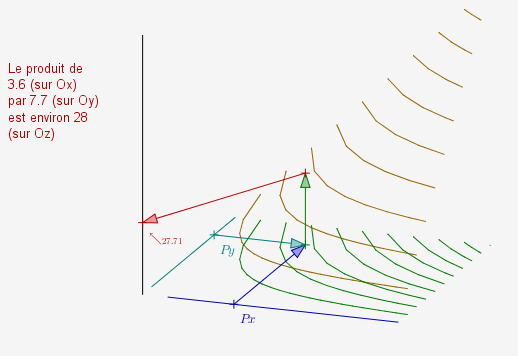
Ainsi, dans l’espace, pour calculer graphiquement le produit de deux nombres $x$ et $y$, il "suffit" de repérer $x$ sur l’axe des abscisses et $y$ sur l’axe des ordonnées, puis, à l’intersection des parallèles à ces axes menées par ces points, repérer le point de coordonnées $(x ;y ;0)$. Par celui-ci, la verticale (parallèle à l’axe des $z$) coupe le paraboloïde hyperbolique au point de coordonnées $(x ;y ;xy)$ dont il suffit alors de lire la hauteur (ou cote) sur l’axe des $z$. Le fichier est téléchargeable ci-dessous (fichier "PH dynamique"). Une fois ouvert sous CaRMetal (patience !) il se manipule de façon plutôt fluide compte tenu de sa taille. En voici une copie d’écran :
Pour la maniabilité des figures, on cherche une représentation plane, obtenue en projetant les hyperboles ci-dessus sur le plan $z=0$ :
Si on regarde le paraboloïde hyperbolique d’au-dessus, on obtient la figure plane suivante "abaque de Pouchet dynamique" téléchargeable ci-dessous, et elle aussi longue à ouvrir :
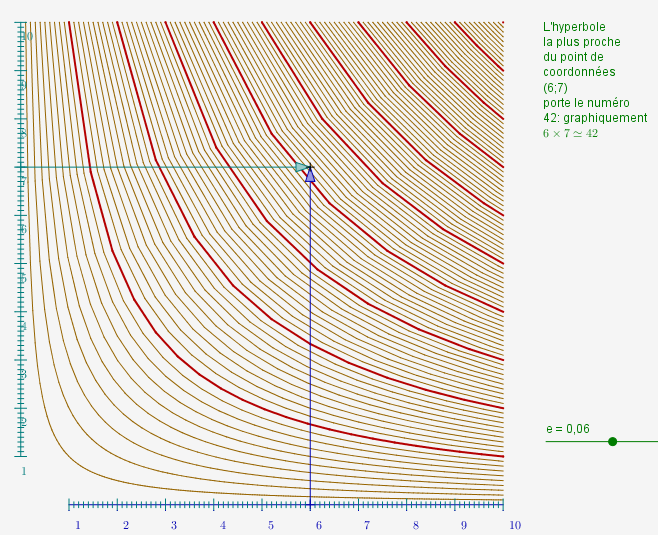
Voici l’abaque :
Cet abaque de Pouchet permet de calculer graphiquement un produit. Ci-dessous on peut télécharger la version pdf, prévue pour être agrandie en A3 par la photocopieuse (donc avec un coefficient de 141%), que l’on peut manipuler en classe avec deux équerres, l’une pour l’axe des abscisses, l’autre pour l’axe des ordonnées. Pouchet avait préféré rajouter sur son graphique, un grillage style "papier millimétré" pour éviter le recours à ces équerres, mais ceci alourdirait encore la figure, qui est déjà assez chargée avec 100 arcs d’hyperboles (dont 1, réduit à un point).
Le fichier pdf a été obtenu en écrivant un petit programme dans le langage Asymptote.
Les paramètres les plus intéressants à modifier sont les suivants :
- h est la largeur des graduations sur les axes de coordonnées (celle qui est réglable par curseur dans la version CaRMetal).
- unitsize conditionne la taille de l’image.
- Le 0.2 dans la définition de thin stipule que les traits sont tracés avec une épaisseur du cinquième de celle du trait normal.



Commentaires