(english)

Le support de cet article va être l’expérience de Buffon qui est le premier à avoir trouvé une relation statistique impliquant le nombre Pi. Il est composé de deux parties principales : la mise en place de la simulation (figure 1) puis la convergence du quotient étudié vers pi pour un grand nombre de lancers (figure 2).

On se souvient - en relisant cette page par exemple - que si d est la largeur des lames de parquet et a la longueur des aiguilles, la probabilité qu’une aiguille jetée au hasard coupe soit sur deux lames est $\frac{2a}{\pi d}$. Et la loi des grandes nombres permet de dire qu’avec un nombre important de lancers on arrive à approcher pi. Le même article (en 3.7) précise que l’on obtient une meilleure estimation de pi pour a = d, ce que nous allons prendre.

1. Préparation de la figure

Comme dans l’article d’introduction à la fonction random, nous allons utiliser un bouton Marche/arrêt (variable a), un point M qui se déplace sur un cercle de rayon fixe. Les lames de parquet seront des segments allant de -5 à 5 en abscisse comme en ordonnée (en pratique cela ne sert pas, c’est juste pour le rendu de la simulation).

Pour le lancer d’une aiguille nous allons utiliser trois variables : xA, yA et t. Un point A va être de coordonnées (xA,yA) et un point B de coordonnées (xA+cos(t), yA+sin(t)) ainsi [AB] est de longueur 1.

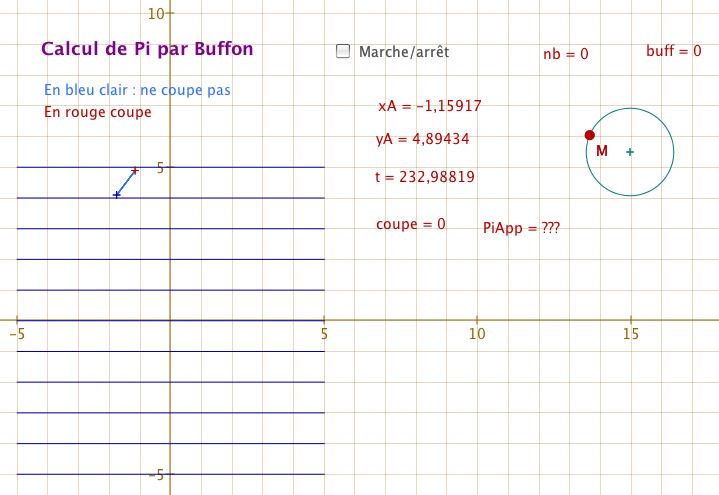
Quelques précisions
xA = -5+random(10)
yA=-5+random(10)
t=random(360)
Au passage l’angle nul n’a aucune chance de se produire, mais comme toute autre valeur particulière : ce n’est pas ni un défaut ni un problème.
Précaution importante
Comme déjà mentionné dans l’article précédent, si on donne les coordonnées aléatoires à A et à B avant de construire le segment on n’a aucune chance d’arriver à construire [AB] - mais essayer, c’est amusant. Il faut d’abord construire un segment [AB] puis modifier les coordonnées de A et B.
Modifications pour la figure en ligne
Dans la figure en ligne, pour éviter d’avoir trop d’aiguilles déjà dessinées avant de cliquer sur le bouton Marche/Arrêt, on a modifié les coordonnées de A et B de la façon suivante :
Pour le point A : if(a==0 ;0 ;xA) en abscisse et if(a==0 ;0,5 ;yA) en ordonnée,
et pour le point B : if(a==0 ;1 ;xA+cos(t)) et if(a==0 ;0,5 ;yA+sin(t))
Cela ajoute 4 tests pour le tracé d’une aiguille, on peut l’éviter pour une construction en local.

2. Mise en place de la simulation

Nous définissons maintenant trois nouvelles variables, nb, coupe , et buff. La première est récursive et définie ainsi :

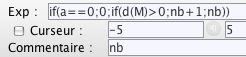
Par rapport à la même variable de l’article précédent, on notera que l’on a ajouté un second test conditionnel en dehors de l’initialisation. Ainsi seul un clic sur le bouton Marche/Arrêt réinitialise le nombre de lancers, un simple clic sur la figure va arrêter simplement l’animation - car d(M) va devenir nul - et les calculs en cours sans les réinitialiser.

La variable coupe indique quand une aiguille coupe une lame de parquet. Cela a lieu quand on change d’unité dans l’ordonnée entre A et B, et donc peut s’exprimer ainsi (le abs car l’angle va de 0 à 360°) :

Enfin la dernière variable, buff, est elle aussi récursive - et est d’abord initialisée à 0 par nb. C’est juste un compteur qui indique le nombre de lancers pour lesquels l’aiguille coupe une lame de parquet.

Reste à définir l’estimation de Pi, dans une dernière variable, PiApp qui vaut simplement :

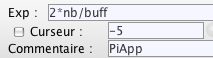
Bien-sûr avec cette simple définition, PiApp n’est pas définie au départ puisqu’il y a une forme indéterminée due à la division par 0.

On a ajouté une distinction visuelle entre les segments qui coupent et ceux qui ne coupent pas les lames de parquet. Pour cela le segment [AB] a une couleur par défaut (ici bleu clair) et prend la couleur rouge si coupe est égal à un.

Pour réaliser cela on fait un clic-droit sur le segment (même si un clic le fait changer de place, il est sélectionné dans l’inspecteur d’objet), on lui met une couleur par défaut de notre choix et dans l’onglet Conditionnel, on peut par exemple choisir ceci :

3. La figure ainsi réalisée

Il suffit de lancer la simulation par le bouton Marche/Arrêt.

<carmetal|doc=759|largeur=826|hauteur=516>

4. Ajout de l’évolution de la valeur approchée

Dans la figure suivante, on a repris la figure initiale, cette fois sans les 4 tests conditionnels pour placer A et B au départ, donc pour une utilisation en ligne, il vaut mieux commencer par un mini zoom à la souris pour tout effacer.

On se propose maintenant d’afficher l’évolution de l’approximation, par tranche de mille, à partir de mille. Pour cela on définit :

La tranche des milliers
Par la variable mil qui vaut tout simplement floor(nb/1000)
Le reste de la division par 1000
dans une variable abs1 qui vaut : if(mil==0 ;0 ;nb-mil*1000)
car on n’affichera le résultat qu’à partir de 1000 lancers (à cause de l’échelle choisie)

Puis en choisissant un repère adéquat (et 1 unité pour 1/10), on va afficher la trace d’un point Aff de coordonnées :

Le test est pour n’afficher qu’à partir de 1000 lancers (sinon abs1 est nul). Le reste est une question d’échelle : on affiche ici 1000 traces du point sur une longueur de 10 unités. Dans la figure suivante on a choisi de mettre les traces en gras, mais c’est modifiable après téléchargement.

Enfin pour y voir quelque chose, sur les 10 premiers groupes de 1000 lancers on a choisi des couleurs différentes, dans l’onglet conditionnel du point Aff :

Bien-sûr tout cet environnement ralenti un peu les tirages mais avec plusieurs Maj-Flèche droite successifs on arrive à une vitesse permettant de voir rapidement plus de 10000 lancers.

5. La figure correspondante

<carmetal|doc=764|largeur=826|hauteur=516>

6. Quelques remarques

Cet exercice de simulation montre tout d’abord l’efficacité de faire se rencontrer des traces d’objets et la récursivité : on n’utilise en définitive qu’un seul segment que l’on relance des milliers de fois, comme on le ferait dans un langage de programmation ordinaire.

Bien entendu, cette simulation dans un logiciel de géométrie dynamique n’a plus rien de dynamique, au sens où il n’y a pas du tout de manipulation directe : ce n’est qu’une simulation de tirages statistiques. Le logiciel est plus utilisé ici comme interface graphique de simulation d’un programme, réparti, lui, sur quelques variables récursives.

On notera toutefois l’utilisation de ses ressources internes comme les couleurs conditionnelles des traces qui rendent la simulation plus sympathique.

L’ancien prof de maths, formé dans sa jeunesse à optimiser la mémoire et ses lignes de calcul, reste assez bluffé que tous ces calculs supplémentaires - les 4 tests sur A et B pour éviter que l’animation ne démarre trop vite en ligne, et tous les autres ajoutés à partir du point 4 - ne ralentissent pas vraiment l’animation : elle est suffisamment rapide pour être utilisable. Décidément les processeurs sont bien rapides ;-)