L’origine du papillon de Lorenz

En 1962, Edward Norton Lorenz publie dans le Journal of Atmospheric Sciences un article sur les systèmes de flux hydrodynamiques dissipatifs. Il y présente alors un modèle d’atmosphère basé sur une simplification extrême des équations de Navier-Stokes [1]. Il utilise ensuite le nombre de Rayleigh qui caractérise le passage de la conduction à la convection, afin d’obtenir les constantes correspondantes à un écoulement turbulent.

L’article de cet illustre professeur sur lequel est basé mon travail est disponible à la lecture en anglais en cliquant ici.

Ce processus de simplification des équations par discrétisation de l’espace sous la forme de petites cellules de convection offre l’avantage de pouvoir être facilement calculable numériquement. Ce que Lorenz a fait dans les années 60 sur son ordinateur : un Royal McBee LGP-300.

Pour mieux visualiser cette atmosphère modélisée, il décida de se placer dans l’espace des phases (ou états du système) en utilisant la méthode qu’Henri Poincaré avait mise au point pour étudier les systèmes dynamiques.

En 1972, Edward Lorenz propose ce titre original pour sa conférence sur la modélisation de l’atmosphère :
Le battement d’ailes d’un papillon au Brésil peut-il provoquer une tornade au Texas ?

C’est l’origine du fameux « Effet papillon », qui résume métaphoriquement cet important phénomène de sensibilité aux conditions initiales qui est présent au cœur même du chaos.

Pour en savoir plus, je vous conseille l’excellente vidéo en français réalisée par David Louapre sur sa chaîne Science étonnante qui crée des ponts avec mon article précédent sur la suite logistique.

Coder le système dynamique de Lorenz

Lorenz se place dans un espace contenant trois variables indépendantes x, y et z qui sont liées dynamiquement, c’est-à-dire dans le temps, par un système d’équations différentielles (pour s’aider à le visualiser, on pourrait très naïvement s’imaginer que x représente, par exemple, la température, y la pression et z les échanges avec l’océan).

Une proposition de modélisation d’atmosphère ultra simplifiée : l’équation de Lorenz

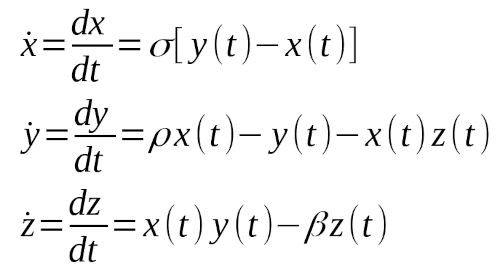
Lorenz propose d’utiliser les valeurs sigma=s=10 ; rho=r=28 et beta=b=2.667 pour les constantes afin d’obtenir un système convectif. La fonction s’implémente très directement en Python :

def lorenz(x, y, z, s=10, r=28, b=2.667):
    """Calcul des dérivées de Lorenz par rapport au temps"""
    x_point = s*(y - x)
    y_point = r*x - y - x*z
    z_point = x*y - b*z
    return x_point, y_point, z_point

Il existe en Python une méthode très élégante pour générer des listes de nombres tout en économisant de la mémoire et en simplifiant l’écriture : les générateurs Python qui utilisent le mot clé yield.

def lorenz_gen(x0, y0, z0):
    """Un générateur Python des états successifs de Lorenz"""
    x=x0
    y=y0
    z=z0
    dt = 0.01
    while (True) :
        # C'est un générateur Python infini qui
        # stoppe après yield et reprend au prochain appel next
        yield x,y,z
        # On applique les équations de Lorenz
        x_point, y_point, z_point = lorenz(x,y,z)
        # On calcule l'état suivant pour X, Y, Z grâce à EULER
        x = x + x_point * dt
        y = y + y_point * dt
        z = z + z_point * dt

Il est maintenant possible de générer les positions successives dans l’espace des phases avec ce code :

X0 = 0.
Y0 = 1.
Z0 = 3.
position = iter(lorenz_gen(X0,Y0,Z0))

for i in range(0,5) :
    print(next(position))

Le code complet ci-dessus est téléchargeable sur github en cliquant ici.

L’exécution du code ci-dessus nous donne pour chaque ligne les coordonnées x,y,z correspondant à l’état de notre système « atmosphèrique » à chaque instant dt :

(0.0, 1.0, 3.0)
(0.1, 0.99, 2.91999)
(0.189, 1.00518001, 2.8431038667)
(0.270618001, 1.0426747435919368, 2.769178076794011)
(0.34782367525919367, 1.1005271420804672, 2.698145763033955)

Visualiser en 3D avec matplotlib

Pour visualiser en trois dimensions, il faut importer la librairie Axes3D du toolkit de matplotlib :

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

On réutilise le code de la fonction de Lorenz et son générateur vus au chapitre précédent afin de calculer un nombre NbPasMax positions tous les intervalles de temps dt :

NbPasMax = 10000
xs=[]
ys=[]
zs=[]
position = iter(lorenz_gen(X0,Y0,Z0))

for i in range(0,NbPasMax) :
    x,y,z = next(position)
    xs.append(x)
    ys.append(y)
    zs.append(z)

On initialise la figure matplotlib, on précise que l’on veut une courbe en trois dimensions et on légende le tout avant de tracer la courbe que l’on affiche :

fig = plt.figure()
ax = plt.axes(projection='3d')

ax.set_xlabel("Axes des X")
ax.set_ylabel("Axes des Y")
ax.set_zlabel("Axes des Z")
ax.set_title("Attracteurs étranges du Papillon de Lorenz")

ax.plot(xs, ys, zs, lw=0.5)
plt.show()

Le code complet ci-dessus est téléchargeable sur github en cliquant ici.

La forme de papillon de cette courbe 3D est caractéristique, c’est le fameux papillon de Lorenz. On remarque que les courbes s’enveloppent sans jamais se croiser tout en « orbitant » autour des deux attracteurs dit « étranges » car leur structure est fractale.

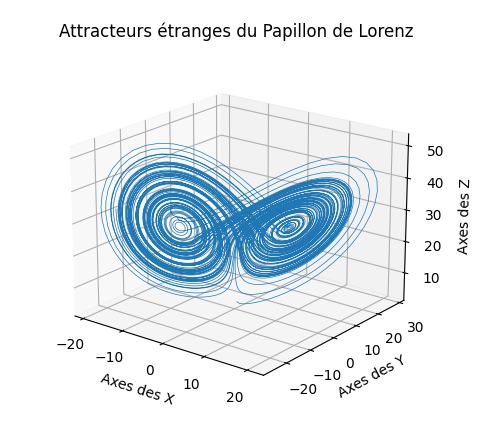
Si vous visualisez cet article en vous accompagnant d’une fenêtre Jupiter, je vous conseille de taper : %matplotlib pour bénéficier d’une fenêtre indépendante qui vous permettra d’utiliser la souris pour tourner en temps réel autour de la courbe en 3D.

La sensibilité aux conditions initiales

Dans l’excellent livre de James Gleick : La Théorie du Chaos, l’auteur précise :

« Un jour d’hiver 1961, désirant examiner une de ses séquences sur une plus longue période, Lorenz prit un raccourci. Au lieu de reprendre au début l’exécution de son programme, il commença à mi-chemin. » [2]

Lorenz prit ses nouvelles conditions initiales à partir des nombres du listage précédent et il observa que la suite générée divergeait très rapidement par rapport aux précédentes.

« Sa première réaction fut qu’un tube à vide de son ordinateur avait encore flanché. Soudain, il comprit la vérité. Tout avait bien fonctionné. Le problème se trouvait dans les nombres qu’il avait tapés. L’ordinateur gardait en mémoire des nombres à six chiffres, par exemple 0,506127, dont trois décimales seulement : 506 apparaissaient à l’impression, pour économiser de la place. » [3]

Il avait tapé sur le clavier de son ordinateur des conditions initiales tronquées au millième. C’est-à-dire des conditions initiales très légèrement différentes du listage précédent. Ce n’était pas évident pour l’époque : il découvrait que le déterminisme peut donner des résultats imprévisibles au bout d’un temps assez court, car il est impossible d’avoir une précision infinie pour les valeurs des conditions initiales.

Lorenz lui-même déclare :

« L’homme de la rue qui voit que l’on peut prédire relativement bien les marées sur quelques mois demandera pourquoi nous ne pouvons en faire autant avec l’atmosphère ; ce n’est qu’un fluide différent et ses lois sont tout aussi compliquées. Mais j’ai réalisé que tout système physique ayant un comportement non périodique était imprévisible. » [4]

Animer une fenêtre plplot pour visualiser l’influence des conditions initiales

Le système de Lorenz est un système dynamique : les trois coordonnées x,y,z dépendent du temps, elles sont donc parfaitement adaptées pour une animation en fonction du temps.

Matplotlib est capable de gérer des animations. Pour cela, il faut importer la librairie animation :

import matplotlib.pyplot as plt
import matplotlib.animation as animation

La méthode de visualisation la plus simple revient à observer l’évolution au cours du calcul de deux trajectoires de Lorenz ayant des conditions initiales identiques à epsilon près. Pour simplifier, on se placera en 2D et je ne proposerai dans le corps de cet article que le code nécessaire pour une unique trajectoire. Et on récupérera le code de la fonction de Lorenz et son générateur vus au deuxième chapitre.

X0 = 0.
Y0 = 1.
Z0 = 3.
DT = 0.01
EPSILONX = 0.01

x1s=[]
y1s=[]
x1s.append(X0)
y1s.append(Y0)

Objet1position = iter(lorenz_gen(X0,Y0,Z0,DT))

Pour le second objet, il suffit, à l’initialisation, d’ajouter une valeur epsilon à l’une des conditions initiales :

Objet2position = iter(lorenz_gen(X0+EPSILONX,Y0,Z0,DT))

On initialise la fenêtre plplot en mode objet, on fixe les axes, on affiche la légende, on initialise un point mouvant rouge le long d’une trajectoire représentée par une ligne elle même rouge :

fig, ax = plt.subplots()
ax = plt.axis([-25,30,-30,30])
ax = plt.title("Trajectoires de Lorenz XY: Papillon en 2D")
ax = plt.xlabel("X")
ax = plt.ylabel("Y")

pointRouge, = plt.plot(X0, Y0, 'ro')
trajectoireRouge, = plt.plot(x1s, y1s, 'r-')

À cette étape, on va créer une fonction fondamentale : la fonction animate(frame) qui va se lancer automatiquement et périodiquement afin de calculer, image après image l’animation qui va s’afficher dans la fenêtre.

def animate(frame):
    x1,y1,z1 = next(Objet1position)
    x1s.append(x1)
    y1s.append(y1)

    trajectoireRouge.set_data(x1s,y1s)
    pointRouge.set_data(x1,y1)
    return trajectoireRouge, pointRouge,

On génère l’animation en utilisant la fonction animation.FuncAnimation() qui possède de nombreuses options très pratiques. Il faut absolument afficher la fenêtre plt après l’initialisation de l’animation pour que cela fonctionne.

# créer une animation en utilisant la fonction animate()
myAnimation = animation.FuncAnimation(fig, animate, frames=1300, interval=30, blit=True, repeat=True)

plt.show()

Le code complet ci-dessus est téléchargeable sur github en cliquant ici.

On observe sur l’animation ci-dessus qu’au départ, les deux trajectoires sont parfaitement confondues et les points rouge et bleu suivent exactement le même chemin puis, petit à petit, ils se séparent doucement tout en se poursuivant avant de sombrer dans le chaos en suivant des trajectoires complètement différentes : c’est une visualisation de l’influence des conditions initiales sur la prédictibilité des systèmes dynamiques.

Enregistrer des animations de haute qualité en .gif ou en mp4

Il est possible d’améliorer très nettement la qualité de l’image obtenue lors de l’animation en augmentant le nombre de points par pouce (dpi = dot per inch) lors de l’initialisation de l’objet figure de matplotlib ce qui correspond à la résolution de la « feuille de dessin » :

fig = plt.figure(dpi=200)

L’animation .gif du chapitre précédent s’obtient très facilement en rajoutant le code suivant :

 myAnimation.save('Lorenz2DXY.gif', writer='imagemagick')

L’animation est enregistrée à vitesse de calcul maximale directement sur le disque dur sous la forme d’un fichier .gif sans rien afficher à l’écran lors de l’exécution. Les fichiers obtenus sont un peu obèses et peuvent être optimisés en utilisant un utilitaire externe : j’ai personnellement utilisé un logiciel en ligne de commande Bash : gifsicle qui est très efficace et rapide afin de passer en dessous d’une limite de 2Mo pour la taille des fichiers :

$ gifsicle -b -O3 --colors 4 Lorenz2DXY.gif

Il est tout aussi facile de générer des fichiers vidéos en .mp4 en utilisant le code Python suivant :

myAnimation.save(r'MonAnimation.mp4')

La beauté cachée du système dynamique de Lorenz

Avec un système aussi intéressant, il est possible de générer de très belles animations en 3D ainsi que de magnifiques projections en 2D. Je vous propose de générer une grille cubique de « particules ». Elles suivent chacune une trajectoire différente du système de Lorenz. On affiche toutes les positions de ces « particules » à chaque instant dt, puis on projette en 2D. Cela donne l’animation ci-dessous :

On peut visualiser la même chose en 3D en tournant doucement autour de notre courbe grâce au code suivant rajouté dans la fonction update(num) :

ax.view_init(20,num)  # Rotation autour de la figure sur le plan XY

La qualité de la vidéo ci-dessous peut être ruinée par les algorithmes de compression de YouTube. N’hésitez pas à choisir la meilleure résolution HD sous YouTube ou bien générez la vidéo par vous-même pour une qualité quasi-parfaite.

Le code complet ci-dessus est téléchargeable sur github en cliquant ici.

On peut aussi, avec beaucoup de calculs et de temps, générer une animation vidéo pour un très grand nombre de particules ayant des conditions initiales extrêmement proches ( dans ce cas il y a 33 334 Trajectoires sur 2000 pas de temps avec des écarts EPSILON = 0.00005 ) :

Le code complet ci-dessus est téléchargeable sur github en cliquant ici.
En utilisant d’autres librairies de rendu et des temps de calcul beaucoup plus importants, il est possible d’obtenir de magnifiques animations comme celle-ci en utilisant exactement les mêmes principes.

Si on colore chaque trajectoire différemment, on obtient ceci :

Le code complet ci-dessus est téléchargeable sur github en cliquant ici.

On commence à observer les limites de la librairie matplotlib Axes3D car l’occultation des lignes en fonction du « zbuffer » n’est pas prise en compte...

Conclusion

Les travaux de Lorenz nous font profondément réfléchir sur notre capacité à prédire l’avenir par la science. Même si toutes les formules que nous connaissons étaient parfaitement exactes, notre incapacité fondamentale à mesurer les conditions initiales avec une précision infinie implique qu’il nous sera à jamais impossible de prédire l’avenir !

Ce type de chaos est presque partout présent dans la nature qui nous entoure : dans les rivières et les nuages, dans les vents et les courants, convectifs et turbulents.

Il est même possible de fabriquer un système physique réel (un véritable circuit électrique) pour visualiser le Papillon de Lorenz sur un oscilloscope comme le propose cette vidéo

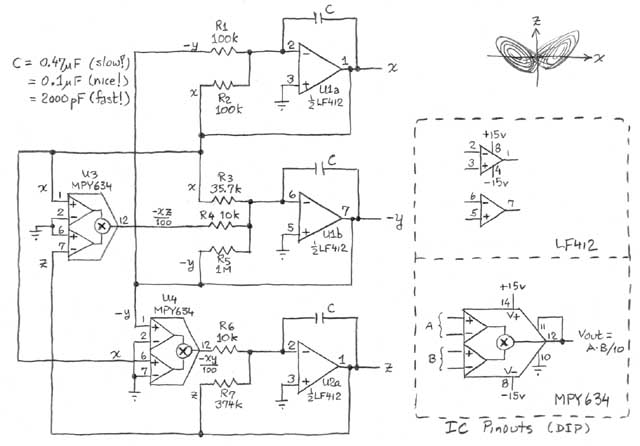
Il y a encore de nombreuses connaissances à acquérir sur le système dynamique de Lorenz. Jos Leys, Étienne Ghys et Aurélien Alvarez ont réalisé un fantastique documentaire en neuf chapitres de treize minutes chacun sous licence libre : CHAOS : UNE AVENTURE MATHÉMATIQUE.

Ce documentaire est accessible en français et le visionner devrait être la prochaine étape de votre voyage dans les contrées étranges du chaos mathématique et naturel.

L’excellent article d’Étienne Ghys pour le séminaire Poincaré XIV de 2010 : L’attracteur de Lorenz, paradigme du chaos est consultable en cliquant ici.