<freemind|doc=499|largeur=450|hauteur=200>
REMERCIEMENTS :
– Merci à l’équipe de Tracenpoche pour leur activité (visualisation en géométrie dynamique).
– Merci à la fondation M.C. Escher pour l’autorisation de publier une image de son oeuvre (cascade).
– Un grand merci à Wikimedia Commons pour toutes ces images libres qui m’ont permis de faire le paragraphe historique sur la vie de Thalès de Milet.
– Merci à Sylvie Almeida pour l’image publiée en couverture de Sciences et vie Junior (drôle de triangle).
– Merci à Techno-Sciences et à leur encyclopédie en ligne qui m’a permis de réaliser le paragraphe sur la triangulation.
– Merci à l’équipe de Sésamath pour leurs excellents cahiers Mathenpoche.
1. Activité de découverte
Télécharger la fiche élève :
2. Visualisation en géométrie dynamique
Sur la figure suivante, déplacer les points A, B et C pour constater que la somme des angles du triangle ABC est toujours égale à 180° :
3. Un peu d’histoire
La propriété « La somme des angles d’un triangle est de 180 degrés » a été découverte par Thalès, qui a vécu à Milet (en Turquie) de 620 à 550 avant J.-C.

|

|

|

|

|

|
Thalès était mathématicien, philosophe et astronome. C’est l’un des fondateurs des mathématiques grecques. On lui doit de nombreuses découvertes comme celle des planètes dans notre système solaire.
4. Angles et art
Cliquer sur une image pour l’agrandir :

La cascade de M.C. Escher
|
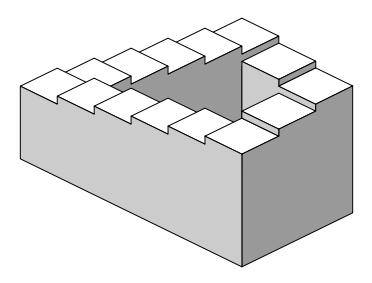
L’escalier impossible
|

Un drôle de triangle
|
5. Application à la triangulation
I. Calcul de la distance d’un bateau en mer à la côte
Thalès mit au point une méthode pour évaluer la distance d’un bateau en mer à la côte. Cette méthode, appelée la TRIANGULATION, utilise (entre autre) la propriété de la somme des angles d’un triangle qui vaut 180 degrés.
Pour avoir une mesure approximative de cette distance, Thalès plaça deux observateurs A et C sur le rivage, éloignés d’une distance b connue. Il demanda à chacun d’entre eux de mesurer l’angle que font les droites passant par le bateau B et l’un d’entre eux, et la droite passant par les deux observateurs.
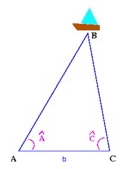
La méthode a un intérêt si nous voulons déterminer de grandes distances ; mais, dans ce cas, nous devons placer les deux observateurs suffisamment éloignés l’un de l’autre, pour que les mesures d’angle soient plus précises.
II. Navigation par relèvement à un amer
Jusque dans les années 1980, on utilisait essentiellement la triangulation pour mesurer les distances. Si l’on veut mesurer la distance entre deux points B et C, l’opération consiste à prendre un point de référence A, puis de mesurer les angles que font les droites (AB) et (AC) par rapport au Nord indiqué par une boussole ce qui donne l’angle $\widehat{BAC}.$
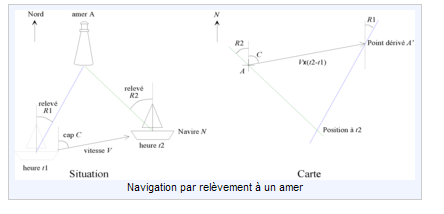
III. Cartographie de la France
Ce procédé de triangulation, répété de proche en proche, a été utilisé par Delambre et Méchain de 1792 à 1798 pour mesurer la distance entre Dunkerque et Barcelone (environ 1147 km) sur le méridien de Paris, ce qui permit la première définition du mètre en 1799.

6. Exercices
Télécharger la feuille d’exercices :

Commentaires