Simulation de variables aléatoires normales

mardi 23 avril 2013
par  Alain BUSSER

La calculatrice autorisée au bac sait simuler des variables pseudo-aléatoires uniformes sur [0 ;1[ ; il est aisé de simuler à partir de celle-ci, avec la méthode de la transformée inverse, une loi exponentielle. Mais pour manipuler des variables normales, il est nécessaire de les simuler. Plusieurs algorithmes sont utilisables en Terminale, tant qu’on ne cherche pas à y démontrer leur validité...

I/ À partir de variables binomiales

Le théorème de Moivre-Laplace permet de calculer une variable presque normale, avec une variable binomiale de paramètres N et 0,5 où N est grand (typiquement quelques dizaines). C’est la méthode utilisée dans MathsOntologie ; elle est peu efficace parce qu’elle fait appel à une boucle sur le nombre de boules à tirer (avec remise) de l’urne, et cette boucle doit être parcourue un grand nombre de fois. De plus, elle ne donne que des entiers, ce qui, même après avoir centré et réduit, se voit à l’affichage du résultat (et en plus, celui-ci est borné).

Remarques épistémologiques

Comme son nom l’indique, le théorème de Moivre-Laplace a été découvert par Abraham de Moivre au début du siècle des lumières, dans le cas p=0,5. À la fin du même siècle, Pierre-Simon de Laplace redémontre le même théorème, mais pour tout p∈[0 ;1], avec des transformées de Laplace. En fait, Laplace fait mieux que démontrer le théorème portant son nom : Il en fait le corollaire d’un théorème plus général, le théorème central-limite, qui dit en substance ceci :

Quand on additionne un grand nombre de variables aléatoires indépendantes entre elles, le résultat est normal.

Ce théorème [1] explique pourquoi on voit des lois normales partout : Par exemple, les phénotypes résultent souvent de l’action combinée de plusieurs gènes et si ces actions sont indépendantes, les phénotypes en question deviennent normaux.

Le théorème de Moivre-Laplace dit ceci :

Une variable binomiale de paramètre N grand et de paramètre p voisin de 0,5 est bien approchée par une loi normale.

Or, une variable binomiale est somme de variables de Bernoulli (compter, c’est additionner des 0 ou des 1) indépendantes entre elles, et le théorème central-limite est donc bien une généralisation du théorème de Moivre-Laplace.

Dans le programme mis en place pour le bac 2013, la loi normale est définie comme limite de lois binomiales en ES/L et en S ; mais il n’en est pas de même dans les sections technologiques STI2D/STL, où la loi normale est définie ainsi :

La loi normale est introduite à partir de
l’observation, à l’aide d’un logiciel, du cumul
des valeurs obtenues lors de la répétition à
l’identique d’une expérience aléatoire dont le
résultat suit une loi uniforme.

et plus précisément :

On peut simuler une loi normale à partir de la
loi uniforme sur [0,1] .

Ce qui suggère l’algorithme suivant :

II/ Par addition de variables uniformes

La somme de n variables uniformes sur [0 ;1] suit une loi Irwin-Hall de paramètre n [2]. Comme celle-ci est rapidement proche d’une variable normale, on peut donc simuler une variable normale par la somme de n variables uniformes sur [0 ;1]. Ce qui donne lieu au TP suivant (de moins d’une heure) sur la calculatrice (ti 82 stats fr ci-dessous) :

  1. on constate que Suite(NbrAléat,K,1,12) donne 12 nombres uniformes sur [0 ;1] (présentés comme les résultats de mesures par des tricheurs qui préfèrent inventer des nombres au hasard que de faire la mesure) ;
  2. on imbrique cela dans un somme pour obtenir la somme des 12 nombres (présentée comme le résultat d’un travail collaboratif des 12 tricheurs) : on a Somme(Suite(NbrAléat,K,1,12))
  3. on constate après quelques essais que la loi n’est pas uniforme sur [0 ;12] puisqu’aucun élève n’a eu, même après plusieurs répétitions, de nombre inférieur à 2.
  4. On vérifie avec une boucle sur I allant de 1 à 100 : 
    :For(I,1,100,1)
:Somme(Suite(NbrAléat,K,1,12))→L1(I)
:End

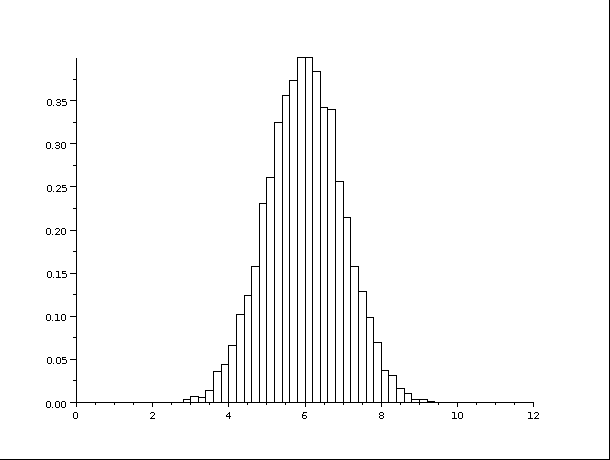
    Après quelques minutes, L1 contient un échantillon de 100 telles valeurs ; on met l’un des affichages statistiques sur « on », on le met en mode « histogramme » et on paramètre la fenêtre de façon à voir l’histogramme.

L’histogramme ressemble typiquement à ceci (avec Xgrad=0.5) :

version Scilab

L’algorithme est aisément transposable à Scilab :

liste=zeros(1,10000)
for i=1:10000
  liste(i)=sum(rand(1,12))
end
clf
histplot(0:0.2:12,liste)

l’affichage, plus précis que la calculatrice, vient en une fraction de seconde :

Pourquoi douze termes ?

On a vu en cours que la variance d’une loi uniforme sur [0 ;1] est 1/12. Comme par ailleurs, la somme de variables aléatoires indépendantes [3] a pour variance, la somme de leurs variances, en additionnant 12 variables uniformes sur [0 ;1] on obtient une variable aléatoire de variance 1, donc réduite. Il suffit alors de soustraire son espérance 6 pour qu’elle soit également centrée.

test de normalité version Χ2

Pour recréer l’histogramme dans R, on peut créer les données comme avec la calculatrice :

donnees <- NULL
for (n in 1:10000){
  donnees <- c(donnees,sum(runif(12,0,1)))
}

Un histogramme à classes de même largeur se fait avec

histo <- hist(donnees, breaks = seq(0,12,0.25), freq = FALSE, right = FALSE)
grid()
abscissesX <- seq(0, 12, length = 1000)

On a ce genre d’histogramme :

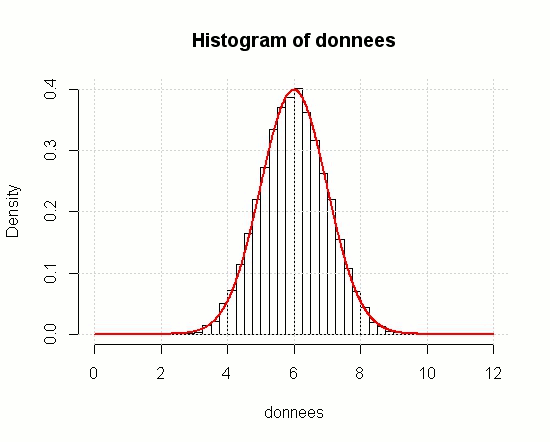
Et en ajoutant la représentation graphique d’une loi normale de paramètres 6 et 1, en rouge :

lines(abscissesX, dnorm(abscissesX, 6,1), col = "red", lwd = 2)

on obtient ceci :

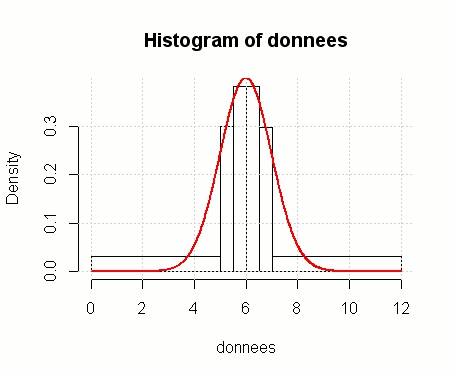
Ces données ne sont pas adaptées à un test de Khi-deux, parce que les effectifs sont mal répartis. Pour y remédier, on peut faire un histogramme à classes presque équiréparties :

subdiv <- c(0,seq(5,7,0.5))
subdiv <- c(subdiv,12)

histo <- hist(donnees, breaks = subdiv, freq = FALSE, right = FALSE)

On obtient alors ceci :

Il n’y a maintenant plus que 6 classes, donc en supposant que μ=6 et σ=1, il reste 4 degrés de liberté ; on construit la liste des effectifs :

mu <- 6
sigma <- 1

Nsub <- length(subdiv)
EffTheo <- NULL
for(i in 1:(Nsub - 1)){
  EffTheo <- c(EffTheo,
               (pnorm(histo$breaks[i + 1], mu, sigma) - pnorm(histo$breaks[i], mu, sigma)) * length(donnees))
}

puis le critère de Χ2 :

(criterium <-  sum((histo$counts - EffTheo)^2 / EffTheo))
pchisq(criterium, length(histo$counts) - 2, lower.tail = FALSE)

R fournit alors la probabilité critique, qui dans le cas présent vaut environ 0,07 : On prend environ 7% de risque en admettant que la loi est normale de paramètres 6 et 1 [4]

Test de Shapiro

L’aide en ligne du logiciel R recommande, pour tester la normalité d’une variable aléatoire, le test de Shapiro-Wilk.

Avec le premier des histogrammes ci-dessus, il suffit d’entrer

shapiro.test(donnees)

et R répond que la « p.value » est 0,05425 et on prend un risque d’environ 5% à affirmer que la loi est normale [5].

Suite du TP : On demande de rappeler les limites de x2 en -∞ et en +∞ et on demande par quoi composer x2 pour que l’axe des abscisses soit asymptote deux fois. Puis on constate que le maximum est atteint en 6 si on prend e-(x-6)2/2 (le quotient par 2 est admis), et on demande de déterminer empiriquement par combien on doit multiplier cette fonction pour l’ajuster à l’histogramme...

III/ Algorithme de Box-Muller

La méthode de Box-Muller est spécifique aux variables normales centrées réduites. Elle est basée sur le principe suivant :

  • Au lieu de considérer une variable aléatoire normale centrée réduite X, on en considère deux, X et Y, indépendantes entre elles ;
  • X et Y sont alors considérés comme les coordonnées d’un vecteur ;
  • la norme de ce vecteur suit une loi de Rayleigh ;
  • donc son carré suit une loi exponentielle ;
  • et l’angle vecteur de (X,Y) suit une loi uniforme sur [0 ;2π]
  • On reprend donc le problème à l’envers :
    • On simule une variable θ uniforme sur [0 ;2π] ;
    • On simule aussi une variable U uniforme sur [0 ;1] ;
    • -2 ln(U) suit alors une loi exponentielle de paramètre 0,5 ;
    • on calcule alors sa racine carrée r, qui suit donc une loi de Rayleigh de paramètre 0,5 ;
    • les variables r×cos(θ) et r×sin(θ) sont alors normales, centrées, réduites et statistiquement décorrélées.

Comme le montre le cours, GeoGebra utilise l’algorithme de Box-Muller.

Comparaison des performances

Pour calculer une variable normale centrée réduite, l’algorithme des douze termes utilise 12 appels à random, 12 sommations et une soustraction (de 6) ; alors que Box-Muller utilise 2 appels à random, un logarithme, une racine carrée et une fonction trigonométrique, avec une multiplication finale. Mais pour une deuxième variable normale, il suffit d’un sinus et une multiplication supplémentaires.

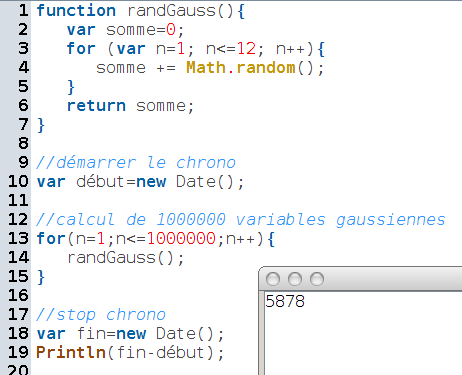
L’universalité de JavaScript [6] permet assez facilement de mesurer le temps (en millisecondes) qu’il faut pour calculer un million de variables gaussiennes avec l’approximation par une loi d’Irwin-Hall de paramètre 12 ; on trouve 5878 millisecondes pour 1000000 de calculs, donc environ 6 microseconde par calcul :

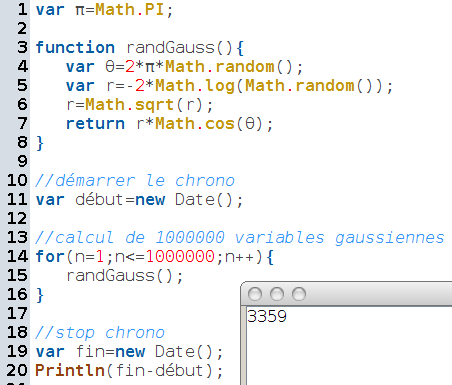
Alors qu’avec l’algorithme de Box-Muller, même sans calculer encore plus vite deux par deux avec le sinus, on trouve 3359 millisecondes pour 1000000 de calculs, soit environ 3,4 microseconde par calcul :

L’algorithme de Box-Muller est donc plus efficace que l’algorithme de la somme des douze [7].


[1] En fait il n’est pas valable pour des lois de Cauchy : il faut que les variables additionnées possèdent une espérance et une variance.

[2] Remarque : La somme de n variables exponentielles de paramètre λ indépendantes entre elles suit une loi d’Erlang de paramètres n et λ ; celle-ci converge également vers une loi normale lorsque n tend vers ∞, d’après le théorème central-limite. Mais c’est plus surprenant, les lois exponentielles étant fortement asymétriques.

[3] En fait, il suffit qu’elles soient statistiquement décorrélées ; comme elles sont calculées par une suite récurrente, elles ne sont pas du tout indépendantes. Mais elles sont décorrélées, c’est-à-dire que leur covariance est nulle.

[4] ce qu’elle n’est pas : C’est une loi d’Irvin-Hall, en particulier, elle est bornée !

[5] l’aide en ligne de R dit que la normalité est acceptée dès que la p.value est inférieure à 0,1.

[6] Avec CaRMetal dont la console est toujours un régal pour programmer.

[7] En tout cas, sur un Celeron 1,5 GHz.


Documents joints

PDF - 90.6 kio

Commentaires