Exemple
Voici un exercice numérique que l’on peut traiter au choix en Blockly/Sophus, Logo ou Scratch :
Un prix qui était initialement de 80 €, a augmenté de 15 % ; quel est le nouveau prix après augmentation ?
On utilisera une variable prix qui sera initialisée à 80 puis augmentée de 15 pourcents et enfin affichée.
Dans chacun des onglets suivants, on va aborder le même problème avec des outils différents, ce qui permet de mieux appréhender leur saveur.
Blockly
On utilisera bloquement, utilitaire en français de programmation Blockly doté d’un export automatique en JavaScript, et auquel a été intégré Sophus.
Pour commencer, on doit créer une variable prix mais celle-ci n’existe pas encore. Si on regarde le menu des variables, on constate qu’il y a en fait une variable virtuelle appelée element :

En glissant « fixer element à » sur le plan de travail (la zone blanche à côté du menu gris) on voit que le programme est né et ne demande qu’à grandir (ce qui se fera vers le bas). On voit également que le mot element est suivi d’un petit triangle, ce qui signifie qu’il y a un menu déroulant, comportant la liste des variables. On peut en créer une, que l’on nomme prix pour avoir ceci :
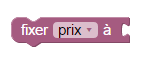
Reste à voir à quoi on va le fixer, ce prix. Ce n’est pas une variable que l’on va mettre ici, mais une constante égale à 80. Pour trouver les constantes, il faut aller voir du côté des mathématiques :

On choisit la constante 0 et on la glisse vers la droite du « fixer prix à » où il y a un espace permettant de le brancher. On en profite pour remplacer ce 0 par un 80, en cliquant dessus puis en utilisant le clavier :
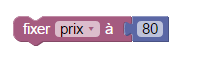
Voilà pour la première instruction de ce programme Blockly. Pour la suivante, on va utiliser la possibilité que permet Sophus, d’augmenter directement la variable prix de 15 pourcents. Voici le début du menu des pourcentages de Sophus :
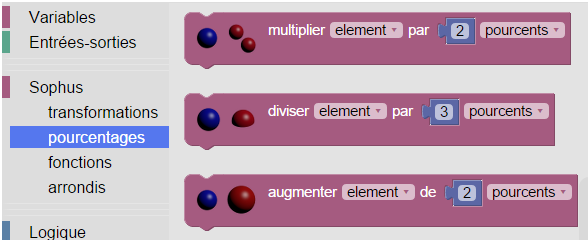
L’augmentation d’un certain pourcentage est la troisième de ces instructions. Par défaut elle permet d’augmenter de 2 pourcents la variable element. On doit donc choisir en lieu et place la variable prix, et remplacer 2 par 15 [1]. Si on branche le résultat obtenu en-dessous de l’instruction précédente, le programme Blockly est maintenant constitué de deux instructions :

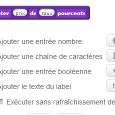
Ensuite, il reste à afficher le résultat ; l’affichage se trouve dans le menu des entrées-sorties :
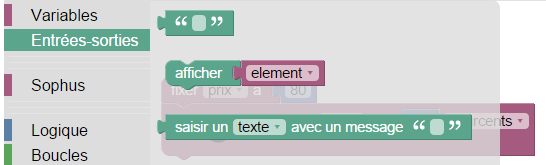
(on constate que ce menu est semi-transparent ce qui permet de deviner, en-dessous, le programme que l’on est en train de créer)
On branche en-dessous du reste, le second « afficher element » et l’on remplace element par prix, ce qui finit le programme :

Au fur et à mesure des manipulations, un programme JavaScript s’est rédigé dans le cadre de droite, et sa version finale est
var prix;
prix = 80;
prix = prix + prix * 15 / 100;
window.alert(prix);C’est en fait ce programme JavaScript qui est exécuté lorsqu’on clique sur le bouton « Lancer » en bas à gauche, ce qui a pour effet d’afficher une boîte de dialogue modale indiquant 92 : C’est bien le nouveau prix après augmentation de 15 %.
Logo
La tortue de Python permet de représenter l’augmentation de 15 pourcent par un déplacement de 15% de l’abscisse. Le script Python permettant de faire cela est
from turtle import *
forward(80)
forward(position()[0]*15/100)
print(position())Seulement le graphisme tortue de Blockly est minimal et ne permet pas, avec son menu actuel, de récupérer l’ordonnée (la tortue est tournée vers le haut) de la tortue par une des instructions disponibles. Alors on va utiliser Blockly et montrer comment fonctionne l’affichage particulier de la tortue. Le texte se faisant dans le sens de la tortue, il faut d’abord tourner celle-ci vers la droite pour que le texte soit lui aussi tourné vers la droite :
- tourner la tortue vers la droite ;
- cacher la tortue (pour qu’elle ne gêne pas la lisibilité du texte) ;
- initialiser le prix à 80 ;
- l’augmenter (« incrémenter ») de 15 pourcents de sa valeur ;
- l’afficher à la place de la tortue.
Le script ressemble à ceci :
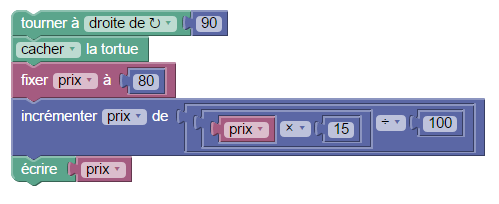
et a cet effet :

Remarque : On peut resserrer l’affichage du programme en effectuant sur chaque opération (multiplication et division) un clic droit suivi du choix de « Entrées externes » au lieu de « Entrées en ligne » ; l’effet est de remplacer l’écriture en ligne des expressions mathématiques, par un arbre syntaxique (tourné vers la droite) :
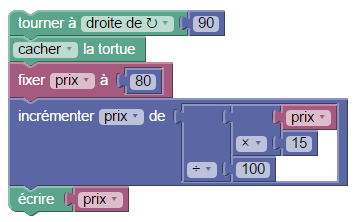
Blockly est donc un logiciel intéressant pour l’algèbre, puisqu’il permet le changement de cadre entre l’écriture en ligne et l’arbre syntaxique.
Scratch
Contrairement au Logo simplifié des jeux Blockly (voir onglet précédent), Scratch permet d’accéder pour chaque lutin, à des variables x et y qui sont ses coordonnées courantes. Donc là, on peut augmenter l’abscisse de 15 pourcents par un déplacement avec ce script :
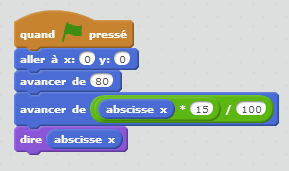
L’affichage se fait par l’intermédiaire du lutin qui est doté de la parole (et après on se demande pourquoi les « digital natives » sont si bavards en classe) :

Le résultat est correct, le nouveau prix est bien de 92 euros (ou plutôt, la nouvelle abscisse est de 92 pixels)...
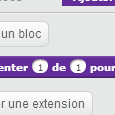
Scratch permet de définir ses propres blocs, grâce à la dernière option du menu, où figure « Ajouter blocs ». On choisit d’en ajouter un :
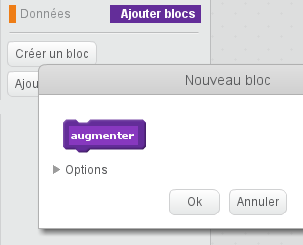
On y entre le texte « augmenter prix de » et on ouvre le menu des options :
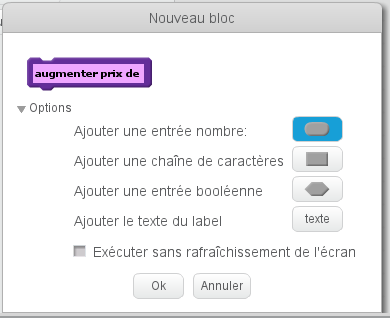
On constate qu’il est possible d’ajouter une variable (locale à la procédure) qu’on va appeler « taux » (avec « ajouter une entrée nombre ») :
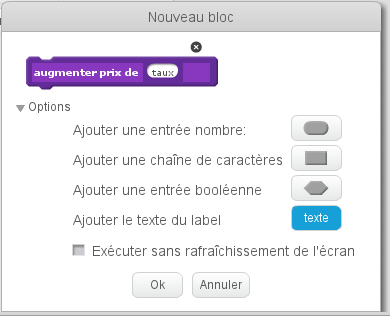
Dès lors, cette variable se manipulera comme les variables habituelles, en cliquant-glissant son nom pour en obtenir une copie. Ensuite on ajoute le texte « pourcents » :

En cliquant sur « OK », deux effets se font alors sentir :
- Une définition apparaît dans l’espace de travail :

- Le bloc en cours de création devient disponible dans le menu des blocs :

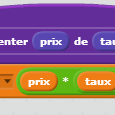
Pour programmer l’intérieur du bloc, on fait comme d’habitude avec Scratch : On « incrémente » la variable (globale on le rappelle, cela permet d’y accéder) « prix » du pourcentage, lequel se calcule par une multiplication par le taux et une division par 100 :
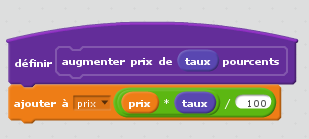
On remarque que la couleur des variables locales (bleu) n’est pas la même que celle des variables globales (orange).
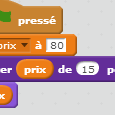
Ensuite, on peut utiliser ce bloc dans Scratch, en donnant à « prix » la valeur 80, puis en utilisant ce nouveau bloc pour l’augmenter de 15 pourcents et enfin, en affichant sa nouvelle valeur :

La vérité sort de la bouche des chatons :

En fait, tout cela peut être fait aussi avec la tortue de Blockly, et de la même manière :
Créer un bloc (avec cette syntaxe bizarre en français, « to » ayant été quelque peu rapidement traduit en « à » comme pour les boucles, au lieu de « pour ») :
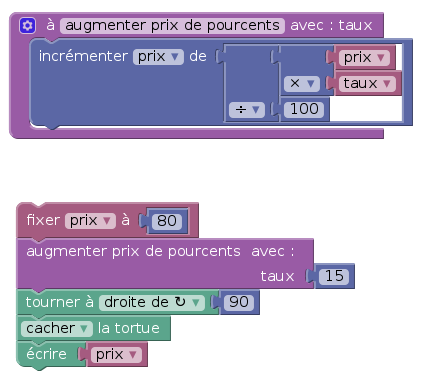
Ensuite, pour utiliser le bloc, il a été nécessaire de cacher la tortue après l’avoir fait tourner vers l’horizontale, afin qu’elle ne cache pas ce qu’elle a écrit et qu’on ne soit pas obligé de risquer le torticolis pour lire ce qu’a écrit la tortue : En effet, contrairement au chat qui sait parler, la tortue est muette, et se contente d’écrire par terre au milieu de ses gribouillis, lorsqu’elle a quelque chose à communiquer. La différence essentielle est que la tortue peut écrire des choses à divers endroits au gré de ses promenades, alors que la parole du chat suit le chat (on dirait du Yoda !).
La vérité sort de la bouche des tortues, ou plutôt du crayon qu’elles tiennent dans leur bouche :

En résumé, Scratch permet de définir des instructions mais pas des fonctions (qui retournent une valeur) ; au contraire, Blockly permet de définir soit des fonctions, soit des instructions, mais dans sa version de base, les variables sont toutes globales. Aussi est-ce Blockly qui a été choisi pour incorporer Sophus, mais pas sous la forme de « blocs utilisateur » : En construisant les blocs directement en JavaScript, avec la méthode exposée ici.
Sophus peut très bien s’inscrire dans une séquence pédagogique partant de déplacements successifs et allant vers les équivalents numériques. Par exemple pour savoir combien font 30-(-20) (soustraction des relatifs) on peut commencer par la tortue et ensuite transformer son abscisse seule avec Sophus.
La version Logo suggère que la nouvelle ordonnée de la tortue est 50 et donc que 30-(-20)=50 :
Elle a été obtenue avec le script suivant :

La version Sophus ressemble pas mal :
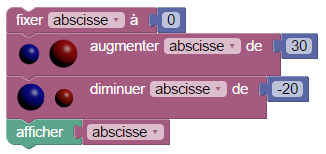
En fait elle produit ce script :
var abscisse;
abscisse = 0;
abscisse = abscisse + 30;
abscisse = abscisse - -20;
window.alert(abscisse);Ce qui peut amener à du JavaScript plus simple :
alert(30-(-20))
ou à l’utilisation de la calculatrice...
Voici maintenant une série d’exercices basés sur des programmes de calcul ou des algorithmes numériques avec leur solution programmée en Blockly sous bloquement.
- Dans l’onglet « listes de prix » on voit comment créer une liste dans Blockly.
- Dans l’onglet « fractions » on voit comment on peut créer son propre bloc en Blockly
Lynx
Voici un sujet des « jeux mathématiques du Monde » (n° 226, 5 juin 2001) :
Dans la forêt enchantée, 5 000 lapins vivaient heureux jusqu’au jour où arriva un couple de lynx.
Or, chaque lynx mange un lapin par jour !
Croyant bien faire, Merlin dota ces animaux d’un pouvoir de reproduction magique : chaque jour, après le repas des « fauves », chaque lapin donnerait naissance à deux nouveaux lapins, tandis que chaque lynx ne donnerait naissance qu’à un seul lynx.
Pour étudier l’évolution à long terme de la population de lapins, on peut déjà boucler 10 fois pour voir où on en est au bout de 10 jours ; avec ces traductions :
| énoncé | Sophus |
| chaque lynx mange un lapin par jour | diminuer lapins de lynx |
| chaque lapin donnerait naissance à deux nouveaux lapins | tripler lapins |
| chaque lynx ne donnerait naissance qu’à un seul lynx | doubler lynx |
Ce qui donne ce script :

Brevet
Voici un extrait du sujet de brevet « Centres étrangers (Maroc) 2015 », avec deux programmes de calcul :
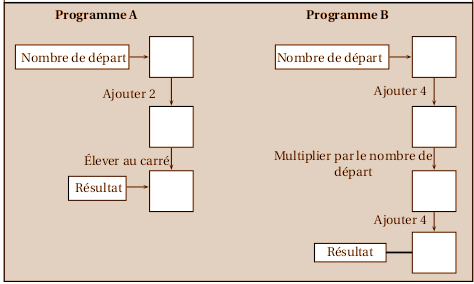
Le programme A ne pose aucun problème en Sophus :
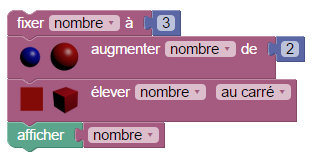
Mais le programme B lui, pose un problème avec l’instruction « Multiplier par le nombre de départ » : En version « 100% Sophus », le nombre de départ a été modifié entre-temps et doit donc être mémorisé avant ses modifications, sous la forme d’une copie :

La première question du sujet était
Montrer que si on choisit 3 comme nombre de départ, les deux programmes donnent 25 comme résultat
Les scripts ci-dessus y répondent pour les fanas du raisonnement inductif. La seconde question était :
Avec le programme A, quel nombre faut-il choisir au départ pour que le résultat obtenu soit 0 ?
Là on peut opérer par tâtonnement, en remplaçant le 3 de la première ligne par d’autres valeurs et en regardant ce qu’on obtient. Mais sans forcément garantir l’exhaustivité de la recherche de solution...
Magicien
Voici un extrait de l’exercice « spécialité » du bac S Polynésie 2014 :
Lors d’une représentation, un magicien demande aux spectateurs d’effectuer le programme de calcul (A) suivant :
« Prenez le numéro de votre jour de naissance et multipliez-le par 12. Prenez le numéro de votre mois de naissance et multipliez-le par 37. Ajoutez les deux nombres obtenus. Je pourrai alors vous donner la date de votre anniversaire ».
Un spectateur annonce 308 et en quelques secondes, le magicien déclare : « Votre anniversaire tombe le 1er août ! »
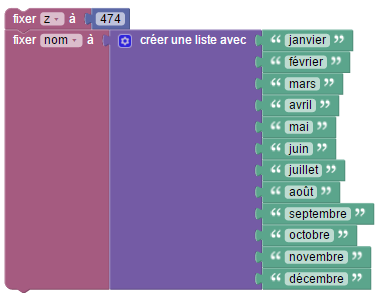
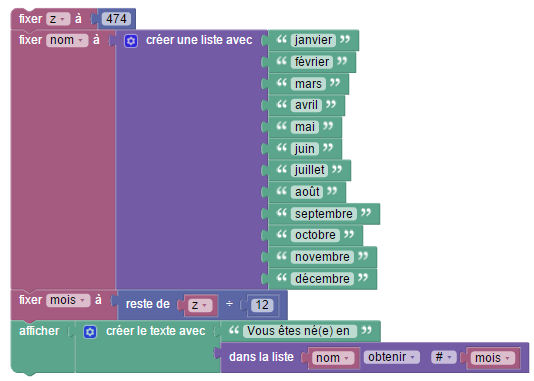
Tout d’abord, on va modéliser par un programme de calcul, ce qui se passe dans la tête d’un spectateur né le 21 juin :

En fait, rien ne sert de faire des calculs à moins que, comme le magicien a oublié de le demander, le « spectateur annonce 308 » :
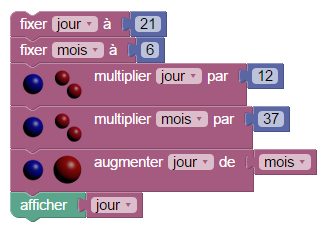
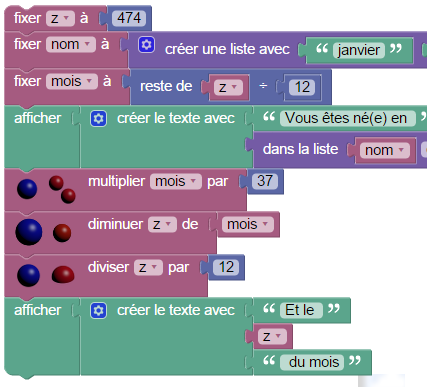
L’algorithme utilisé par le magicien est donné dans l’énoncé du bac, avec une variante. Basé sur le théorème de Bachet-Bézout, qui remonte à Bachet de Méziriac dont on reparlera plus bas, il se programme asez aisément.
Ceci dit, le sujet de bac ne demandait pas de soigner l’affichage, donc la version purement numérique, qui est évidemment bien plus simple, convient aussi :
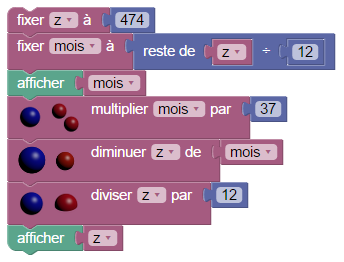
Arrondis
Une réserve naturelle contient initialement 531 441 oiseaux. Mais les ressources financières de celle-ci ayant été englouties dans l’achat d’un véhicule 4-4 pour son président, chaque année, le nombre d’oiseaux diminue du tiers chaque mois. Combien d’oiseaux restera-t-il au bout d’un an, soit 12 mois ?
Il s’agit de diminuer 12 fois de suite le nombre d’oiseaux, de son tiers :
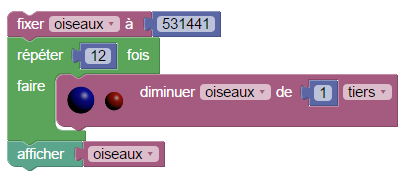
L’exécution de ce script révèle qu’il ne reste plus que 4 096 oiseaux au bout d’un an. Il faut une mesure d’urgence !
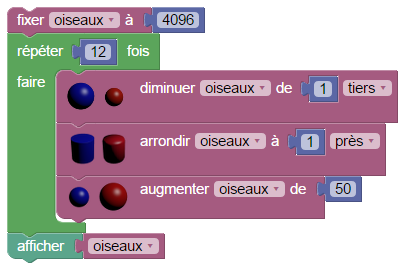
Constatant qu’il ne reste plus que 4 096 oiseaux, le successeur du président décide, par mesure d’urgence, de rajouter 50 oisillons par mois. Combien d’oiseaux restera-t-il au bout d’un an avec ce nouveau protocole ?
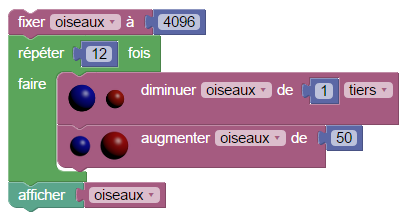
Comme c’est souvent le cas dans les sujets de bac sur les suites arithmético-géométriques, il y a un problème d’arrondis, le nombre d’oiseaux cessant vite d’être entier (ainsi que la limite de la suite). Ici par exemple il y a 0,413 oiseau de trop. Un modèle plus pertinent serait donc celui où on arrondit systématiquement le nombre calculé :
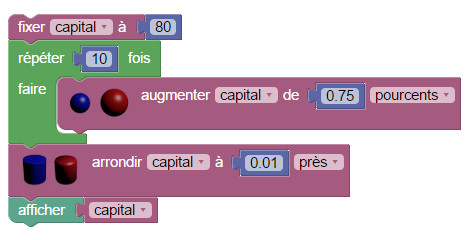
Un phénomène similaire se produit dans le monde de la finance, à ceci près qu’on arrondit au centième et plus seulement à l’entier. Par exemple, en plaçant 80 euros pendant 10 ans à 0,75 % d’intérêts composés, on aura au bout de 10 ans, 86,20 € :

On aurait pu préférer calculer le capital au bout de 10 ans par suite géométrique, et arrondir seulement après :
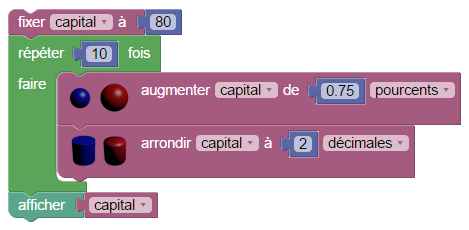
Et bien, on n’obtient pas le même résultat ; du moins avec certaines valeurs du capital initial et du pourcentage.
Remarque : On peut modifier l’arrondi grâce au menu déroulant qu’il contient ; les deux scripts suivants sont équivalents :

Listes de prix
Pour calculer le montant d’une facture en tenant compte de la TVA ou (ici) de promotions, voici un exemple possible :
Une remise de 10 pourcents est exceptionnellement accordée aujourd’hui.
Une remise de 20 pourcents est accordée sur tout achat d’une valeur supérieure à 320 €.
Voici un programme de calcul permettant de calculer une facture en tenant compte de cette remise. On considère l’achat de 3 articles coûtant 50 € chacun et 5 articles de valeur 40 € chacun.

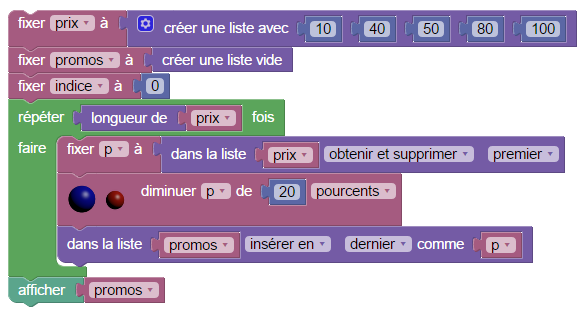
Maintenant, on peut avoir besoin de calculer les prix après réduction de 20 % pour plusieurs prix initiaux possibles ; par exemple pour des montants de 10€, 40€, 50€, 80€ et 100€. Pour cela, on constitue une liste de prix, et par bouclage, une liste initialement vide dans laquelle on va ajouter, l’un après l’autre, les prix après réduction, ce qui à la fin donnera une liste de tous les prix après réduction. Dans bloquement, les listes sont dans le menu Statistiques du menu Math.
Le problème est que la liste par défaut est une liste de 3 nombres, et là on en souhaite 5. On va donc faire appel à un « mutateur » de Blockly, qui est caché dans la petite roue dentée de « créer une liste ». En cliquant sur cette roue dentée, on voit apparaître un sous-menu contenant l’élément générique qu’on peut ajouter dans la liste, ainsi qu’un bloc dans lequel se trouvent trois éléments :
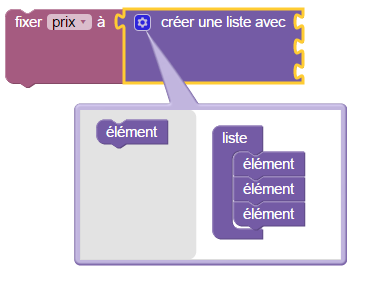
Il suffit maintenant de faire glisser deux fois l’élément générique de gauche vers le bloc de droite, et le tableau comprend 5 entrées. On y met 5 constantes valant respectivement 10, 40, 50, 80 et 100 pour avoir la liste des prix. Pour calculer la liste des prix après réduction, on boucle 5 fois (puisqu’il y a 5 prix) et à chaque répétition,
- on extrait le prix p de la liste des prix ;
- on le diminue de 20% ;
- on ajoute le prix réduit à la fin de la liste promos.
L’affichage final donne la liste des prix après réduction, séparés par des virgules :
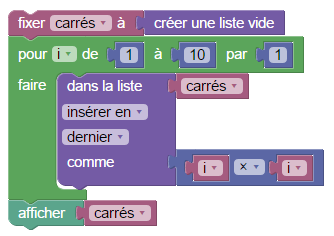
Pour créer la liste des carrés des entiers à un chiffre, on fait pareil mais avec une boucle « pour » (parce qu’on a besoin de l’indice i pour calculer son carré) :
Fibonacci
Le calcul de la suite de Fibonacci est facile dans un langage comme Python, grâce à l’affectation simultanée. Avec d’autres langages, il faut une variable supplémentaire permettant de mémoriser l’une des variables pour s’en servir lors de l’addition.
Par exemple, on va appliquer l’algorithme suivant, proche de la description de Fibonacci lui-même :
- fixer naissances à adultes parce que chaque adulte (en âge de procréer) donne une naissance ;
- augmenter adultes de juvéniles parce que les adultes restent adultes mais les juvéniles deviennent adultes ;
- fixer juvéniles à naissances parce que chaque lapereau devient juvénile (avant de devenir adulte au passage suivant dans la boucle).
Les termes successifs sont placés dans un tableau qui, au bout du compte, contiendra la suite de Fibonacci :

Le fichier avec ses commentaires peut être téléchargé pour le tester dans bloquement :
Cette technique permet de résoudre des problèmes d’évolution. Voici un exemple :
Un archipel de l’Océan Pas-si-fixe est constitué de deux atolls : L’atoll de Trikini, initialement peuplé de 3000 habitants, et l’atoll de Tetrakini, initialement peuplé de 4000 habitants. Chaque année, l’armée, en raison d’essais nucléaires, organise des déménagements, conduisant 25 % des habitants de Trikini à aller habiter sur Tetrakini, et simultanément, 30 % des habitants de Tetrakini allant habiter sur Trikini.
On demande quelle est l’évolution à long terme des populations des deux atolls.
Comme c’est par pirogue que les habitants vont d’une île à l’autre, on appellera pirogue1 et pirogue2 les variables servant à mémoriser les populations (ou plutôt les pourcentages) des deux îles, avant leurs réductions par émigration. Alors plutôt que réduire directement la population de 25 pourcents :
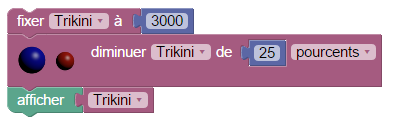
on va placer les 25% dans la pirogue puis soustraire le contenu de la pirogue, de la population insulaire (c’est une grosse pirogue) :

On a déjà la base du script complet, à part les problèmes d’arrondi :
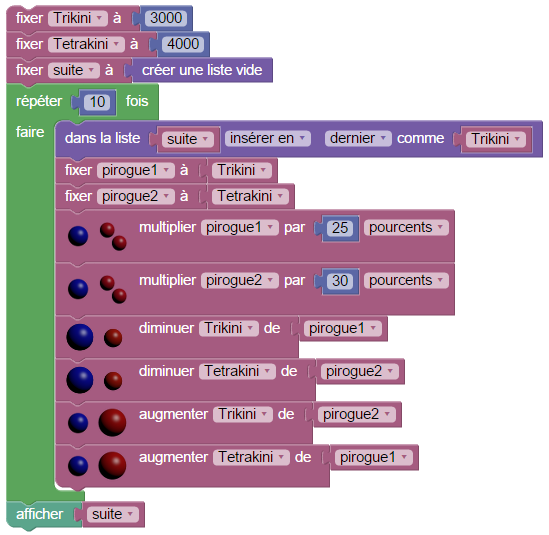
Avec les arrondis, on trouve des populations limites de 3818 habitants pour Trikini et 3182 pour Tetrakini.
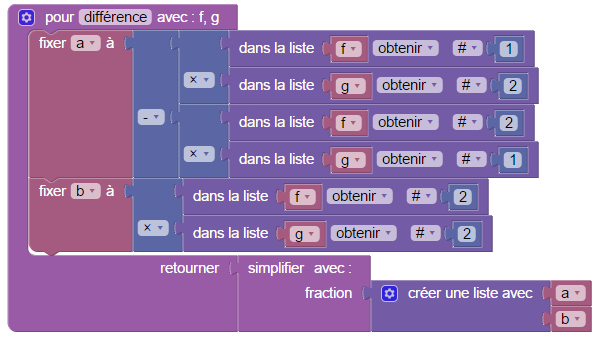
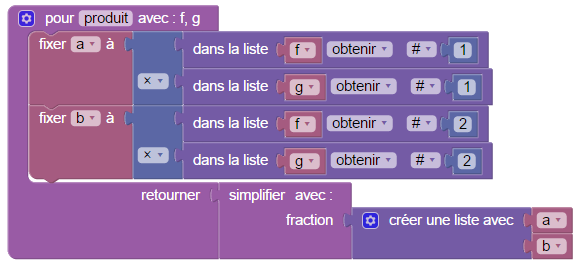
Fractions
Blockly gère les listes de nombres alors on se propose de représenter une fraction par une liste de deux entiers : Son numérateur et son dénominateur. Avant de voir comment on effectue les calculs sur les fractions, il faut donc définir une fonction d’affichage qui transforme par exemple la liste [3,2] en le texte 3/2. Et avant cela, il faut définir une fonction de simplification rendant les fractions irréductibles pour mieux les afficher. Pour simplifier au maximum une fraction, on divise son numérateur et son dénominateur par leur pgcd. Problème : Blockly n’a pas d’algorithme d’Euclide ni équivalent.
On démarre donc par la création d’une fonction pgcd de deux variables entières a et b. Autrement dit, on va construire un nouveau bloc et le rajouter à Blockly. Et pour éviter d’avoir à trop programmer en JavaScript, autant faire cela avec Blockly.
Dans le menu « Fabrique », on peut construire un bloc donnant une instruction (la première sorte) ou une fonction (la seconde sorte, on voit qu’il y a un « retourner » renvoyant une valeur). Là on voit un cadre où on donne son nom à la fonction (ici, « pgcd ») et un clic sur la roue dentée permet de gérer les entrées :
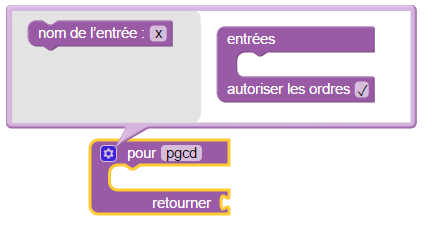
Par défaut la fonction n’a qu’un antécédent nommé x. On le renomme a puis on le fait glisser vers l’emplacement des entrées, et par miracle le x est toujours là, il était caché en-dessous du a. Alors on insiste, on le renomme b et on fait glisser ce b en-dessous de a :
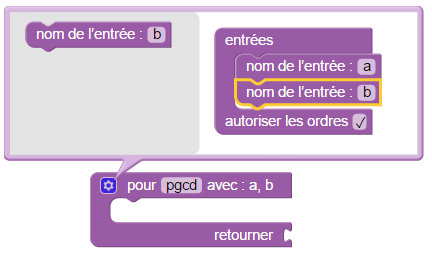
Ensuite il ne reste plus qu’à programmer l’algorithme d’Euclide dans le cadre définissant le pgcd (on constate qu’il a fallu une nouvelle variable r pour mémoriser le reste euclidien avant de modifier a et b) :
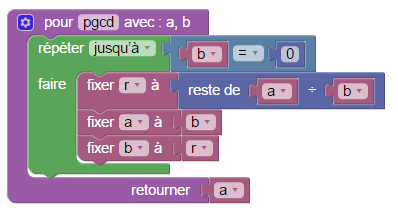
Après ça, il y a un nouveau bloc dans le menu « Fabrique », on s’en sert comme on se sert de tous les autres blocs :
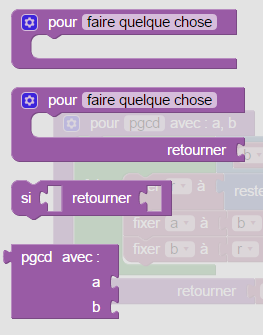
Par exemple pour afficher le pgcd de 24 et 36 :

On vérifie avec ce petit script, que 1/2+1/3=5/6 :
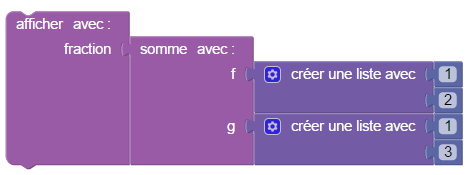
Voici le fichier Blockly permettant de calculer sur les fractions :
Dichotomie
Le célèbre jeu de la valise consiste à deviner un nombre entier, qui est le montant d’une cagnotte que l’on peut gagner simplement en l’annonçant à la radio. Mais l’animateur radio téléphone à une personne au hasard et cette personne ne peut gagner que si elle a été désignée par le hasard et qu’en plus elle a écouté la radio (c’est le but) pour connaître le montant de la cagnotte. On peut imaginer que peu de gens gagnent à ce jeu... Aussi, pour faire plus « social », certaines radios proposent une variante où, si la personne connaît le montant approximatif (par exemple, la personne a noté le montant la veille), on lui laisse une chance de deviner rapidement ce montant, en lui disant si sa proposition est plus grande (« c’est moins ») ou plus petite (« c’est plus ») que le montant réel. A priori ce genre de jeu favorise ceux qui ont le sens des ordres de grandeur. A posteriori ce genre de jeu favorise ceux qui connaissent la recherche par dichotomie et le pratiquer est une excellente occasion pour inventer l’algorithme de dichotomie.
Le montant de la cagnotte est un entier entre 1€ et 100€ inconnu. Chaque fois qu’on essaye de le deviner, la réponse dit si on a essayé trop bas, trop haut, ou juste. En combien d’essais maximum un candidat malchanceux peut-il deviner le montant ?
Pour programmer ce jeu, on commence par créer une variable (en réalité une constante puisqu’on n’y touchera plus) nombre, aléatoire entre 1 et 100. Comme il y a trois possibilités (le montant proposé est trop petit, trop grand ou pile poil), on utilise un test « si...sinon si...sinon » de Blockly. Chaque éventualité ne donne lieu qu’à un affichage, et les tests portent sur la comparaison entre le nombre proposé (appelé divination) et le nombre à deviner. Ces alternances test-affichage se font dans une boucle qui cesse lorsqu’on a deviné juste (égalité entre divination et nombre). Pour éviter que, par hasard, l’égalité soit vraie dès le début, on initialise divination à une valeur qui n’est pas dans l’intervalle du jeu. Et ensuite, cette variable est affectée au résultat d’une entrée de nombres (dans le menu « Entrées-sorties ») :

Ce jeu n’est pas très facile à programmer en classe mais pourrait faire l’objet d’un DM. Et surtout, c’est en y jouant qu’on exerce ses capacités au calcul mental et qu’on finit par inventer un algorithme dont on apprendra plus tard qu’il s’appelle dichotomie. Un exercice plus difficile (plutôt pour le prof mais permettant de faire de la pédagogie différenciée...) serait d’inverser les rôles, c’est-à-dire de programmer l’algorithme de dichotomie. On en arrive à quelque chose comme ça :
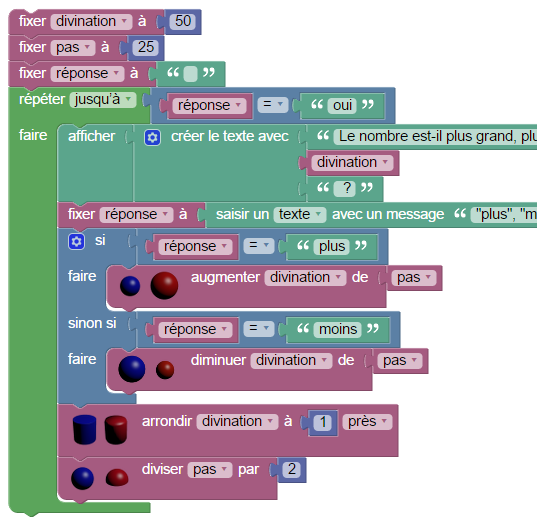
Pour répondre à la question de l’énoncé, on peut
- modifier l’algorithme précédent en y ajoutant un compteur, qui in fine, donnera le nombre de tentatives ;
- jouer avec l’algorithme non modifié et compter soi-même (calcul mental multitâche !) ;
- calculer directement le logarithme en base 2 de 100 (peut-être pas en collège...) ;
- Partir de la constatation que si à chaque étape, la largeur de l’intervalle contenant le nombre à deviner, est divisée par 2, et chercher à partir de quand cette largeur descend en-dessous de 1 :

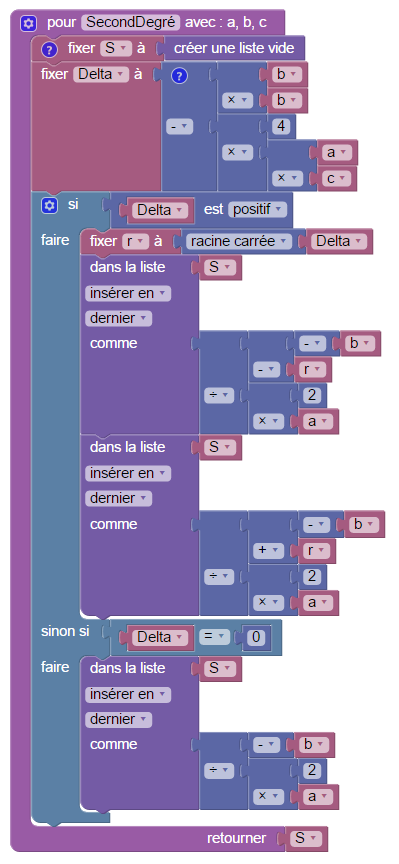
Cette activité sur un nombre à deviner peut mener au lycée, à la résolution d’une équation (ici, x²=3) par dichotomie (100% Blockly, il n’y a pas de Sophus là-dedans) :
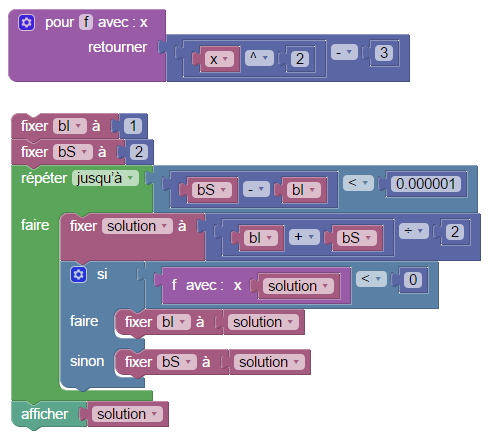
Ici on a programmé l’algorithme pour résoudre l’équation f(x)=0 où f(x)=x²-3, ce qui permet de le modifier pour résoudre d’autres équations du type f(x)=0, où f est croissante, en changeant simplement la définition de f et les bornes de l’intervalle.
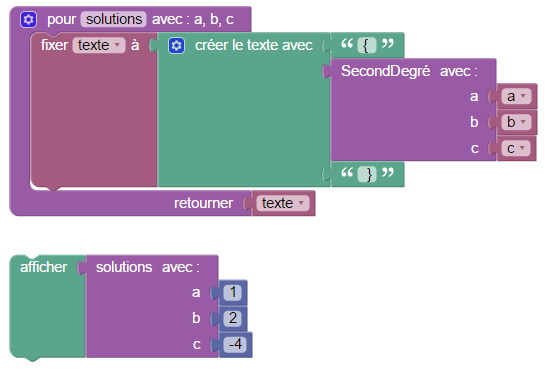
Bien entendu, si l’équation à résoudre est du second degré, on connaît un autre algorithme pour la résoudre.
Conjecture
On peut constater par calcul mental que
- 1+3 = 4
- 1+3+5 = 9
- 1+3+5+7 = 16
etc.
On peut aussi émettre la conjecture après avoir fait calculer la somme par Blockly.
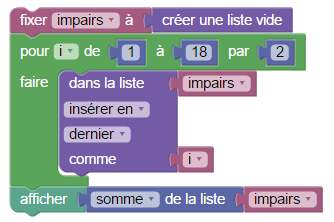
Pour additionner des nombres, on crée une variable somme que l’on augmente de 1 puis de 3 puis de 5 etc. Les incréments seront donc eux-mêmes des variables et varieront eux-mêmes par incréments de 2. On calcule donc la somme des entiers impairs en deux lignes de Sophus :
augmenter somme de incrément
augmenter incrément de 2Il suffit de faire ça 10 fois pour avoir la somme des 10 premiers nombres impairs. Mais tant qu’on boucle, on peut ajouter dans une liste, les valeurs successives des sommes partielles, ce qui donne d’un coup plusieurs sommes de carrés (ci-dessus on peut voir que pour calculer 1+3+5 on peut faire 4+5 et éviter de faire plusieurs fois le même calcul) :
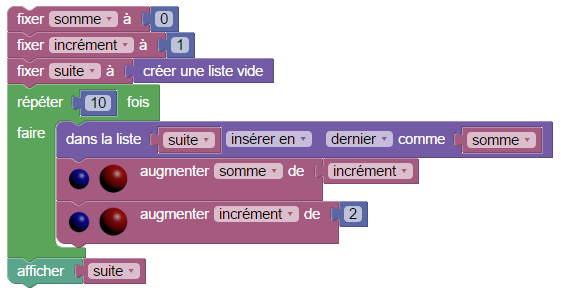
Une fois la conjecture émise, on peut (on a le droit !) ressentir l’envie de la prouver. Au collège, on pense évidemment au calcul n²+2n+1=(n+1)² (si on sait que le n-ème entier impair est 2n+1) qui est d’ailleurs l’ébauche d’une démonstration par récurrence ; mais peut-être prépéfera-t-on la preuve sans mot suivante :

Analyse
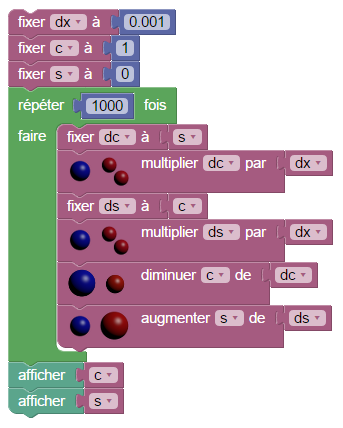
La théorie des groupes de Lie fait partie de l’analyse, il ne faut donc pas s’étonner que Sophus soit un langage de programmation particulièrement adapté au calcul différentiel et intégral.
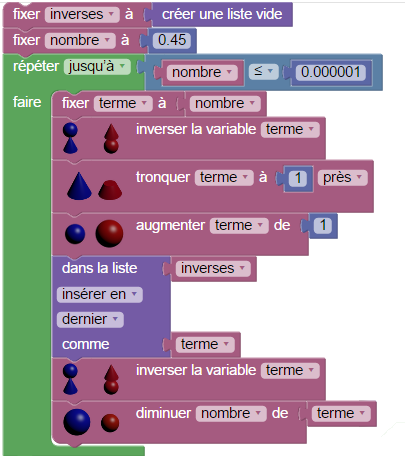
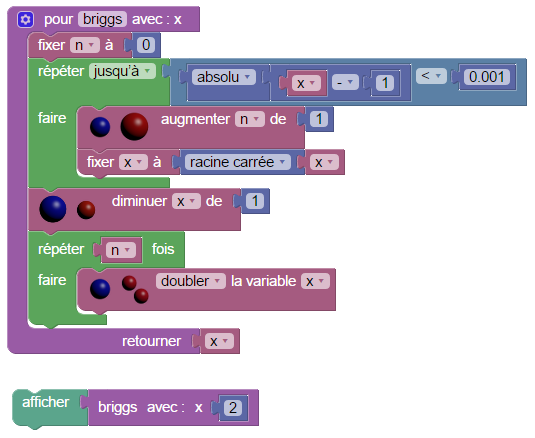
Algorithme de Heron
Pour calculer √3 à 0,000001 près il suffit de trouver une suite qui converge vers √3 et de calculer un terme de cette suite de rang suffisamment élevé pour que la limite soit atteinte à 0,000001 près. L’algorithme de Heron d’Alexandrie consiste à répétitivement calculer la moyenne entre x et 3/x où x est une valeur approché de √3.
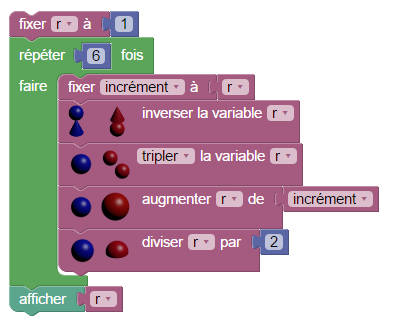
En fait il suffit de boucler 6 fois pour atteindre le maximum de précision permis par la machine :
Intégrale
L’intégrale de f se dit « somme de f(x)dx » et il suffit donc d’additionner des termes de la forme f(x)dx pour obtenir une valeur approchée de l’intégrale. L’addition se fait à partir de x=a jusqu’à ce que x dépasse b :

Voici des programmes de calcul de Bachet de Méziriac, et autres algorithmes historiques :
Problème VIII
Un beau problème de Bachet de Méziriac, « style Rallye » :

La traduction « moderne » peut être celle-ci :
Quelles doivent être les valeurs initiales des variables premier, second et troisième pour qu’à la fin du script ci-dessous elles vaillent toutes 8 ?

Pour chercher la solution par tâtonnements (ce que ne faisait pas Bachet), on peut charger dans bloquement le fichier suivant, où l’énoncé a été recopié sous forme de commentaires (on lit un commentaire en cliquant sur les roues dentées des instructions) :
Problème IV

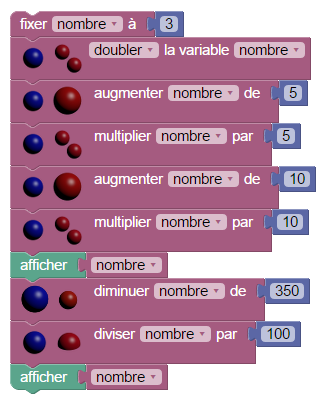
Dans le script ci-dessous, le premier affichage est le nombre annoncé par le spectateur, et le deuxième affichage est le nombre donné par le magicien, qui se trouve correspondre au nombre deviné (sauf si le spectateur a mal calculé).
Problème I
Le premier des problèmes de Bachet n’est pas le plus simple puisqu’il y a un test de parité :

Puisqu’il y a parfois un terme correctif à additionner dans le calcul, on peut additionner ce terme de toute manière mais le rendre nul s’il n’était pas additionné (en effet additionner 0 ne modifie pas un nombre) :

Nim
Le jeu de Nim dit « de la soustraction » était déjà connu de Bachet de Méziriac, à ceci près qu’on additionnait jusqu’à atteindre ou dépasser une somme, plutôt que soustraire jusqu’à atteindre 0 :

Le problème XXII a été traduit en français moderne.
Ce jeu fait en quelque sorte appel à un mini-langage de programmation, comprenant les incrémentations de 1, 2 ou 3 (soit 3 instructions à la Sophus) et que l’on peut donc assez facilement programmer en Blockly.
Le résultat est téléchargeable ci-dessous, c’est un dossier à décompresser pour y trouver un fichier « poursuite.html » sur lequel il suffit de double-cliquer pour jouer à ce jeu :
Le jeu est intéressant aussi à programmer avec la tortue : Chaque joueur choisit entre
- avancer de 10 pixels ;
- avancer de 20 pixels ;
- avancer de 30 pixels ;
et le premier joueur qui parvient à mener la tortue à la frontière située à 210 pixels, gagne. La version Scratch peut être visionnée ici. Et voici une version 100% JavaScript puisque ce langage, avec les boutons, est très adapté à la programmation évènementielle :
Il s’agit là aussi de la version à deux joueurs humains, l’ordinateur ne servant que comme plateau de jeu (une sorte de micromonde).
Seaux
Encore un problème célèbre de Bachet de Méziriac :

Avec une version plus modernement orthographiée :
| Deux bons compagnons ont 8 pintes de vin à partager entre eux également, lesquelles sont dans un vase contenant justement 8 pintes, et pour faire leur partage ils n’ont que deux autres vases dont l’un contient 5 pintes, et l’autre 3. On demande comment ils pourront partager justement leur vin, ne se servant que de ces trois vases. |
On peut faire de cet exercice un exercice d’algorithmique basé sur un langage de programmation réduit, ne comportant que 3 instructions :
- vider un seau (dans la citerne, le tonneau ou la rivière) ;
- remplir un seau (à ras-bord) ;
- transférer autant d’eau que possible d’un seau dans l’autre (jusqu’à ce que le premier seau soit vide, ou le second, plein).
Voici une proposition, où le vin a été changé en eau, et où a été ajoutée une quatrième instruction (affichage) et où les déclarations de variables sont insérées d’office dans le script. Au passage on a remplacé les données 5 et 3 par 8 et 5 pour corser un peu le problème. Le résultat peut être téléchargé ci-dessous et utilisé hors ligne :
La mission a aussi été changée, pour que la quantité à fournir ne soit pas forcément 1 litre, mais tout nombre entre 1 et 7 litres, obtenu au hasard.
Voici une solution possible avec cet outil :

Fermat
Fermat coyait que les nombres qu’il a inventés étaient premiers, selon le raisonnement inductif que voici :
- 2 élevé à la puissance 1 (qui est la plus petite puissance de 2), donne 2 ; en ajoutant 1 on a 3 qui est pemier ;
- 2 élevé à la puissance 2 vaut 4, et en ajoutant 1 on obtient 5 qui est aussi premier ;
- 2 élevé à la puissance 4 donne 16 et 17 aussi est premier...
D’où cette magnifique description du raisonnement inductif :
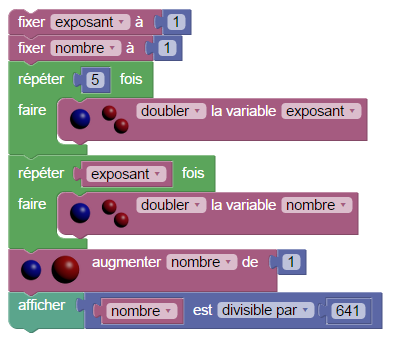
On sait depuis Euler que Fermat s’est trompé (et un juge qui fait une erreur d’induction, c’est un peu effrayant !). En fait le cinquième nombre qu’il propose n’est déjà pas premier. Pour le calculer, on va utiliser un programme de calcul :
- la variable exposant initialisée à 1, est doublée 5 fois de suite, ce qui donne 32 pour sa valeur finale.
- ensuite on double la variable nombre 32 fois, ce qui fait que puisqu’elle aussi était initialisée à 1, elle vaut 232 à la fin ;
- on l’augmente de 1 pour avoir le 5-ème nombre de Fermat
Et si on demande s’il est premier, l’affichage dit false ce qui veut dire qu’il est composé :

Pour en savoir plus, voyons ce qu’en dit Euler : Un de ses nombreux théorèmes dit que si un nombre de Fermat (d’indice n) n’est pas premier, il ne peut avoir pour diviseur qu’un nombre congru à 1 modulo 2n+1. Ici il s’agit des multiples de 64 plus un, et Euler propose alors de les chercher de cette manière :
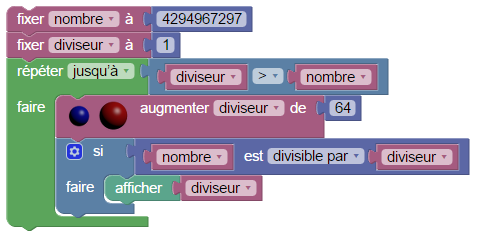
On découvre assez vite que 641 est un diviseur :
Calcul de π
Voici deux algorithmes de calcul de π :
Viète
Viète donnait plutôt une formule qu’un programme de calcul :

Sa traduction en Sophus est plutôt courte :

Euler
L’algorithme d’Euler est plus compliqué mais plus connu :

Voici sa traduction en Sophus :

Méré
Le chevalier de Méré était un grand amateur de jeux de hasard, et a constaté que si on lance 4 fois un dé, la probabilité d’avoir au moins une fois 6 dépasse légèrement 0,5 alors que si on lance 24 fois un dé, la probabilité d’avoir au moins une fois un double 6 (« sonnez ») est légèrement inférieure à 0,5. Voici ce que Blaise Pascal pensait de ce que le chevalier Méré pensait de ce phénomène :

Pour étudier le premier problème (probabilité d’avoir un 6 en lançant 4 fois le dé), on va gagner un peu de temps si on lance 4 dés en même temps. On va modéliser le gobelet contenant ces 4 dés sous forme d’une liste ; et pour savoir si le 6 est tombé, on va regarder quand il est tombé pour la première fois :

Si le 6 n’est jamais tombé, l’affichage est 0 ; on reconnaît donc la présence d’un 6 dans la liste gobelet, au fait que ce nombre est strictement supérieur à 0 ; si c’est le cas, on incrémente le compteur, qui à la fin, contiendra alors le nombre de lancers de gobelet victorieux :
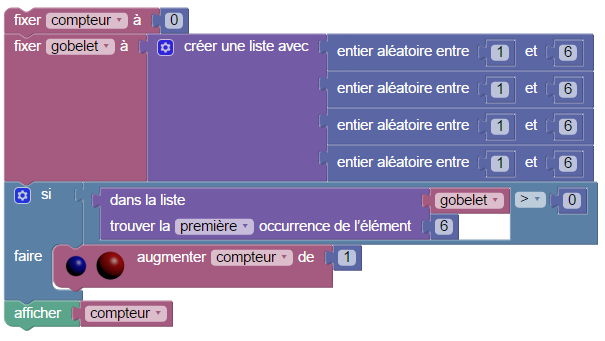
Il suffit de placer tout ça dans une boucle pour avoir une estimation de la probabilité (l’estimation, c’est la fréquence de parties victorieuses) :
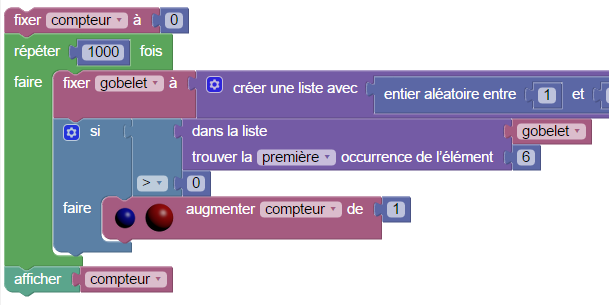
C’est probablement en faisant ça mais de façon moins virtuelle, que le Chevalier a constaté le phénomène dans des tavernes aventureuses. Mais revenons à ce qu’en a pensé l’auteur des pensées : Pour calculer la valeur exacte de la probabilité, on divise le nombre de cas favorables par le nombre de cas possibles. On calcule ces nombres dans des boucles imbriquées, le compteur casPossibles étant systématiquement incrémenté, le compteur casFavorables n’étant incrémenté que s’il y a un 6 parmi les indices des boucles :
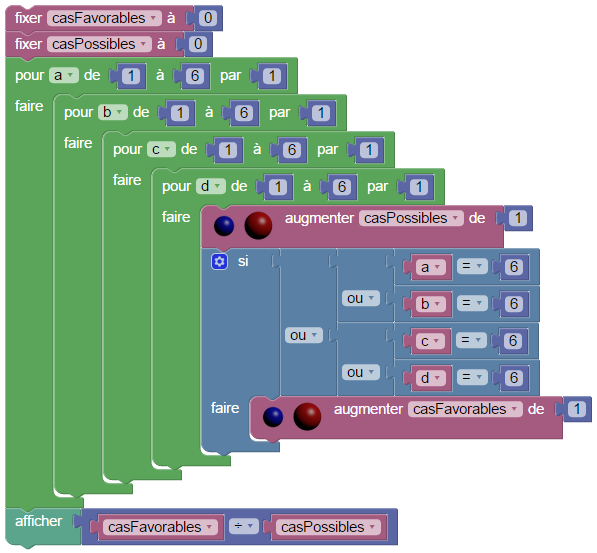
La probabilité est effectivment supérieure à 0,5.
On peut aller plus loin en cherchant à partir de combien de lancers de dé, la probabilité d’avoir un 6 dépasse 0,5 ; ou plutôt à partir de combien de lancers, la probabilité de perdre descend en-dessous de 0,5 :

Pourquoi plus loin ? Parce que
- on peut explorer d’autres seuils que 0,5 (et découvrir la loi géométrique) ;
- on peut aussi avec cette technique aborder le second problème du chevalier de Méré, puisque si on lance deux dé, la probabilité d’avoir un double 6 (« sonnez ») est 1/36 donc la probabilité de ne pas en avoir un est 35/36, et on trouve qu’il faut lancer le double dé 25 fois pour dépasser la probabilité 0,5 :
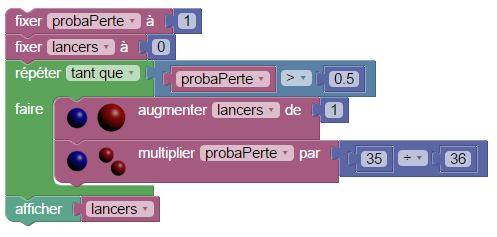
Les simulations probabilistes sont très diverses avec les modèles qu’on peut élaborer et tester en programmation graphique (voir l’exemple Logo ci-dessus). En voici quelques exemples qui peuvent aller jusqu’au post-bac :
Poker d’as
Le jeu de poker d’as est intéressant parce qu’il y a une stratégie à chercher : Si on a un brelan (3 dés identiques) on a intérêt à ne relancer que les deux dés restants pour essayer d’avoir un carré (4 dés identiques), un poker (5 dés identiques) ou au moins un full (brelan+paire). C’est donc une excellente occasion pour pratiquer les tests (ou instructions conditionnelles).
Et avec la possibilité qu’offre Blockly d’extraire un élément au hasard dans une liste, il suffit de faire une liste des faces du dé pour avoir un dé spécial de poker d’as. La présence, dans Unicode, de caractères représentant les pièces du jeu d’échecs, a incité à choisir
- le trèfle ♣ pour représenter l’as ;
- le fou ♝ pour représenter le valet ;
- la dame du jeu d’échecs ♛ pour remplacer celle du jeu de cartes ;
- le roi ♚ pour ... le roi !
- et les 9 et 10 sont des nombres
On peut alors simuler le lancer des 5 dés par cet algorithme :
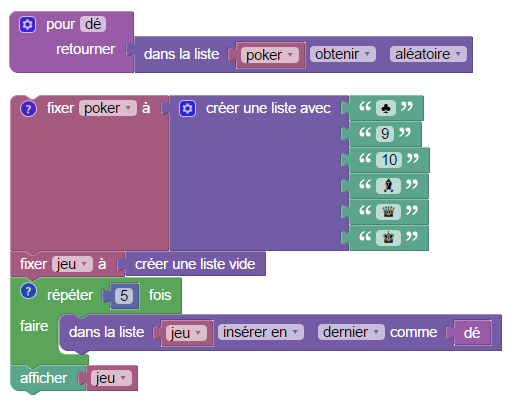
La liste jeu contient les 5 résultats des lancers, on les insère au fur et à mesure dans la liste. Et la liste poker contient les 6 faces d’un dé, en choisir une au hasard (lancer le dé...) se fait dans une procédure ad hoc.
On peut essayer le fichier dans bloquement, après l’avoir téléchargé ici :
Stats
Pour faire un tableau d’effectifs, on crée le tableau avec des effectifs initialemant nuls. Ensuite chaque fois que le dé (par exemple) tombre sur 3, on incrémente l’effectif correspondant à 3. On peut le faire comme ça :
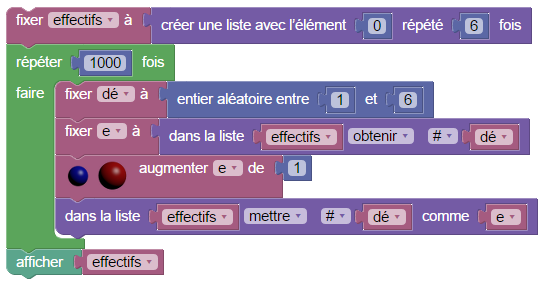
Mais pour obtenir des indicateurs statistiques, on peut simplement mettre les résultats du lancer de dé dans une liste et invoquer le menu « statistiques » du menu « Maths » :

Qui dit statistiques, dit diagrammes statistiques. Le fait que GeoTortue permette de gérer plusieurs tortues en même temps, a permis à Julien Pavageau de faire des diagrammes en bâtons dans l’onglet « courses de tortues » de cet article.
Condorcet
En appliquant la technique vue dans l’onglet sur le poker d’as, on peut aussi simuler des dés non transitifs.
Albert, Béatrice et Charlotte possèdent chacun son propre dé parfaitement équilibré ; mais le dé d’Albert porte les nombres 1, 6, 11, 12, 13, 14 alors que le dé de Béatrice porte les nombres 2, 3, 4, 15, 16, 17 et celui de Charlotte porte les nombres 5, 7, 8, 9, 10, 18. Albert joue contre Béatrice : Ils lancent chacun son dé et celui ou celle qui a le plus grand numéro gagne. Vérifier par simulation que Béatrice gagne en moyenne contre Albert, Charlotte contre Béatrice et Albert contre Charlotte.
Pour simuler 1000 matchs entre Albert et Béatrice :
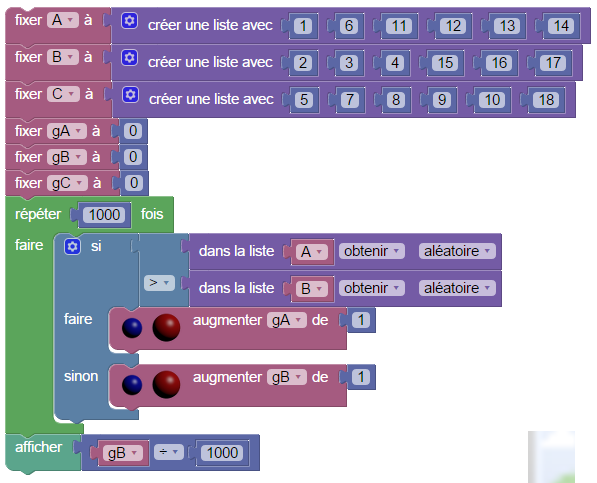
Urnes
On peut découvrir expérimentalement la théorie de l’échantillonnage, en constituant une urne et en effectuant des tirages (avec ou sans remise) dans cette urne.
Dans une entreprise de 100 employés, un vote a été organisé sur le thème « êtes-vous pour ou contre les élections ? ». L’urne est déposée devant la machine à café et le comité d’entreprise essaye de savoir avant le dépouillement quelle tendance émerge. Pour cela, un de ses membres secoue discrètement l’urne de façon à faire glisser un des bulletins de vote et regarde ce qu’il dit. Puis, tout aussi discrètement, il remet en place le bulletin et repose l’urne.
Deviner une tendance à partir d’un seul bulletin, ce n’est guère raisonnable, mais on va voir qu’il est facile de constituer un échantillon de taille 64 (sur un total de 100, ça non plus n’est guère raisonnable). Pour construire l’urne, on la crée comme une liste vide puis on la bourre en mettant successivement des « pour » puis des « contre » :

Le tricheur effectue un tirage de 64 bulletins avec remise. On ajoute donc une boucle dans lequelle on tire un bulletin au hasard, et si ce bulletin porte « pour », on incrémente la variable espoirs qui, du coup, contiendra le nombre de « pour » (dans l’échantillon) à la fin. Le résultat du sondage est affiché à la fin :
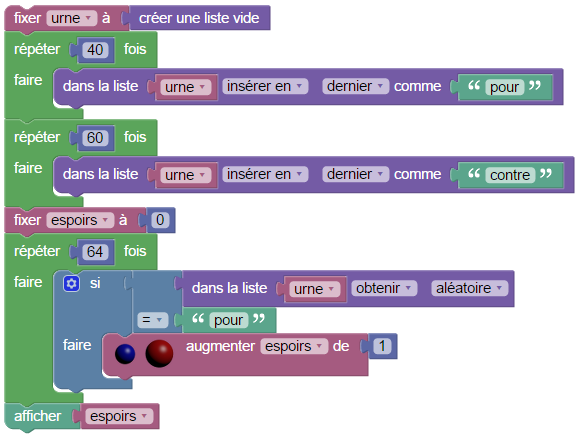
Tirages sans remise : Il est très facile de rendre l’exercice un peu moins délirant, en remplaçant « obtenir » dans le script ci-dessus, par « obtenir et supprimer » : Le tirage obtenu est alors sans remise, et bien plus conforme à des situations réelles (jeux de cartes, loto, sondages d’opinion, sondages de sortie d’urnes etc.).
Lois classiques
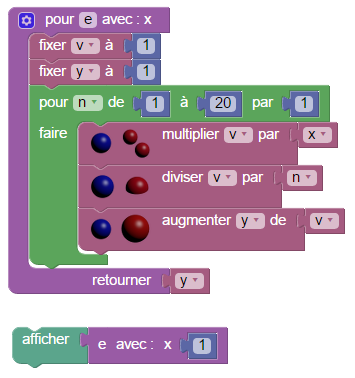
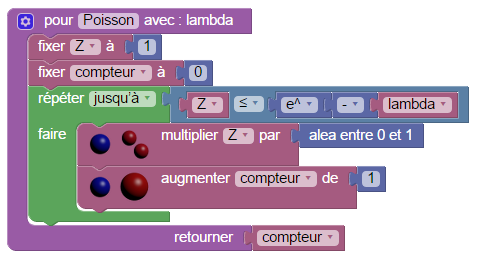
Le bloc « aléa entre 0 et 1 » simule une variable aléatoire uniforme entre 0 et 1. On peut s’en servir pour simuler une variable aléatoire exponentielle de paramètre λ avec cet algorithme, placé dans une fonction. Dans le menu « Fabrique » on choisit le second bloc « pour faire quelque chose...retourner » puisqu’il y aura la variable aléatoire à retourner. On renomme le bloc en VAexpo (abréviation pour « variable aléatoire exponentielle ») et on programme ceci :

Dès lors, on dispose dans le menu « Fabrique » d’un nouveau bloc :

ceci permet alors de s’en servir pour simuler une variable alatoire de Poisson (paramètre : le même λ), avec la situation suivante :
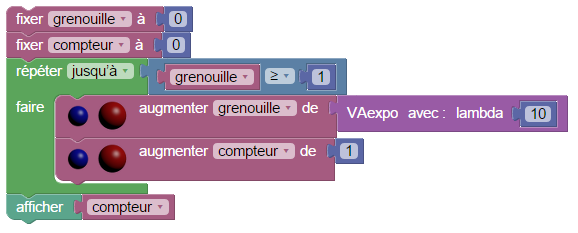
Une grenouille effectue des sauts exponentiels de paramètre 10. En combien de sauts aura-t-elle parcouru au moins un mètre ?
Le nombre de sauts suit une loi exponentielle de paramètre 10.
Voici la version Scratch :

Et la version Sophus :
Loi normale
On peut simuler une variable aléatoire normale centrée réduite en faisant effectuer à la grenouille 12 sauts uniformes à partir de l’abscisse -6 :

En appliquant à une telle variable aléatoire une fonction affine, on peut obtenir ,’importe quelle autre variable aléatoire normale.
Anniversaires
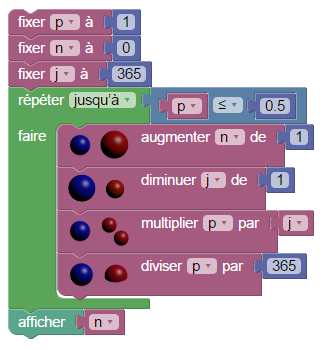
Quel est l’effectif minimal d’un groupe tel que dans ce groupe, la probabilité que deux personnes aient leur anniversaire le même jour, dépasse 0,5 ?
On calcule ce nombre par une boucle ;
- p est la probabilité que parmi n personnes, aucune n’ait son anniversaire le même jour qu’une autre ;
- n est le nombre de personnes de l’assemblée ;
- j est le nombre de cas favorables (nombre de jours où il n’y a pas encore d’anniversaire)
Jeux combinatoires
La possibilité qu’offre Blockly de fabriquer ses propres blocs permet de faire des jeux en Blockly. Un exemple est la bataille navale traduite du tableur vers Blockly. Le résultat est ici, et fait appel à des blocs créés ad hoc [2] : On peut imaginer un Blockly par activité. Voici quelques exemples de Blockly « tunés » pour des activités spécifiques, choisies comme des jeux combinatoires dans le champ numérique (comme ça on peut les commencer en calcul mental, ça ne fait pas de mal) :
Monde
Un jeu du Monde consistait à chercher un nombre dont un certain programme de calcul inversait l’ordre des chiffres. Sa traduction sophusienne devient celle-ci :
Un bug a malenconteusement flouté la valeur de départ du nombre. Mais juste avant de faire sa copie d’écran, le hacker avait constaté que l’affichage final donnait le même nombre mais avec l’ordre des chiffres inversé. Quel est ce nombre ?

Collatz
La suite de Collatz est un grand classique de l’algorithmique. En Sophus elle se programme ainsi :
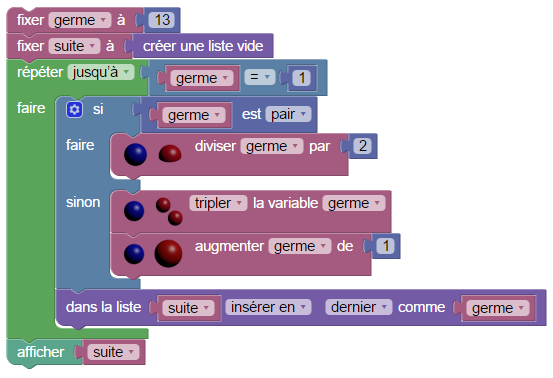
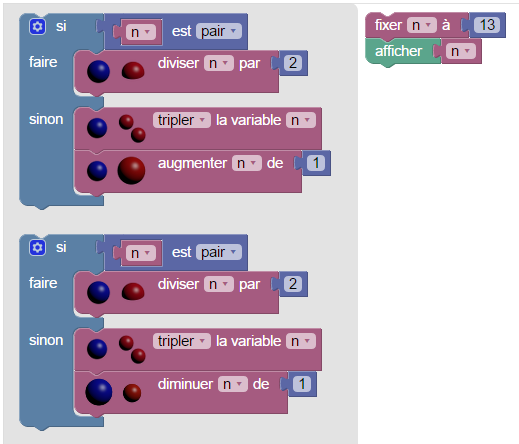
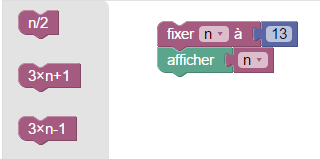
Un dénommé John Isbell a inventé un jeu basé sur la suite de Collatz : beanstalk ou « Jack and the Giant » (le jeu fait référence à la légende du haricot géant, où le géant propose un jeu à Jack ; beanstalk veut dire gousse de haricot). Chaque joueur à son tour fait une opération de la suite de Collatz (diviser le nombre par 2 s’il est pair, le tripler puis incrémenter le résultat sinon). Le premier arrivé à 1 a gagné. Pour en faire un vrai jeu, Isbell propose les ajouts suivants :
- Le premier joueur choisit le nombre entier qu’il veut, mais strictement supérieur à 1 (sinon il jouerait 1 et gagnerait sans même jouer) ;
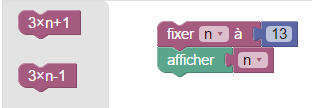
- Si le nombre est impair, on a le choix entre 3x+1 et 3x-1.
Les images ci-dessous sont cliquables, on peut, en cliquant dessus, télécharger la version de Blockly qu’elles illustrent.
Le jeu est intéressant à explorer en calcul mental, et des stratégies gagnantes émergent assez vite. Voici des approches utilisant Blockly :
D’abord, avec Sophus, on peut garder tout Sophus et ne laisser dans le menu, que les deux possibilités :
Chaque tour de jeu consiste à glisser un des deux blocs Sophus juste au-dessus de l’affichage.
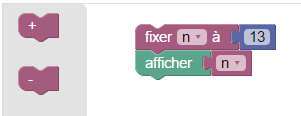
Plus simple, on peut créer ses propres blocs, ayant le même effet :
On peut même avec les mêmes blocs, simplifier la présentation :
Et si les joueurs ont compris le principe de la parité et n’essayent pas de tricher, on peut programmer directement la suite de Collatz :
Une autre amélioration de ce jeu a été proposée par Hohn Horton Conway : Une fois qu’on a calculé 3n+1 ou 3n-1, on divise automatiquement par 2 et ce, jusqu’à ce que le résultat soit à nouveau impair. Comme les stratégies gagnantes ne sont pas les mêmes que pour beanstalk, Conway a baptisé beans don’t talk cette variante :
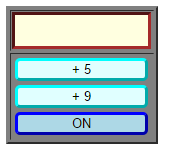
Et pour comparaison, le même jeu, programmé directement en JavaScript :
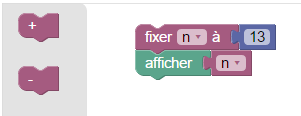
Le fichier est simpliste (en particulier, il faut un peu de calcul mental pour vérifier/anticiper les résultats affichés), et on joue non contre la machine, mais contre un autre joueur humain dans le style « clavier à 4 mains ». Pour démarrer un jeu, cliquer sur le bouton
à droite. Ensuite, un texte rappelle à qui c’est le tour de jouer, le joueur démarrant la partie s’appelant par convention « Jack », et l’autre joueur (affiché en rouge) s’appelant « Géant ».
Pour jouer, Jack clique, soit sur « + », soit sur « - ». Normalement, le nombre devrait alors changer selon la règle du jeu, et l’affichage précise que c’est au tour de Géant de jouer. Ce qu’il fait alors aussi en un seul clic. Etc.
Lorsqu’on est arrivé à 1, la partie est finie. En effet :
- si on joue
: 1 est triplé et donne 3, puis on ajoute 1 et on a 4, que l’on divise par 2 deux fois de suite : On retrouve1 ;
- si on joue
: 1 donne 3 par triplement mais ensuite on soustrait 1, ce qui donne 2. Mais là aussi, en divisant par 2, on retombe sur 1.
Par consèquent, si on essaye quand même de jouer, l’affichage numérique donne « undefined » et on doit cliquer sur
pour démarer une nouvelle partie. Par contre, avant ce geste, on a l’historique de la partie en bas de page, sous forme d’une suite de « + » et de « - ».
Score
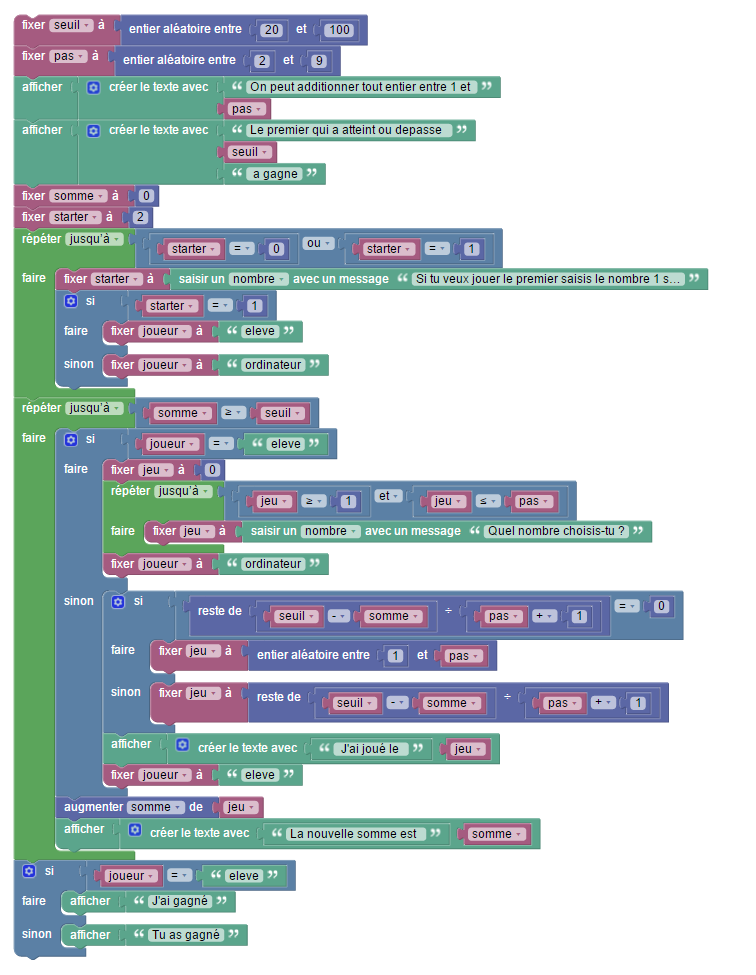
Un autre jeu mathématique du Monde consistait à deviner le nombre d’actions permettant de totaliser un score de 32 points, avec ces règles :
Le sport « handfootball » a ceci de particulier qu’on peut y marquer un but, au choix avec le pied comme au football, ou à la main comme au handball. L’arbitre accorde 5 points pour chaque équipe marquant un but au pied, et 9 points pour chaque équipe marquant un but à la main. La redoutable équipe des « All Blues » menée par « Kilomètres Davis » a déjà totalisé 32 points à la première mi-temps. Combien de buts de chaque sorte a-t-elle marqués ?
Il s’agit d’arriver à 32 en ajoutant à chaque fois, ou bien 5, ou bien 9. C’est donc comme un jeu de Nim simplifié (et à un seul joueur). Pour le fabriquer avec Blockly, on va créer deux blocs, de types respectifs « plus5 » et « plus9 ». Le premier se définit ainsi :
Blockly.Blocks['plus5'] = {
init: function() {
this.appendDummyInput()
.appendField("+ 5");
this.setPreviousStatement(true);
this.setNextStatement(true);
this.setColour(330);
this.setTooltip('but au pied');
this.setHelpUrl('');
}
};On voit qu’on a ajouté à Blockly.Blocks (la collection des blocs originaux de Blockly), un nouveau bloc de nom « plus5 » et dont la fonction d’initialisation (le pedigree en quelque sorte) consiste à ajouter à sa propre définition
- une entrée factice (parce que le texte ne peut être ajouté qu’aux entrées et pas directement) ; à laquelle est ajouté le texte « + 5 » qui se verra dans l’aspect extérieur du bloc ;
- un branchement possible vers le bloc qui est au-dessus ;
- un branchement possible vers le bloc qui est en-dessous ;
- une couleur numéro 330 (lie de vin) ;
- un texte d’aide ;
- un lien vers l’article wikipedia concernant l’ajout de 5 (vide lui aussi, l’article n’existant pas encore).
Ce script, engendré automatiquement par l’utilitaire en ligne, est placé avec son équivalent pour les buts à la main, dans un fichier JavaScript séparé de celui de Blockly et appelé blocks_complements.js. Ce fichier est chargé par la page html, ainsi que celui de Blockly. Ceci définit l’asepect des blocs ; pour qu’ils fonctionnent il faut aussi définir leur comportement, sous le fomre du JavaScript engendré chaque fois qu’on en place un sur la feuille de travail. Ce qui se fait dans un autre fichier appelé javascript_complement.js (on aurait pu choisir Python aussi), et contenant ceci :
Blockly.JavaScript['plus5'] = function(block) {
return 'n = n + 5;\n';
};Plus quelque chose d’analogue pour « plus9 ». Ensuite, pour avoir une boîte à outils permettant d’ajouter 5 ou 9, on met ces blocs dans le xml définissant la boîte à outil (menus avec sous-menus etc). Ici :
<xml id="toolbox" style="display: none">
<block type="plus5"></block>
<block type="plus9"></block>
</xml>Le résultat peut être téléchargé ci-dessous, en cliquant sur la copie d’écran :
Ce jeu peut être présenté sous d’autres formes, par exemple avec la tortue, qui, en avançant de 50 pixels ou de 90 pixels à la fois, doit parcourir exactement une distance totale de 320 pixels. Ou la version « calculatrice cassée », téléchargeable ci-dessous :
Diviseurs
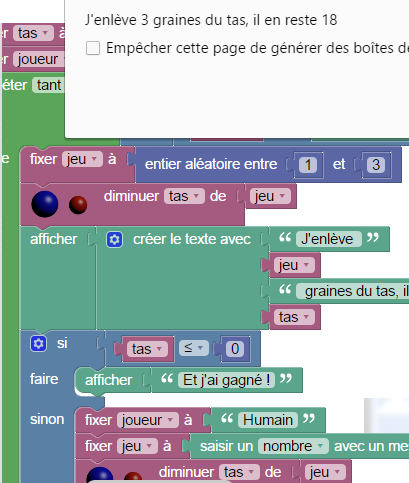
Un autre jeu mathématique du monde, une variante du jeu de Nim version « soustraction » :
Le premier joueur (ou l’arbitre) choisit un nombre entier supérieur à 1 ; chacun son tour lui soustrait un diviseur propre ; le premier qui arrive à 1 a gagné.
Par exemple, les diviseurs propres de 12 sont 1, 2, 3, 4, et 6 (pas 12 lui-même sinon c’est tricher).
On peut programmer ce jeu, en définissant un nouveau bloc de bloquement, appelé jouer ; il sera associé au nombre d qu’on veut jouer :
- si n est divisible par d et inférieur à d, on soustrait d à n et on affiche la nouvelle valeur de n ;
- sinon on affiche un texte d’erreur disant que d n’est pas un diviseur propre de n.
Voici le script en Sophus :

Ensuite, le bloc « jouer avec » peut être utilisé dans Blockly, mais d’une part il s’affiche par défaut en « entrées externes », d’autre part il lui manque le nombre qu’on veut jouer. On va donc en placer un dans l’espace de jeu travail, qui sera affiché en ligne et associé à un diviseur. Après avoir réduit la définition du bloc, le jeu peut être commencé :
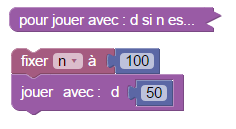
Le fichier ci-dessous peut être ouvert dans bloquement pour jouer :
Pour jouer,
- au début, choisir le nombre de départ (à la place de 100), et le diviseur à jouer en premier (à la place de 50) ;
- chacun son tour, les joueurs dupliquent le dernier bloc et modifient le champ du diviseur, puis clique sur le bouton en bas à gauche.
- Quand l’affichage final donne 1, le jeu se finit par la victoire de celui qui vient de jouer, car 1 n’ a pas de diviseur propre et on ne peut donc plus jouer.
Voici un exemple de partie, où celui qui joue en premier a perdu (alors qu’il aurait pu gagner) :

Et la version 100% JavaScript, sous forme d’un fichier html à tester ou télécharger (par exemple pour l’étudier) :
Enfin, les heureux possesseurs d’une machine sous Android pourront installer ce fichier apk pour jouer à ce jeu sur leur smartphone (mais en dehors des cours, hein !) :

Il s’agit d’un habillage (deux joueurs s’affrontent sur une seule tablette) provenant de cet article.
Ne pas oublier aussi le jeu de Nim présenté dans la partie sur Bachet de Méziriac.
Post-scriptum
Voici une fiche d’AP menée en 4e par deux professeurs de mathématiques :
Les élèves avaient déjà pratiqué Scratch mais seulement dans le domaine graphique. Le thème de cette activité étant le calcul formel, Sofus a été choisi pour raccourcir la construction des programmes de calcul et ainsi libérer les élèves du temps de programmation pour leur permettre de passer plus de temps sur le calcul formel. Les compétences visées étaient :
- C3 : Calculer en utilisant le langage algébrique
- Créer des applications simples
- Pratiquer des langages
Se sont révélés intéressants, à l’usage :
- le changement de syntaxe (par rapport à Scratch)
- la modélisation que permet Sofus (utilisation des deux variables presque plus comme des variables mathématiques que comme des cases mémoires).
- l’enchaînement avec la spirale (à ne pas confondre avec l’enseignement spiralaire)
La séance a été menée en classe entière, pendant une heure (55 minutes en fait). Le premier programme a été vidéoprojeté par les profs et les élèves ont eu à continuer l’activité plus ou moins en autonome (il y a eu des questions entre eux). La dernière question est visiblement de trop, même celle sur la spirale ayant eu un fort taux d’échec. Parmi les erreurs surprenantes, il y a eu le nommage de variables par des expressions comme x+3 ou 2x [3]. Le niveau en calcul formel ne s’est pas révélé suffisant pour permettre de faire le lien entre le programme et les expressions littérales [4], et la distinction entre conjecture et démonstration n’est pas toujours perçue [5]. Enfin, les habituelles contraintes matérielles se sont manifestées, avec 3 plantages avec pertes de données [6].
Au lieu de l’utilitaire bloquement utilisé dans cet article, on peut préférer cette version munie d’une fenêtre de sortie, à la fin de laquelle les affichages numériques peuvent être empilés :
























Commentaires