Compter en binaire et algo à gogo avec le robot Thymio

Apprendre à compter
lundi 10 novembre 2014
par  Nathalie CARRIÉ

Le robot Thymio permet de découvrir la programmation de manière très progressive, grâce à une interface de programmation visuelle, couplée à une interface textuelle.

Le robot Thymio II est produit et vendu par l’association Mobsya, et, pour environ une centaine d’euros, on peut le commander ici.
Ce petit robot permet une réelle approche scientifique de la robotique pour nos élèves, possédant de nombreux capteurs (capteurs infrarouge, capteur de température, micro, capteurs mesurant les 3 composantes de l’accélération, 5 boutons on-off) et de nombreux actuateurs (nombreuses leds dont une led RGB qui permet donc d’appréhender le mélange des couleurs, un moteur sur chaque roue, un haut-parleur). L’apprentissage de sa programmation se fait de manière très progressive, grâce à une interface de programmation visuelle, qui crée les lignes de codes correspondantes, ce qui permet d’affiner ensuite le code.

Son site de présentation - et de référence d’ailleurs -, permet assez rapidement de réaliser le champ d’applications potentielles qu’il vous sera possible de réaliser grâce à ce petit robot.

Au lycée Antoine Roussin, nous en avons commandé 5 afin de pouvoir les utiliser dès la rentrée 2013 en spécialité ISN en Terminale S.
Un projet Bac a d’ailleurs été réalisé sur Thymio. Les élèves ont réalisé un suivi de ligne à l’aide du robot. Une vidéo est visible ici.

Vous pouvez voir ce schéma pour avoir une liste complète de ses capteurs et actuateurs.
Thymio permet une approche multi-disciplinaire de la robotique, et c’est ce qui nous a réellement séduits, mon collègue de physique et moi-même.

Et, cerise sur le gâteau, Thymio II est un projet open source et open hardware !

Nous venons d’en commander 6 de plus, afin de les utiliser dès la seconde...

Balbutiements

Au démarrage, le Thymio possède un certain nombre de comportements usines.

Au début de l’utilisation du Thymio avec les élèves, nous leur avons demandé d’illustrer au maximum de commentaires les programmes qu’ils lisaient, et d’écrire dans la mesure du possible des algorithmes décrivant les comportements du robot.

Voici un exemple de programme du Thymio parlant anglais illustré de commentaires :

La deuxième page de commentaires se trouve ici.

Je voudrais maintenant simplement illustrer le tutoriel de prise en mains du robot.

Ballets en couleur


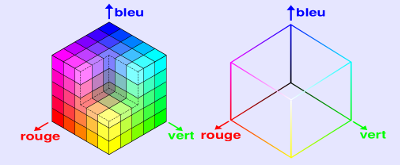
Grâce à la led RGB, on pourra commencer à mélanger les couleurs.

On pourra aussi faire des programmes de base qui consistent à tester divers comportements du Thymio.
Il peut vous suivre comme un petit chien, ou au contraire Thymio vous fuira comme la peste.
Il peut éviter de tomber de la table, etc...

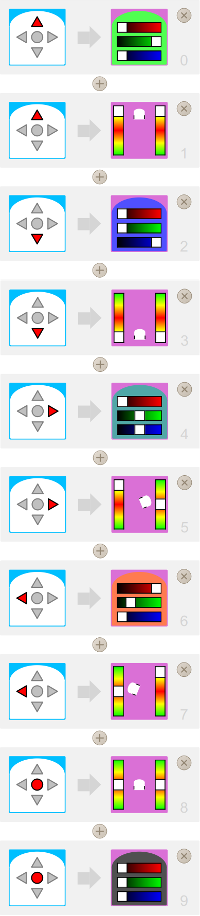
Premier ballet...
... ou Première implémentation du Si... Alors... , avec activation des moteurs.

Le code source sur l’image ci-dessus est automatiquement généré, dès que l’on active des couples d’événements-action dans l’interface de programmation visuelle (VPL). Il peut bien évidemment être nettoyé.

En activant le mode avancé de programmation visuelle du Thymio, on a accès à un minuteur, et à des boutons d’état (qui activent en fait des leds). Cela va nous permettre d’améliorer le programme précédent et d’amorcer un ballet du Thymio qui devient petit à petit un petit robot danseur...

Première boucle infinie
Faisons tout d’abord réaliser une boucle infinie au robot, rendue possible grâce au timer (premier exercice sur les boucles du tutoriel) :

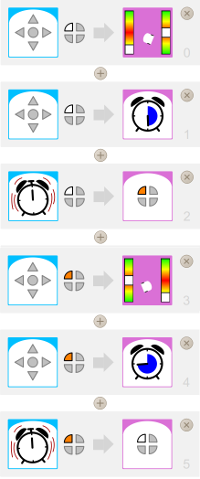
Deuxième ballet

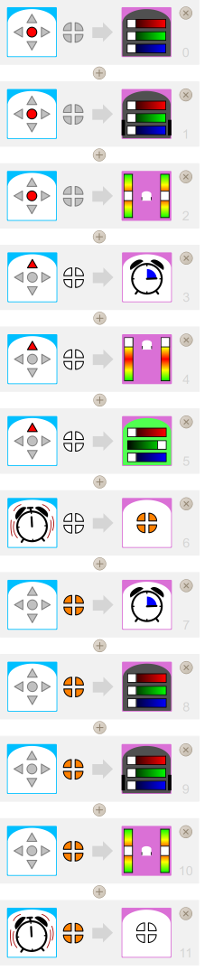
Et voici un début de programme pour un joli ballet :

Ici, l’intervention de l’humain est nécessaire, mais on peut très rapidement améliorer ce programme pour qu’une intervention humaine ne soit plus nécessaire, en mixant par exemple les deux programmes précédents...
Le ballet complet se trouve dans le port-folio de cet article car, seule une direction est implémentée sur l’image ci-dessus.

Exercice : Créer un comportement du robot correspondant à cette image puis simplifier le code source au maximum, car l’interface VPL crée des redondances dans le code, à chaque fois par exemple que l’on teste la même condition (plusieurs if pour la même condition, c’est inutile, il faudra tout mettre dans le même bloc).

Compter avec le Thymio

Ce qui m’intéresse ici, c’est de compter avec Thymio. Le Thymio possède un cercle de 8 leds sur sa face supérieure. Avec 4 leds seulement, on peut décrire 16 états différents, et donc compter en binaire (led éteinte = 0, led allumée = 1) en base 16.

Compter en unaire modulo 2

On va afficher le reste de la division euclidienne d’un nombre par 2.
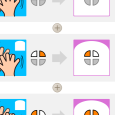
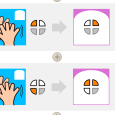
On choisit une led. Elle sera éteinte (blanc) si on tape dans les mains un nombre pair de fois et allumée (orange) si on tape dans les mains un nombre impair de fois.

 
var state[4] = [0,0,0,0]
var new_state[4] = [0,0,0,0]

mic.threshold = 250
call sound.system(-1)
call leds.top(0,0,0)
call leds.bottom.left(0,0,0)
call leds.bottom.right(0,0,0)
call leds.circle(0,0,0,0,0,0,0,0)

sub display_state
	call leds.circle(0,state[1]*32,0,state[3]*32,0,state[2]*32,0,state[0]*32)

onevent mic
	if state[0] == 0 then
		new_state[0] = 1
	end
	if state[0] == 1 then
		new_state[0] = 0
	end

	call math.copy(state, new_state)
	callsub display_state

onevent buttons
	if button.center == 1 then
		new_state[0] = 0
	end

	call math.copy(state, new_state)
	callsub display_state

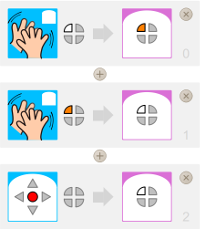
Compter en unaire modulo base 4

On va afficher le reste de la division euclidienne d’un nombre par 4.
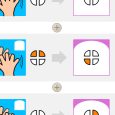
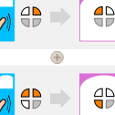
Il faut donc falloir choisir 3 leds car il y a quatre états possibles : 0, 1, 2, 3.

 
var state[4] = [0,0,0,0]
var new_state[4] = [0,0,0,0]

mic.threshold = 250
call sound.system(-1)
call leds.top(0,0,0)
call leds.bottom.left(0,0,0)
call leds.bottom.right(0,0,0)
call leds.circle(0,0,0,0,0,0,0,0)

sub display_state
	call leds.circle(0,state[1]*32,0,state[3]*32,0,state[2]*32,0,state[0]*32)

onevent buttons
	if button.center == 1 then
		new_state[0] = 0
		new_state[1] = 0
		new_state[2] = 0
		new_state[3] = 0
	end

	call math.copy(state, new_state)
	callsub display_state

onevent mic
	if state[0] == 0 and state[1] == 0 and state[2] == 0 and state[3] == 0 then
		new_state[0] = 0
		new_state[1] = 1
		new_state[2] = 0
		new_state[3] = 0
	end
	if state[0] == 0 and state[1] == 1 and state[2] == 0 and state[3] == 0 then
		new_state[0] = 0
		new_state[1] = 1
		new_state[2] = 0
		new_state[3] = 1
	end
	if state[0] == 0 and state[1] == 1 and state[2] == 0 and state[3] == 1 then
		new_state[0] = 0
		new_state[1] = 1
		new_state[2] = 1
		new_state[3] = 1
	end
	if state[0] == 0 and state[1] == 1 and state[2] == 1 and state[3] == 1 then
		new_state[0] = 0
		new_state[1] = 0
		new_state[2] = 0
		new_state[3] = 0
	end

	call math.copy(state, new_state)
	callsub display_state

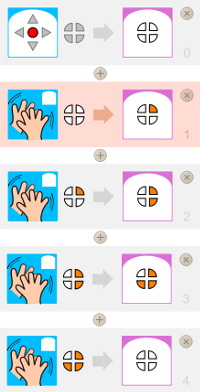
Compter en base 4 en représentation binaire

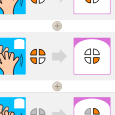
Il n’y a plus besoin que de deux leds pour représenter les nombres de 0 à 3 en base 2.

 
var state[4] = [0,0,0,0]
var new_state[4] = [0,0,0,0]

mic.threshold = 250
call sound.system(-1)
call leds.top(0,0,0)
call leds.bottom.left(0,0,0)
call leds.bottom.right(0,0,0)
call leds.circle(0,0,0,0,0,0,0,0)

sub display_state
	call leds.circle(0,state[1]*32,0,state[3]*32,0,state[2]*32,0,state[0]*32)

onevent buttons
	if button.center == 1 then
		new_state[0] = 0
		new_state[1] = 0
	end

	call math.copy(state, new_state)
	callsub display_state

onevent mic
	if state[0] == 0 and state[1] == 0 then
		new_state[0] = 0
		new_state[1] = 1
	end
	if state[0] == 0 and state[1] == 1 then
		new_state[0] = 1
		new_state[1] = 0
	end
	if state[0] == 1 and state[1] == 0 then
		new_state[0] = 1
		new_state[1] = 1
	end
	if state[0] == 1 and state[1] == 1 then
		new_state[0] = 0
		new_state[1] = 0
	end

	call math.copy(state, new_state)
	callsub display_state

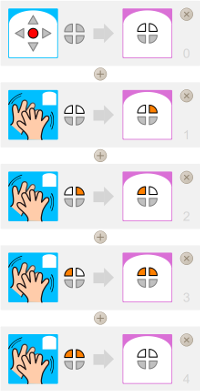
Compter en base 8 en représentation binaire

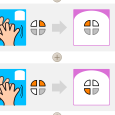
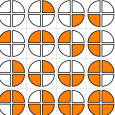
On aura cette fois besoin de trois leds pour représenter les nombres de 0 à 7 en base 2.

 
var state[4] = [0,0,0,0]
var new_state[4] = [0,0,0,0]

mic.threshold = 250
call sound.system(-1)
call leds.top(0,0,0)
call leds.bottom.left(0,0,0)
call leds.bottom.right(0,0,0)
call leds.circle(0,0,0,0,0,0,0,0)

sub display_state
	call leds.circle(0,state[1]*32,0,state[3]*32,0,state[2]*32,0,state[0]*32)

onevent buttons
	if button.center == 1 then
		new_state[0] = 0
		new_state[1] = 0
		new_state[2] = 0
		new_state[3] = 0
	end

	call math.copy(state, new_state)
	callsub display_state

onevent mic
	if state[0] == 0 and state[1] == 0 and state[2] == 0 and state[3] == 0 then
		new_state[0] = 0
		new_state[1] = 1
		new_state[2] = 0
		new_state[3] = 0
	end
	if state[0] == 0 and state[1] == 1 and state[2] == 0 and state[3] == 0 then
		new_state[0] = 1
		new_state[1] = 0
		new_state[2] = 0
		new_state[3] = 0
	end
	if state[0] == 1 and state[1] == 0 and state[2] == 0 and state[3] == 0 then
		new_state[0] = 1
		new_state[1] = 1
		new_state[2] = 0
		new_state[3] = 0
	end
	if state[0] == 1 and state[1] == 1 and state[2] == 0 and state[3] == 0 then
		new_state[0] = 0
		new_state[1] = 0
		new_state[2] = 1
		new_state[3] = 0
	end
	if state[0] == 0 and state[1] == 0 and state[2] == 1 and state[3] == 0 then
		new_state[0] = 0
		new_state[1] = 1
		new_state[2] = 1
		new_state[3] = 0
	end
	if state[0] == 0 and state[1] == 1 and state[2] == 1 and state[3] == 0 then
		new_state[0] = 1
		new_state[1] = 0
		new_state[2] = 1
		new_state[3] = 0
	end
	if state[0] == 1 and state[1] == 0 and state[2] == 1 and state[3] == 0 then
		new_state[0] = 1
		new_state[1] = 1
		new_state[2] = 1
		new_state[3] = 0
	end
	if state[0] == 1 and state[1] == 1 and state[2] == 1 and state[3] == 0 then
		new_state[0] = 0
		new_state[1] = 0
		new_state[2] = 0
		new_state[3] = 0
	end

	call math.copy(state, new_state)
	callsub display_state

Compter en base 16 en représentation binaire !

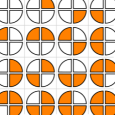
On aura cette fois besoin de quatre leds pour représenter les nombres de 0 à 15 en base 2.

 
var state[4] = [0,0,0,0]
var new_state[4] = [0,0,0,0]

mic.threshold = 250
call sound.system(-1)
call leds.top(0,0,0)
call leds.bottom.left(0,0,0)
call leds.bottom.right(0,0,0)
call leds.circle(0,0,0,0,0,0,0,0)

sub display_state
	call leds.circle(0,state[1]*32,0,state[3]*32,0,state[2]*32,0,state[0]*32)

onevent buttons
	if button.center == 1 then
		new_state[0] = 0
		new_state[1] = 0
		new_state[2] = 0
		new_state[3] = 0
	end

	call math.copy(state, new_state)
	callsub display_state

onevent mic
	if state[0] == 0 and state[1] == 0 and state[2] == 0 and state[3] == 0 then
		new_state[0] = 0
		new_state[1] = 1
		new_state[2] = 0
		new_state[3] = 0
	end
	if state[0] == 0 and state[1] == 1 and state[2] == 0 and state[3] == 0 then
		new_state[0] = 1
		new_state[1] = 0
		new_state[2] = 0
		new_state[3] = 0
	end
	if state[0] == 1 and state[1] == 0 and state[2] == 0 and state[3] == 0 then
		new_state[0] = 1
		new_state[1] = 1
		new_state[2] = 0
		new_state[3] = 0
	end
	if state[0] == 1 and state[1] == 1 and state[2] == 0 and state[3] == 0 then
		new_state[0] = 0
		new_state[1] = 0
		new_state[2] = 1
		new_state[3] = 0
	end
	if state[0] == 0 and state[1] == 0 and state[2] == 1 and state[3] == 0 then
		new_state[0] = 0
		new_state[1] = 1
		new_state[2] = 1
		new_state[3] = 0
	end
	if state[0] == 0 and state[1] == 1 and state[2] == 1 and state[3] == 0 then
		new_state[0] = 1
		new_state[1] = 0
		new_state[2] = 1
		new_state[3] = 0
	end
	if state[0] == 1 and state[1] == 0 and state[2] == 1 and state[3] == 0 then
		new_state[0] = 1
		new_state[1] = 1
		new_state[2] = 1
		new_state[3] = 0
	end
	if state[0] == 1 and state[1] == 1 and state[2] == 1 and state[3] == 0 then
		new_state[0] = 0
		new_state[1] = 0
		new_state[2] = 0
		new_state[3] = 1
	end
	if state[3] == 1 then
		new_state[1] = 1
		new_state[3] = 1
	end
	if state[1] == 1 and state[3] == 1 then
		new_state[0] = 1
		new_state[1] = 0
		new_state[3] = 1
	end
	if state[0] == 1 and state[3] == 1 then
		new_state[0] = 1
		new_state[1] = 1
		new_state[3] = 1
	end
	if state[0] == 1 and state[1] == 1 and state[3] == 1 then
		new_state[2] = 1
		new_state[3] = 1
	end
	if state[2] == 1 and state[3] == 1 then
		new_state[1] = 1
		new_state[2] = 1
		new_state[3] = 1
	end
	if state[1] == 1 and state[2] == 1 and state[3] == 1 then
		new_state[0] = 0
		new_state[1] = 1
		new_state[2] = 1
		new_state[3] = 1
	end
	if state[0] == 0 and state[1] == 1 and state[2] == 1 and state[3] == 1 then
		new_state[0] = 1
		new_state[1] = 1
		new_state[2] = 1
		new_state[3] = 1
	end
	if state[0] == 1 and state[1] == 1 and state[2] == 1 and state[3] == 1 then
		new_state[0] = 0
		new_state[1] = 0
		new_state[2] = 0
		new_state[3] = 0
	end

	call math.copy(state, new_state)
	callsub display_state

Exercices :

  1. Pour compter en unaire modulo base 4, il suffit de trois leds. De combien de leds a-t-on besoin pour compter en base 8 ? Expliquer. Réaliser le programme.
  2. La partie « Compter en base 16 en représentation binaire » ne nécessite que quatre leds pour représenter les nombres de 0 à 15 en base 2. Que peut-on, faire si on utilise huit leds ? Expliquer le principe. (pas besoin du Thymio ici...)

Addition en binaire

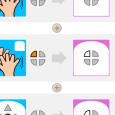
Si on ajoute 1 à un nombre en binaire qui finit par 0, ce 0 devient 1.
Si on ajoute 1 à un nombre en binaire qui finit par 1, ce 1 devient 0, et il y a un effet sur les nombres précédents..
L’arbre ci-dessous montre les transitions 0 → 1 et 1 → 0 pour l’addition.

 
var state[4] = [0,0,0,0]
var new_state[4] = [0,0,0,0]

mic.threshold = 250
call sound.system(-1)
call leds.top(0,0,0)
call leds.bottom.left(0,0,0)
call leds.bottom.right(0,0,0)
call leds.circle(0,0,0,0,0,0,0,0)

sub display_state
	call leds.circle(0,state[1]*32,0,state[3]*32,0,state[2]*32,0,state[0]*32)

onevent buttons
	if button.center == 1 then
		new_state[0] = 0
		new_state[1] = 0
		new_state[2] = 0
		new_state[3] = 0
	end

	call math.copy(state, new_state)
	callsub display_state

onevent mic
	if state[1] == 0 then
		new_state[1] = 1
	end
	if state[0] == 0 and state[1] == 1 then
		new_state[0] = 1
		new_state[1] = 0
	end
	if state[0] == 1 and state[1] == 1 and state[2] == 0 then
		new_state[0] = 0
		new_state[1] = 0
		new_state[2] = 1
	end
	if state[0] == 1 and state[1] == 1 and state[2] == 1 and state[3] == 0 then
		new_state[0] = 0
		new_state[1] = 0
		new_state[2] = 0
		new_state[3] = 1
	end
	if state[0] == 1 and state[1] == 1 and state[2] == 1 and state[3] == 1 then
		new_state[0] = 0
		new_state[1] = 0
		new_state[2] = 0
		new_state[3] = 0
	end

	call math.copy(state, new_state)
	callsub display_state

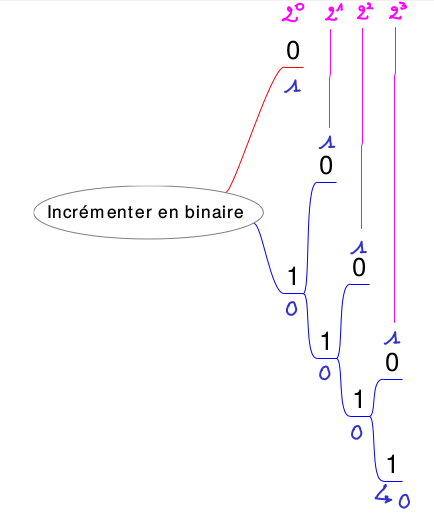
Soustraction en binaire

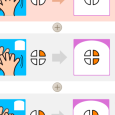
Si on enlève 1 à un nombre en binaire qui finit par 1, ce 1 devient 0.
Si on enlève 1 à un nombre en binaire qui finit par 0, ce 1 devient 0, et il y a un effet sur les nombres précédents.
L’arbre ci-dessous montre les transitions 1 → 0 et 0 → 1 pour la soustraction.

 
var state[4] = [0,0,0,0]
var new_state[4] = [0,0,0,0]

mic.threshold = 250
call sound.system(-1)
call leds.top(0,0,0)
call leds.bottom.left(0,0,0)
call leds.bottom.right(0,0,0)
call leds.circle(0,0,0,0,0,0,0,0)

sub display_state
	call leds.circle(0,state[1]*32,0,state[3]*32,0,state[2]*32,0,state[0]*32)

onevent buttons
	if button.center == 1 then
		new_state[0] = 1
		new_state[1] = 1
		new_state[2] = 1
		new_state[3] = 1
	end

	call math.copy(state, new_state)
	callsub display_state

onevent mic
	if state[1] == 1 then
		new_state[1] = 0
	end
	if state[0] == 1 and state[1] == 0 then
		new_state[0] = 0
		new_state[1] = 1
	end
	if state[0] == 0 and state[1] == 0 and state[2] == 1 then
		new_state[0] = 1
		new_state[1] = 1
		new_state[2] = 0
	end
	if state[0] == 0 and state[1] == 0 and state[2] == 0 and state[3] == 1 then
		new_state[0] = 1
		new_state[1] = 1
		new_state[2] = 1
		new_state[3] = 0
	end
	if state[0] == 0 and state[1] == 0 and state[2] == 0 and state[3] == 0 then
		new_state[0] = 1
		new_state[1] = 1
		new_state[2] = 1
		new_state[3] = 1
	end

	call math.copy(state, new_state)
	callsub display_state

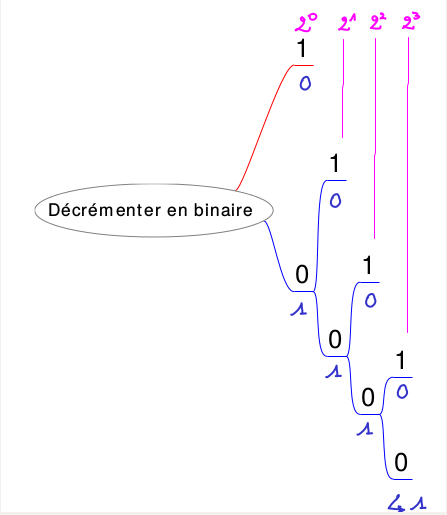
En pratique, il faut affiner les programmes précédents en ajoutant un timer d’enregistrement, afin qu’il n’y ait pas de bruits parasites, ou d’écho qui perturbent le fonctionnement du programme. (Voir par exemple l’addition binaire avec timer).

Thymio et son interface de programmation, un outil idéal pour faire des Sciences

Les nombreux capteurs du Thymio laissent notre imagination sans limite. Ainsi, mon collègue de physique François Ploteau a eu l’idée de demander aux élèves des étalonnages des capteurs de distance et d’accélération.

  1. Étalonnage des capteurs de distance
  2. Étalonnage des capteurs d’accélération du robot Thymio

Une description technique détaillée concernant les capteurs et actuateurs se trouve ici (page essentielle pour ce qui va suivre).
Pour suivre les variables liées aux capteurs, il suffit de regarder la fenêtre Variables de l’interface Aseba de programmation du Thymio, en laissant cochée la variable Auto.

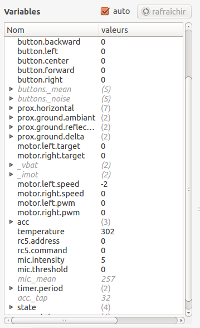
Ces étalonnages ont donné lieu à un recueil de données que nous avons traitées avec une superbe bibliothèque Python : la bibliothèque Pygal (je dis superbe car elle fait de magnifiques courbes...).

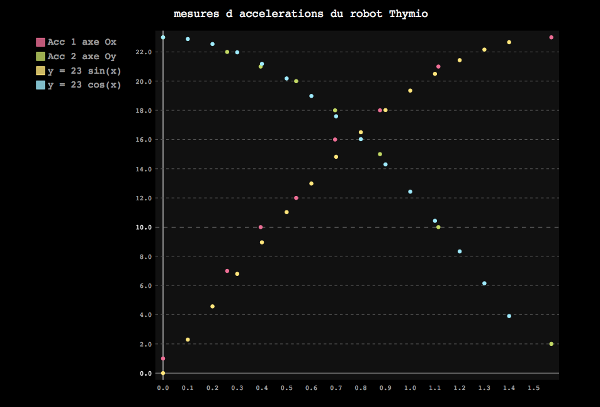
L’interface de programmation du robot permet aussi de voir les graphiques des valeurs enregistrées par les capteurs.

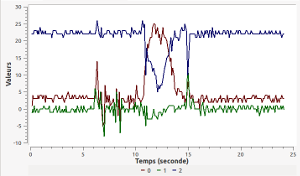
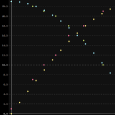
Capteurs d’accélération
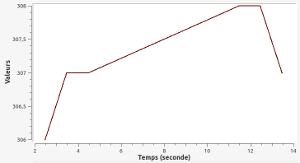
Capteur de température
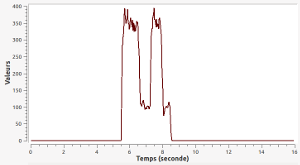
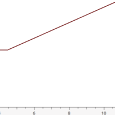
Capteur de vitesse du moteur droit

Limite du langage Aseba, langage de programmation du robot Thymio ?

La description du langage Aseba est donnée dans sa page de référence :
« Aseba est un langage de programmation impératif avec un seul type simple (nombres entiers signés sur 16 bits) et des tableaux. Cette simplicité permet aux développeurs sans connaissances préalables d’un système de type de programmer des comportements ; les nombres entiers étant le type de variable le plus naturel. De plus, les nombres entiers sont particulièrement adaptés aux robots à micro-contrôleurs. »
Jusqu’ici tout va bien.
Aseba nous a aussi donné la possibilité de créer des sous-routines (mot clé sub) pour simplifier le code lorsqu’apparaît une même suite d’opérations à plusieurs endroits dans le code. Malheureusement, cette petite phrase donnée dans la documentation d’Aseba : « Les sous-routines peuvent accéder à toutes les variables. » laisse entendre que les variables du langage sont globales. C’est probablement la raison pour laquelle il n’y a pas la possibilité de créer des fonctions avec passage d’arguments. Personnellement, je trouve que cela complique l’écriture du code.
Par contre, évidemment, l’interface de programmation visuelle, fournie en surcouche pour l’écriture des programmes sur le Thymio est un plus inestimable puisqu’il permet à des enfants de 8 ans par exemple de programmer le robot. La prise en main - devant moi - de l’interface VPL et du robot par un enfant de 8 ans n’a duré que quelques minutes. En une heure, il avait déjà réalisé par lui-même un petit comportement simple, avec marche, recul, rotation du robot, changement de couleurs selon l’événement, timer et réaction sur clappement des mains.


Documents joints

PDF - 196.7 kio
PDF - 196.7 kio

Commentaires

Logo de Okimi
mercredi 25 novembre 2015 à 18h19 - par  Okimi

Bonjour,

Si vous vous intéressez aux robots Thymio II et aux moyens pour les programmer, je vous invite à regarder sur : www.blockly4thymio.net .
Blockly4Thymio est un nouvel environnement pour apprendre, tout en s’amusant, la programmation auprès du jeune publique.

Cet environnement est encore en développement, mais une version d’essai est disponible en téléchargement.

Logo de Sébastien
mercredi 12 novembre 2014 à 05h24 - par  Sébastien

Très bel article. Très complet, merci Nathalie.

Comme dit à la fin de ton article dommage que le langage soit peu abouti. Il faudrait qu’ils essaient de remplacer leur langage par du vrai python par exemple. Avec fonctions, paramètres, variables locales etc. En attendant je pense que Thymio est parfait pour : initiation niveau seconde (utilisation presqu’exclusive de l’interface graphique tout en réfléchissant à l’algorithme pour la résolution d’un problème) et utilisation en ISN sur des TPs croisés (comme celui du plan incliné qui mixe physique/math/info) et exploitation des données recueillies en python. Moins valable pour apprentissage de la programmation niveau ISN.