II. La démonstration peut se faire par récurrence : Par définition L₀ et L₁ sont entiers, et la somme de deux entiers est un entier.

III.

1. Le discriminant de l’équation (-1)²-4×1×(-1)=1+4=5 est strictement positif.
2. Ensuite φ étant solution de l’équation, on a φ²=φ+1. Idem pour l’autre solution ; la somme des deux solutions est l’opposé du coefficient de x, soit 1, et le produit des deux solutions est le coefficient constant de l’équation, soit -1.

IV. Pour n=1, la propriété a été démontrée à la question précédente. Pour n=0 elle revient à dire que 2=1+1 (en élevant un réel à la puissance 0 on trouve 1). L’initialisation est donc faite pour n=0 et n=1. L’hypothèse de récurrence sera donc que la propriété est vraie aux rangs n-2 et n-1. Alors comme L_n=L_n-1+L_n-2, la propriété est aussi vraie au rang n : Par exemple comme φ^n-1+φ^n-2=φ^n-2(φ+1)=φ^n-2×φ²=φⁿ et qu’on peut faire pareil avec l’autre solution de l’équation, on regroupe les termes pour finir la démonstration.

Remarque : Il s’agit en fait d’un problème d’algèbre linéaire (ce qui explique la présence de matrices plus bas) : La suite de Lucas, comme celle de Fibonacci, est élément d’un espace vectoriel de dimension 2, formé par toutes les suites décrites par la même relation de récurrence (mais pas nécessairement les mêmes premiers termes). La formule de Binet consiste à écrire ces suites dans une base formée par des suites géométriques.

V. On a vu à la question précédente que L_n est supérieur à φⁿ. Ce qui peut s’écrire log₁₀L_n≥n×log₁₀φ>n×0,2. Alors si n est supérieur à 5p, log₁₀L_n>p×0,2×5=p cqfd puisque la fonction log₁₀ est croissante.

VI. 1.La formule de Binet donne, a priori, ce script :

from math import *

def lucas1(n):
    if n == 0:
      return 2
    phi = (1+ sqrt(5))/2
    phi2 = (1 - sqrt(5))/2
    return phi**n + phi2**n

mais les valeurs affichées ne sont pas entières ce qui est en contradiction avec la question II. Pourquoi ? Parce que les flottants de Python occupant une place limitée en mémoire machine, il y a des erreurs d’approximation qui donnent des résultats ne coïncidant pas tout-à-fait avec des entiers. Il est donc nécessaire d’opérer un transtypage. Par exemple avec

from math import *

def lucas1(n):
    if n == 0:
      return 2
    phi = (1+ sqrt(5))/2
    phi2 = (1 - sqrt (5))/2
    return int(round(phi**n + phi2**n))

2. L’énoncé propose ce script :

from math import *

def lucas2(n):
    if n == 0:
      return 2
    phi = (1+ sqrt(5))/2
    if n%2 == 0:
        return ceil(phi**n)
    else:
    	return floor(phi**n)

D’après le IV, L_n est la somme de φⁿ et de la puissance n-ième d’un nombre négatif. Donc

• si n est pair, L_n est plus grand que n ;
• si n est impair, L_n est plus petit que n.

Par ailleurs, l’erreur d’approximation consistant à remplacer L_n par φⁿ est une suite géométrique dont la raison a une valeur absolue inférieure à 1 et tend donc vers 0. Comme de plus, le premier terme de cette suite est environ -0,618, les termes suivants sont tous inférieurs à 1 en valeur absolue. En résumé :

• si n est pair, L_n<φⁿ<L_n+1 et L_n est l’arrondi entier par défaut de φⁿ ;
• si n est impair, L_n-1<φⁿ < L_n et L_n est l’arrondi entier par excès de φⁿ.

C’est exactement ce que racontent les lignes 6 à 9 du script.

3. Remarque : L’énoncé prétend que lucas2(36) donne 33385283 mais ce n’est pas vrai avec la version 2 de Python [1]. Or même en maths il y a de multiples excellentes raisons d’utiliser Python 2.7.

Ceci dit, les erreurs d’approximation citées précédemment font que le nombre φ³⁶ qui est très proche de 33385282 est représenté en machine, dans Python 3 tout du moins, comme très légèrement supérieur à ce nombre, et la fonction ceil lui associe 33385283. Une valeur approchée de φ³⁶ est 33385281,99999997 [2] que l’on voit légèrement inférieur à 33385282. En JavaScript, l’arrondi est aussi inférieur à 33385282 [3]. Quant à savoir pourquoi Python 3 arrondit au-dessus là où les autres arrondissent en-dessous, une explication possible est le fait que Python 3 arrondit trop...

VII. 1. Voici le script complété, il ne fait que reprendre celui qui ouvre cet article mais en version programmation fonctionnelle :

from math import *

def lucas3(n):
    if n == 0:
        return 2
    if n == 1:
        return 1
    a, b = 2, 1
    for i in range(n):
        a, b = b, a+b
    return b

2. Si, avant l’exécution de la ligne 7, a=L_i et b=L_i+1 alors après l’exécution de la ligne 7, a=L_i+1 et b=L_i+L_i+1=L_i+2, ce qui démontre par récurrence que les égalités en caractères gras ci-dessus constituent un invariant de boucle. Alors à la sortie de la boucle, on a a=L_n-1 et b=L_n. La fonction lucas3 renvoie donc la valeur exacte de L_n cqfd.

3. Comme la ligne 7 ne comporte qu’une seule addition, et que la boucle est parcourue n fois, il y a n additions qui sont effectuées dans la boucle.

VIII. 1. Pour démontrer la formule, on propose de s’inspirer de Donald Knuth en anticipant un peu sur la question suivante : Le script que voici

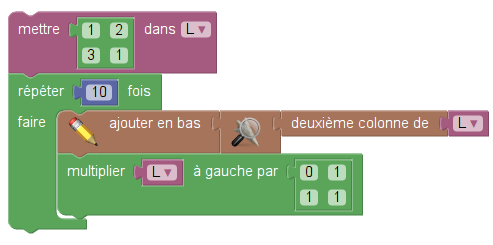
calcule aussi les nombres de Lucas mais deux par deux :

[2, 1]
[1, 3]
[3, 4]
[4, 7]
[7, 11]
[11, 18]
[18, 29]
[29, 47]
[47, 76]
[76, 123]

La démonstration est faite à la question X. Cela signifie qu’avec la matrice A de la question X, la matrice dont les éléments sont L_n, L_n-1, L_n+1 et L_n est le produit de A^n-1 par la matrice de départ dont les éléments sont 1, 3, 2 et 1. Or le déterminant de la matrice est L_n²-L_n+1×L_n-1, le déterminant de A^n-1 est (-1)^n-1 et le déterminant de la matrice de départ est -5 ; Le déterminant du produit est alors 5(-1)ⁿ cqfd [4].

2. En notant φ’ l’autre solution de x²-x-1=0, on a vu que L_n=φⁿ+φ’ⁿ d’où L_n+1=φⁿ⁺¹+φ’ⁿ⁺¹ ; en multipliant ces deux égalités membre à membre, on a L_n×L_n+1=(φⁿ+φ’ⁿ)×(φⁿ⁺¹+φ’ⁿ⁺¹)=L_2n+1+(-1)ⁿ après développement et en utilisant le fait que φ×φ’=-1 ; et en élevant la première des deux égalités au carré, on obtient de manière similaire L_n²=L_2n²×(-1)ⁿ cqfd

IX. 1. Si k est pair, k modulo 2 est nul et l’expression vaut 1-2×0=1 ; si k est impair, k modulo 2 vaut 1 et l’expression vaut 1-2×1=-1. Dans les deux cas, l’expression coïncide avec (-1)^k mais elle est a priori plus rapide à calculer puisqu’elle ne comporte pas d’exponentiation.

2. Le script complété est ici (avec choix de ne pas mettre les parenthèses superflues autour des couples) :

from math import *

def lucas4(n):
    if n == 0:
        return 2, 1
    if n == 1:
        return 1, 3
    k = n//2
    u = 1-2*(k%2)
    a, b = lucas4(k)
    if n%2 == 0:
        return a**2-2*u, a*b-u
    else:
    	return a*b-u, a**2+a*b-3*u

La dernière expression a été obtenue en additionnant les deux égalités du VIII.2

On remarque que le calcul est fait sur deux valeurs successives de la suite, ce qui préfigure le calcul maticiel du X.

3. Si n est égal à 0 ou 1, il n’y a pas d’appels faits à la fonction lucas4. Sinon, autant d’appels sont faits à la fonction lucas4, qu’il y a de divisions par 2 pour aboutir à 0 ou 1. Le nombre d’appels récursifs est donc la partie entière de log₂(n).

X.En multipliant A par V_n (vecteur noté L dans le script Sofus ci-dessus), on obtient pour l’abscisse L_n et pour l’ordonnée L_n-1+L_n=L_n+1. Donc A×V_n-1=V_n. On en déduit par récurrence que V_n=AⁿV₀.

XI. 1. Une solution possible, sans boucle :

def prodMat(M1,M2):
	P = [[0,0],[0,0]]
	P[0][0] = M1[0][0]*M2[0][0]+M1[0][1]*M2[1][0]
	P[0][1] = M1[0][0]*M2[0][1]+M1[0][1]*M2[1][1]
	P[1][0] = M1[1][0]*M2[0][0]+M1[1][1]*M2[1][0]
	P[1][1] = M1[1][0]*M2[0][1]+M1[1][1]*M2[1][1]
	return P

2. Le calcul d’un coefficient de la matrice produit nécessite deux multiplications et une addition. Comme il y a 4 coefficients, en tout cela fait 4 additions et 8 multiplications [5].

3. L’itérateur range(p) boucle p fois donc il y a p appels à la fonction prodMat.

XII. 1. Si n=0, aucune multiplication matricielle n’est effectuée. Si n=1, deux multiplications sont effectuées (une pour R, l’autre pour P). Si n est supérieur à 1, le nombre de divisions par 2 est log₂(n). Et pour chacune de ces divisions par 2, il est effectué une (pour P) ou deux (pour R en plus) multiplications, ce qui fait un total majoré par 2+2log₂(n) cqfd.

2. À chaque passage dans la boucle, P est élevée au carré, donc après i passages dans la boucle P=M²ⁱ

3. Après le 0-ième passage dans la boucle (c’est-à-dire avant d’entrer dans la boucle), n=Σ_j=0^pc_j2^j-0. L’invariant de boucle est donc vrai pour i=0. Par récurrence supposons qu’après i-1 passages dans la boucle on a n=Σ_j=i-1^pc_j2^j-i+1. Le i-ème passage dans la boucle a pour effet de diviser n par 2, et le quotient est Σ_j=i^pc_j2^j-i cqfd.

4. Avant d’entrer dans la boucle on a R=I=M⁰. L’invariant de boucle est donc vrai pour i=0. Par récurrence, on suppose qu’après i passages dans la boucle on a R=M^k avec k=Σ_j=0^i-1c_j2^j. Lors du i+1-ème passage dans la boucle, le chiffre des unités de n est c_i, et si ce chiffre est impair on multiplie R par M²ⁱ⁺¹ d’après le XII2. Après cette multiplication l’exposant k de M dans R a été augmenté de 2ⁱ⁺¹ et k est devenu égal à Σ_j=0ⁱc_j2^j. Si c_i=0 on a aussi k=Σ_j=0ⁱc_j2^j puisque le dernier terme est nul. Ce qui prouve par récurrence le résultat.

5. Le nombre de passages dans la boucle est la partie entière de log₂2. La correction de l’algorithme est une conséquence des questions 3 et 4 : À la sortie de la boucle on a toujours k=Σ_j=0^p-1c_j2^j=n et donc R=Mⁿ.

XIII. Voici une possibilité :

def lucas5(n):
	An = puissanceMatRapide([[0,1],[1,1]],n)
	return An[0][0]*2+An[0][1] 

1. Pour l’instance 1, la salle 0 est allouée à la classe C₀ de 0 à 7 puis à la classe C₂ de 8 à 10. La salle 1 est allouée à la classe C₁ de 2 à 13.

Pour l’instance 2, la salle 0 est allouée à la classe C₀ de 0 à 2 puis à la classe C₂ de 4 à 11 ; la salle 1 est allouée à la classe C₁ de 1 à 7 puis à la classe C₄ de 8 à 11 et la salle 2 est allouée à la classe C₃ de 5 à 6 puis à la classe C₅ de 9 à 13.

2. Pour l’instance 1, la classe C₁ ayant cours en même temps que chacune des deux autres, on ne peut descendre en-dessous des 2 salles allouées.

Pour l’instance 2, il y a un moment (de 5 à 6) où trois classes doivent être allouées simultanément, et le minimum est donc 3. Il est atteint dans la question précédente.

1. L’exemple 1 est représenté par la liste [[0,7],[2,13],[8,10]] et l’exemple 2, par la liste [[0,2],[1,7],[4,11],[5,6],[8,10],[9,13]]

2. Voici un script court, mais il n’est pas certain que ce soit l’attendu :

def insere(l,elt):
	return [x for x in l if x<elt]+[elt]+[x for x in l if x>elt]

Quand à la fonction insereBis dont on suppose que l’on dispose pour la suite, la voici :

def insereBis(LL,li):
	return [x for x in LL if x[0]<li[0]]+[li]+[x for x in LL if x[0]>li[0]]

1. En version non triée, on peut faire avec append :

def traduit(liste_intervalles):
	liste_evts = []
	numero = 0
	for cours in liste_intervalles:
		liste_evts.append([cours[0],numero,0])
		liste_evts.append([cours[1],numero,1])
		numero += 1
	return liste_evts

2. L’agenda du problème 1 est [[0, 0, 0],[2, 1, 0],[7, 0, 1], [8, 2, 0],[10, 2, 1],[13, 1, 1]]

celui du problème 2 est [[0, 0, 0],[1, 1, 0],[2, 0, 1],[4, 2, 0],[5, 3, 0],[6, 3, 1],[7, 1, 1],[8, 4, 0],[9, 5, 0],[10, 4, 1],[11, 2, 1],[13, 5, 1]]

3. On utilise le 1 mais avec insereBis vu ci-dessus, à la place de append :

def agenda(liste_intervalles):
        liste_evts = []
        numero = 0
        for cours in liste_intervalles:
                liste_evts=insereBis(liste_evts,[cours[0],numero,0])
                liste_evts=insereBis(liste_evts,[cours[1],numero,1])
                numero += 1
        return liste_evts

1. Parmi les 4 fonctions :

def valideA(agenda):
	c = 0
	for e in agenda:
		if e[2]==0: c += 1
		else : c -= 1
		if c<0: return False
		else : return True
def valideB(agenda):
	n,c,i,b = len(agenda),0,0,True
	while b and (i<n):
		if agenda[i][2]==0: c += 1
		else : c -= 1
		i += 1
		b = (c>=0)
	return c==0
def valideC(agenda):
	for i in range(len(agenda)):
		if agenda[i][2]==0:
			b = False
			for j in range(i+1, len(agenda)):
				if agenda[j][2]==1: b = True
			if not b: return b
	return True
def valideD(agenda):
	c = 0
	for e in agenda:
		c += 1-2*e[2]
		if c<0: return False
	return c==0

seule la dernière renvoie False s’il y a plus de 1 que de 0 au début de la liste (mais quand même égalité de 1 et de 0). C’est donc la seule réponse correcte.

2. C’est donc cette fonction qu’on se propose d’adapter, avec une variable m qui contient constamment le maximum d’intervalles simultanément couverts jusque là :

def intersectionMax(agenda):
	c,m = 0,0
	for e in agenda:
		c += 1-2*e[2]
		m = max(m,c)
		if c<0: return False
	return m

La variable m est croissante et sa valeur initiale est 0. Elle varie lorsque c dépasse sa valeur actuelle et à la fin de la boucle, elle contient la valeur maximale de c au cours de l’exécution de la boucle. La correction de l’algorithme vient donc de l’invariant de boucle suivant : À tout instant, c est le nombre actuel d’intervalles couverts. C’est un invariant de boucle car c est incrémenté à chaque ouverture d’intervalle, et décrémenté à chaque fermeture d’intervalle.

3. Il suffit de composer les fonctions précédentes :

def nbr_optimal(liste_intervalles):
	return intersectionMax(agenda(liste_intervalles))

1. Erreurs détectées :

• La variable i n’est pas initialisée
• Le test se fait avec « == » et non « = »
• Le test doit porter sur l’égalité avec n-1 et non n
• il manque une négation dans la boucle

Le script corrigé est alors

def plus_petit_vrai(liste):
	n,i = len(liste), 0
	while not liste[i] and (i<n-1): i += 1
	if i==n-1: return -1
	else: return i

2. En fait au lieu de nb_salles = nbr_optimal(liste_intervalles) on aurait pu faire nb_salles = intersectionMax(liste) puisque la variable liste a de toute façon déjà été calculée.

Voici la fonction complétée :

def allocations(liste_intervalles):
	nb_cours = len(liste_intervalles)
	liste = agenda(liste_intervalles)
	nb_salles = nbr_optimal(liste_intervalles)
	salles_dispos = [True]*nb_salles
	alloc = [-1]*nb_cours
	for l in liste:
		if l[2]==0:
			alloc[l[1]] = plus_petit_vrai(salles_dispos)
			salles_dispos[alloc[l[1]]] = False
		else:
			salles_dispos[alloc[l[1]]] = True
	return alloc