Seymour Papert a créé le premier langage informatique conçu pour les enfants, au MIT Artificial Intelligence Laboratory en 1966 : le langage LOGO.
Une équipe du MIT dirigée par Mitchel Resnick a par la suite développé le langage Scratch, inspiré de Squeak, lui-même inspiré de LOGO [1] [2]. Avec le soutien de cette équipe, un fork de Scratch nommé BYOB (Build Your Own Block), devenu Snap! [3] par la suite, a été conçu pour enseigner la théorie de la programmation par une équipe de l’Université de Berkeley (Californie) dirigée par Brian Harvey travaillant en étroite collaboration avec le développeur Jens Mönig. Bernat Bromagosa a ensuite interfacé Snap! avec le monde réel grâce à l’arduino dans Snap4Arduino.

Seymour Papert pensait que programmer un ordinateur peut faciliter chez l’enfant le processus d’apprentissage de sujets tels que les mathématiques et la physique.

Il pensait que les processus mentaux mis en jeux lors de la programmation d’un ordinateur sont fondamentaux dans l’apprentissage des sciences : mathématiques, physique et chimie, technologie...

Dans la plupart des cursus scolaires, on habitue les enfants à suivre un protocole linéaire d’application de techniques afin d’obtenir le résultat attendu : On pourrait dire que l’ordinateur sert à programmer l’enfant. Alors que dans ma vision des choses, l’enfant programme l’ordinateur, et ce faisant, acquiert la maîtrise (...) des éléments de la technologie moderne, tout en établissant un contact intime avec les notions de science, des mathématiques, et de l’art de bâtir des modèles intellectuels. [4]

Les Mathématiques deviennent un outil ultime pour les élèves, grâce à leur implication sensitive dans des Micromondes informatiques créés pour eux. Seymour Papert parlait de plonger les enfants en immersion dans le pays MathLand, un pays dont la langue naturelle serait les mathématiques [5]. Les enfants y seraient plongés au plus jeune âge, pour en apprendre la langue (celle des Mathématiques) plus facilement. Seymour Papert qui a grandi en manipulant des engrenages donnés par son père a construit son imaginaire autour de ces engrenages. Il était intimement persuadé qu’il fallait faire les choses pour les comprendre.

Seymour Papert a donc créé la tortue-robot, la caractéristique la plus connue de LOGO. Seymour Papert décrit la tortue-logo comme un « objet de calcul avec lequel il faut réfléchir. » Les premières tortues LOGO se composaient d’hémisphères de plexiglas qui pouvaient être programmés pour se déplacer sur le plancher. Plus tard les tortues ont inclus un stylo qui pouvait être abaissé pour dessiner. Seymour Papert avait inventé la robotique pédagogique. Notons que le robot Thymio est fortement inspiré de la tortue-logo...

Scratch est une réimplémentation de LOGO avec des blocs graphiques de programmation, à imbriquer les uns à la suite des autres, une grande nouveauté qui libère les élèves de la souffrance syntaxique. Cependant, il est impossible avec Scratch de programmer des fonctions.

Brian Harvey et Jens Moënig, pour remédier à ces limitations, ont écrit BYOB [6], devenu Snap! qui permet enfin la programmation fonctionnelle impossible sous Scratch [7].

L’utilisation de la programmation fonctionnelle permet de simuler facilement le monde réel, à l’aide des Micromondes et des objets qui les constituent.

C’est le but principal de notre projet de recherche-action.

Un exemple concret consiste à créer avec Snap! un Micromonde (incubateur de savoir dixit Seymour Papert) dans lequel les élèves pourraient expérimenter le mouvement newtonien, grâce à des tortues de vitesse et d’accélération qui seraient régies par les trois lois de Newton.

À notre connaissance, les premiers travaux sur l’informatique utilisée comme outil pédagogique, proviennent des recherches de Seymour Papert au MIT Lab. Dans le livre Jaillissement de l’esprit, il fait la synthèse des travaux pédagogiques de Piaget et des connaissances informatiques de l’époque.

On y relève deux idées essentielles :

– Il est possible de prévoir des ordinateurs ainsi concus qu’apprendre à communiquer avec eux puisse être un processus naturel.
– Apprendre à communiquer avec un ordinateur a toutes les chances de modifier la façon dont se déroulent les autres apprentissages. [8]

Si vous n’avez pas lu ce livre essentiel, nous vous invitons à consulter cette excellente fiche de lecture rédigée par Christophe Gragnic.

Le génie de Seymour Papert lorsqu’il a créé LOGO réside pour nous dans les quatre points suivants.

1. L’incarnation : les élèves s’incarnent dans la tortue (Un élève peut facilement se mettre à la place de la tortue : il imagine qu’il est la tortue). Le côté sensitif (kinesthésique) donne du sens (signification) et développe la motivation de l’élève.
2. Jeux dans les Micromondes : c’est le tâtonnement expérimental de Jean Piaget qui devient possible en mathématiques et en physique chimie grâce à la puissance de la simulation informatique.
3. Les problèmes complexes se décomposent en suite de problèmes simples grâce à la programmation fonctionnelle, ce qui mène l’élève vers une pensée organisée et algorithmique.
4. Modification du statut de l’erreur : L’erreur devient visible pour l’élève et lui permet en autonomie d’améliorer sa compréhension du problème. C’est l’ordinateur qui dit à l’élève si ce qu’il a fait est juste ou faux, ainsi le professeur n’a pas à se trouver dans la position de juge du travail de l’élève, mais dans celle d’un accompagnateur de l’apprentissage.

L’idée de cette recherche est d’appliquer la pensée de Seymour Papert en développant la pensée algorithmique chez les élèves.

Cette expérimentation a eu lieu au cours de l’année scolaire 2019-2020 dans les classes de Arnaud Verhille, enseignant en physique/chimie au collège de Sainte-Rose :

➡ En classe de sixième :
– Observation et étude du mouvement des planètes à l’aide du logiciel Snap! (circulaire uniforme)
– Réalisation d’un projet morse avec Snap! pour allier visuel et auditif (lumière, codage)
– Transmission d’information par des signaux lumineux laser en morse.

➡ En classe de cinquième :
– Mesure de temps au chronomètre du smartphone puis calcul des moyennes mesurés pour calculer la vitesse (sous Snap!) sachant que l’élève a couru à l’extérieur sur un parcours de 10 m.
– Acquisition de données et représentation graphique de grandeurs physiques avec Snap4Arduino. (Température, Pression, Photorésistance, Résistance variable)

➡ Club astro du collège :
– Détermination des dates de conjonction Terre - Mars pour savoir quand préparer une mission sur Mars.
– Programmation des robots Thymio en Snap! pour leur donner une autonomie de mouvement en environnement dangereux (la table avec les ravins des bords et la falaise du devant).
– Jouer avec la gravitation. C’est du tâtonnement expérimental des lois de Newton sous forme de « serious game » réalisée sous Snap!

➡ En classe de troisième, l’objectif est de préparer le brevet. Nous avons axé le travail sur :
– Savoir faire les [blocs de] conversions d’unités, ce qui est une difficulté récurrente pour laquelle il faut régulièrement faire des piqûres de rappel chez nos élèves.
– Savoir trouver les 3 formes d’une égalité reliant 3 grandeurs physiques dans une formule du type « P = m x g ». Savoir choisir la forme de l’équation donnant la valeur de la grandeur physique que l’on veut calculer.
– S’entraîner à utiliser les différentes formes de ces équations et pouvoir ensuite les combiner avec les blocs de conversion d’unités réalisés précédemment sous Snap!.

Nous avons gardé à l’esprit le principe Objectif brevet pour lequel les élèves ont réalisé eux-mêmes un formulaire Snap ! qu’ils ont complété tout au long de l’année.
Malheureusement, le grand confinement n’a pas permis plus d’expérimentations pour cette année 2019 - 2020 ...

Cette séance est vraiment très agréable à réaliser avec les élèves. La synergie entre le son et la lumière ainsi que la verbalisation du code morse permet aux enfants d’intégrer les bases de la programmation fonctionnelle tout en s’amusant beaucoup et en s’affirmant car, tout de même, ils viennent d’ordonner à l’ordinateur de prononcer leur propre nom en morse.

Techniquement, Snap4Arduino permet d’interfacer le logiciel de programmation graphique Snap! avec le microcontrôleur Arduino pour permettre le contrôle des LEDs laser et afficher graphiquement la mesure d’une tension aux bornes des photorésistances qui captent cette lumière. L’interface d’Acquisition fonctionne avec Snap4Arduino en utilisant la bibliothèque firmata pour Arduino. L’interval minimal de temps est de l’ordre du dixième de seconde ce qui permet de visualiser de nombreux types de capteurs. (Température, Pression, Photorésistance, Résistance variable)

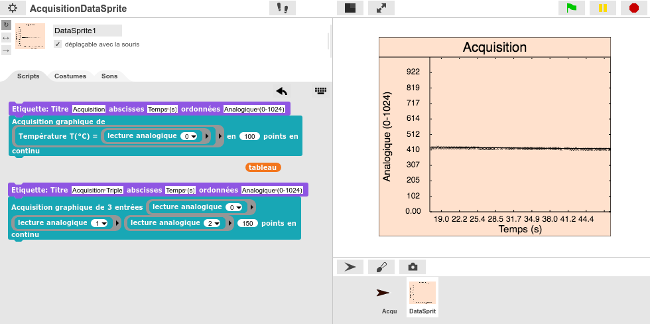
Nous avons donc appliqué cette technique d’acquisition en classe pour permettre aux élèves de visualiser synergiquement cette fonction graphique liée au son, à la lumière laser et à la source du bonheur : l’Amour (LOVE)

Cette visualisation graphique des fonctions peut nous mener des données du monde réel aux données générées par les simulations informatiques des Micromondes Snap!

En sixième, on étudie les mouvements et les trajectoires des planètes du système solaire. Grâce à la programmation fonctionnelle permise par Snap!, le bout de code suivant nous permet de positionner la lune à chaque instant t :

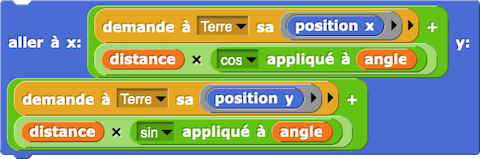
Nous pouvons donc visualiser cette fonction cycloïde qui est la trajectoire de la lune autour du soleil [9].

Voir la simulation, accéder au code source et avoir le contrôle de ce Micromonde :

Le but de ce formulaire est de préparer les élèves aux formules de physique chimie nécessaires pour le brevet des collèges, l’accent étant mis sur une approche fonctionnelle.
Les difficultés répétées des élèves vont nous permettre de cibler les problèmes des conversions d’unités et de manipulation d’expressions algébriques simples.

Afin de faire découvrir la programmation fonctionnelle en physique chimie, nous avons choisi de débuter par l’importante problématique de la conversion d’unités. C’est une excellente occasion pour parler des puissances de 10 et les relier avec les préfixes : kilo, hecto, déca, déci, centi, milli.

Dans cette étape, les élèves découvrent la création de bloc et en même temps la notion de fonction : une fonction avec en entrée la valeur et son unité, et en sortie la valeur convertie dans le système d’unités international.

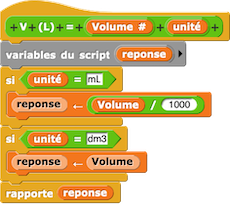
L’exemple ci-dessus est expliqué aux élèves et ils doivent compléter le bloc avec les autres multiples et sous-multiples des unités déjà présentes. Cette étape a un aspect répétitif car il faut recopier et adapter le facteur multiplicatif correspondant à chaque multiple. C’est une excellente chose car les élèves travaillant souvent à plusieurs sur un ordinateur, le travail est réparti, certes, mais visionné par tous. Les plus rapides peuvent commencer à s’occuper des fonctions de conversion d’autres grandeurs physiques.

A la fin, un document Snap! commun est partagé avec toutes les conversions d’unités.

Lors du cours de physique, chaque formule passée en revue a été entrée sous forme de fonction Snap! (bloc avec retour). Cela donne l’occasion à l’élève d’envisager et de coder toutes les formes différentes possibles liées à la formule initiale. Le but étant de se créer un formulaire Snap! qui permet aux élèves d’avoir une vue d’ensemble sur les différentes formes d’une même formule, et de traiter n’importe quel exercice qui leur sera posé.

L’étape suivante, étant donné que les élèves n’auront pas le formulaire Snap! le jour du brevet, est de mémoriser la visualisation des formules au sein de l’interface Snap! tout au long de l’année. Ainsi, l’image mentale du formulaire leur reviendra le jour J.

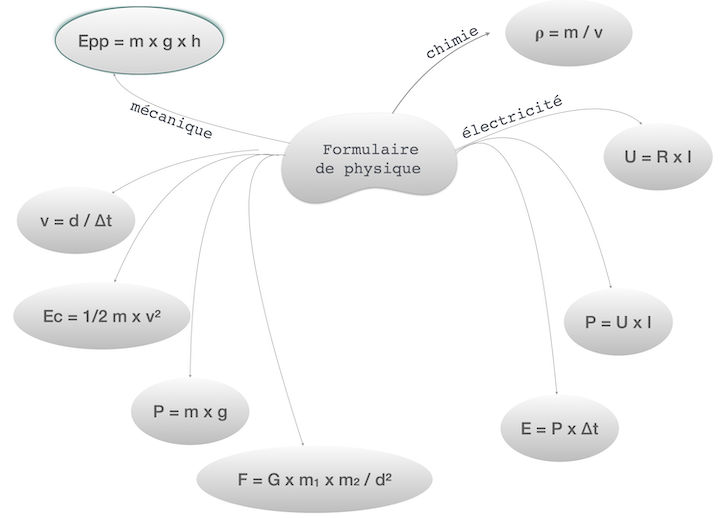
➡ Les relations physiques du formulaire [10]

Toutes les relations mathématiques qui suivent doivent être connues pour le Brevet et travailler sous Snap! permet de lier visuellement les grandeurs physiques à leur unité respective sous la forme d’une fonction :

– Vitesse v = d / Δt

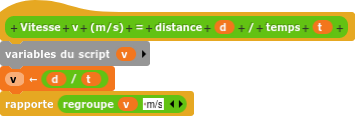
– Masse volumique ρ = m / V

– Poids P = m x g

– Puissance P = U x I

– Énergie cinétique Ec = 1/2 x m x v² (Seule cette forme est exigible en 3^e)

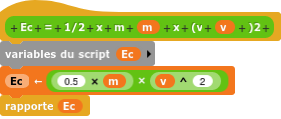
– Énergie E = P x Δt

➡ Les trois formes d’une relation de type « ρ = m / V »

Les élèves ont beaucoup de mal à comprendre qu’il existe trois formes algébrique de cette égalité mathématique et physique. Faire écrire ses différentes formes permet d’insister sur l’importance de ce choix pour résoudre les futurs problèmes.
Bien sûr, il faut écrire les 3 formes pour la majorité des fonctions du paragraphe précédent !

Exemples de résolution d’exercices en utilisant les fonctions précédentes

Précédemment, en cours, nous avons présenté une méthode typique de résolution d’un exercice de troisième :
– Identifier les grandeurs physiques présentes dans l’énoncé et effectuer les conversions d’unités nécessaires pour être dans le système d’unité international.
– Choisir quelle formule et quelle forme de cette formule.
– Faire la fonction calcul de la grandeur physique recherchée ou utiliser cette qui est déjà présente.
– imbriquer les fonctions conversion d’unité dans les fonctions calcul de grandeur physique.
– Lire le résultat en cliquant sur la combinaison de blocs Snap!

Bien sûr, il faudra entraîner les élèves à retrouver les étapes de la résolution de l’exercice sans Snap! en effectuant les calculs sur le papier.

• Soit une marmite à riz de taille moyenne de 600 W qui fonctionne pendant 20 min. Calcule l’énergie consommée en Joules.

• Le téléphone portable : sachant que la batterie de votre téléphone portable chargé peut délivrer une énergie de 0,5 kWh, et que la puissance nécessaire pour jouer est de 200 W, quelle est son autonomie en seconde ? en heures ?

Très rapidement, nous nous sommes rendu compte qu’il était possible, avec peu d’effort, de construire un générateur automatique d’exercice. Avec des images d’illustration adaptés, ça donne le programme suivant. Je conseille de rapidement se rendre sur la forme éditable afin de pouvoir utiliser les fonctions déjà présentes pour obtenir les résultats calculés par Snap!

Toutes les relations physiques (fonctions) et les grandeurs physiques (entrées et sorties de fonction) vues précédemment dans le cours de physique chimie représentent le monde réel. Il est donc possible de simuler ce monde en l’implémentant sous Snap! grâce à l’introduction des équations différentielles en fonction du temps puisqu’elles régissent l’enchaînement des causes et des effets qui est le premier moteur de notre propre Univers.

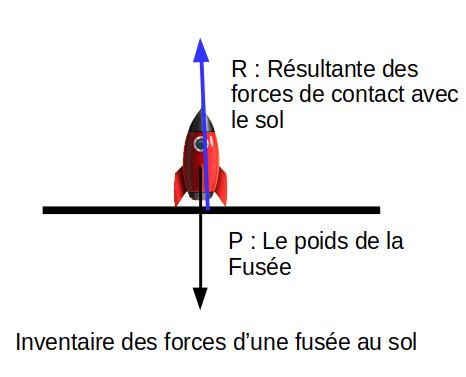
Soyons réalistes, nous n’aborderons pas la construction de ce moteur physique au collège. Ce sera plutôt pour nous le moyen d’animer notre Micromonde. L’objectif étant de permettre le tâtonnement expérimental des lois de Newton dans des conditions inaccessibles en laboratoire comme l’espace. Au collège la schématisation des vecteurs forces appliquées à un objet statique est un élément important du programme et il mérite d’être développé.

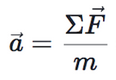
Au lycée, en physique chimie, la méthode d’Euler nous permet de passer d’un instant t à un instant t + dt. C’est une méthode de résolution numérique basique d’équations différentielles en fonction du temps.
En Terminale scientifique, les élèves utilisent la seconde loi de Newton, qui va nous permettre, en faisant l’inventaire des forces, de déterminer l’accélération d’un objet de notre Micromonde.

En utilisant la méthode d’Euler, les lycéens peuvent retrouver à partir de l’accélération, la vitesse puis la position de la tortue. V2D| est une librairie que nous avons réalisé pour l’occasion afin de traiter l’arithmétique des vecteurs 2D.

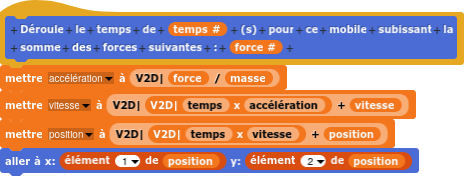
Ce type de tortue est une Dynatortue selon Seymour Papert car on la contrôle en modifiant les forces qui s’appliquent sur elle, c’est-à-dire l’accélération de la tortue [11].

Au collège, nous avons utilisé ce moteur physique pour permettre aux élèves de faire l’inventaire des forces et leur schématisation afin de tester expérimentalement la force de gravitation et les lois de Newton dans les environnements suivants :

– La balle (seul le poids intervient)

Cliquer sur le drapeau vert pour réinitialiser l’intensité de la vitesse et sa direction. De nouvelles conditions initiales donneront d’autres types de paraboles.

– Le décollage de la fusée (Poids + Résistance du sol + Poussée contrôlée par l’élève)

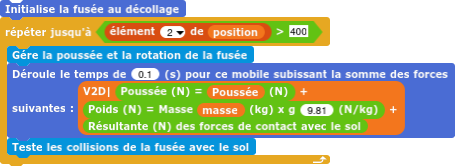
Utiliser les touches flèches ou les touches QZD du clavier pour contrôler votre Dynatortue fusée. Essayer de décoller puis de vous reposer doucement sur la droite ou sur la gauche sans vous écraser à l’atterrissage.

– Mise en orbite de la fusée (Force de gravitation centripète + Poussée contrôlée par l’élève)

Ici, l’objectif est de récupérer le satellite sans être aspiré ou éjecté par la puissance gravitationnelle du trou noir. C’est très difficile car chaque coup de poussée des réacteurs doit être minutieusement dosé et placé pour petit à petit modifier son orbite et se rapprocher de la victoire.

Grâce à Snap!, nous avons pu créer des lutins d’accélération et les élèves du club astro ont pu jouer avec cette simulation [12]. C’est passionnant, je vous conseille de regarder le code source et de tester la première loi de Newton en tentant de survivre dans un champ d’astéroïdes ou tenter de vous poser sur la lune. Mais maintenant il nous faut revenir au réel.

Pour apprendre, les élèves ont besoin de toucher, sentir, entendre, voir. Seymour Papert l’a bien compris puisqu’il a fabriqué une tortue-robot dans le monde réel. Le robot Thymio nous a semblé être l’outil le mieux adapté pour appliquer les idées de Seymour Papert car il possède de nombreux capteurs et actuateurs, et constituera ainsi l’idéal objet de calcul avec lequel les élèves pourront réfléchir.

– Commander 3 robots Thymio-II avec Snap!
– Illustration d’un Micromonde habité de 4 robots Thymio

 [13]

Une librairie à charger dans Snap! pour commander des Thymio est d’ores et déjà disponible sur Github.

Il y a 2600 ans environ vivait le scientifique et mathématicien Pythagore [14]. Il avait des activités ésotériques dans sa secte où l’on pensait que « tout était nombre ». Ils pensaient que les nombres eux mêmes étaient les germes de l’Univers et qu’ils engendraient le cosmos.

Il a donc recherché toute sa vie des relations arithmétiques possédant une signification ésotérique. D’où l’importance du nombre 5 représentant pour lui la quintessence des nombres qu’il trouva partout : dans la gamme Pythagoricienne pentatonique, dans l’étoile à cinq branches qui leur servait de signe de reconnaissance, dans les cinq couleurs de l’arc en ciel, dans les cinq planètes visibles par le monde antique, dans le fameux théorème de Pythagore qui permet d’arpenter, c.a.d. de mesurer toute surface existante grâce à la triangulation du terrain. Trois, quatre et cinq dit-on en créole sur les chantiers.

Pythagore était un proto-scientifique, ses interprétations pouvaient être fantaisistes mais sa méthode était rigoureuse et ses calculs très sérieux pour l’époque.

Son intuition était peut-être que l’état du monde est intégralement décrit par des nombres. Qu’ils sont suffisants pour tout représenter.

On peut se poser légitimement ce type de question quand on observe un nombre comme PI qui est un nombre Univers. Sachant qu’une photo numérique n’est qu’une suite de nombres et que PI contient l’infinité de toutes les suites de nombres. Alors PI contient l’intégralité des photos de chaque instant de la vie de chaque être vivant : terriens, extraterrestres ainsi qu’animaux de compagnie.

Peut-être a-t-il raison finalement, tout est nombre.

Cent ans plus tard, Démocrite d’Abdère proposait plutôt de choisir l’atome comme germe pour engendrer le cosmos.

Il proposait que ces atomes soient soumis à des forces, des interactions à distance comme la gravité mais aussi des interactions de contact qu’il définissait sous la forme d’atomes subtils qui ne se mélangent pas avec les autres ou aux atomes crochus qui restent collés l’un à l’autre par leurs crochets.

Des écrits plus récents suggèrent qu’iI imaginait que l’étincelle originelle de notre monde était dans le clinamen, une légère déviation dans la chute régulière des atomes qui a tout chamboulé et a permis l’apparition du chaos permettant tous les possibles. du cosmos.

Notons que finalement, tout ce que décrit Démocrite dans son clinamen peut aujourd’hui se modéliser et se calculer sous une forme fonctionnelle. La seule véritable limite, c’est la puissance de calcul à notre disposition.

Les relations physiques (électromagnétiques) entre les atomes ne sont qu’un type d’équation, de relation mathématique entre grandeurs physiques.

Plus tard, le philosophe du jardin, Epicure, reprit les idées de Démocrite. Son école Épicurienne devint florissante et bien plus tard, l’un de ses descendants philosophique, le poète Lucrèce, nous offrit un incroyable cadeau, un poème matérialiste et scientifique : De rerum natura (De la nature des choses).

Et que dire du temps ! Sans lui, pas de mouvement ! S’il ne se déroule pas alors tout s’arrête ! Pas de clinamen, pas de chaos, pas d’émergence possible de la vie. Pas de philosophe ni de mathématicien, pas de Snap!

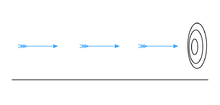
« Dans le paradoxe de la flèche, nous imaginons une flèche en vol. À chaque instant, la flèche se trouve à une position précise. Si l’instant est trop court, alors la flèche n’a pas le temps de se déplacer et reste au repos pendant cet instant. Maintenant, pendant les instants suivants, elle va rester immobile pour la même raison. Si le temps est une succession d’instants et que chaque instant est un moment où le temps est arrêté, le temps n’existe donc pas. La flèche est donc toujours immobile à chaque instant et ne peut pas se déplacer : le mouvement est donc impossible. » Zénon d’Elée

On pourra se délecter du petit livre d’Étienne Klein Le temps existe-t-il ?  [15] dans lequel il conclut :

L’existence avérée de l’antimatière est la preuve matérielle (...) du fait que le temps existe.

Certes, il est possible que le temps n’existe pas. Heureusement, on trouve toujours une solution et cette solution est géniale : On ne peut pas trouver quelque chose qui n’existe pas, mais on peut tendre vers lui, s’en approcher à petit pas de temps, à petits sauts entre les immobilités infinies successives de la trajectoire de cette flèche.

Newton d’un point de vue mécanique et Leibniz ont démontré mathématiquement l’efficacité de leurs incroyables équations différentielles : Nous, humains, sommes maintenant capables de décrire l’enchaînement des causes et des effets avec une précision limitée par nos capteurs et la vitesse de nos calculs lorsque nous dérivons par rapport au temps.

Ivar Ekeland écrit dans Le meilleur des mondes possibles [16] :

Le monde est une machine et la science nous permet de comprendre comment elle fonctionne.

Et si le temps existait et qu’il était le premier moteur immobile ? Celui qui démarre tout, celui qui permet aux forces d’un monde d’agir pour organiser le chaos et permettre l’émergence de poches d’organisation ?

Nous nous limiterons à préciser que c’est justement l’objet de la méthode d’Euler, cette méthode de résolution numérique des équations différentielles, ce moteur qui déroule le temps à petit pas. Si nos équations sont en fonction du temps et basées sur des relations entre des grandeurs physiques, nous pouvons simuler l’action du temps. En précisant les forces qui agissent sur cet objet, le temps simulé se déroule et calcule la position de l’immobilité suivante du paradoxe de Zénon d’Elée.

A cet instant, la donne change et nous sommes capables de créer nos propres mondes : les Micromondes.

Les processus d’apprentissage sont simulables dans le monde des idées par programmation. Ce qui nous amène à réfléchir sur la définition de l’humain. L’humain n’est peut-être que le résultat d’une simulation informatique.

Et si nous étions nous-mêmes dans un simulateur… De nombreux livres et films de science-fiction ont traité ce sujet. Parmi les plus connus, citons comme références culturelles :
– Le livre de science-fiction Simulacron III de Daniel Galouye [17]

– les films Tron [18], Matrix [19] dans lequel la réalité perçue par la plupart des humains est en fait une simulation virtuelle appelée « Matrice », eXistenZ [20] dans lequel nous ne savons plus si nous sommes dans la réalité ou dans le jeu, etc... [21].
– la série Westworld dans laquelle le monde réel et la simulation virtuelle montrent une intrication telle qu’entre androïdes et humains, nous ne savons plus qui code qui...

Toutes ces représentations (simulations) du monde réel nous autorisent à nous poser ces questions très sérieuses :
Serions-nous dans la matrice ? Serions-nous observés et serions-nous nous mêmes les objets (vivants) d’une expérience qui nous dépasse ?