Les jeux en soi ne sont pas nécessairement intéressants mais on peut construire des jeux plus intéressants en juxtaposant des cartes représentant des jeux élémentaires, et analyser le jeu obtenu permet de découvrir les propriétés des nombres, en particulier leur ordre de grandeur.
Matériel
Voici les cartes permettant de construire des jeux (un clic sur l’image ci-dessous donne accès à un pdf à imprimer en couleurs puis découper pour avoir des cartes à jouer) :
Le fichier ci-dessus est à tirer au format A3.
Voici la version A4 :
Et voici la version en noir et blanc (les arcs bleus sont devenus des arcs réservés au dodo, les arcs rouges ceux réservés au gecko) :
Pour créer un jeu, il suffit de poser des cartes de son choix sur le plateau de jeu (une feuille blanche format A3 sur laquelle on peut même coller des cartes dans la version noir et blanc). Mais pour jouer, il faut également des pions, à savoir un pion pour chaque carte choisie.
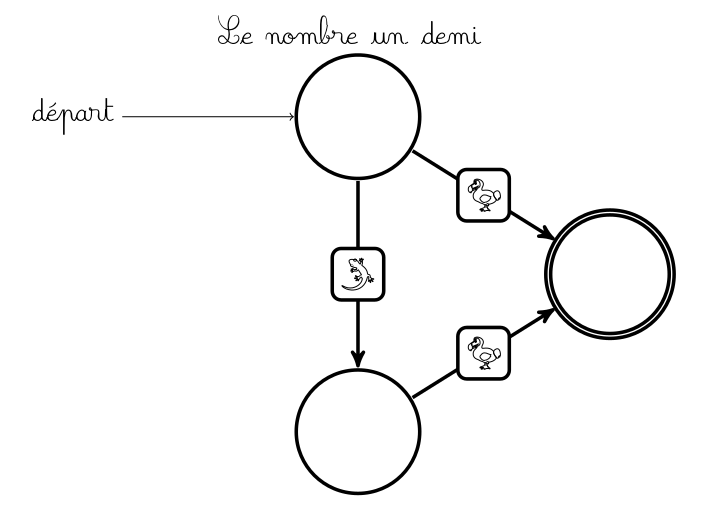
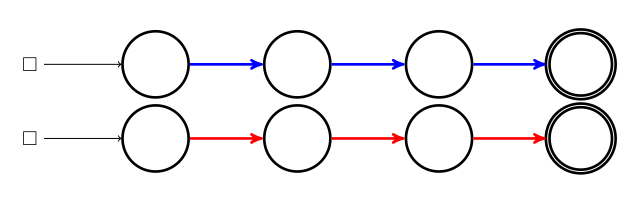
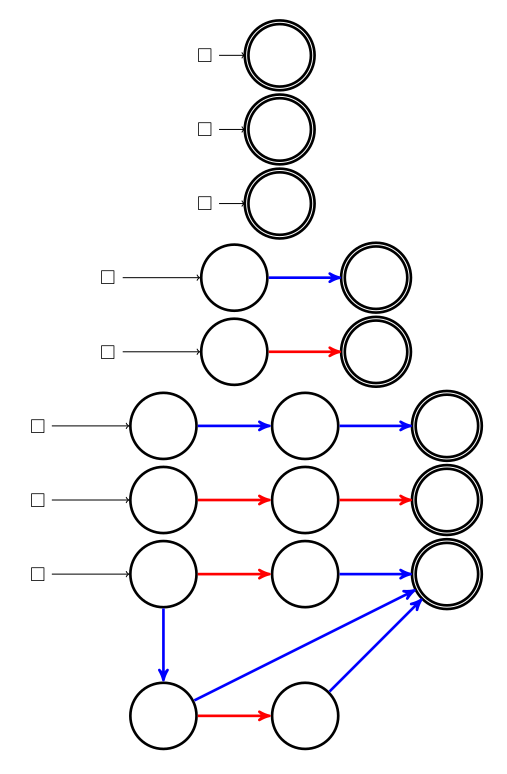
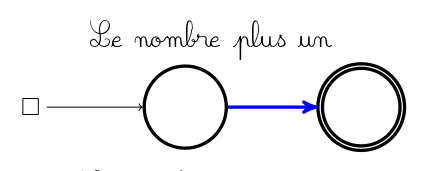
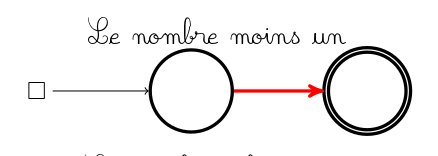
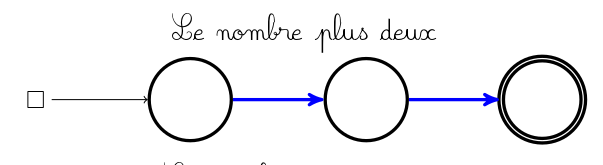
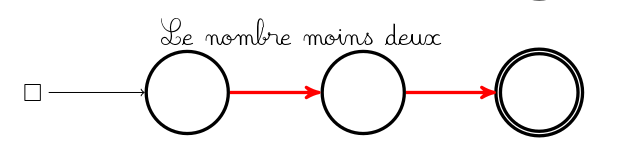
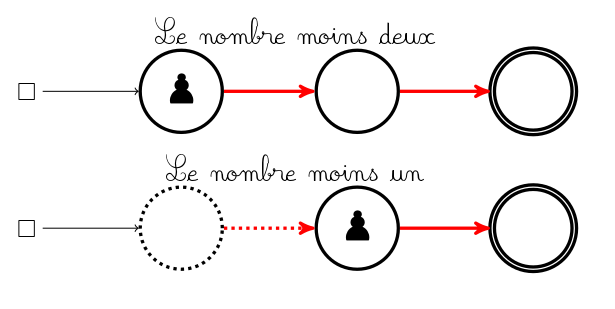
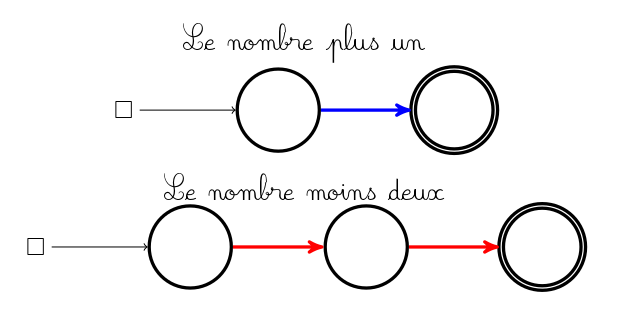
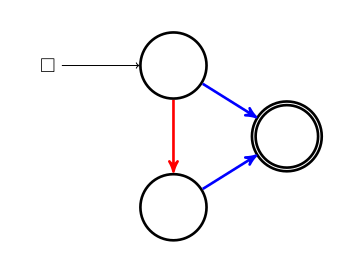
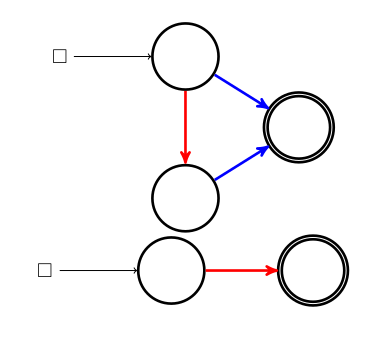
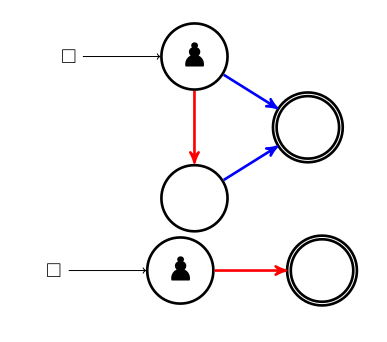
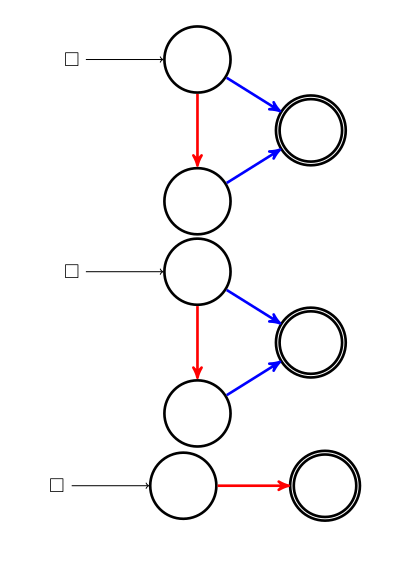
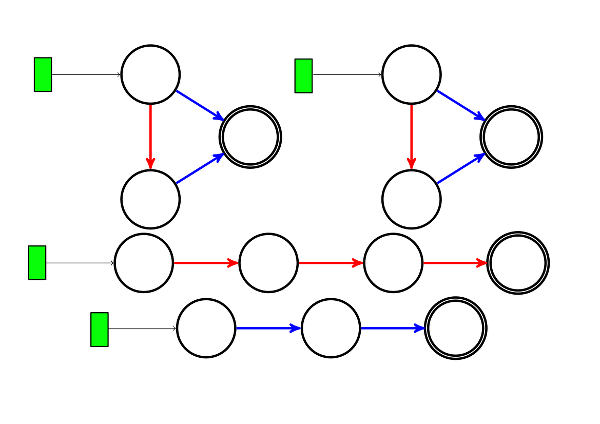
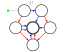
Une petite pancarte indique où poser le pion avant de jouer. En effet il n’y a (pour un graphe connexe du moins) qu’un seul pion pour les deux joueurs. Par contre si c’est aux bleus de jouer, ce pion ne peut glisser que le long d’un arc bleu, et si c’est aux rouges de jouer, le pion ne peut glisser que le long d’un arc rouge :
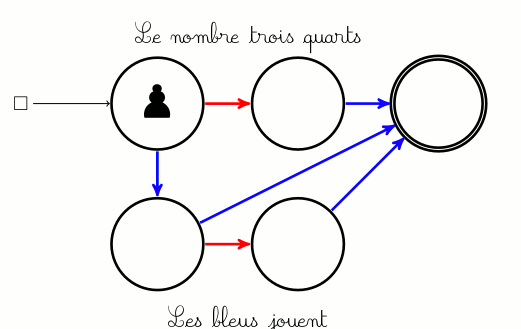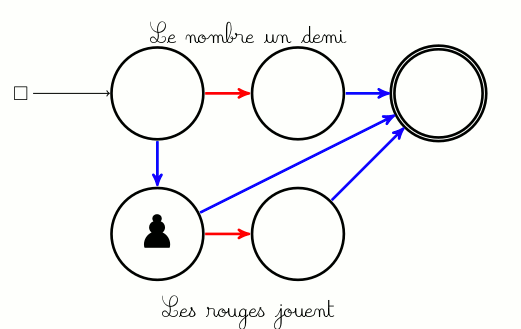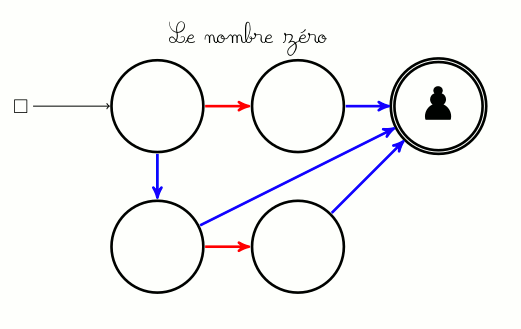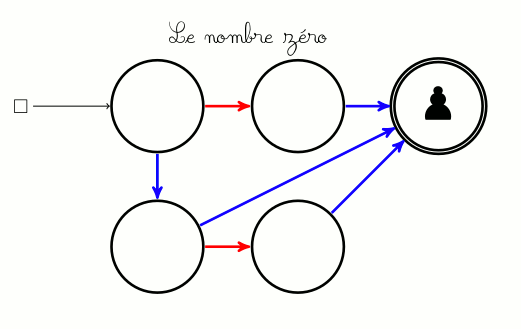
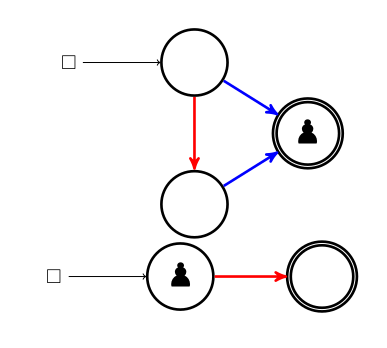
S’il n’y a aucun arc rouge devant le pion alors que c’est aux rouges de jouer, les rouges ont perdu. C’est en particulier le cas lorsque le pion est à l’arrivée et ci-dessus les bleus ont gagné parce qu’ils ont marqué un but en mettant la balle (le pion) dans le panier, mais aussi parce que ce ne sont pas les rouges qui l’ont fait.
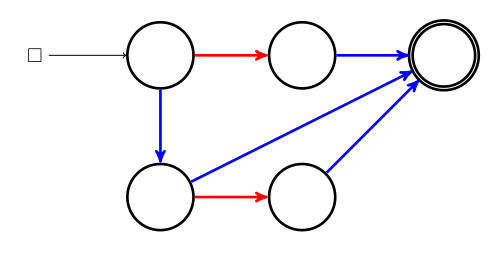
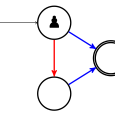
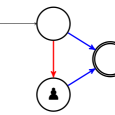
D’ailleurs sur le même graphe, si ce sont les rouges qui jouent en premier, ils perdent aussi :
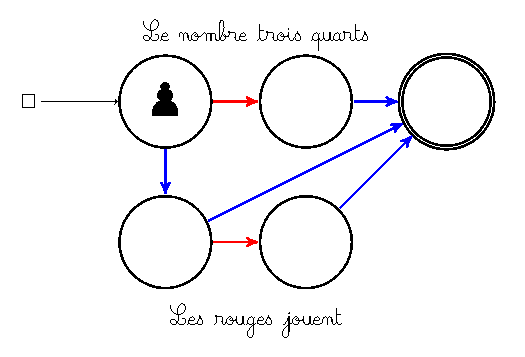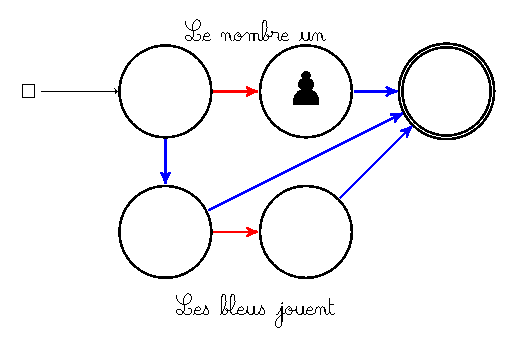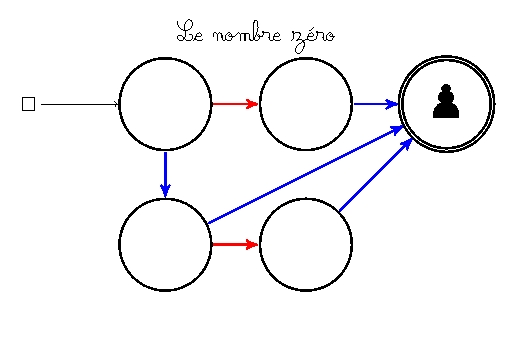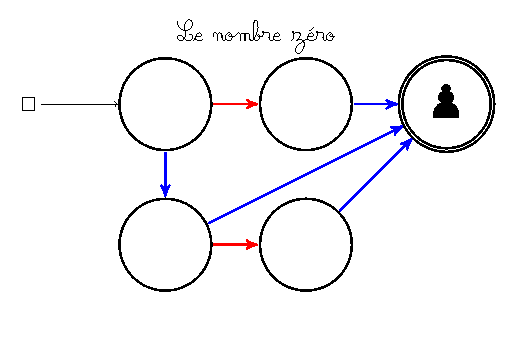
Le jeu ci-dessus est dit positif. Ce qui nous amène à une définition de Conway :
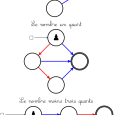
- Si les bleus disposent d’une stratégie gagnante à un jeu, que ce soit à eux de jouer ou pas, le jeu est dit positif et parfois noté en mettant un signe « + » devant sa valeur (par exemple le jeu ci-dessus s’appelle « trois quarts » mais aurait pu s’appeler « plus trois quarts »).
- Si les rouges disposent d’une stratégie gagnante à un jeu, que ce soit à eux de jouer ou pas, le jeu est dit négatif et noté en mettant un signe « - » devant sa valeur.
- Si le prochain joueur, quelle que soit sa couleur, perd le jeu (c’est-à-dire que son adversaire a une stratégie gagnante), le jeu est dit nul ou égal à zéro.
Les jeux trop positifs (trop à l’avantage des bleus) ou trop négatifs sont rapidement jugés ennuyeux, puisque seul un des joueurs y joue durablement. Pour faire durer le jeu, on peut imaginer de donner un handicap au joueur avantagé dans ce jeu en permettant à son adversaire de passer son tour. Par exemple dans le jeu ci-dessous on rétablit l’équilibre en laissant les rouges passer 3 fois leur tour (d’où le nom « trois » donné au jeu) :
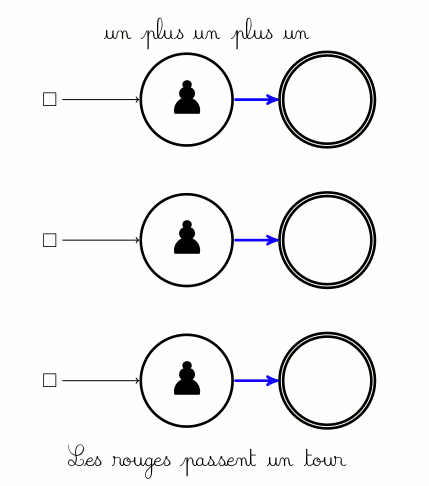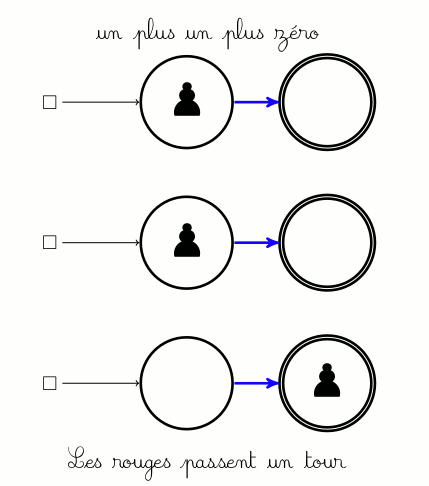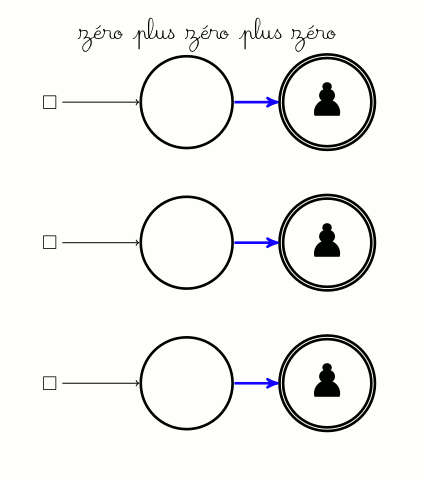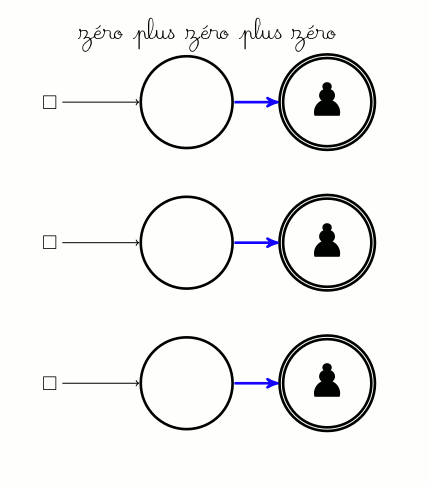
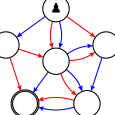
La notion suivante est celle d’addition des jeux. Pour additionner des jeux, il suffit de les mettre côte à côte en plaçant un pion au départ de chaque composante connexe de la somme. Par exemple 1+1+1 est (on le voit en y jouant) le même jeu que ci-dessus :
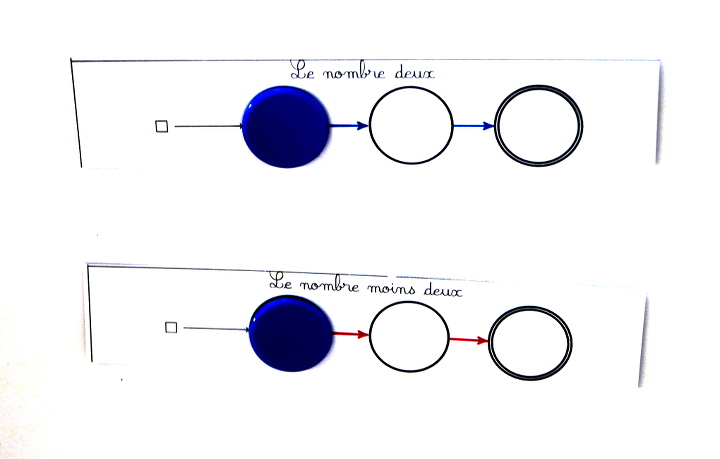
La notion suivante est celle d’opposé d’un jeu. L’opposé d’un jeu s’obtient en échangeant les couleurs rouge et bleue sur le jeu. Par exemple les deux jeux ci-dessous sont opposés (regarder les couleurs) :
Le nombre zéro
Le jeu le plus simple est le jeu zéro. En effet aucun joueur ne peut déplacer le pion :
De ce fait, on peut ajouter autant de copies de ce jeu que l’on veut, sans jamais changer quoi que ce soit au résultat. Ce jeu aussi est zéro :
Du coup, la recherche de termes nuls (égaux à zéro) dans une somme, permet au contraire de simplifier un jeu. Par exemple, comme la somme d’un nombre et de son opposé est égale à zéro, on peut enlever ce genre de graphes d’un jeu, sans modifier l’issue du jeu :
Plus généralement, si le prochain joueur qui joue à un jeu, perd le jeu (parce que son adversaire a une stratégie gagnante) alors le jeu est nul aussi. Ainsi ce jeu
est le même que
De fait, fabriquer un jeu intéressant, revient souvent à faire un jeu
- égal à zéro (il y a une stratégie gagnante pour celui qui joue en deuxième)
- mais dont on ne voit pas au premier coup d’œil que la somme est nulle (la stratégie gagnante ne saute pas aux yeux).
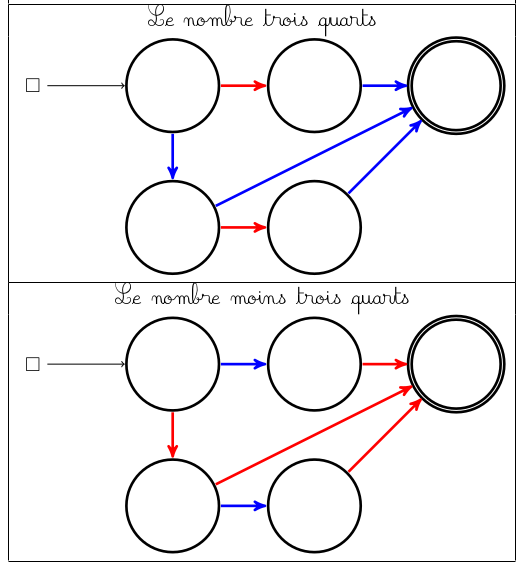
Le jeu zéro a une autre particularité : c’est un nombre.
Les nombres un et deux
Le nombre 1 se retrouve dans deux jeux :
Le nombre plus un, où les bleus ont un coup d’avance (ou de réserve) sur les rouges :
Le nombre moins un, qui est à l’avantage (d’un coup) des rouges :
De façon générale, lorsque les bleus ont un avantage sur les rouges, on met le mot « plus » devant le nombre quantifiant cet avantage pour rappeler que le jeu est positif (à l’avantage des bleus) et lorsqu’un nombre est à l’avantage des rouges (négatif), on met le mot « moins » devant la valeur quantifiant cet avantage.
Le mot « plus » peut être sous-entendu puisque les nombres positifs sont ceux que l’on connaît depuis le cycle 1. Noter qu’il n’y a pas lieu de dire plus zéro ou moins zéro puisque zéro n’est à l’avantage ni des bleus, ni des rouges.
Par exemple lorsque les bleus ont deux coups d’avance sur les rouges, le jeu s’appelle indifféremment deux ou plus deux :
alors que si ce sont les rouges qui ont deux coups d’avance sur les bleus, on dit moins deux :
En fait la valeur d’un graphe est celle qu’on obtient lorsque tout le graphe est jouable, c’est-à-dire quand le pion est encore au départ. Si le pion a avancé, seule une partie du graphe est encore jouable et on peut enlever la partie qui est en pointillés (puisque le pion ne reviendra plus en arrière) ce qui donne de facto un nouveau graphe, avec une nouvelle valeur :
Lorsqu’on joue dans une somme de nombres entiers, chaque mouvement d’un pion le long d’une flèche bleue a pour effet de faire baisser l’un des termes (donc la somme aussi) de 1. Ci-dessus le mouvement du pion a fait passer le jeu, de la valeur 2 à la valeur 1.
Et de même, chaque mouvement d’un pion le long d’une flèche rouge a pour effet de faire augmenter un terme (et donc aussi la somme) d’une unité. Par exemple en passant de moins deux à moins un :
Ainsi, sur une somme de nombres entiers
- faire avancer un pion le long d’une flèche bleue revient au même que faire reculer un pion le long d’une flèche rouge,
- faire avancer un pion le long d’une flèche rouge revient au même que faire reculer un pion le long d’une flèche bleue.
On peut simplifier alors l’analyse de certains jeux, par exemple le nombre plus un :
- si c’est aux bleus de jouer, ils font avancer le pion le long de l’unique flèche bleue, transformant ainsi le jeu en zéro (un moins un) qui est perdant pour les rouges (les prochains à jouer)
- si c’est aux rouges de jouer, ils ont perdu puisqu’il n’y a pas de flèche rouge.
Donc le nombre plus un est positif (à l’avantage des bleus). Mais en lui additionnant moins deux :
le jeu obtenu est à l’avantage des rouges (négatif) :
- si c’est aux bleus de jouer, ils transforment plus un en zéro donc (+1)+(-2) en 0+(-2)=-2 qui est négatif donc gagnant pour les rouges
- si c’est aux rouges de jouer ils transforment moins deux en moins un donc la somme en (+1)+(-1)=0 qui est perdant pour les bleus.
En résumé, la somme de 1 et de l’opposé de 2 est négative. Ce qui signifie que l’avantage que 1 confère aux bleus est plus que compensé par -2, autrement dit, que un est inférieur à deux.
Ce jeu par contre est égal à zéro (le prochain qui joue perd le jeu ; on s’en rend compte en étudiant le jeu, ou simplement en y jouant) :
Or le jeu est égal à (+1)+(+1)+(-2), et dire que 1+1-2=0, c’est dire que 1+1=2.
Avec des nombres entiers, on peut appliquer la typologie de Vergnaud avec des changements d’état :
- un jeu, au sens défini ici, est un état
- jouer c’est effectuer une transformation d’états
L’addition des jeux, lorsqu’on l’applique à des nombres entiers, coïncide avec l’addition des nombres. La technique de raisonnement de Conway consiste à
- étudier le signe de a+(-b) pour comparer a avec b (dire lequel est le plus petit des deux)
- étudier le signe de a+b+(-c) pour comparer a+b avec c, en particulier si on trouve une somme nulle, montrer que a+b=c.
Cette technique permet de montrer l’existence de nombres qui ne sont pas des entiers, comme par exemple
Le nombre 1/2
La carte ci-dessous est positive, comme on s’en rend compte aisément en jouant dessus : soit les bleus commencent et ils marquent le but immédiatement, soit les rouges commencent et les bleus marquent le but juste après.
Mais si additionne le nombre moins un à la carte ci-dessus
on remarque que la somme obtenue est négative. En effet, à partir de la position de départ
- si les bleus commencent, ils ne peuvent que marquer un premier but
et les rouges gagnent en marquant le second but.
- si les rouges jouent en premier, leur stratégie gagnante consiste à faire ceci :
car alors, les bleus n’ont pas d’autre choix que marquer le premier but au coup suivant, laissant les rouges marquer le second but ensuite.
Que la somme
est négative, signifie que le nombre
est inférieur à 1. On a donc là un nombre qui est à la fois positif et plus petit que 1, autrement dit, un nombre qui n’est pas entier. En l’occurence il s’agit d’une fraction, que l’on peut évaleur en étudiant la somme
qui s’avère nulle (celui qui joue en second dispose d’une stratégie gagnante). Or la somme ci-dessus est constituée de deux termes égaux au nombre à estimer, et de moins un. Ce qui signifie qu’en additionnant le nombre avec lui-même, la somme vaut 1 : le nombre est donc égal à 1/2.
Cette technique permet de trouver d’autres fractions comme -1/2, 3/1, 1/4, 3/4, 1/8 etc.
Par contre les fractions représentables par ces jeux sont toutes dyadiques. On ne peut pas obtenir (du moins avec un graphe de taille finie) des fractions comme 1/3 ou 2/5.
Voici la présentation faite au séminaire de l’IREMI du 8 février 2023 :
On y propose la séquence suivante :
En cycle 1
On commence par faire jouer deux joueurs sur une seule carte comme par exemple
(carte créée par des élèves de 6e, valant up qui est un infiniment petit positif)
Cette phase d’appropriation permet de faire travailler la reconnaissance de formes (les flèches) et de couleurs, mais aussi la chronologie du jeu puisqu’il n’y a qu’un pion pour deux joueurs.
Avec un peu d’expérience du jeu, les joueurs peuvent évaluer la qualité de la carte, en dénonçant comme trop injustes les jeux positifs (injustes pour les rouges) et les jeux négatifs (injustes pour les bleus).
Si le temps le permet, on peut ensuite aborder les sommes de deux cartes, comme par exemple :
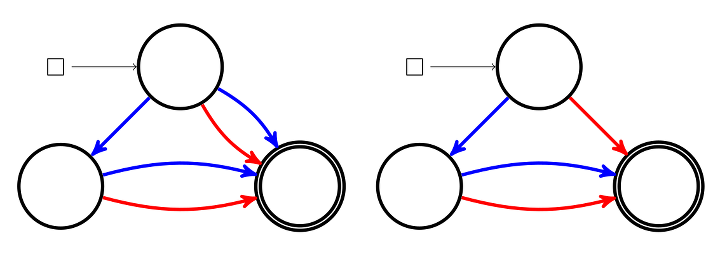
(les joueurs apprennent à choisir le pion qu’ils préfèrent avancer pour faire durer le jeu : notion de stratégie)
Mais le mieux à ce stade est encore de demander aux élèves de construire leurs propres cartes avec des crayons bleu, rouge et noir (et la gomme si on veut améliorer la carte). En effet le programme de cycle 1 recommande de
Réaliser une composition personnelle en reproduisant des graphismes.
On peut aussi concevoir des jeux de ce genre (et les tester) en ligne avec cet outil.
En cycle 2
Après avoir découvert le jeu sur une carte, puis sur deux cartes (avec la notion de signe d’un jeu, d’une somme de deux jeux), on distribue des cartes représentant des nombres entiers, et on demande aux élèves de créer un jeu le plus équitable possible, en posant des cartes sur la carte des cartes.
Zéro
On voit (par l’addition 0+0+(-1)+(+1)+(-2)+(+2)=0) que ce jeu est le plus équitable possible pour une somme d’entiers (le nombre 0). Mais pour le vérifier, les joueurs n’ont qu’à jouer plusieurs fois sur le jeu qu’ils ont créé, pour analyser toutes les situations possibles.
Jeu
Les élèves jouent pour vérifier que l’avantage n’est ni aux rouges, ni aux bleus, mais à ceux qui jouent en deuxième. En fait on pouvait prédire ce résultat en effectuant l’addition (+2)+(-1)+(-1)=0.
Deux
Produit par des élèves de CE 2 :
Moins deux
En séparant les cartes bleues et rouges on voit mieux quel joueur a l’avantage (CE 2) :
En cycle 3
Après avoir découvert le principe du jeu et l’addition des entiers relatifs, les joueurs peuvent également jouer avec des fractions. Il suffit pour cela d’ajouter quelques cartes portant des fractions à celles portant des entiers (le nombre 0 n’est plus nécessaire une fois que les élèves ont compris qu’il ne fait qu’encombrer la carte des cartes ; on dit que 0 est élément neutre pour l’addition). Les élèves de CM2 sont particulièrement créatifs.
zéro
Ce jeu est équitable puisque la somme des 8 cartes est égale à 0. Mais il est possible que sa construction réponde plus à un critère esthétique (recherche de symétrie) qu’à un critère arithmétique.
Entiers
En essayant de mettre beaucoup de cartes sur la carte des cartes, on a du mal à créer un jeu équitable.
Voici un jeu trop avantageux pour les bleus (il vaut 2) :
Celui-la aussi :
Et celui-là par contre est trop à l’avantage des rouges (il vaut -1) :
Fractions
Ce jeu est un peu paradoxal :
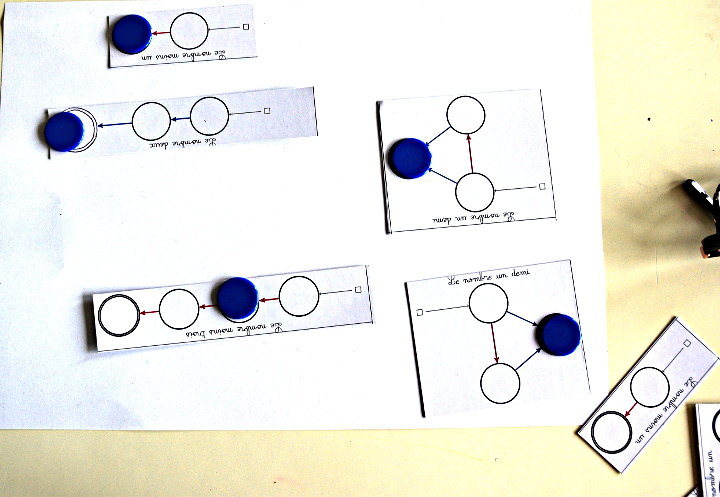
En effet, parmi les 5 cartes posées, il y en a 3 qui sont positives et seulement 2 qui sont négatives. Et pourtant, en jouant à ce jeu, on découvre que les rouges ont une stratégie gagnante. Le calcul de la somme donne d’ailleurs -1 qui est négatif.
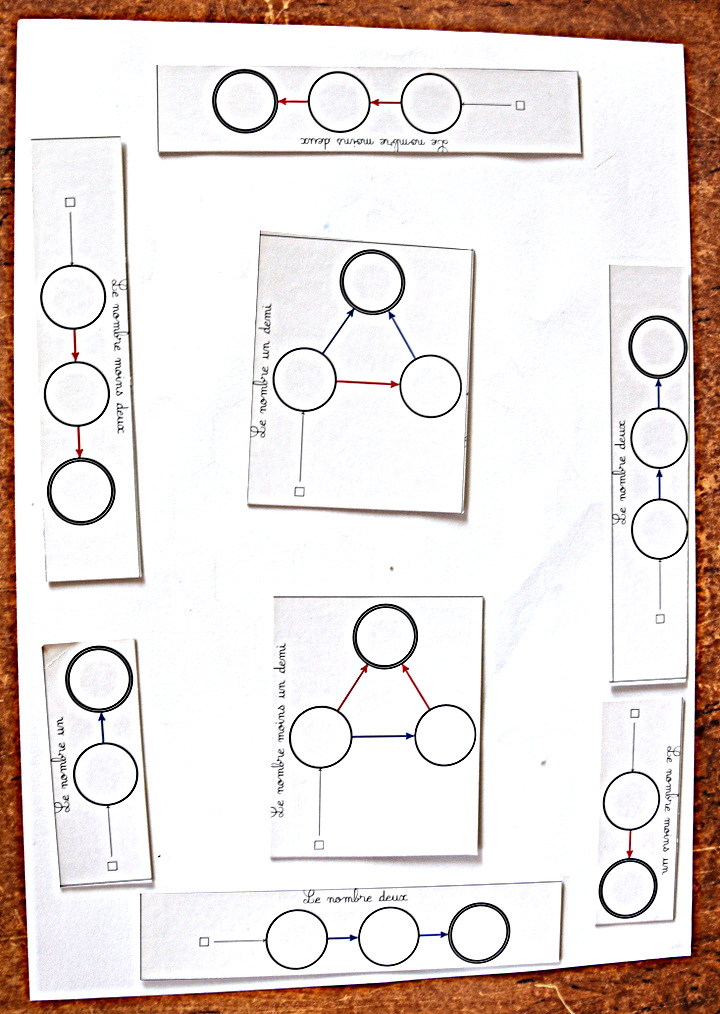
Par contre ce jeu est équilibré (la somme vaut 0 ce qui prouve que 2+1/2+1/2=3) :
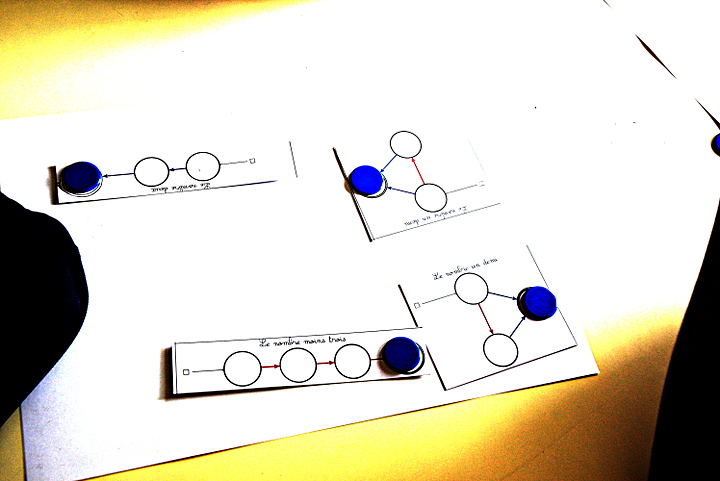
Il est suffisamment beau pour mériter d’être refait en un seul pdf :
Petits nombres
Lors de la semaine des maths, des élèves de 6e ont testé l’activité avec des fractions, et ils ont introduit des améliorations à l’activité :
- Pour voir si un jeu est équitable, on y joue plusieurs fois (avec pierre-papier-ciseaux pour savoir qui commence) et on fait une statistique des parties gagnées par Bleu et par Rouge.
- Une fois qu’on a estimé le signe du jeu, c’est la perdant qui choisit comment modifier le jeu. Pour cela il y a 3 possibilités :
- On peut ajouter une carte qui compense l’avantage du gagnant.
- On peut au contraire retirer une carte qui semble trop avantager le gagnant.
- On peut aussi remplacer une carte trop avantageuse par une autre, moins avantageuse.
Ce processus tend à produire des jeux proches de zéro, dont l’avantage d’un joueur est peu perceptible. Par exemple
Le jeu -0,25 :
(en effet la somme 0,25+0,25-0,75 vaut -0,25)
Encore le jeu -0,25 :
(en effet la somme 3+0,25-3-0,5 vaut -0,25 aussi)
Le jeu 0,25 :
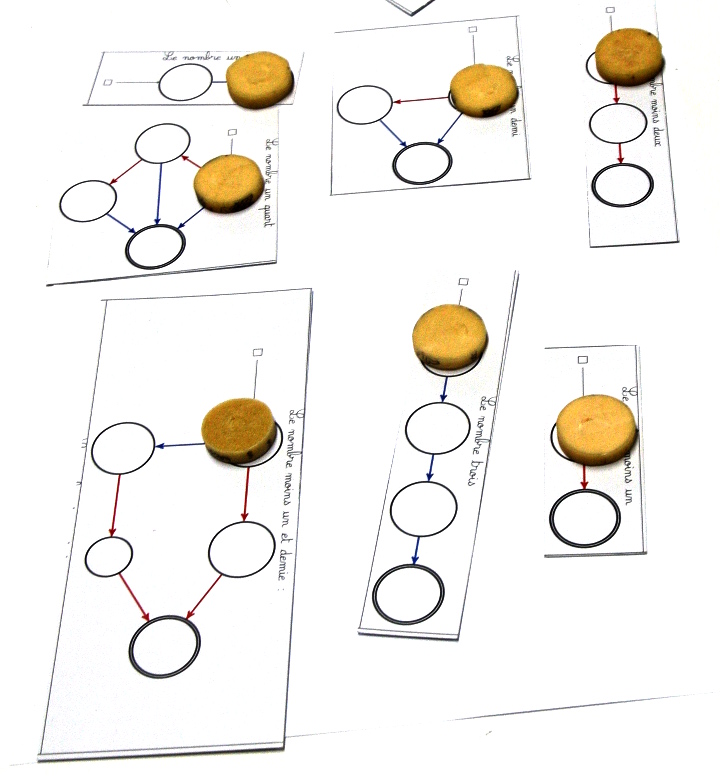
(en effet la somme 1+0,5-2+0,25-1,5+3-1 vaut 0,25)
Ce faisant, les ordres de grandeur des différents nombres intervenant dans le jeu, sont perçus progressivement, et la quête du jeu le plus équitable fait converger la somme vers 0. Voir des exemples dans l’onglet suivant.
Zéro
Voici des sommes nulles réalisées par des élèves de 6e :
– 2,5-1,5+3 :
– 2-1+0,5+1+2+0,25-0,75 :
3+0,5-2-1,5 :
Comme certains élèves ont tendance à vouloir remplir au maximum la carte des cartes, ou à vouloir utiliser toutes les cartes qu’on leur a confiées (plutôt que de choisir les plus pertinentes), il vaut mieux disposer les binômes en cercle, et mettre toutes les cartes entre eux. Ainsi
- il y a trop de cartes pour une feuille A4 et les joueurs sont rapidement obligés d’arrêter d’en ajouter (et incités à en enlever),
- prendre des cartes pour les disposer sur la carte des cartes, c’est en priver les autres joueurs, et la recherche d’un jeu équilibré peut amener à échanger des cartes entre binômes.
En cycle 4
On peut aborder les infinitésimaux en cycle 4, sans nécessairement expliquer la théorie sous-jacente. Par exemple voici un jou équitable (égal à 0) créé par une élève de 4e :
Semaine des maths
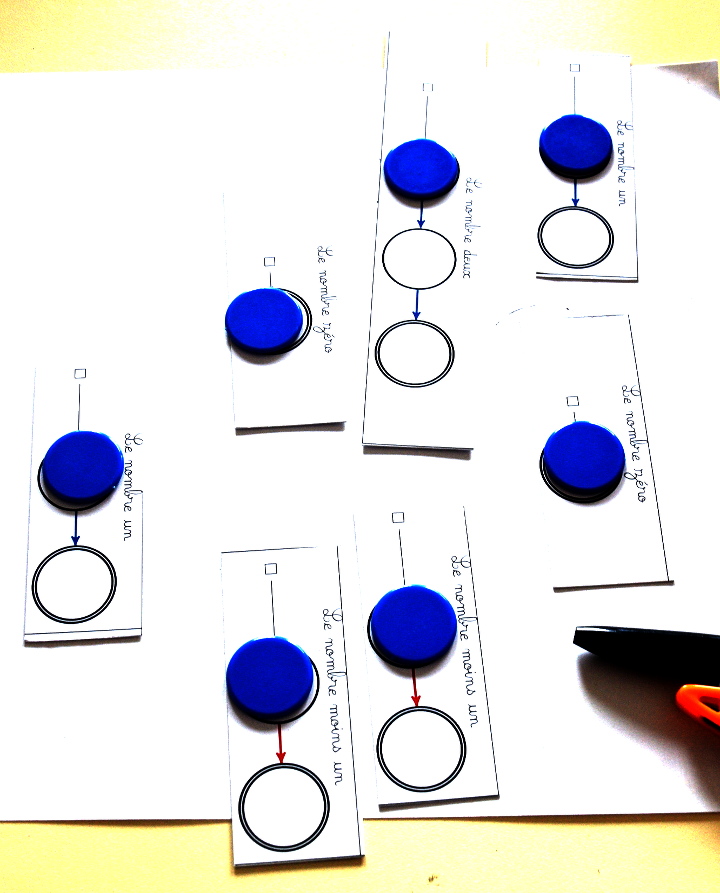
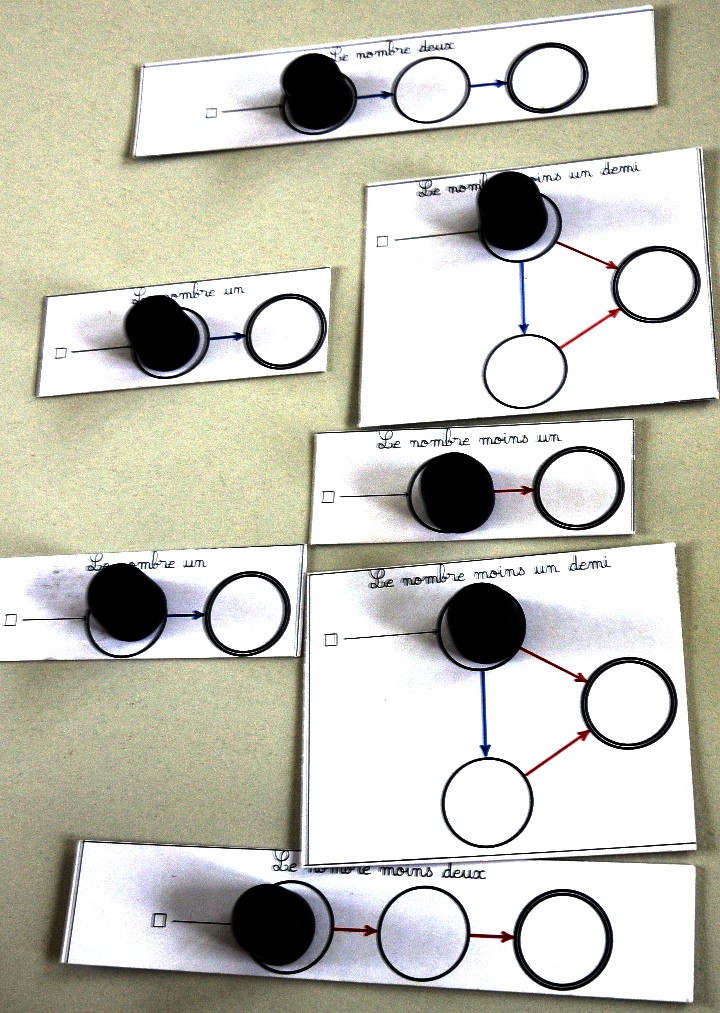
Durant la semaine des maths 2023 (thème : les mathématiques à la carte) des élèves de CP jusqu’à 3e ont pu jouer à la carte des cartes. En fait des élèves de GS ont pu jouer aussi, mais ils ont seulement dessiné des graphes, comme ceux-ci :
- une élève a inventé le jeu 0 contre -2 :
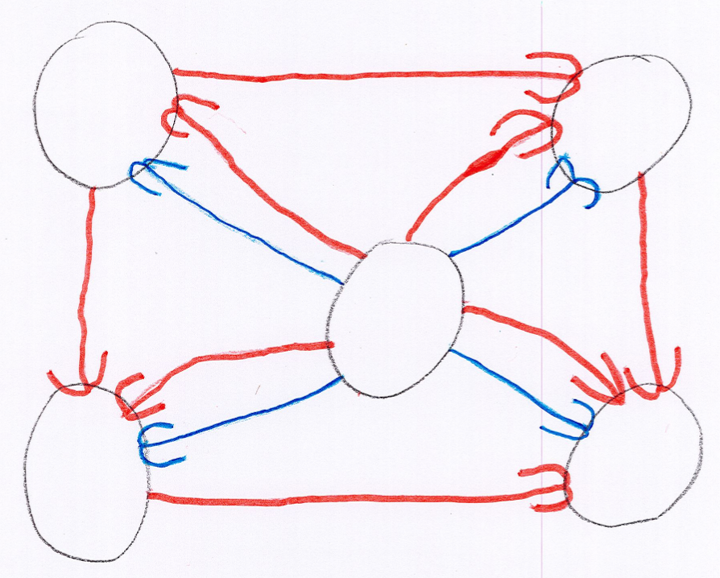
- une autre a réinventé le nombre 0 :
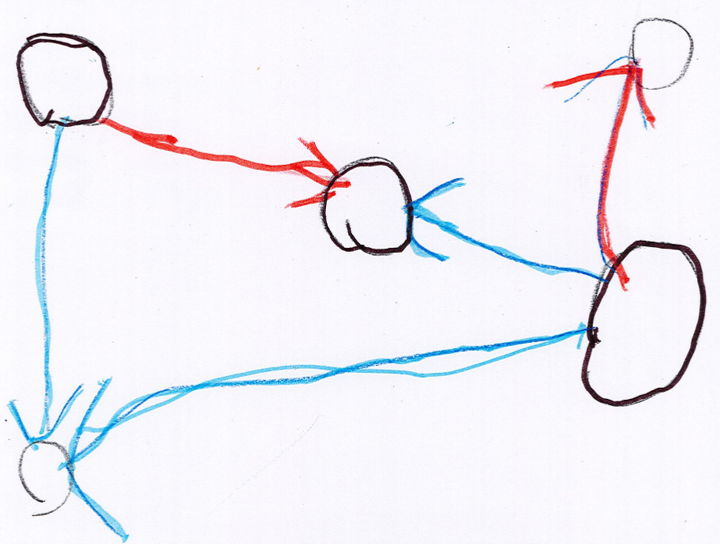
mais ici il s’agit d’une somme, dont les deux termes sont égaux à l’étoile (qui est son propre opposé donc la somme est nulle).
Le jeu de la carte des cartes par contre est propice à l’apprentissage des nombres entiers (relatifs !) parce que rapidement, en testant leurs jeux, les élèves comprennent que le jeu le plus équitable possible (quand on joue avec des nombres) est celui dans lequel le prochain qui joue est perdant. En cherchant à rendre leur jeu équitable, les joueurs vont donc instinctivement approcher la somme algébrique nulle, par un algorithme qui ne converge pas toujours (ajout de grandes cartes ou d’un grand nombre de cartes). Mais souvent, et dès le CP, on trouve des sommes nulles ou presques nulles qui sont estimées équitables par les joueurs.
CP
Un problème qui se pose à l’école maternelle lorsqu’on veut faire pratiquer des jeux à deux joueurs est l’émotivité de certains élèves, qui vivent comme un drame le fait de perdre au jeu. Ce phénomène est encore plus ou moins présent en CP.
On a commencé par jouer à des jeux sur 3 cartes (judicieusement choisies par l’animateur pour que la somme soit nulle -par exemple (+3)+(-2)+(-1) - afin que les joueurs sentent le caractère équitable du jeu).
Ensuite, il a été demandé aux joueurs de constituer (et tester) des jeux les plus équitables possibles. Une technique efficace a constitué à séparer les cartes gagnantes pour les bleus d’une part, et les cartes gagnantes pour les rouges d’autre part :
(côté positif : 2+1=3, côté négatif : -3-1=-4 : la somme est 3-4 qui est négative, donc le jeu n’est pas équitable)
Cette technique permet quand même souvent d’arriver à un jeu équitable :
(+2)+(+1)+(-1)+(-2)=0 :
&+2+1=4 et -1-3=-4 qui s’équilibrent :
Les élèves les plus hardis utilisent un grand nombre de cartes :
0+(+1)+(-1)+(-3)+(+1)+(+1)=-1 qui n’est donc pas équitable.
En jouant à ce jeu à condition de choisir la couleur rouge, on convainc aisément les élèves que le jeu est à l’avantage des rouges et on leur suggère de modifier le jeu pour le rendre plus équitable.
Certains élèves (à l’instar des collégiens, voir plus loin) accordent une grande importance à la disposition géométrique des cartes :
Le jeu est d’ailleurs équitable puisque (en partant de midi dans le sens des aiguilles d’une montre) (-2)+(+3)+(-2)+0+(+1)+0=0.
Durant toute la semaine des maths, du CP à la 3e, il a été observé une tendance à construire une seul graphe connexe par assemblage de cartes. Cela est dû à ce que, pour les élèves,
- tout graphe est connexe,
- on compte plutôt les sommets que les arêtes,
- il est possible de coller deux graphes en confondant l’arrivée du premier avec le départ du second (en tout cas avec les entiers).
Cette construction rappelle celle basée sur les catégories et foncteurs.
CE2
Comme les CP (onglet précédent), les CE2 jouent avec des entiers. Leur capacité à approcher rapidement une somme nulle est plus développée que chez les CP.
(0+1-1-3+1+1=-1, pour l’instant à l’avantage des rouges)
En remplaçant une des cartes 1 ci-dessus par une carte 2, on rétablit l’équilibre :
(0+1-1-3+2+1=0)
On constate l’usage fréquent (et pas seulement en CE2) de la carte zéro. Cela ne signifie pas que les élèves n’ont pas compris qu’elle ne sert à rien (ils le disent rapidement) mais elle permet de mettre beaucoup de cartes (donc faire un gros jeu, complexe) sans changer la valeur du jeu.
CM2
Là encore, l’approche de la somme nulle se fait assez instinctivement, mais les élèves de CM2 ayant déjà vu l’addition et la soustraction des décimaux, il est possible de justifier que leur jeu est, ou n’est pas, équitable.
Par exemple ce jeu est à l’avantage des rouges :
En effet (+2)+(+1)+(-0,5)+(-1)+(-2)=-0,5 qui est négatif, quoique faiblement : que les rouges disposent d’une stratégie gagnante n’est pas évident.
Avec les fractions, on trouve des manières astucieuses d’annuler la somme :
(+2)+(-1)+(+3)+(-3)+(-0,5)+(-0,5)=0 : le jeu est équitable.
(+2)+(+1)+(-0,5)+(-1)+(+1)+(-0,5)+(-2)=0 : là encore le jeu est équitable.
Les élèves aiment bien dessiner des motifs avec les cartes :
Ceci dit, la valeur est 0+(-0,5)+(-2)+(+2)+(-0,5)+(+1)+0=0 donc indépendamment de sa valeur esthétique, le jeu est équitable.
6e-5e
La semaine des maths s’est également déroulée en collège, et là aussi il a été possible de réifier des sommes algébriques. Les élèves de 5e n’ayant pas encore vu les entiers relatifs, n’ont pas tous pu suivre les explications par le calcul. Mais les plus créatifs ont apprécié la preuve mathématique que leur jeu est équitable (ou presque) par une addition de relatifs de surcroît menée mentalement !
Ce jeu, dans lequel le placement des cartes est soigné, n’est pas du tout équitable :
La somme 2,5-0,5+0+0,75+0,25+0,5-2+3 peut se calculer en commençant par enlever le nombre 0 puis en regroupant les cartes une par une :
- 2,5-0,5=2
- 2+0,75=2,75
- 2,75+0,25=3
- 3+0,5=3,5
- 3,5-2=1,5
- 1,5+3=4,5
Le résultat étant positif, on en déduit que le jeu est à l’avantage des bleus. On en déduit également une méthode pour améliorer le jeu : si on enlève la carte 2,5 le nouveau jeu vaut 4,5-2,5=2 et en rajoutant une carte -2 on équilibre le jeu.
Ce jeu non plus n’est pas équilibré :
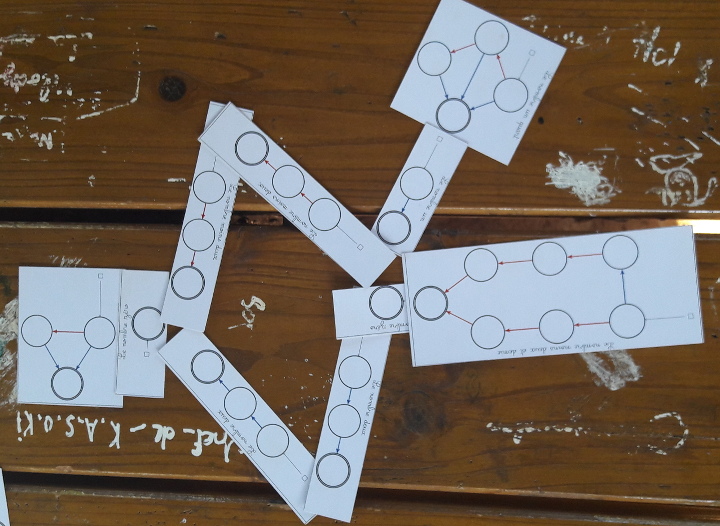
On constate que le losange du milieu s’additionne à 2+2-2-2=0 donc on peut ne pas le compter, ni les cartes 0. Il reste alors 0,5+1+0,75-2,5 :
- 0,5+1=1,5
- 1,5+0,75=2,25
- 2,25-2,5=-0,25
Le jeu est donc à l’avantage des rouges, quoique de suffisamment peu pour que cela ne saute pas aux yeux.
Ce jeu est encore moins équitable puisqu’il est à l’avantage des rouges :
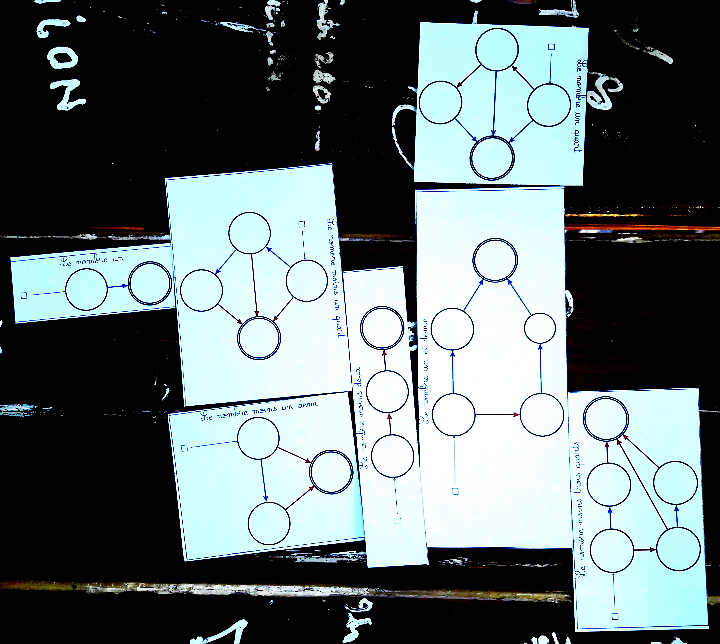
0,25+1-0,25-0,5+1,5-2-0,75=-0,75 : il suffirait d’enlever la carte -0,75 en bas à droite pour rendre le jeu équitable.
Ce jeu est presque équitable :
En effet la somme est 0,25+0,25+0,25+0,5-2+0,25+0,75-2,5+2=4×0,25+2-2+0,5-2,5+0,75=1-2+0,75=-0,25 qui est faiblement négatif : il suffirait de remplacer une des cartes 0,25 par une carte 0,5 pour annuler la somme.
Ce jeu est plus simple mais moins équitable (élève allophone en 6e) :
La somme des 4 termes est -2+1+0,25+0,25=-0,5 : si au lieu des cartes 0,25 on avait mis des cartes 0,5 le jeu aurait été équitable.
Noter que la stratégie gagnante pour les rouges n’est pas suffisamment évidente pour que le signe de ce jeu paraisse d’emblée négatif. La stratégie gagnante consiste à jouer d’abord sur une des cartes 0,25.
Ce jeu, n’utilisant pas un seul nombre entier, est également faiblement à l’avantage des rouges :
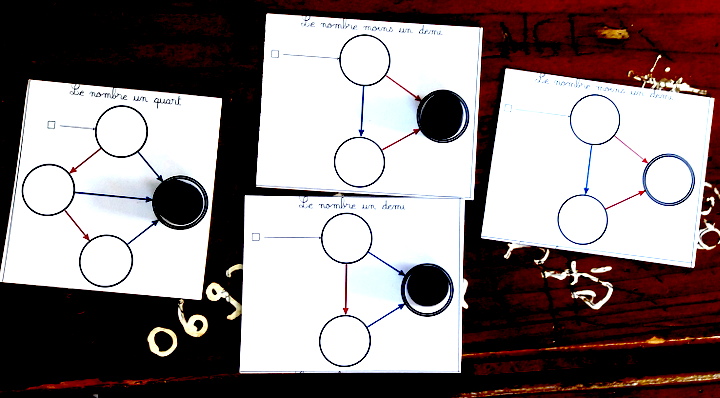
La somme vaut 0,25-0,5+0,5-0,5=-0,25 : en remplaçant une des cartes -0,5 par une carte -0,25 on équilibrait le jeu.
Ce jeu est encore plus à l’avantage des rouges :
En effet la somme vaut -2+1+0,25+0,25=-0,5. Peut-être les élèves (ULIS) voulaient-ils placer des cartes 0,5 au lieu des 0,25 : il est arrivé que des élèves, entendant que la table d’à côté avait produit un jeu équitable, cherchent à copier dessus, avec plus ou moins de bonheur, et de plaintes provenant de la table d’à côté...
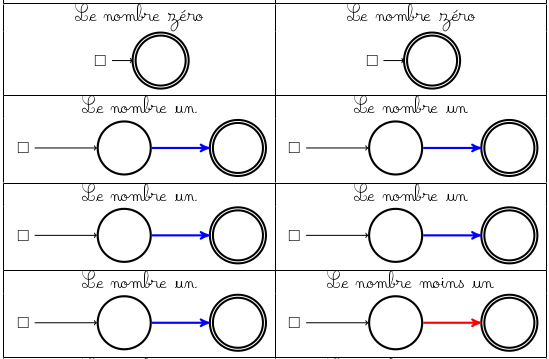
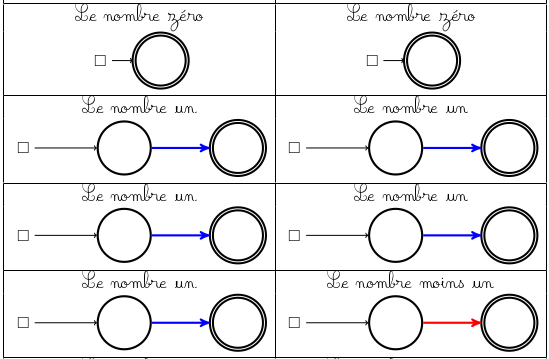
Ce jeu est particulièrement intéressant à étudier :
Les 4 termes valent respectivement -1, 1/4, 3/4 et 1/4. Or 1/4+3/4=1 qui neutralise le terme -1 et il reste 1/4=0,25 : le jeu est à l’avantage des bleus. Pour en convaincre son créateur, l’animateur demande à jouer les bleus, et joue d’abord dans la carte 3/4 (cela la transforme en 0,5 qui annule la somme).
Commentaire d’un des joueurs (CE 2) :
J’adore ce jeu parce qu’il est trop super génial !
Commentaires