Il y a au moins quatre manières de définir la valeur absolue :
- géométriquement, en tant que distance à l’origine ;
- comme fonction affine par morceaux ;
- comme composée des fonctions carré et racine ;
- algorithmiquement, par effaçage du bit de signe...
La seconde définition présente un intérêt du point de vue de l’enseignement basé sur algorithmique, parce qu’une fonction affine par morceaux est définie par tests et que ce genre de fonctions est une très bonne illustration de ce que font des tests. On coup d’œil sur la façon dont les valeurs absolues sont calculées dans JavaScript (code source de l’éditeur rhino qui se trouve dans ImageJ et dans CaRMetal) révèle que c’est bien par un test sur le signe de x que sa valeur absolue est définie :

On voit que la valeur absolue est définie pour x nul par 0, pour x positif par x, et sinon (pour x négatif) par -x. La question qui se pose alors est « où est l’algorithme là-dedans ? ». Deux problèmes peuvent être posés sur cette fonction définie par intervalles :
- représenter graphiquement la fonction (et conjecturer certaines propriétés sur le graphique) ; cet « algorithme » a peut-être déjà été vu en Seconde (exemple : AlgoBox).
- Comparer cette fonction aux autres versions de la valeur absolue.
Représentation graphique
Voici l’algorithme version AlgoBox :
Version AlgoBox de l'algorithme de tracé de la représentation graphique. À tester de préférence en mode pas-à-pas.
2 x EST_DU_TYPE NOMBRE
3 y EST_DU_TYPE NOMBRE
4 i EST_DU_TYPE NOMBRE
5 xx EST_DU_TYPE NOMBRE
6 yy EST_DU_TYPE NOMBRE
7 DEBUT_ALGORITHME
8 x PREND_LA_VALEUR -5
9 SI (x>0) ALORS
10 DEBUT_SI
11 y PREND_LA_VALEUR x
12 FIN_SI
13 SINON
14 DEBUT_SINON
15 y PREND_LA_VALEUR -x
16 FIN_SINON
17 POUR i ALLANT_DE -49 A 50
18 DEBUT_POUR
19 xx PREND_LA_VALEUR i/10
20 SI (xx>0) ALORS
21 DEBUT_SI
22 yy PREND_LA_VALEUR xx
23 FIN_SI
24 SINON
25 DEBUT_SINON
26 yy PREND_LA_VALEUR -xx
27 FIN_SINON
28 TRACER_SEGMENT (x,y)->(xx,yy)
29 x PREND_LA_VALEUR xx
30 y PREND_LA_VALEUR yy
31 FIN_POUR
32 FIN_ALGORITHME
Il est tout aussi possible de représenter directement la fonction, définie par un test, avec CaRMetal ou GeoGebra. Par exemple avec GeoGebra, on entre dans la fenêtre de saisie
f(x)=Si[x>0,x,-x]et on a la représentation graphique. Seulement dans ce cas on n’a pas utilisé d’algorithme, on a laissé GeoGebra le faire...
Distance à l’origine
La relative concision du langage JavaScript, et la possibilité qu’il offre de définir la fonction à part (en dehors de la boucle) :
function abs(x){
if(x>0){
return x;
} else {
return -x;
}
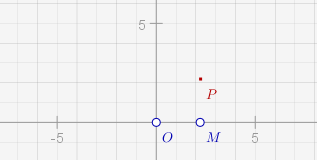
}donnent un intérêt certain à CaRMetal pour ce TP. Il en est de même pour le fait que c’est un logiciel de géométrie dynamique, ce qui permet facilement d’enchaîner sur la définition géométrique de la valeur absolue. Ci-dessous on a créé un point O de coordonnées (0,0) (donc fixe) et un point M sur l’axe des abscisses (il suffit de cliquer sur l’axe des x au moment de la création de M). Ensuite on a créé un point P dont l’abscisse est celle de M et dont l’ordonnée est la distance de O à M :
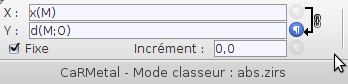
En activant la trace de P, on peut voir la représentation graphique (lieu des P) apparaître :

L’intérêt de cette activité est qu’on peut l’étendre à d’autres exercices, comme la somme ou la différence de plusieurs distances. Par exemple (après le cours sur la valeur absolue), on peut faire étudier la fonction d(A,M)+d(B,M)+d(C,M) où A, B et C sont trois points sur l’axe des abscisses : A(-3), B(1) et C(4).
La géométrie dynamique permet également (toujours a posteriori) de mieux faire le lien entre l’intervalle $[a-h ;a+h]$ et l’inéquation $|x-a|\leqslant h$, utile en analyse et en statistiques inférentielles.



Commentaires