Comme exemple de fonction, le fil directeur de cet article sera le sujet du bac STG CGRH Nouvelle-Calédonie novembre 2011 :
Un professionnel propose le stockage de photos anciennes sur des CD. Il peut produire au maximum 18 CD par jour et on note x le nombre de CD produits par jour.
Le coût journalier, exprimé en euros, pour un nombre entier x de CD produits est donné par f (x) où f est la fonction définie sur l’intervalle [0 ; 18] par
f (x) = x 2 + x + 15.
Définition
En Smalltalk, un bloc est entre crochets. Entre ces crochets il y a des instructions Smalltalk, dont la dernière (éventuellement, la seule) produit la valeur de sortie. Ces instructions sont séparées par un trait vertical des noms des antécédents, eux-mêmes précédés d’un double-point pour demander à Smalltalk de ne pas les évaluer. Dans l’exemple ci-dessus, la variable s’appelle x, et on la met devant le trait vertical sous la forme :x ; à la suite du trait vertical, on met l’expression de la fonction :
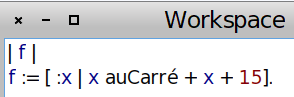
Cela se lit à voix haute comme « f est la fonction qui, à x, associe x au carré plus x plus 15 ».
La syntaxe est proche de la notation mathématique :
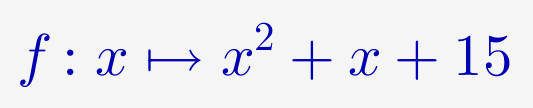
ou, si on préfère, de la notation Xcas :

Retour au sujet du bac STG :
Quel est le coût fixe journalier ? Quel est le coût journalier pour 10 CD produits ?
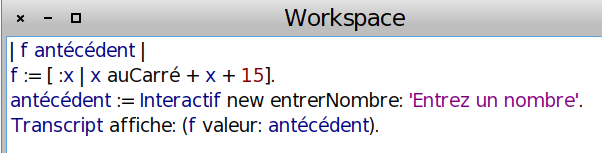
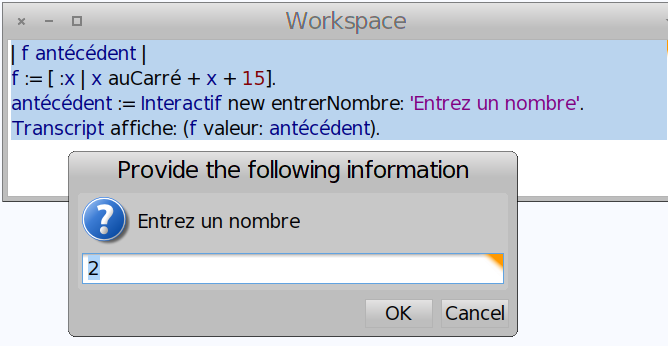
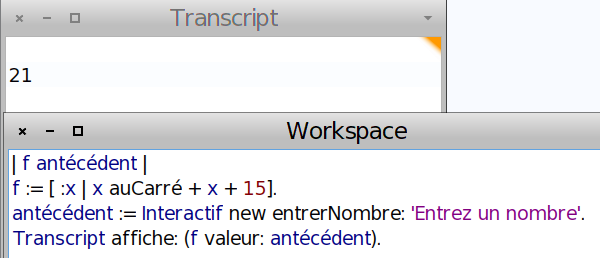
Pour obtenir l’image d’un nombre par f, on fait juste f valeur: x :
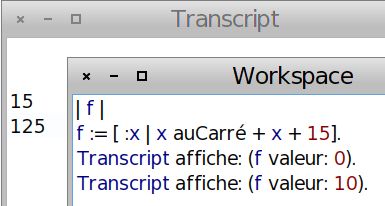
Graphique
Suite du sujet de bac :
Recopier et compléter le tableau de valeurs ci-dessous :
x 0 2 4 6 8 10 12 14 16 18 ƒ(x) 35
C’est là que l’aspect « objet » des fonctions donne toute sa saveur : À l’instar d’un ribosome qui parcourt une chaîne et transforme l’un après l’autre ses éléments pour fabriquer progressivement une protéine, une fonction Smalltalk peut picorer [1] les nombres d’un tableau, obtenant ainsi un autre tableau. Le tableau des valeurs de x est un intervalle de pas 2 :
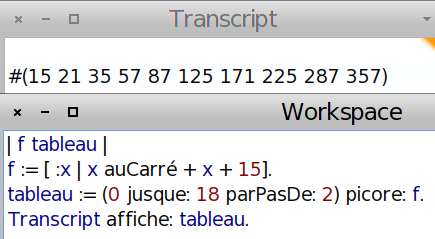
Mais f peut également picorer des tableaux faits sur mesure ou des ensembles, etc. Une application est la construction par MathOntologie d’une collection de points donnant l’allure de la représentation graphique :
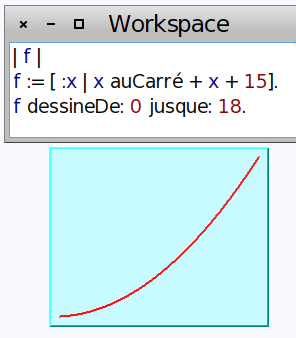
Variations
Suite du sujet de bac :
Tous les CD produits sont vendus au prix unitaire de 17 euros.
1.a. Soit R(x) la recette journalière, en euros, pour la vente journalière de x
CD.Exprimer R(x) en fonction de x.
MathsOntologie ne fait pas de calcul formel mais permet de définir R(x) comme un bloc :

Ensuite, l’expression du bénéfice B(x) peut être vérifiée non pas en soustrayant deux blocs f et R (on ne peut pas soustraire de blocs) mais en définissant un nouveau bloc B par
B := [ :x | R valeur: x - ( f valeur: x ) ].
On peut le représenter graphiquement ce qui donne une idée de ses variations et donc du nombre de valeurs qui annulent B(x) :

Déterminer graphiquement le nombre de CD qui doivent être vendus
pour réaliser un bénéfice. Conclure par une phrase.
On voit graphiquement que les nombres cherchés constituent un intervalle ; ses bornes peuvent être déterminées numériquement par :
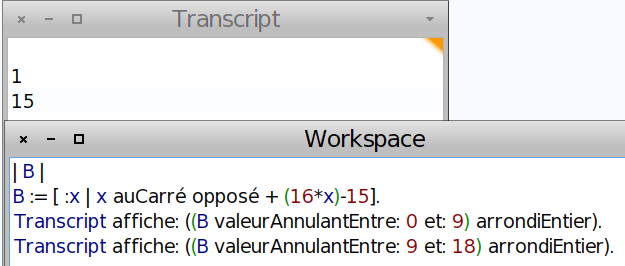
La première solution a été cherchée entre 0 et 9 et la seconde, entre 9 et 18.
Estimer en expliquant la démarche suivie, le nombre de CD donnant un
bénéfice maximal.

c. Étudier les variations de la fonction B.
d. En déduire alors la valeur de x pour laquelle le bénéfice maximal est atteint.
Ce résultat confirme-t-il l’estimation de la question 1. d. ?
La fonction B’ peut être évaluée numériquement : C’est la fonction qui, à x, associe la dérivée de B en x ; il suffit alors de chercher où elle s’annule :
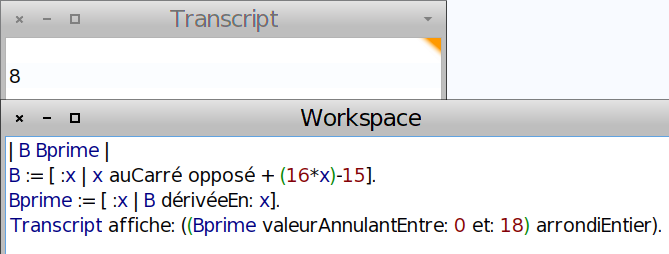
Calculer ce bénéfice maximal.
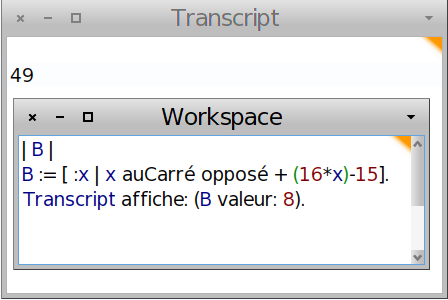
booléens
Si la valeur retournée par un bloc est booléenne, la description du bloc ressemble beaucoup [2] à celle d’un ensemble par compréhension.
Par exemple, l’ensemble des diviseurs premiers de 24 s’écrit comme ceci [3] :

La version Smalltalk (dp comme « diviseurs premiers » y ressemble beaucoup :
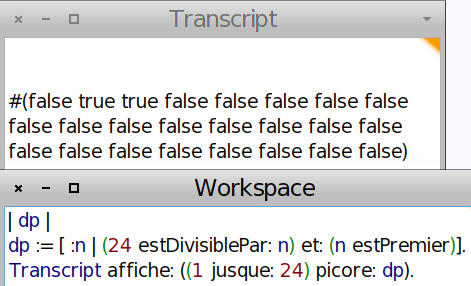
Le tableau renvoyé est la fonction indicatrice de l’ensemble.
algorithmes
Une fonction peut aussi être définie par algorithme ; par exemple, la fonction f définie par l’algorithme de Heron ci-dessous :
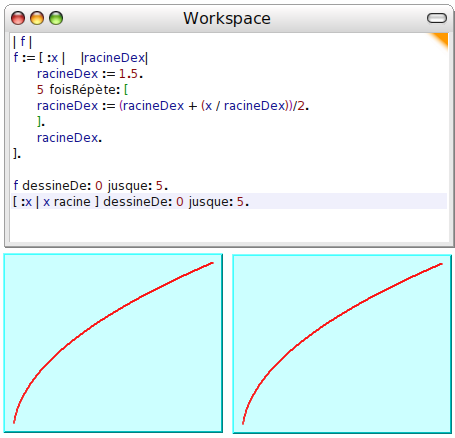
Ici la variable locale s’appelle racineDex (« racine de x ») et est retournée par la fonction à la fin (après le bloc vert). Elle est initialisée à 1,5 puis une boucle est effectuée 5 fois, dans laquelle racineDex est remplacé par la moyenne entre lui-même et le quotient de x par lui.
Les deux représentations graphiques sont indiscernables l’une de l’autre, ce qui illustre la précision de l’algorithme. En plus, la fonction f peut être dérivée numériquement, on peut chercher ses extrema sur un intervalle etc. Et en remplaçant 5 par 5 commeComplexe, on peut s’en servir pour calculer des racines de nombres négatifs...
Un autre exemple de fonction définie par un algorithme (ici, une somme) est la fonction de Riemann, précurseur de la fonction de Weiertrass (elle n’est dérivable presque nulle part) :
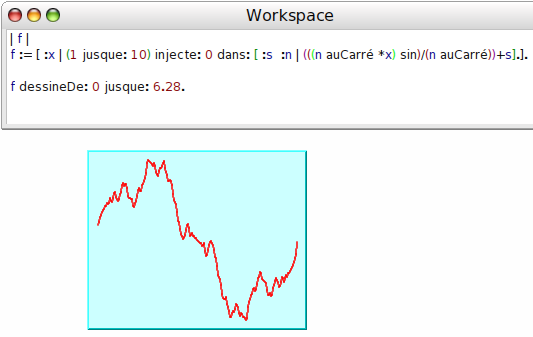
Le bloc à l’intérieur n’est pas picoré mais injecté : Il a deux variables dont la première sert d’accumulateur. Il prend donc pour valeur finale la somme des sinus de n au carré fois x, divisés par le carré de n, pour n allant de 1 à 10.
Une fois définie, cette fonction peut être représentée graphiquement, voire intégrée numériquement, avec suffisamment de précision pour voir que l’intégrale de 0 à π vaut 2 :

Et que l’intégrale de 0 à 2π vaut 0 :
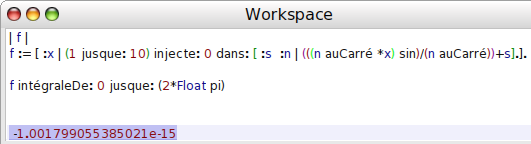
Pour avoir les affichages ci-dessus, le transcript n’a pas été utilisé, mais le script a été imprimé plutôt qu’exécuté : Là encore, la dernière expression est celle qui est envoyée à print.


Commentaires