Problème 1 : Points proches dans le plan
Points
pyplot
Le sujet adopte l’approche de pyplot :
Le nuage de points est représenté par
- une liste d’abscisses
coords_x - une liste d’ordonnées
coords_y
Ainsi les coordonnées du point Mi sont
coords_x[i]
coords_y[i]Pour dessiner les points il suffira donc, sous pyplot, de faire
from matplotlib.pyplot import *
plot(coords_x,coords_y)
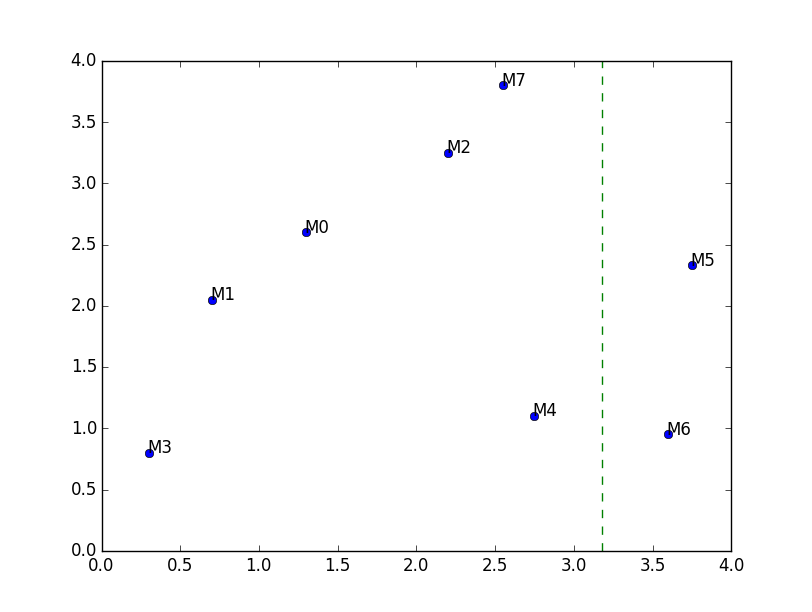
show()Avec ces coordonnées
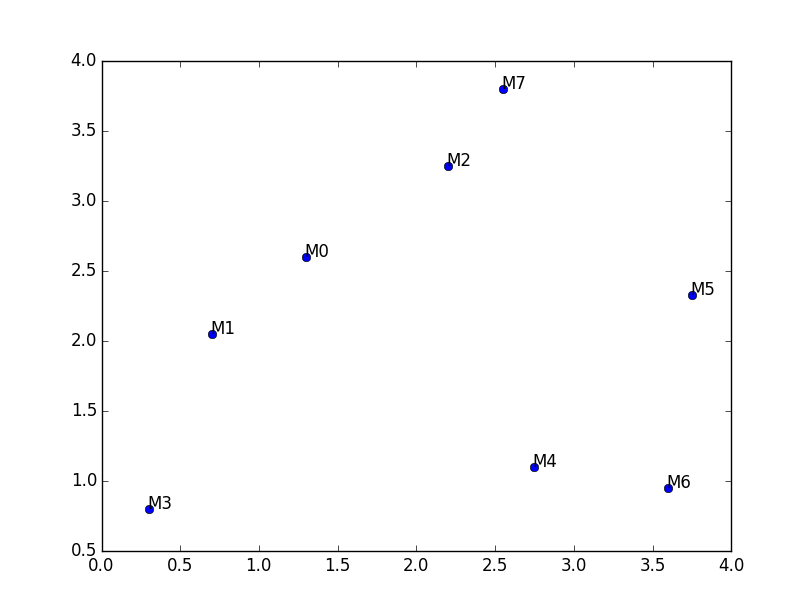
coords_x = [1.3,0.7,2.2,0.3,2.75,3.75,3.6,2.55]
coords_y = [2.6,2.05,3.25,0.8,1.1,2.33,0.95,3.8]on a le nuage de points de l’énoncé :
On suppose qu’on a une variable globale
n = len(coords_x)
Approche exhaustive
Question 1
from math import sqrt
def distance(i, j):
xi, yi = coords_x[i], coords_y[i]
xj, yj = coords_x[j], coords_y[j]
return sqrt((xj - xi)**2 + (yj - yi)**2)Remarque : quitte à utiliser une fonction du module math, on aurait pu faire plus simple avec la fonction hypot qui fait la moitié du travail. Cela aurait donné
from math import hypot
def distance(i, j):
return hypot(coords_x[i]-coords_x[j], coords_y[i]-coords_y[j])Question 2
Les flottants [1] sont stockés sous la forme 1,... × 2n dite à virgule flottante. Avec la norme IEEE 754 qui, en simple précision (32 bits) réserve 1 bit pour le signe, 8 pour l’exposant (le n) et 23 pour la mantisse (les points de suspension).
Dans cette écriture, n’existent que les décimaux qui ont un développement dyadique. Les autres sont donc approximés par les premiers. Pour la fonction distance cela peut donc signifier un calcul non exact. Concrètement, on évitera de comparer 2 distances avec ==
Question 3
Il s’agit ici de parcourir intelligemment les listes de points (leurs indices en fait) et de calculer la distance qui les sépare 2 à 2... et de mémoriser la plus petite. Intelligemment signifie qu’on ne va pas calculer 2 fois la même distance pour le couple (i, j) puis pour le couple (j, i) :
def plus_proche():
proche_i, proche_j = None, None
min_dist = float('inf')
for i in range(n-1):
for j in range(i+1, n):
d = distance(i, j)
if d < min_dist:
min_dist = d
proche_i, proche_j = i, j
return proche_i, proche_jQuestion 4
On va comparer :
M0 à M1… Mn-1 soit n−1 comparaisons, puis
M1 à M2…Mn-1 soit n−2 comparaisons, puis
etc.
Mn−2 à Mn-1 soit 1 comparaison.
Au total le nombre de comparaisons est le n-ème nombre triangulaire : la fonction plus_proche est donc en O(n2) .
Tri
Question 5
Voici la fonction de tri donnée :
def tri(liste):
n = len(liste)
for i in range(n):
pos = i
while pos > 0 and liste[pos] < liste[pos-1]:
liste[pos], liste[pos-1] = liste[pos-1], liste[pos]
pos -= 1Cette fonction ne retourne rien (ou plutôt None) mais trie en place le tableau qu’on lui passe. La méthode est la suivante : on parcourt les éléments depuis l’indice 0 par une boucle for et à chaque passage on va placer l’élément courant (indice i) à sa place parmi les éléments à gauche de lui (indices 0 à i-1). Il s’agit donc d’un tri par insertion.
L’invariant est donc : à la sortie de la boucle for le tableau est divisé en deux parties : de 0 à i les éléments sont triés par ordre croissant, et le reste pas trié.
Pour i=0 la proposition est trivialement vraie.
Supposons la propriété est vraie pour un i, voyons avec i+1. Appelons e la valeur l[i+1]. On a trois cas pour le passage du while et donc la sortie du for :
- on n’entre pas dans le
while: pos vaut alors i+1 et donc l[i+1] ≥ l[i] notre tableau est alors l[0] ≤ ... ≤ l[i] ≤ l[i+1] la proposition est vraie ; - on entre dans le
whileet on en sort parce quepos > 0est faux alors on a : e en première position soit e < l[0] ≤ ... ≤ l[i] là encore la proposition est vraie - on entre dans le
whileet on en sort parce que liste[pos] &ge liste[pos-1] c’est-à-dire qu’on a : l[pos-1] ≤ e < l[pos+1] là encore on a un tableau qui reste trié (e est bien placé) et qui a un élément de plus : la proposition est vraie.
Question 6
Raisonnons dans le pire des cas et comptons le nombre de passages dans la boucle while :
Pour i=0 on ne passe pas dans le while
Pour i=1 on passe 1 fois
Pour i=2 on passera 2 fois, poussant liste[pos] en position 0
etc.
Pour i=n−1 on passera là encore n−1 fois au plus.
Au total on a donc n(n−1) sur 2 passages : la fonction tri est en O(n2) .
Question 7
Il faudrait changer le test dans le while :
coords_x[liste[pos]] < coords_x[liste[pos-1]]Du coup, pour ne pas faire deux fonctions (une pour les x l’autre pour les y) on peut ajouter un paramètre à la fonction de tri :
def tri(liste, coords):
n = len(liste)
for i in range(n):
pos = i
while pos > 0 and coords[liste[pos]] < coords[liste[pos-1]]:
liste[pos], liste[pos-1] = liste[pos-1], liste[pos]
pos -= 1Ainsi on pourra trier nos points par abscisses croissantes :
pos_x = list(range(n))
tri(pos_x, coords_x)ou par ordonnées croissantes :
pos_y = list(range(n))
tri(pos_y, coords_y)Question 8
Le tri fusion (ou mergesort) de complexité O(n×log(n)) est meilleur.
Clusters
Dans la suite, un sous-ensemble de points est appelé un cluster. Par exemple, le nuage de points de l’énoncé devient le cluster suivant :
liste_x = [3,1,0,2,7,4,6,5]
liste_y = [3,6,4,1,5,0,2,7]
cluster_a = [[liste_x, liste_y]]Alors que les points à gauche de la ligne verte pointillée forment le cluster
cluster_b = [ [3,1,0,2,7,4],
[3,4,1,0,2,7] ]Question 9
Il s’agit de parcourir les indices des abscisses et des ordonnées et de garder ceux dont le point M correspondant vérifie xmin ≤ coords_x[i] ≤ xmax
def sous_cluster(cl, x_min, x_max):
sscl = [[], []]
for i in cl[0]:
if x_min <= coords_x[i] <= x_max:
sscl[0].append(i)
for i in cl[1]:
if x_min <= coords_x[i] <= x_max:
sscl[1].append(i)
return ssclQuestion 10
def mediane(cl):
n = len(cl[0])
if n%2 == 0:
return coords_x[cl[0][n//2]]
else:
i1 = cl[0][(n-1)//2]
i2 = cl[0][n//2]
return (coords_x[i1] + coords_x[i2]) / 2Récursivité
principe de l’algorithme
On applique la méthode « diviser pour régner » :
- Si le cluster contient 2 ou 3 points, on calcule toutes les distances possibles :
- S’il n’y a qu deux points, il n’y a qu’une seule distance.
- S’il y a trois points, ils forment un triangle et la distance voulue est le plus petit côté de ce triangle.
- Sinon, on sépare le cluster en deux sous-clusters de taille moitié suivant la médiane des abscisses (ci-dessus en trait rouge).
- Les deux points les plus proches sont tous les deux à gauche du trait rouge, tous les deux à droite du trait rouge, ou de part et d’autre du trait rouge.
- On calcule récursivement le couple le plus proche à gauche, et le couple le plus proche à droite. On note d0 la plus petite distance obtenue (en vert à gauche ci-dessous).
- On cherche s’il existe une paire de points (M1,M2) telle que M1 est à gauche du trait rouge, M2 est à droite du trait rouge et d(M1,M2)<d0.
- Si on en trouve un (ou plusieurs), on renvoie la plus petite de ces distances. Sinon on renvoie d0.
Les algorithmes de cette partie sont de Serge Bays.
Question 11
def gauche(cl):
med = (len(cl[0])+1) // 2
clg0 = []
for i in range(med):
clg0.append(cl[0][i])
clg1 = list(clg0)
tri(clg1,coords_y)
return [clg0, clg1]droite
La fonction droite dont on aura également besoin plus loin, est
def droite(cl):
med = (len(cl[0])+1) // 2
cld0= []
for i in range(med, len(cl[0])):
cld0.append(cl[0][i])
cld1 = list(cld0)
tri(cld1,coords_y)
return [cld0, cld1]Question 12
M1 est à gauche de la ligne rouge, donc si M2 est en dehors de la bande verte, M2 est à droite de la seconde ligne verte : la différence entre les abscisses des deux points est supérieure à d0 et il en sera de même, a fortiori, pour la distance d(M1,M2).
De même, comme M2 est à droite de la ligne verte, il est inutile de chercher M1 à gauche de la ligne verte de gauche, car là encore d(M1,M2) serait supérieur à d0.
Question 13
Avec la fonction sous_cluster de la question 9, la bande centrale se calcule en quelques lignes de ode, et en O(n) :
def bande_centrale(cl, d0):
x0 = mediane(cl)
return sous_cluster(cl, x0-d0, x0+d0)Question 14
On considère le point dont l’abscisse est la médiane des abscisses (il est sur le trait rouge) et dont l’ordonnée est la moyenne des ordonnées de M1 et M2. On considère le rectangle centré sur ce point, de largeur 2×d0 et de hauteur d0 (ce rectangle contient donc M1 et M2). Si ce rectangle contenait plus de 8 points, deux d’entre eux seraient nécessairement du même côté de la ligne rouge, et à distance inférieure à d0. Ce qui est contraire à la définition de d0.

Donc il y a au maximum, dans le sens des ordonnées croissantes, 6 points entre M1 et M2 dans la bande verte (les 8 points maximum en question, moins M1 et M2).
Question 15
def fusion(cl, d0):
for ind in cl[0]:
j = 0
while cl[1][j] != ind:
j = j + 1
k = j + 1
while k < len(cl[1]) and k < j + 8:
d = distance(ind, cl[1][k])
if d < d0:
d0 = d
k = k + 1
return d0Question 16
def distance_minimale(cl):
if len(cl[0]) <= 3:
d = distance(cl[0][0], cl[0][1])
if len(cl[0]) == 3:
d2 = distance(cl[0][0], cl[0][2])
if d2 < d:
d = d2
d3 = distance(cl[0][1], cl[0][2])
if d3 < d:
d = d3
return d
else:
x0 = mediane(cl)
cg = gauche(cl)
cd = droite(cl)
d0 = distance_minimale(cg)
dd0 = distance_minimale(cd)
if dd0 < d0:
d0 = dd0
bc = bande_centrale(cl, d0)
return fusion(bc, d0)Question 17
Pour trouver les points les plus proches (et la distance minimale) du cluster de taille n, on
- cherche la distance minimale dans le cluster de gauche, ce qui prend C(n//2) opérations élémentaires,
- cherche également la distance minimale dans le cluster de droite, ce qui prend aussi C(n//2) opérations élémentaires,
- choisit la distance d0 la plus petite parmi celles qu’on vient de calculer récursivement (temps constant),
- calcule la bande centrale, en O(n) d’après la question 13,
- fusionne avec la bande de largeur d0 autour de la médiane, en O(n) d’après la question 15.
Le tout est donc en C(n//2)+C(n//2)+O(n)+O(n)=C(n//2)+O(n) cqfd.
Question 18
On en déduit par récurrence que C(n)=O(n×log(n)). Par exemple en ne regardant que les puissances de 2, on a n=2p et on raisonne par récurrence sur p pour montrer que C(2p)≤k×p×2p :
- si p=1, C(2)=1 alors que 2×log2(2)=2.
- si C(2p-1)≤k(p-1)×2p-1 alors C(2p)≤2×C(2p-1)+K×2p≤2×k(p-1)×2p-1+K×2p=k×p×2p+(K×2p-k×2p)≤k×p×2p si on a choisi k≥k cqfd
Problème 2 : Composantes connexes et biconnexes
Graphes
Voici les graphes de l’énoncé, au format Nirina974 :
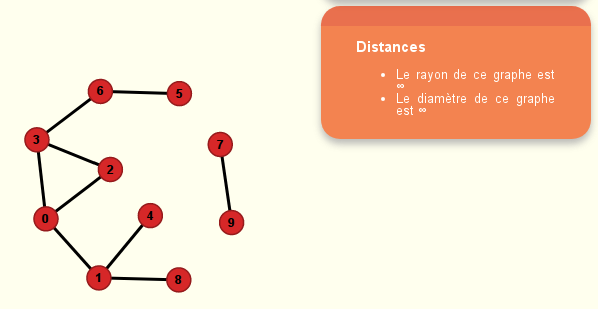
Gex :
(on voit qu’il n’est pas connexe puisque tous ses sommets sont d’excentricité infinie)
G’ex :
Celui-là par contre est connexe. Mais on verra qu’il n’est pas biconnexe.
BDD
Question 19
Internet est un réseau international permettant à deux machines numériques, même distantes, de communiquer entre elles (par TCP/IP par exemple). Alors que le World Wide Web est un système de navigation dans de l’hypertexte.
Par exemple les réseaux P2P, les courriels, les visioconférences utilisent Internet mais pas le web.
Question 20
Le RGPD demande, entre autres, que
- lors de la création du compte, chaque utilisateur soit informé de l’utilisation des données qu’il postera sur le site.
- les identifiants des usagers ne soient pas diffusés en dehors du site sans autorisation expresse.
Question 21
Pour connaître le nombre total de ressources de type cours présentes sur le site on peut faire
select count(*) from ressources where type='cours';Question 22
La requête
select ressources.titre, comptes.nom
from chargement
join ressources on ressources.id=chargement.id_r
join comptes on comptes.id=chargement.id_u
order by chargement.date DESC LIMIT 1;renvoie
Machine à décalage|Alan Turing
Plus généralement, elle renvoie le (DESC) plus récent (LIMIT 1) couple formé d’un titre (de ressource) et du nom de celui qui l’a chargé, autrement dit : la dernière ressource chargée et le nom de celui qui l’a chargée.
Les corrigés suivants sont de Rafael Lopez, d’Orsay.
Question 23
SELECT ch.id_u AS x, r.owner AS y, COUNT(*) AS n
FROM ressources r
INNER JOIN chargement ch ON ch.id_r = r.id
GROUP BY ch.id_u, r.owner;On peut même en faire une « fonction » :
WITH Q23(r1,r2,r3) AS
(SELECT ch.id_u AS x, r.owner AS y, COUNT(*) AS n
FROM ressources r
INNER JOIN chargement ch ON ch.id_r = r.id
GROUP BY ch.id_u, r.owner
)Question 24
Avec la question précédente :
SELECT r1 as id1, r2 as id2
FROM Q23
WHERE id1 IN (SELECT r2 FROM Q23 WHERE r1 = id2)
AND id2 IN (SELECT r1 FROM Q23 WHERE r2 = id1);connexes
Question 25
avec la représentation
g_ex_a = [
(0,1), (0,2), (0,3), (1,0), (1,4), (1,8),
(2,0), (2,3), (3,0), (3,2), (3,6),
(4,1), (5,6), (6,3), (6,5),
(7,9), (8,1), (9,7)
]la fonction
def adjacences(n,li):
la = []
for i in range(n):
la.append([])
for couple in li:
if couple[0]==i:
la[i].append(couple[1])
return lacrée
g_ex_b = [[1, 2, 3], [0, 4, 8], [0, 3],
[0, 2, 6], [1], [6], [3, 5], [9], [1], [7]
]parcours
La classe Arbre est définie ainsi :
class Arbre():
def __init__(self,sommet):
self.sommet = sommet
self.children = []
def add_child(self,child):
self.children.append(child)et le parcours :
def parcours(listes_adjacences):
n = len(listes_adjacences)
deja_vu = [False] * n
def explorer(i):
arbre = Arbre(i)
voisins = listes_adjacences[i]
for s in voisins:
if not deja_vu[s]:
deja_vu[s] = True
arbre.add_child(explorer(s))
return arbre
res = []
for i in range(n):
if not deja_vu[i]:
deja_vu[i] = True
res.append(explorer(i))
return resQuestion 26
Le parcours renvoie une liste d’arbres (c’est-à-dire d’objets de la classe Arbre). Une telle liste modélise une forêt. Le parcours est un parcours en profondeur. Il construit la forêt couvrante que voici :
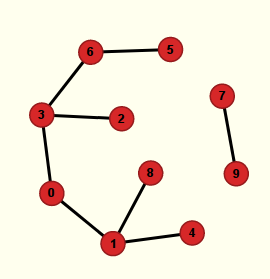
Cette forêt n’est pas connexe, mais chacune de ses composantes connexes est un arbre. Le plus petit de ces arbres est ⑦-⑨ et tout le reste forme cet arbre :
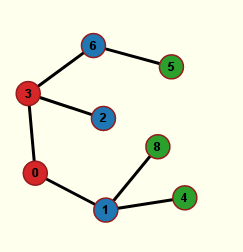
Question 27
- La fonction démarre par un appel à la fonction
lenqui, en général, est en O(|V|) mais en Python elle est en O(1). - Idem pour la constitution de la liste
deja_vuqui est en O(|V|). - Dans la fonction
explorer, on boucle sur les voisins d’un sommet. La fonction est donc en O(|E|) - La boucle principale est en O(|V|) et dans cette boucle, pour chaque sommet, on boucle sur se voisins. Au total on parcourt 2 fois chaque arête et la boucle principale est en O(|E|)
La fonction parcours est donc en O(|V|)+O(|V|)+O(|E|)=O(|V|)+O(|E|)=O(|V|+|E|) cqfd.
Question 28
Un graphe est connexe si, pour tous sommets x et y du graphe, il existe un chemin joignant x à y.
Alternativement, avec le vocabulaire de SNT, un graphe est connexe si son diamètre est fini.
Question 29
Un graphe est connexe si et seulement si le nombre de ses composantes connexes est 1. Or pour chacune d’entre elles, la fonction parcours renvoie une liste des arbres couvrants, à raison d’un arbre par composante connexe. Il suffit donc, à l’instar d’un sylviculteur, de compter les arbres de la forêt pour avoir le nombe de composantes connexes du graphe. La connexité du graphe est caractérisée par l’égalité entre ce nombre, et 1 :
def connexe(listes_adjacences):
return len(parcours(listes_adjacences))==1Question 30
On commence par créer une fonction auxiliaire, qui à un arbre p_graphe, associe la liste de ses sommets :
def liste_sommets(arbre):
liste = [arbre.sommet]
for s in arbre.children:
liste += liste_sommets(s)
return listeLa fonction
def composantes_connexes(p_graphe):
return [liste_sommets(c) for c in p_graphe]renvoie les composantes connexes du graphe, sous forme de listes de sommets.
Avec
composantes_connexes(parcours(g_ex_b))
on obtient cette description des deux composantes connexes :
[[0, 1, 4, 8, 2, 3, 6, 5], [7, 9]]
Question 31
La profondeur de récursion (hauteur de la pile des appels) est la hauteur de l’arbre couvrant construit par la fonction parcours. La fonction parcours ne peut donc pas être appliquée à un graphe trop allongé. Si le nombre de sommets est élevé il faudra augmenter la taille de la pile d’appels ou adopter un algorithme itératif.
biconnexes
Pour Internet, les graphes biconnexes sont intéressants parce qu’une panne d’un seul routeur ne suffit pas à empêcher le réseau de fonctionner.

Question 32
Si un graphe est biconnexe, alors pour tous sommets x et y, il existe un cycle comprenant x et y. Ce cycle comprend lui-même deux chemins, joignant x et y. A fortiori il y a (au moins) un chemin allant de x à y : le graphe est connexe.
Question 33
Le graphe de l’énoncé est connexe mais pas biconnexe (voir question 34 ci-après), et répond donc à la question. Un exemple plus simple est le graphe ⓪-①-② qui est connexe (rayon 1, diamètre 2, centre ①) mais ne comprend aucun cycle, donc ⓪ et ① ne sont dans aucun cycle propre.
Question 34
Avec Nirina974 il est aisé de voir quels sont les points d’articulation du graphe : il suffit d’enlever (puis remettre) l’un après l’autre les sommets et regarder si le graphe est encore connexe, ou pas (cela se voit à la couleur, uniformément rouge si le graphe n’est plus connexe). Les points d’articulation sont donc
- le sommet 4 :
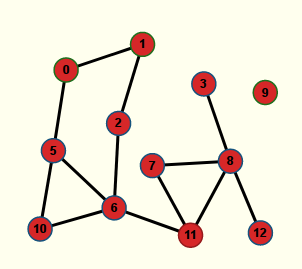
- le sommet 6 :

- le sommet 8 :
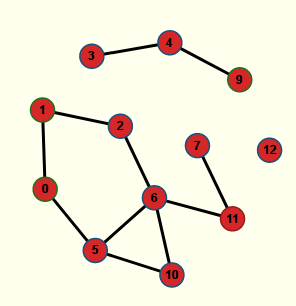
- le sommet 11 :
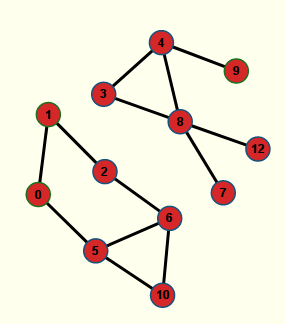
G’ex possède donc 4 points d’articulation. On en déduira par la suite, qu’il n’est pas biconnexe.
Question 35
Supposons que le graphe G possède un point d’articulation a. Alors il existe deux sommets x et y tels que tout chemin de x à y passe par a. Il ne peut donc pas exister de cycle contenant x et y et G n’est pas biconnexe.
Question 36
- Si G n’a pas de point d’articulation, alors G est connexe et il existe une chaîne joignant x à y.
- S’il n’existait aucun cycle élémentaire contenant x0 et x1 alors x0 serait un point d’articulation.
- Supposons qu’il existe un cycle élémentaire contenant x0 et xi, et que ce cycle ne passe pas par xi+1 (sinon on aurait fini). Alors il existe un autre cycle passant par x0 et xi+1 (sinon x1 serait un point d’articulation).
- Par récurrence sur i, on en déduit qu’il existe un cycle élémentaire passant par x et y : G est biconnexe.
Question 37
On effectue un parcours en profondeur, à partir du sommet à tester. Cela construit un arbre couvrant de G. Le sommet de départ est d’articulation si et seulement si plusieurs branches de l’arbre en partent.
Question 38
On boucle sur les |V| sommets du graphe. Pour chacun d’entre eux, on effectue un parcours en profondeur - en O(|V|+|E|) - pour construire un arbre couvrant, puis on compte les branches de l’arbre issues du sommet courant. S’il y a plus d’une branche, l’algorithme s’arrête sur la réponse non (le graphe n’est pas biconnexe). Sinon on continue à boucler, et si à la fin - en O(|V|²+|E|×|V|) - tous les arbres couvrants sont à un seul tronc, le graphe est biconnexe.
algorithme
parcours
Voixi le script de l’énoncé, avec calcul du préfixe :
def parcours(listes_adjacences):
n = len(listes_adjacences)
deja_vu = [False] * n
prefixe = [-1] * n
count = 1
def explorer(i):
nonlocal count
prefixe[i] = count
count += 1
arbre = Arbre(i)
voisins = listes_adjacences[i]
for s in voisins:
if not deja_vu[s]:
deja_vu[s] = True
arbre.add_child(explorer(s))
return arbre
deja_vu[0] = True
return explorer(0), prefixeQuestion 39
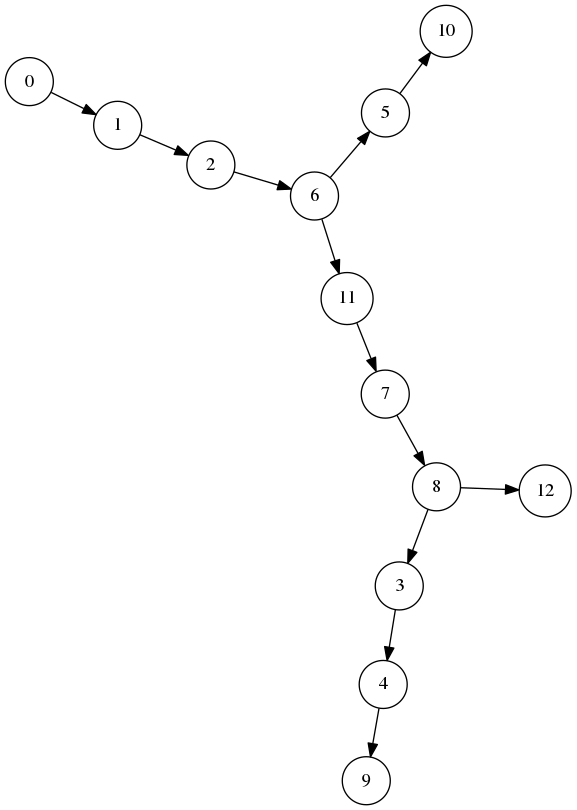
Le parcours du graphe à partir de ⓪ donne l’arbre couvrant suivant :
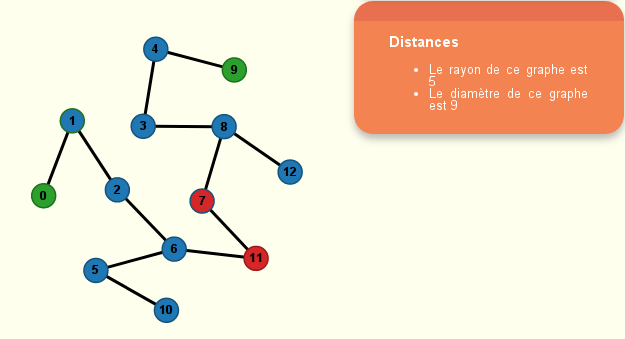
et la liste prefixe suivante :
[1, 2, 3, 10, 11, 5, 4, 8, 9, 12, 6, 7, 13]
Ce qui correspond à ces préfixes :
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | 2 | 3 | 10 | 11 | 5 | 4 | 8 | 9 | 12 | 6 | 7 | 13 |
Question 40
Si
prefixe[i] < prefixe[j]
cela signifie que j a été placé dans l’arbre couvrant, plus tard que i. Donc j est plus « haut » que i dans l’arbre : j est un descendant de i cqfd.
Question 41
Pour rappel, voici le graphe :

et ses ord (prefixe minimal parmi les voisins des descendants) :

On constate que
- 9, qui est le fils de 4, est d’ordre 11 qui est le préfixe de 4.
- 11, qui est un des fils de 6, est d’ordre 4 qui est le préfixe de 6.
- 7, qui est le fils de 11, est d’ordre 7 qui est le préfixe de 11.
- 3, qui est un des fils de 8, est d’ordre 9 qui est le préfixe de 8.
En dehors de ces sommets qui sont les points d’articulation, seule la racine 0 a une propriété similaire : son fils 1 est d’ordre 1 qui est le préfixe de 0.
Calcul de ord
On suppose dans la suite qu’on dispose d’une fonction de ce genre qui soit en O(|V|+|E|) :
def D(s):
desc = set([s.sommet])
for t in s.children:
desc = desc.union(D(t))
return desc
def calcule_ord(listes_adjacences):
def V(S):
vois = set([])
for s in S:
vois = vois.union(set(listes_adjacences[s]))
return vois
def ordre(s):
return min([prefixe[j] for j in V(D(s))])
ord = [0] * len(listes_adjacences)
def DFS(arbre,s,vus=[]):
vus.append(s.sommet)
ord[s.sommet] = ordre(s)
for t in s.children:
if t.sommet not in vus:
vus = DFS(arbre,t,vus)
return vus
a,prefixe = parcours(listes_adjacences)
DFS(a,a)
return ordAvec le graphe de l’énoncé cette fonction renvoie
[1, 1, 1, 9, 9, 1, 1, 7, 7, 11, 4, 4, 9]
Question 42
Une fonction qui correspond à la demande est
def points_articulation(listes_adjacences):
arbre,prefixes = parcours(listes_adjacences)
ord = calcule_ord(listes_adjacences)
pa = []
def parcours_prefixe(arbre,s,vus=[]):
nonlocal pa
i = s.sommet
vus.append(i)
if any(ord[t.sommet]==prefixe[i] for t in s.children):
pa.append(i)
for t in s.children:
if t.sommet not in vus:
vus = parcours_prefixe(arbre,t,vus)
return vus
parcours_prefixe(arbre,arbre)
if len(arbre.children)==1:
pa.remove(0)
return paComme elle est basée sur un parcours en profondeur de l’arbre couvrant, elle est en O(|V|+|E|).
Question 43
Les composantes biconnexes du graphe de l’énoncé sont
- 0,1,2,5,6,10
- 3,4,8
- 7,8,11
- 4,9
- 6,11
- 8,12
Soit 6 composantes biconnexes.
Question 44
Comme chaque point d’articulation sépare deux composantes biconnexes, on est tenté de regarder à quoi ressemble le graphe auquel on a enlevé les points d’articulation :
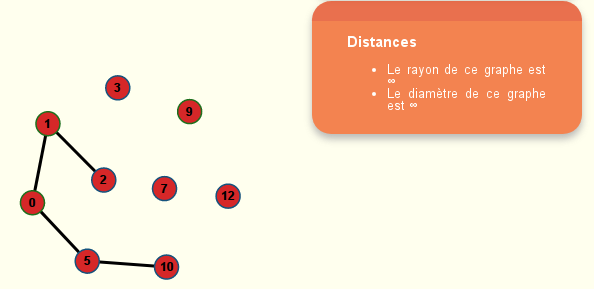
On voit qu’il y a 5 composantes connexes et chacune correspond à une composante biconnexe du graphe de départ. Où est passée la 6e composante biconnexe ?
En fait l’arête 6-11 (une composante biconnexe) joint deux points d’articulation, elle a donc disparu lorsque ses extrémités ont été supprimées.
On suggère donc cet algorithme :
- calculer les points d’articulation
- calculer le graphe privé des points d’articulation
- pour chacune des composantes connexes de ce graphe, remettre le point d’articulation qui y était : cela donne une composante biconnexe du graphe de départ
- chercher les arêtes joignant deux points d’articulation : ce sont elles aussi des composantes biconnexes.
Cet algorithme est de Hopcroft et Tarjan en 1973 :





Commentaires