La maîtrise de l’ensemble des correspondances graphèmes-phonèmes, qui va des lettres ou groupes de lettres vers les sons et réciproquement, est un enjeu essentiel de l’apprentissage du français.

Le travail de lecture est constamment mené en lien avec l’écriture

À l’école maternelle, les élèves ont ... découvert la fonction de l’écrit et commencé à écrire ... principe alphabétique ... régularités de la langue ...

Il s’agit pour les élèves d’associer lettres ou groupes de lettres et sons, d’établir des correspondances entre graphèmes et phonèmes. L’apprentissage systématique de ces correspondances est progressivement automatisé

Compétences :

− identifier des mots de manière de plus en plus aisée ;
− copier ;
− utiliser des stratégies de copie pour dépasser la copie lettre à lettre : prise d’indices...
− savoir discriminer de manière visuelle et connaître le nom des lettres ainsi que le son qu’elles produisent ;

Attendus de fin de cycle

identifier des mots rapidement : décoder aisément des mots inconnus réguliers, reconnaître des mots fréquents et des mots irréguliers mémorisés

Il n’est pas nécessaire d’être lecteur pour commencer à écrire

Les élèves prennent plaisir à écrire sous le regard bienveillant de l’enseignant.

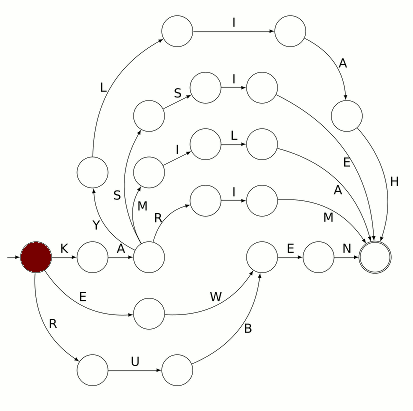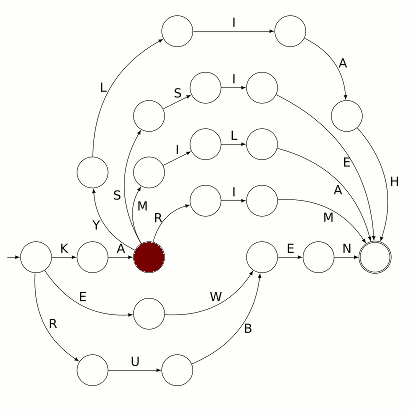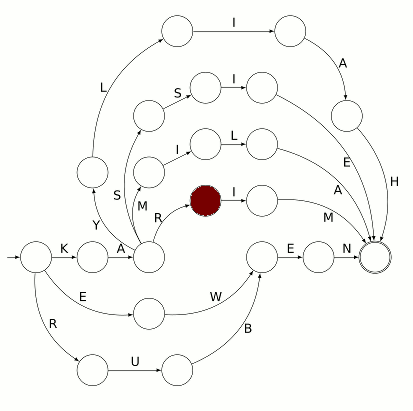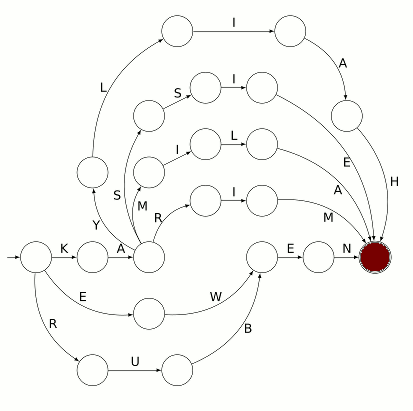
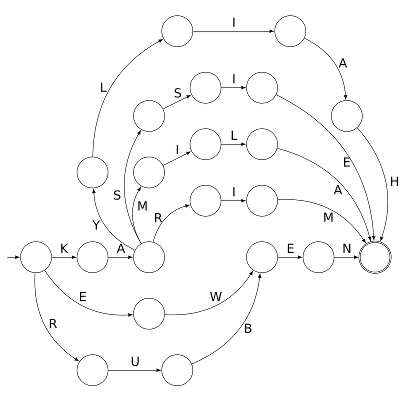
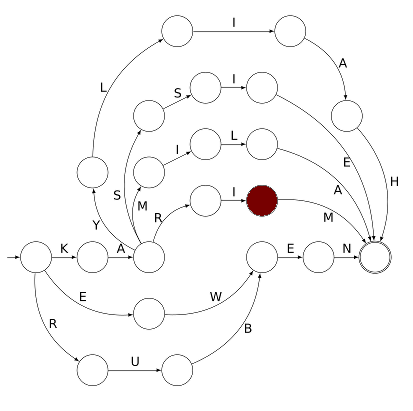
Voici un automate reconnaissant des prénoms d’élèves de CP :

Les élèves dont le prénom figure sur cet automate ont été invités à jouer dessus, à l’aide d’un pion (représentant le Petit Poucet qui sème des lettres au lieu de cailloux). Il leur a été racontée l’histoire du Petit Poucet puis expliqué qu’on allait faire l’inverse (ramasser les étiquettes au lieu de les semer).

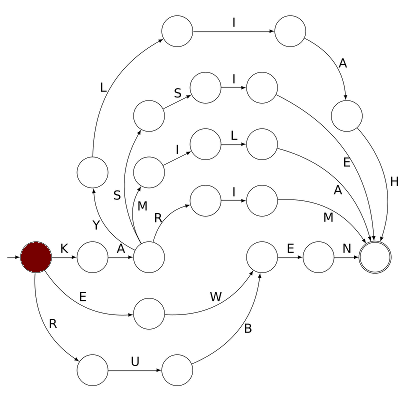
Pour savoir où disposer le pion avant de jouer, il faut repérer, parmi les sommets du graphe, celui qui tient lieu de départ. Ne disposant pas d’un panneau avec écrit « départ » dessus, on s’est contenté de planter un javelot au point de départ. Ce javelot est visible sur la gauche :

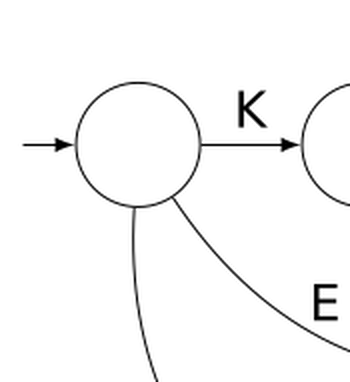
Le pion posé au départ signifie que l’automate est dans son état initial qui signifie « je n’ai encore rien lu » :

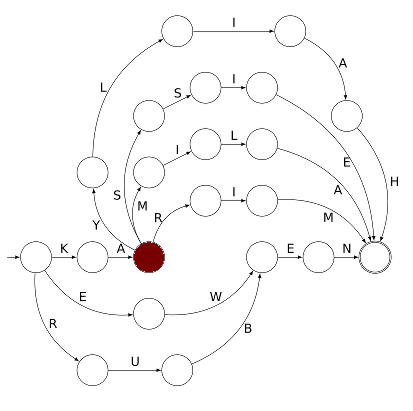
Il est alors possible de choisir un début de trajet entre trois possibilités car le point de départ est un carrefour. En choisissant de suivre la flèche la plus courte, le pion va dans un état signifiant « je reconnais la première lettre du mot, c’est un K » :

Comme on n’a pas le droit de remonter une flèche (ce serait brûler un sens interdit), le pion ne peut alors que continuer tout droit et arriver à un état signifiant « j’ai reconnu la première syllabe du prénom, c’est KA » :

Mais là aussi il y a un choix à faire (entre 4 trajets car le préfixe KA est commun à 4 prénoms de la classe de CP). Si le choix le plus à droite est effectué, on arrive à cet état :

ce qui suppose que l’étiquette R a été ramassée au passage et l’état actuel de l’automate se résume à « je sais que le mot en cours de lecture commence par KAR ». Ensuite le trajet ne comporte plus d’embranchements et il est automatique (c’est le cas de le dire !) d’aller jusqu’au bout du trajet. D’abord

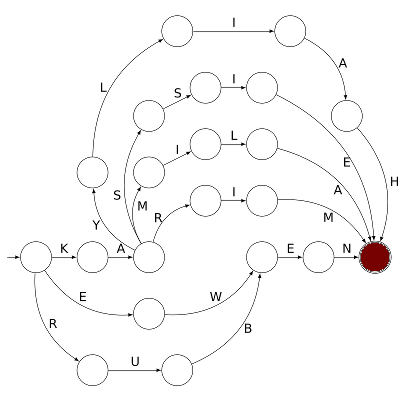
qui correspond à l’état « j’ai lu le mot KARI ». Mais l’état n’est pas final et le mot KARI n’est pas reconnu par l’automate [1], il ne reconnaît que les mots dont la lecture mène l’automate depuis l’état initial vers un état final. C’est ce qui se passe juste après :

En effet l’état dans lequel se trouve actuellement l’automate est final, comme le montre le double trait utilisé pour tracer le cercle. Le trajet suivi par le pion a amené l’automate à reconnaître le prénom KARIM. Il y a 5 autres prénoms que l’automate pouvait reconnaître, et bien entendu ce sont les prénoms des élèves ayant joué sur cet automate.

Le codage ci-dessous est inspiré par les travaux de David Huffman en 1952.

Pour coder un mot, on utilise un dictionnaire (de Python), donnant pour chaque lettre du mot à coder, son code :

codage = {  'S': '✽', \
            'A': '♥✽', \
            'N': '♥♥✽', \
            'I': '♥♥♥✽', \
            'T': '♥♥♥♥✽', \
            'E': '♥♥♥♥♥' }

Pour coder le mot « NINA », on initialise au mot vide la variable code à laquelle on ajoute, par concaténations successives, les codes associés aux lettres du mot « NINA » :

code = ''
for lettre in 'NINA':
    code += codage[lettre]

Après exécution de ce script, la variable code contient le mot ♥♥✽♥♥♥✽♥♥✽♥✽ qui est la version codée de « NINA ». Pour faire l’inverse (décoder et passer par exemple de ♥♥✽♥♥♥✽♥♥✽♥✽ à NINA), il faut le transducteur ci-dessus [4].

Chaque état du transducteur est représenté par un nombre entier (de 0 à 4 pour les 5 états du transducteur ci-dessus). Le transducteur est donc une liste indexée par les états internes. Mais quoi mettre dans cette liste ? À chaque lettre lue il faut associer deux choses : le nouvel état et la lettre (ou le mot, éventuellement vide) écrite. Ces deux choses sont placées dans un couple du type (état,mot) et indexé par la lettre lue. Le tout est placé dans un dictionnaire de Python (par ligne) que voici :

transducteur = [ {'✽': ('S',0), '♥': ('',1)}, \
                {'✽': ('A',0), '♥': ('',2)}, \
                {'✽': ('N',0), '♥': ('',3)}, \
                {'✽': ('I',0), '♥': ('',4)}, \
                {'✽': ('T',0), '♥': ('E',0)} ]

L’avant-dernière ligne (indexée par 3) signifie que dans l’état 3, s’il lit un ✽, l’automate écrira un I en revenant à l’état 0, et s’il lit un ♥, l’automate ira dans l’état 4 sans rien écrire.

Pour utiliser ce transducteur pour décoder le mot ♥✽✽✽♥♥♥✽✽♥♥♥♥✽♥✽♥♥✽♥♥♥♥✽♥♥♥♥♥✽, on initialise à 0 une variable état et au mot vide la variable mot (à écrire en décodant) puis, pour chaque lettre du mot ♥✽✽✽♥♥♥✽✽♥♥♥♥✽♥✽♥♥✽♥♥♥♥✽♥♥♥♥♥✽, on lit dans le dictionnaire transducteur[état], à la lettre lue, un glyphe à écrire et le nouvel état de la machine. En Python ça donne

état = 0
mot = ''
for lettre in '♥✽✽✽♥♥♥✽✽♥♥♥♥✽♥✽♥♥✽♥♥♥♥✽♥♥♥♥♥✽':
    glyphe,état = transducteur[état][lettre]
    mot += glyphe

Après avoir exécuté ce script, la variable mot contient le mot décodé. En cas d’erreur le mot ressemble au « vrai » mot (ordre des lettres inversé ou une lettre remplacée par une autre) ce qui amène à la question suivante :

Le poids de Hamming d’un octet est le nombre de chiffres « 1 » dans l’écriture binaire de cet octet. On peut le calculer par cette fonction Python qui compte les « 1 » après avoir traduit en binaire :

def weight(n):
  return bin(n).count('1')

La représentation graphique de cette fonction (effectuée par la Numworks) montre qu’elle prend des valeurs assez faibles (de 0 à 8 pour un octet) :

Si on considère deux nombres entiers (vus comme mots binaires), le poids de Hamming de leur différence (chiffre par chiffre, notée par un chapeau en Python) est une distance [5] : la fameuse distance de Hamming :

def distance(a,b):
  return weight(a^b)

Programmée sur la Numworks, voici la représentation graphique de la distance de Hamming (noir pour 0, blanc pour le maximum) :

La distance de Hamming ne se définit pas que sur des mots binaires :

La distance de Hamming entre les mots « adonner » et « donnera » (tous deux de longueur 7) est 6, au vu des lettres qui diffèrent entre adonner et donnera. Cela signifie qu’il faut effectuer 6 remplacements de lettres pour passer de l’un à l’autre :

adonner
ddonner
doonner
donnner
donneer
donnerr
donnera

Pourtant il y a plus rapide, en enlevant la première lettre de « adonner » et en la plaçant à la fin, on a directement « donnera ». Cela représente deux opérations seulement :

adonner
donner
donnera

Vu en BTS : un calcul d’intégrale là où on demandait un intervalle de fluctuation (certes il y a un lien, puisque la probabilité qu’une variable aléatoire normale appartienne à un intervalle, est une intégrale). En écrivant sans accent le mot « integrale » on le place à distance de Levenshtein 3, du mot « intervalle », avec ces étapes :

integrale
interrale
intervale
intervalle

Une distance aussi faible peut expliquer la confusion.

Entendu en terminale (par plusieurs élèves) : Un exposant n’est jamais négatif.

Il ressort d’une discussion avec les élèves, qu’il y a eu confusion entre les mots exposant et exponentielle (là encore il y a un lien sémantique entre ces notions, l’exponentielle de x résultant de l’élévation de e à la puissance x qui joue donc le rôle d’exposant [6]).

Mais les mots sont à distance 7, au sens de Levenshtein, comme le montre la plus petite suite de modifications pour aller de l’un à l’autre :

exposant
exponant
exponent
exponenti
exponentie
exponentiel
exponentiell
exponentielle

Il y a donc probablement une confusion partiellement sémantique à l’origine de ce phénomène. Un peu comme le lapsus de Dominique de Villepin qui a prononcé « démission » au lieu de « décision », pas seulement parce que la distance de Levenshtein entre ces deux mots n’est que 2, mais aussi parce qu’à cette époque le sujet de sa propre démission était d’actualité.

Ce document montre un exemple de ce que donne une mauvaise reconnaissance des mots, et il s’agit d’un énoncé de mathématiques :

Monsieur etma damare novon deupari achameau nit. Ladisten cet deux 600 Km lavoix tureconsso me 10 litr rausan quil aumaître. Ilfocon thé 18€ deux pé âge d’aux taurou tet 8€ dere papour désjeu néleumidit. Les sens kou tes 1€ leli treu ilpar ta 8 eureh. Kélai laconso mas siondes sans ?
Quélai ladaipan setota lepour levoiaje ?

On imagine la difficulté de résolution de ce problème, qui se pose à celui qui a tant de mal à saisir la structure de l’énoncé.

Un exemple vu en BTS : Dans le sujet groupement D de 2006 on demandait ceci :

3.Déduire de ce qui précède P(C).

Environ le tiers de la classe a cherché un événement (voire un nombre) qui peut précéder P(C)... C’est plus du triple de la prévalence des troubles dys et il faut chercher l’explication ailleurs que dans le fait de ne pas avoir vu « de » après le verbe « déduire » : Une déduction se fait à partir de quelque chose et cela ne semble pas toujours évident pour des élèves post-bac (qui ont appris à lire à une époque à laquelle on ne pratiquait plus guère la méthode globale).

Vu en 2^nde : L’énoncé de l’exercice était

Calculer le pgcd de 27 et 36

Plusieurs élèves ont rempli toute une page de calculs pour calculer le pgcd de 27 [7] ! Une simple erreur de lecture ne suffit pas à expliquer ceci : même si l’énoncé avait été lu « calculer les pgcd de 27 et de 36 », le sens de l’expression « pgcd » et en particulier le fait que la lettre « c » veut dire « commun » n’est pas connu de ces élèves.

Pour relever le niveau en mathématiques des élèves, il ne suffit donc pas de leur faire travailler la grammaire : le vocabulaire aussi est déficient chez certains élèves. Ce qui semble manquer le plus ce sont les définitions dans le cours. Dans ce document éduscol il est fait le constat que

l’enseignement des mathématiques utilise aussi des mots non encore définis, ou mal définis au moment de leur utilisation ... . Ces mots sont alors manipulés avant de correspondre à une définition mathématique, parfois pendant plusieurs années (la notion d’angle en est un très bon exemple).

Une remédiation possible est de mettre des définitions dans un outil de type guide de survie. Une autre, évoquée dans le document éduscol ci-dessus, est la confection collective d’un dictionnaire.

Voici une liste de définitions données en début d’année scolaire de BTS 1^re année, présentées comme ce qu’il faut connaître pour éviter de trop grandes difficultés conceptuelles :

le document	le source en LaTeX

L’ensemble des nombres réels est muni d’une relation d’ordre dense, ce qui signifie que si a est inférieur à b, il y a toujours un réel entre a et b. Ce fait (à l’origine de l’analyse réelle) est plus aisé à conceptualiser pour qui est familiarisé avec le passé composé et le futur antérieur qui expriment cette idée pour le passage du temps.

Dans le cadre de l’enseignement scientifique, tous les élèves de 1^re générale doivent savoir prouver que le cycle des quintes est infini, c’est-à-dire qu’il n’existe aucune puissance de 3 dont le quotient par une puissance de 2 soit égal à 1. C’est un excellent exemple de démonstration par l’absurde :

S’il existait a et b tels que la fraction 3^a/2^b était égale à 1, on aurait (par produit en croix) l’égalité entre 3^a et 2^b. Or cela est impossible (car 2^b est pair et 3^a est impair) donc l’hypothèse de départ aussi est impossible : il n’existe pas de puissance de 3 qui, divisée par une puissance de 2, donne 1.

Un tel raisonnement se rédige au conditionnel. Comment voulez-vous que des élèves comprennent (a fortiori produisent) ce genre de raisonnement, s’ils ne sont pas à l’aise avec le conditionnel ?