Succès constant
Les jeux sur graphes, les tangrams, les nomogrammes étaient également présents cette année et restent des valeurs sûres pour pérenniser le succès du stand de l’IREM.
De nouvelles formes de pions ont été testées pour les jeux de Fraenkel (Arrows et le jeu de Jupiter).
Nim
Une nouveauté cette année, des pions en forme de coccinelle pour animer un peu les jeux de Nim :

Le succès des jeux « beat Doug » et « beat Craig » est croissant.
Lewthwaite
Le jeu de Lewthwaite, connu depuis quelques années par les habitués de la fête de la science, conserve son succès. Il n’est pas rare de voir des joueurs passer plus de temps à positionner les jetons au début du jeu, qu’à jouer, tant les parties sont parfois très courtes.
Ici ce sont les rouges qui ont gagné :

pourtant les bleus, qui jouent en premier, semblent avoir l’avantage sur les rouges. D’ailleurs ici les bleus ont gagné :

Arrows
Aux échecs, les pions sont plus hauts que larges afin de faciliter leur préhension. Une tentative a été faite cette année pour le jeu arrows qui lui aussi bénéficie d’un grand succès à partir du cycle 3 :
Voici le début du jeu avec ces nouveaux pions :


Ici les bleus ont l’avantage :

Ici aussi :

Une manière possible pour prendre un pion consiste à le renverser pour le faire tomber et rouler puis prendre la place qu’il vient de libérer et enlever du plateau de jeu le pion tombé :

Une autre manière consiste à pousser le pion avec l’attaquant pour prendre sa place et l’enlever ensuite :

On peut aussi poser le pion attaquant sur le pion attaqué (plus facile avec les jetons plats) :
Cependant, les pions utilisés sont un peu larges et tendent à cacher les pointes des flèches ce qui perturbe les joueurs.
Même avec des jetons plus petits (et plus plats) il est parfois difficile de percevoir les menaces. La situation ci-dessous n’est pas sans évoquer la fourchette (échecs) :

D’ailleurs le jeu arrows possède d’autres points communs avec les échecs (fins de partie, importance de contrôler le centre, avantages tactiques, manière de prendre, etc).
Des collégiens ont inventé une variante où chaque joueur a le droit d’avancer un pion le long d’une flèche (comme dans le jeu classique) ou deux flèches qui se suivent (au choix) :

Jupiter
Le jeu Jupiter et la comète avec ses 17 jetons, a toujours effrayé les visiteurs et personne n’y a pour l’instant joué [1] :
Le nombre de sommets du graphe est très élevé donc les diamètres de ces sommets sont inférieurs à ceux des jetons. On a donc tenté le jeu avec des pions de dames chinoises. Le résultat est beau :



Ceci dit, les pions tombent facilement et il est difficile de maintenir le plateau de jeu dans un état jouable. Une version plus jouable serait une course d’orientation où 17 joueurs humains se déplaceraient en suivant les règles de ce jeu.
binaire
La présentation de la numération binaire a été faite, mais pas par des animateurs IREM : Des élèves du lycée Roland-Garros ont joué au commerce avec des billets de Leibniz :

Comme 128+64+16+8+2=218 on en déduit que l’écriture binaire de 218 est 11011010.
Ils ont également présenté le tour de magie d’Édouard Lucas.
Parmi les nouveautés, on a vu de nouveaux nomogrammes, une nouvelle utilisation du Rover et des jeux de cartes essentiellement consacrés à l’histoire de l’informatique.
IMC
Deux nomogrammes étaient exposés, permettant, pour toute personne connaissant sa taille et sa masse corporelle, de calculer leur IMC ou la superficie de leur peau :

Dans les deux cas, on pose une règle entre les graduations représentant la taille et la masse corporelle pour lire sur la graduation du milieu
| la superficie de la peau | l’indice de masse corporelle |
Rover
-Pour l’année des Mathématiques, le Rover se met en scène-

Il a été proposé cette année de pouvoir déplacer un mobile programmable à partir d’une grandeur physique : la luminosité.Dans l’esprit des nouveaux programmes de Maths-Sciences de la voie professionnelle, cette activité propose l’utilisation d’éléments mathématiques (calcul de moyenne, rotation de 45°, inégalité,...) visualisés par des contraintes sur le pilotage d’un mobile programmable.
Algorithme simplifié
Succinctement :
– On mesure la luminosité dans les 4 directions.
– On calcule la moyenne de ces 4 valeurs.
– Si la luminosité est inférieure à un seuil (paramétré en fonction de la moyenne) on pivote sur soi-même.
– Sinon on avance tout droit.
Après quelques essais, le pilotage devient aisé :
Cartes
L’après-midi à l’IUT de Terre-Sainte a été l’occasion de présenter une première fois le jeu des 7 familles de l’Inria. C’était un moment de faible affluence et peu de visiteurs ont pu y jouer. On a néanmoins pu voir que ce jeu
- permet de connaître des noms de personnages liés à l’histoire de l’informatique ;
- permet d’associer chaque nom à sa famille (à part Turing qui est associé à toutes les familles) ;
- donne des repères chronologiques à l’intérieur de chaque famille.
On a pu également présenter en avant-première le jeu de cartes sur l’histoire des maths et de l’informatique en cours de construction au sein d’un atelier IREM.
Il y a trois manières de jouer :
- Avec uniquement les cartes sur l’histoire des maths ;
- avec uniquement les cartes sur l’histoire de l’informatique ;
- en mélangeant les deux jeux de cartes et en jouant sur une chronologie commune aux maths et à l’informatique.
Voici la règle du jeu avec les cartes sur l’histoire des maths :
- Le maître du jeu mélange les cartes puis les distribue aux joueurs de telle manière que chaque joueur ait autant de cartes que les autres. Les cartes sont données face événement (sans date) au-dessus.
- S’il reste une carte non distribuée, le maître du jeu la place sur la table ; sinon l’un des joueurs (celui qui joue en premier) pose la carte qui est au-dessus de son tas, sur la table.
- Le joueur dont c’est le tour prend alors la carte qui est au-dessus de son tas et la place soit avant soit après la carte qui est déjà posée, selon qu’il pense que l’événement décrit est antérieur ou postérieur à l’événement de la carte posée au début. Par exemple, si la carte initialement posée représente l’irrationnalité de π et la carte à placer représente l’invention des nombres décimaux, le joueur la place avant la carte initiale s’il pense que les nombres décimaux sont connus depuis plus longtemps que l’irrationnalité de π, après la carte initiale sinon.
- Le maître du jeu retourne un instant les deux cartes pour valider ou invalider le placement proposé par le joueur, puis rend la carte au jeu s’il s’est trompé : il doit alors remettre sa carte sur le dessus de son jeu et attendre que ce soit de nouveau à son tour pour refaire un essai.
- Chacun son tour, les joueurs jouent la carte au-dessus de leur jeu :
- Ils insèrent la carte parmi les cartes qui sont déjà sur la table (dans l’ordre chronologique, à l’endroit où ils estiment que s’est déroulé l’événement décrit).
- Le maître du jeu retourne la carte jouée ainsi que celles qui la précèdent et la suivent, pour vérifier que l’ordre chronologique est respecté entre ces 3 (ou 2) cartes.
- Si l’ordre est bon, on passe au joueur suivant,
- sinon le joueur reprend sa carte (la remet au-dessus de son jeu) puis on passe au joueur suivant.
- Le premier joueur n’ayant plus aucune carte a gagné le jeu.

Ici par exemple un joueur estime que la construction des nombres réels a eu lieu au 17e siècle puisqu’il la suppose postérieure au problème du Grand-Duc de Toscane et antérieure aux travaux de Blaise Pascal initiés par le chevalier de Méré :

Ce jeu est intéressant parce qu’il amène les joueurs à verbaliser leur raisonnement comme par exemple ceci :« π est connu depuis plus longtemps que √(2) donc on sait probablement depuis très longtemps que ce n’est pas une fraction ».
Le jeu sur l’histoire de l’informatique semble plus facile car il comporte moins de pièges. Par exemple le noyau Linux s’inspirant d’Unix, est très souvent perçu comme postérieur à Unix. Et un nombre surprenamment élevé de joueurs semble savoir (ou deviner) que la numération binaire date de bien avant les débuts de l’informatique.
Les deux jeux plaisent tellement qu’une fois qu’on a joué à chacun, on veut mélanger les deux jeux pour rejouer sur le nouveau jeu de cartes plus conséquent :
Il y avait 8 cartes sur l’histoire des maths et 8 cartes sur l’histoire de l’informatique. Il y en aura plus lors de la semaine des maths où ce jeu sera présenté à nouveau. Une petite difficulté est posée par Leibniz qui figure dans les deux jeux :
- il est à l’origine du concept de fonction ;
- il fut le premier à écrire des entiers naturels en binaire.
Automates de Kleene
Les jeux présentés ci-dessous ont surtout été joués par des enfants scolarisés à l’école primaire voire trop jeunes pour être scolarisés.
Marie
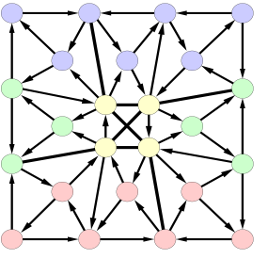
Le pion vient d’arriver à l’arrivée (état final de l’automate, représenté par un double cercle caché par le pion) :
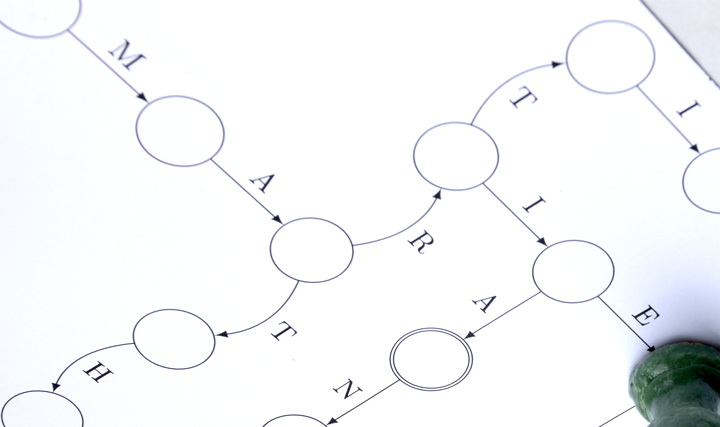
Lors de son premier déplacement, le pion a ramassé l’étiquette « M », puis lors de son second mouvement, l’étiquette « A », et la joueuse a choisi ensuite de lui faire parcourir un chemin comprenant l’étiquette « R » ce qui l’a amené à continuer par les étiquettes « I » puis « E ». En écrivant au fur et à mesure les étiquettes on a construit ce mot :
Bien d’autres mots peuvent ainsi être construits par le parcours d’un pion sur un automate mais seuls ceux qui se terminent sur un état final sont reconnus par l’automate. Le but du jeu était de les trouver tous, et pas seulement MARIE :

Mathilde
Les lettres majuscules sans empattement simplifient la vie du concepteur d’automates de deux façons :
- L’écriture majuscule permet d’éviter les accents et ainsi permet l’utilisation d’une même lettre « E » pour plusieurs mots (en remplacement éventuel de « É », « È » ou « Ê »).
- L’écriture sans empattement simplifie la tâche aux joueurs chargés de recopier les lettres, car ils ont moins de traits à tracer (n’oublions pas que certains d’entre eux sont en cours d’acquisition de l’écriture et ne maîtrisent pas encore les gestes psychomoteurs nécessaires pour écrire).
Cependant, lorsqu’il s’agit de recopier les étiquettes, ceux qui reconnaissent des lettres de l’alphabet français peuvent être tentés de les écrire en attaché :

On voit dans ce cas que la lettre « D » a été transformée en « b » au lieu de « d ». Or si le « b » et le « d » peuvent être confondus parce que ces lettres ont la même forme (du moins en minuscules « scriptes ») ce n’est pas le cas du « B » et du « D » qui n’ont pas le même forme.
Chez cette élève de cycle 3, l’association entre les lettres majuscules scriptes et les lettres minuscules attachées n’a donc pas encore été faite, puisque dans les deux cas il n’y avait pas risque de confusion.
Alors que l’écriture en miroir est décrite comme normale en grande section, on dit qu’en cycle 3 elle pourrait dénoncer un trouble dys. Cependant la production ci-dessus a été faite par une probable élève de Medersa qui pourrait alors être perturbée par les sens d’écriture différents en arabe et en français.
BYOA 1
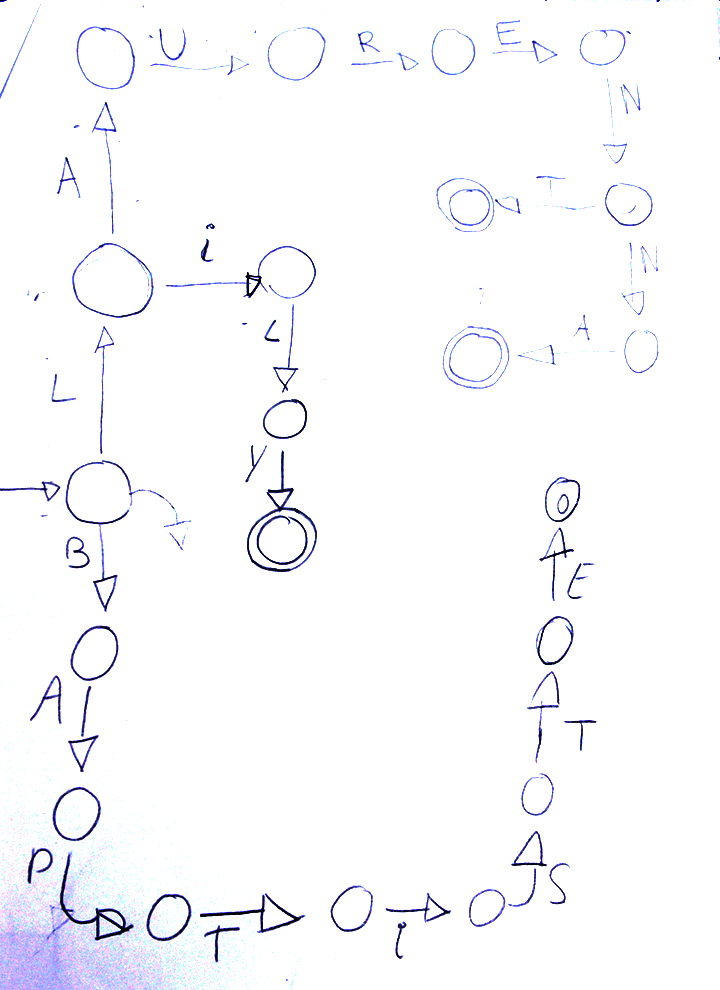
L’abréviation BYOA a été choisie pour désigner l’expression (acronyme) « Build Your Own Automaton » soit, l’activité consistant à construire un automate, avec un crayon, sur une feuille de papier. Ce jeu a été de loin le plus populaire chez les élèves de CM2.
En CP un garçon a rajouté à un automate reconnaissant son prénom, de quoi reconnaître un autre prénom (« NOAH ») :



Deux filles de CM2 ont construit ex nihilo un automate reconnaissant leurs prénoms :


Puis elles ont rajouté d’autres prénoms :
Cet automate a été construit par des CM2 !!!
Une autre élève de CM2 a eu plus de difficultés, car après avoir créé un automate reconnaissant, outre son prénom, celui de « AXIM », elle a corrigé pour qu’à la place ce soit le prénom de « MMAXIM » qui soit reconnu :
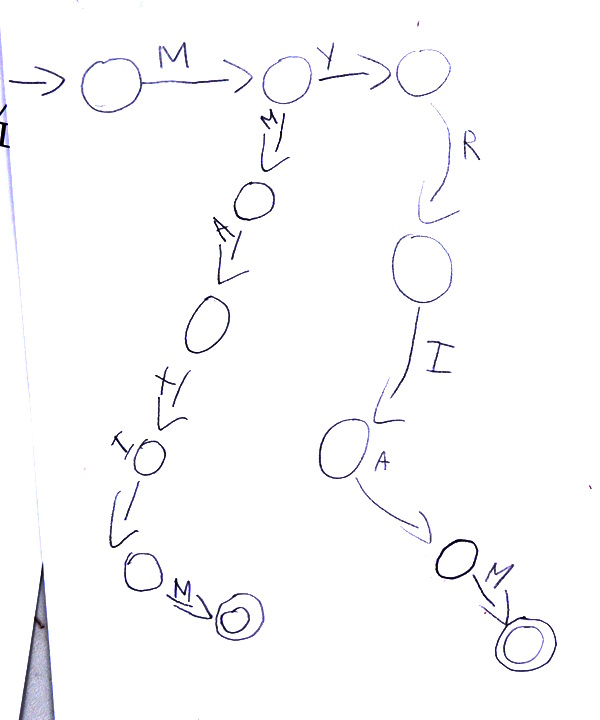
Cela est, à l’évidence, dû à une confusion entre les états (les cercles) et les changements d’état (les flèches).
Remarque du principal intéressé : « Mon prénom se termine par un E. Ce n’est pas MAXIM mais MAXIME ».
wasp
Le mot « GUEPE » aussi est reconnu par l’automate mais moins par les enfants. Ceci dit l’écriture du mot est plutôt aisée (et l’orthographe « GUÊPE » est peut-être plus facile à reconnaître que « GUEPE », nécessaire parce que les autres mots commencent par « GUE » ou « GUÉ »). Voici le début de l’établissement d’une liste de tous les mots reconnus par cet automate :
- Second mot en cours d’écriture :

- Troisième mot écrit :

Jeu : Écrire une historiette marrante où apparaissent les trois mots ci-dessus : « guêpe », « guerrier » et « guéri » (ou « guérie »). Il est possible de rédiger un commentaire à cet effet en bas de cet article.
Voici des errements d’écriture sur la lettre G : Écriture en symétrie centrale mais aussi tentative de recopier les sommets du graphe en plus des étiquettes, au début :
binaire
Les automates suivants utilisent un alphabet dit binaire, à deux lettres. Pour éviter les problèmes de lecture évoqués ci-dessus, on a choisi des symboles plus symétriques (et plus universels) que les lettres et les chiffres de l’alphabet français :
- ✽ représente le chiffre 0 (du moins quand on veut interpréter numériquement).
- ♡ (ou ♥) représentera (quand il s’agira de nombres) le chiffre 1.
Circuits
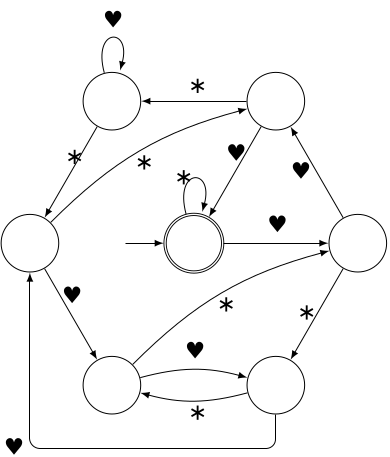
Comme avec les prénoms et les mots en « GUE », les enfants étaient chargés de faire parcourir par le pion (en ramassant des étiquettes) un trajet allant de l’état initial (marqué par une flèche) vers un état final (double cercle). Sauf que là, l’état final est aussi l’état initial. Les étiquettes écrivent un mot binaire correspondant à un circuit (ou cycle) c’est-à-dire un trajet revenant à son point de départ. Voici quelques exemples de circuits choisis par les enfants et leur signification binaire (qui leur a été donnée en récompense à la fin de l’activité) [2] :

♡✽♡✽ ou 1010 en binaire représente le nombre 8+0+2+0=10 en binaire.
♡♡♡♡✽ ou 11110 en binaire représente le nombre 16+8+4+2+0=30 en binaire.

♡✽✽♡✽✽✽♡✽ ou 100100010 représente en binaire le nombre 290.
Voici d’autres mots produits par des visiteurs :

♡♡✽♡✽♡♡♡✽♡ ou 11011101 représente en binaire le nombre 861.
♡♡✽✽✽♡✽♡♡✽ ou 1100010110 représente en binaire le nombre 790.
✽♡✽✽♡✽✽ ou 0100100 représente en binaire le nombre 36.
♡✽✽✽♡ ou 10001 représente en binaire le nombre 17 (qui n’est pas reconnu par l’automate).
♡ représente le nombre 1 (lui non plus n’est pas reconnu par l’automate ; en fait cette élève de CM1 avait passé trop de temps à essayer de colorier ♥ au lieu de simplement dessiner ♡ et avait dû partir, à son grand regret d’aileurs).
✽♡♡♡✽✽♡✽✽✽♡✽ ou 011100100010 représente en binaire le nombre 1826 (non reconnu par l’automate pour la raison évoquée ci-dessus).
♡✽✽♡✽♡ ou 100101 représente en binaire le nombre 37 (non reconnu par l’automate, pour la même raison que plus haut : le trajet n’était pas terminé).
Or le nombre 36 est apparu sur cet automate :
Les nombres 290 et 790 sont apparus sur cet automate :
Le nombre 861 correspond à un circuit sur cet automate :
Quel est le point commun entre ces nombres ? Ou peut-être devrait-on dire « le facteur commun » ? Par exemple quel est le lien entre 290 et 790 ? Pour le savoir on s’est livré à une véritable enquête policière sur ces automates.
5 états
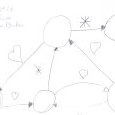
Un vol [3] a été commis au point de départ de cet automate :
Au moment où le vol a été commis, un suspect avait ramassé ces étiquettes : ♡♡♡✽. Dispose-t-il d’un alibi [4] ?
Pour le savoir il faut reconstituer le trajet du suspect sur l’automate. Cela se fait lettre par lettre :
- Au début le suspect a ramassé l’étiquette ♡, il n’a pu le faire que le long de la flèche qui va vers le haut (à droite du dessin ci-dessus). Par conséquent il allait vers le sommet central.
- Ensuite il a ramassé l’étiquette ♡, ce qui s’est fait le long de la seconde flèche (légèrement incurvé) continuant à aller vers le haut. On sait maintenant qu’il était après cela, sur le sommet en haut à droite.
- Ensuite il a à nouveau ramassé une étiquette ♡, ce qu’il n’a pu faire que le long de la flèche allant en diagonale vers le sommet au centre gauche : Ce sommet est son avant-dernière destination avant le vol.
- Enfin il a ramassé une étiquette ✽, ce qu’il n’a pu faire que le long de la flèche verticale à gauche : Au moment du vol il était donc sur le sommet en haut à gauche qui n’est pas le lieu du vol.
Il dispose d’un alibi [5].
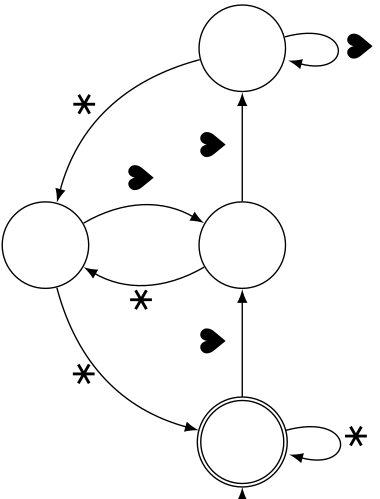
4 états
On a essayé le même jeu avec cet automate :
Ici la position finale du pion étant autre que l’état final (le double cercle à droite) le pion dispose d’un alibi et on barre le mot ♡✽♡✽ qui vient d’être lu par l’automate :

Cela veut dire que le nombre 1010 en binaire (soit, dix) n’est pas reconnu par cet automate. Sur la liste fournie, seuls les nombres 4, 8 et 12 sont reconnus.
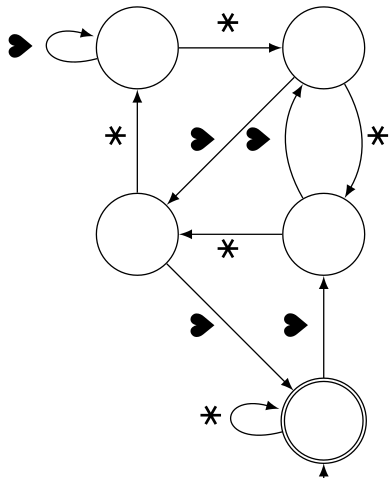
7 états
Les plus hardis se sont attaqués à cet automate avec une longue liste de mots à classer (entre reconnus et non reconnus) :
Avec de l’entraînement cela va de plus en plus vite. Les motifs non barrés sont entourés pour ne pas les traiter deux fois :

On ne voit pas ci-dessous que ♡♡♡ (représentant le nombre 7) est entouré. Mais on voit que 14 (en haut sur la photo), 21 (caché par le médium), 28 (entre le pouce et l’index) et 35 (en bas sur la photo) sont entourés. De fait, une fois la feuille terminée, les autres nombres entourés sont 42, 49, 56 et 63. En CM2 cela parle aux élèves !

Circuit en grand
Le plus gros succès (du moins à Terre-Sainte, car la pluie a empêché de refaire l’expérience au Tampon) a été cette activité mise au point et animée par les élèves de l’Alefpa et leurs enseignants :
Kit
Pour faire une enquête policière dans les normes, il faut à un certain moment faire une reconstitution en grandeur réelle sur les lieux du vol :
Le kit permet de fabriquer un automate à parcourir sur le sol, avec des cercles (les sommets) et des flèches. Pour éviter que les usagers prennent des sens interdits, on a ajouté des panneaux sens interdit :

étiquettes
Ces panneaux sens interdit permettent également de cacher les étiquettes à ceux qui ne doivent pas les voir. Au dos de chaque panneau se trouve une boîte distributrice d’étiquettes qui sont soit des « 1 » en binaire :

soit des « 0 » en binaire :

En voyant sur la feuille quelle est la prochaine étiquette à ramasser, on suit les flèches et on ramasse l’étiquette au passage :

puis on continue jusqu’au prochain sommet :

Ensuite on recommence jusqu’à ce que la liste des étiquettes ait été épuisée. Ceci nécessite donc de lire un mot, lettre après lettre.
Voici les étiquettes qui ont été utilisées lors de la fête de la science :
Les visiteurs montrent souvent du doigt l’étiquette avant d’aller la ramasser, d’autant que certains aiment après avoir joué sur l’automate, conseiller leurs successeurs (là encore en montrant du doigt le chemin à suivre) :
La plus jeune à avoir joué sur cet automate était âgée de moins de 3 ans :
Instructions
Pour se rappeler où on en est dans la lecture du mot binaire, on utilise là aussi l’index comme un pointeur (programmation) :

Par exemple, voici le départ (indiqué par la guide) du trajet, en lisant la première lettre du mot :

puis la lecture de la seconde lettre du mot :

Les visiteurs lisant les étiquettes à ramasser pour guider l’enfant qui bouge (et de ce fait simule un robot) tendent à considérer les lettres du mot comme des instructions.
Mealy
Pour transformer un automate de Kleene en machine de Mealy, il n’y a pas grand-chose à faire avec ce matériel et les enfants interprétant les lettes comme des instructions : il suffit de mettre autre chose que des ♡ et des ✽ dans la boîte (sur les étiquettes) et de laisser les symboles ♡ et ✽ sur la boîte (repères d’orientation sur le trajet). Voici un automate de Mealy permettant de décoder un code de Huffman :
Il sera présenté lors de la semaine des maths 2020, avec ces mots à décoder :




































































Commentaires