Et que peut-on faire avec un registre ? Semer des graines dedans, ou en prélever. Du moment que c’est l’une après l’autre.
On va appeler A, B, C etc les différents registres qui seront idéalement représentés par des boîtes avec les lettres A, B, C etc écrites dessus. Chaque registre contient un nombre entier, représenté par des graines placées dans la boîte. Par exemple si A=8, c’est qu’on a 8 graines dans la boîte A :
algorithmes
Les algorithmes suivants sont à tester en séquence. Dans chaque cas, il est vivement recommandé de faire les manipulations avec des graines de haricot dans des boîtes.
Les trois blocs suivants sont disponibles :

R est un registre quelconque, on peut remplacer la lettre R par toute autre lettre. Autrement dit
- on peut toujours ajouter une graine dans un registre (« incrémenter le registre »), quel qu’il soit ;
- on peut toujours enlever une graine d’un registre (« décrémenter le registre ») non vide, quel qu’il soit ;
- on peut toujours exécuter des instructions en boucle jusqu’à ce qu’un registre donné soit vide.
Vidange
Que fait cet algorithme ?
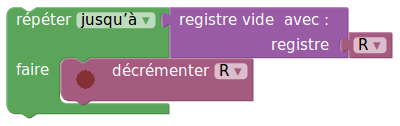
Tester avec 4 graines initialement placées dans R.
Une fois compris le principe de l’algorithme, on peut considérer qu’on a une nouvelle instruction, en se contenant de donner un mot (le verbe « vider ») à l’algorithme :

Et on peut admettre dans la suite que l’on ne vide plus un registre graine par graine, mais en versant directement la totalité de son contenu dans le réservoir de graines.
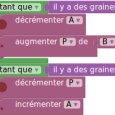
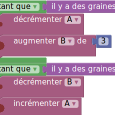
Incréments
Tester sur un registre contenant initialement 2 graines, le premier des deux blocs d’instruction ci-dessous :

On se proposera par la suite de résumer les trois incrémentations par le bloc ci-dessus« augmenter R de 3 ».
Initialisation
Qu’est-ce qui se passe si on ajoute 3 graines à un registre, après avoir vidé celui-ci ?

On dit qu’on a fait une affectation du registre R, par la constante 3. Pour affecter par une variable, il faut savoir comment on peut copier le contenu d’un registre dans un autre.
Transfert
Que fait cet algorithme ?

Tester
- avec 3 graines dans A et B vide au début. Quel est l’effet final ?
- avec 3 graines dans A et 5 graines dans B au début. Quel est l’effet final ?
Copie
Quel est l’effet de cet algorithme ?
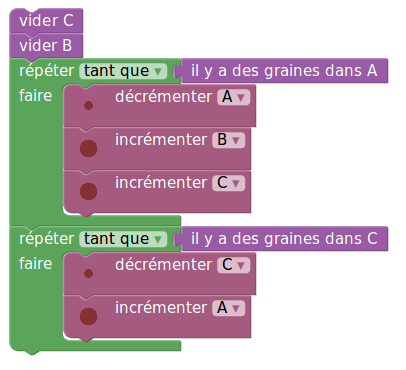
Remarque : Il est possible de faire la fin d’un seul coup, en vidant toute la boîte C directement dans la boîte A :

On convient d’appeler transférer C dans B l’opération consistant à verser le registre C dans le registre B. Si B n’était pas initialement vide, que se passerait-il après transfert de C dans B ?
Addition
Que fait l’algorithme suivant ?
Tester avec les conditions initiales suivantes :
- 3 graines initialement dans A et 5 graines initialement dans B
- 5 graines initialement dans A et 3 graines initialement dans B
- 3 graines initialement dans A et B initialement vide
- A initialement vide et 3 graines initialement dans B
- A et B initialement vides
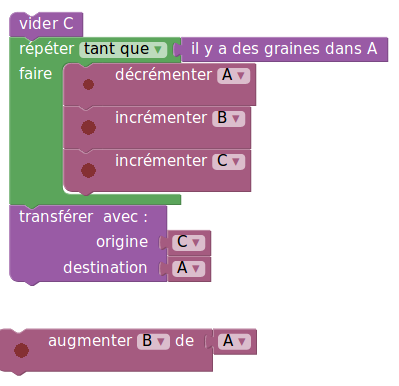
On convient d’appeler augmenter B de A le résultat de cet algorithme.
Que fait alors l’algorithme suivant ?
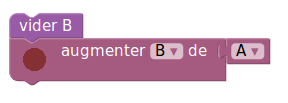
Exemples
Le modèle des machines de Minsky est Turing-complet. Cela veut dire, essentiellement, que les opérations sont toutes calculables avec ce modèle. On a déjà vu l’addition et la multiplication par une constante, reste à voir les autres opérations.
Soustraction
Comme on ne modifie pas une différence en décrémentant les deux opérandes, le script suivant devrait pouvoir facilement effectuer une soustraction, par exemple en mettant 13 graines dans A et 8 graines dans B, à la fin il reste 13-8=5 graines dans A et B est vide :
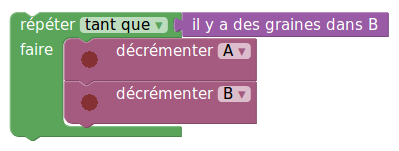
Mais pour que cet algorithme effectue vraiment une soustraction A-B, il faut qu’il y ait plus de graines dans A que dans B : On n’effectue que la soustraction des entiers naturels et elle n’est définie que pour A plus grand que B.
L’algorithme suivant est une amélioration :
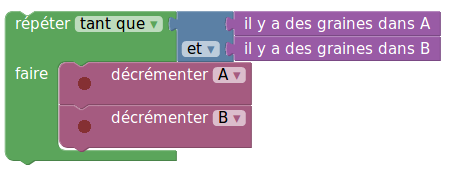
Mais il calcule la valeur absolue de la différence :
- Si A est plus grand que B, A-B se retrouve dans A à la fin, et B est vide.
- Si B est plus grand que A, B-A se retrouve dans B à la fin, et A est vide.
Dans l’onglet sur l’algorithme d’Euclide, on étudie un prolongement de cet algorithme.
Enfin voici un algorithme correspondant plutôt bien à ce qu’on attend d’une soustraction :
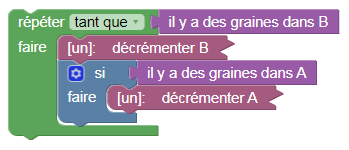
En effet si A contient initialement plus de graines que B, la boucle s’arrête lorsque B est vide, et à ce moment-là, A contient la différence. Si, au contraire, B contient plus de graines que A au début, lorsque A est vide, B continue à se vider et A contient 0, ne pouvant terminer sur un nombre négatif qui serait hors sujet dans le modèle de Minsky.
Comparaison
Cet algorithme est intéressant aussi pour autre chose que la soustraction :

En effet, il met A-B dans A si A>B initialement et B-A dans B si B>A au début, mais aussi il vide le plus petit des registres A et B :
- Si au début A contient plus de graines que B alors B est vide à la fin ;
- si au début B contient plus de graines que A alors A est vide à la fin.
Un simple test de vacuité permet donc de savoir lequel des deux nombres était le plus grand au début : C’est celui qui était dans le registre non vide à la fin.
Si les deux registres étaient égaux au début, ils sont vides tous les deux à la fin.
Division par 2
Cet algorithme divise par deux le contenu d’un registre :

Quand l’algorithme a terminé, B contient la moitié de la valeur initiale de A et A contient 0 ou 1 graine selon la parité de cette valeur initiale :
- B est le quotient euclidien de la valeur initiale par 2
- A est le reste euclidien de la division de la valeur initiale par 2.
Cette opération est utile pour la formule de Pick et pour la suite de Collatz
Cet algorithme effectue la division euclidienne par 3 :
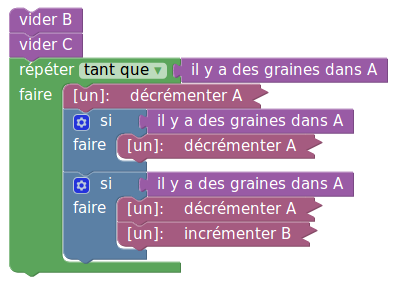
Là encore le reste est ce qui reste dans A, et le quotient est ce qui a été compté dans B.
De même on peut effectuer la division euclidienne par 4 :
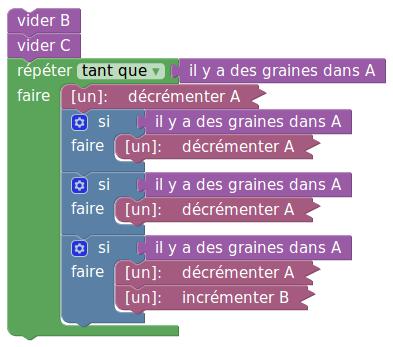
ou par tout autre entier non nul (mais constant : pour la division par une variable voir plus loin)
Multiplication
Une multiplication est une addition itérée :
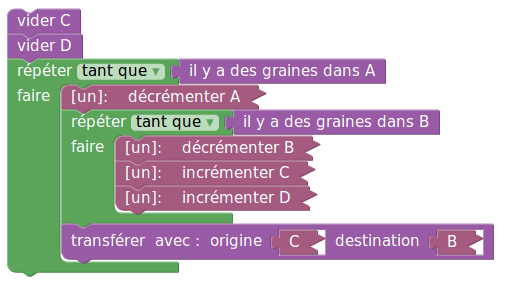
Les mouvements de graines dans la boucle reviennent à
- vider B
- en même temps, copier son contenu initial dans C (« C » comme « copie »)
- mais aussi ajouter le contenu initial dans D qui contiendra donc finalement A copies du registre B (enfin de sa valeur initiale).
Ensuite, il est donc nécessaire de retransférer C dans B afin de pouvoir effectuer la boucle.
Simuler cet algorithme en manipulant les graines de haricot est une excellente initiation à la programmation, parce qu’on touche un peu à toutes les notions fréquentes en programmation :
- A est un compteur (par décrémentation) qui permet de répéter les opérations dans la boucle ;
- D est un accumulateur qui contiendra in fine le produit des valeurs initiales de A et de B ;
- C sert à contenir une copie de B et simule donc une mémoire ;
- A et B sont modifiées ; si on veut les rendre non mutables (comme on le fait en programmation fonctionnelle) il faut les copier avant tout dans d’autres registres temporaires et retransférer ceux-ci dans A et B à la fin.
Voici l’algorithme de multiplication, un peu plus détaillé :
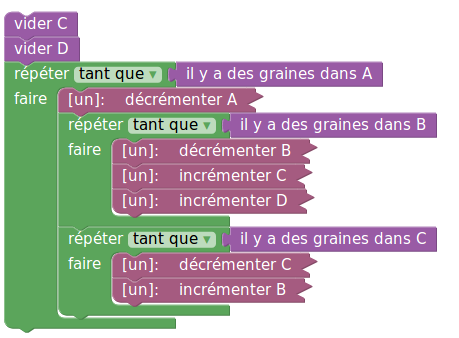
Division
La division euclidienne de A par B peut s’effectuer par des soustractions successives :

On suppose qu’initialement A contient plus de graines que B et on veut calculer le quotient (qui vaut donc au moins 1) et le reste dans la division euclidienne de A par B.
D est un compteur qui va compter (c’est son rôle) le nombre de fois qu’on peut soustraire B à A. Ce nombre est le quotient.
Dans la boucle, on soustrait B à A mais en vidant B. Pour récupérer son contenu initial, on en fait donc une copie dans C. Ensuite on retransfère C dans B. Dans le détail cela se fait ainsi :

Que se passe-t-il si B est vide au début ? Qu’en conclure ?
pgcd
L’algorithme d’Euclide permet par soustractions successives d’obtenir le pgcd de deux nombres initialement stockés dans A et dans B :

Le pgcd se trouve finalement dans C, lorsque A et B sont vides tous les deux.
puissances
Comme la multiplication est une addition itérée, Minsky propose d’aller au stade suivant, avec des multiplications itérées, c’est-à-dire une exponentiation. Cela, conjugué à la divisibilité, permet de faire du codage et du décodage de Gödel, et ainsi, de démontrer que le modèle de Minsky est Turing-complet. Ce n’est pas ainsi que Marvin Minsky a prouvé la Turing-complétude : Il a simulé une machine de Turing universelle avec des registres.




Commentaires