Question 1
Dans MathsOntologie, un point est formé de deux nombres (ses coordonnées) séparés par un arrobase :
| A B C |
A := -1@3.
B := 3@6.
C := 3@1.Les vecteurs également sont représentés par leurs coordonnées, ce qui permet d’additionner des points par exemple ; ceci sera d’ailleurs utile plus bas...
Question 3
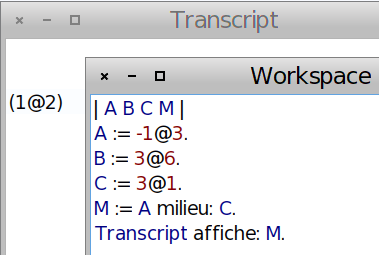
La distance AM n’étant pas décimale, il vaut mieux travailler avec son carré pour garder une précision suffisante :
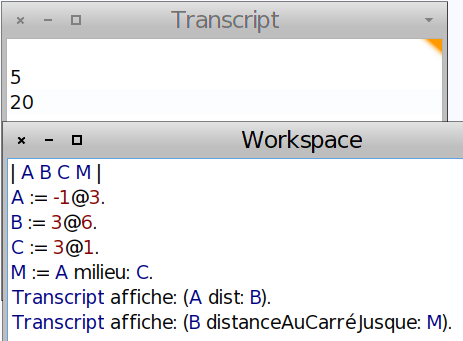
Question 4
On peut commencer par vérifier l’affirmation de l’énoncé :
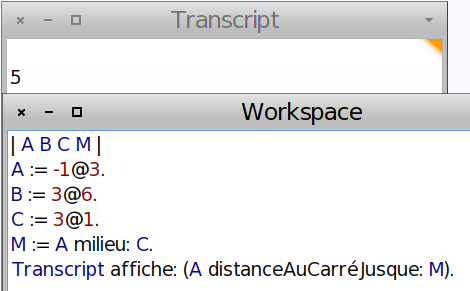
La réciproque du théorème de Pythagore permet alors de vérifier que le triangle est rectangle en M :
On pouvait également utiliser les vecteurs
en vérifiant la nullité de leur produit scalaire :
Question 5
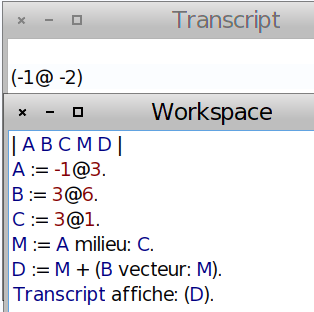
Il y a au moins 3 façons d’obtenir D :
Première manière :
Appliquer à M la translation dont le vecteur va de B à M :
Deuxième manière :
Additionner (selon la notation dite de Grassmann) M avec le vecteur (que Grassmann notait soustractivement M-B) :
Troisième manière :
Constater que par définition, M est le milieu [1] de [BD], et traduire ça en disant que D est le symétrique de B par rapport à M :
Bref, on dirait que D(-1 ;-2)...
Pour la fin de la question, on a un quadrilatère dont les diagonales ont même milieu et sont perpendiculaires ce qui suffit à conclure ; on peut aussi vérifier l’égalité des longueurs de ses côtés :
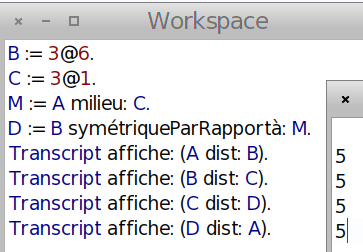
Question 6
L’aire du quadrilatère est le double de celle du triangle, qui elle vaut 5 :
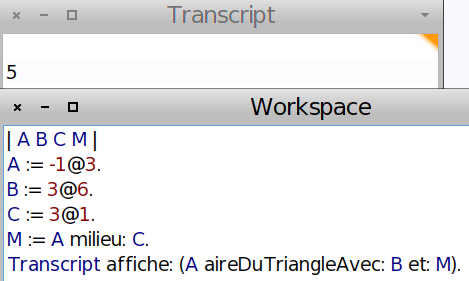
Question 7
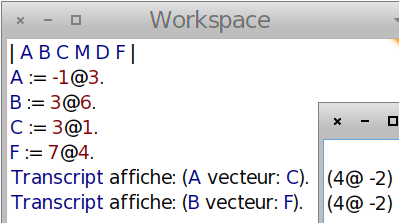
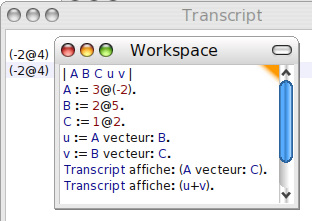
Si les deux vecteurs ont mêmes coordonnées, ils sont égaux et donc ABFC est un parallélogramme ; on voit bien que ce n’est pas un rectangle mais est-ce un losange ?
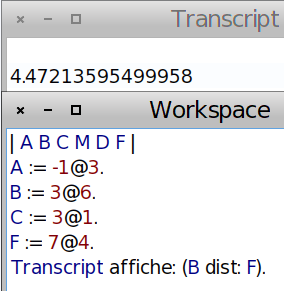
Ah tiens non, BF n’étant pas égale à AB...
Question 8
On a déjà vu à la question 5 comment obtenir E :
opérations sur les vecteurs
Pour additionner deux vecteurs u et v, il suffit d’écrire u+v et pour calculer le triple du vecteur u, d’écrire 3*u. Par exemple, la vérification expérimentale de la relation de Chasles peut se faire avec ce genre d’activité :
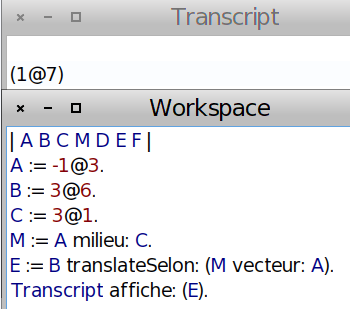
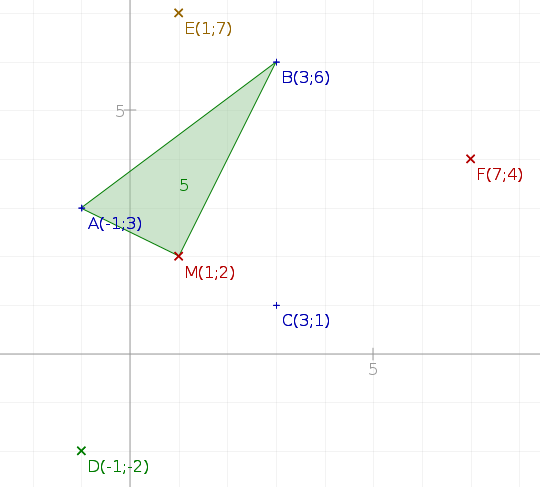
Commentaires