Activités numériques
Exercice 1
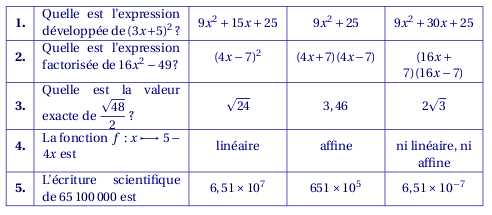
La question 1 se traduit en termes de fonctions : Parmi les trois propositions du QCM, une seule est la même fonction que l’énoncé. Il suffit donc de représenter graphiquement les 4 fonctions sur un même intervalle et de regarder laquelle des trois est identique à celle de l’énoncé ; tout d’abord, la première proposition ne convient pas, comme on s’en rend compte en superposant les deux représentations graphiques (elles sont translucides) :
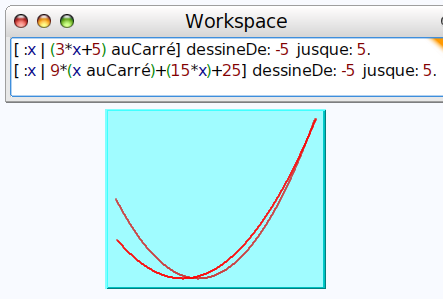
Par contre, la troisième coïncide :
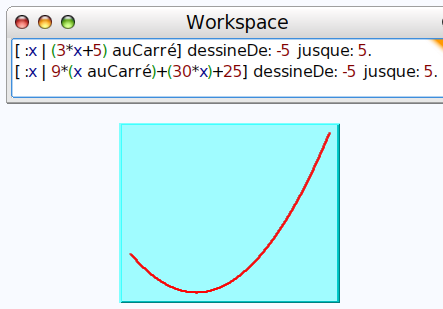
La question 2, se résolvant de manière analogue, ne sera pas traitée ici.
Pour la question 3, on peut faire pareil : Comparer les valeurs numériques à 16 décimales :
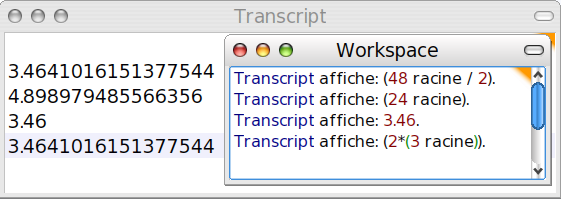
La question 4 étant une question de cours ne sera pas traitée ici...
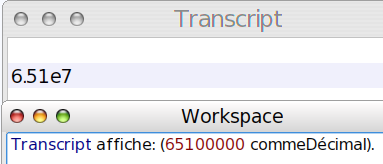
Pour la question 5 on calcule et hop :
Exercice 2

Pour la première question il suffit de faire
Transcript affiche: (6+5)
Mais bon...
Par contre, une fois qu’on a trouvé combien de boules rouges il faut placer, on peut le vérifier par une simulation, consistant à répéter 10000 fois l’expérience consistant à choisir une boule au hasard dans l’urne et répertorier les résultats dans une collection appelée stats :

On voit alors que la fréquence des boules rouges est voisine de 50%.
Question 2
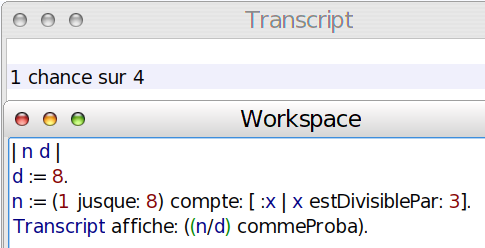
Il suffit de compter, parmi les nombres allant de 1 à 8, combien sont divisibles par 3 ... ou de les faire compter par MathsOntologie :
Par peur que cet article soit copié-collé par des élèves qui veulent tricher pour un DM [1], il ne sera pas répondu ici à la question 3 ; à la place, on peut simuler l’expérience avec MathsOntologie

Le diagramme en bâtons permet d’estimer la probabilité de gain avec la loi des grands nombres.
Exercice 3

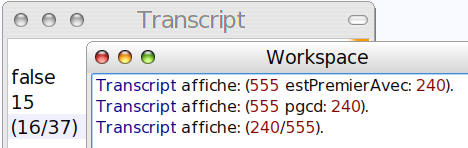
Pour la question 1, « false » veut dire qu’ils ne sont pas premiers entre eux, mais on peut savoir pourquoi, en calculant leur pgcd : On trouve 15, qui n’est pas égal à 1 cqfd :
Activités géométriques
Exercice 1

MathsOntologie ne possédant pas d’objet trapèze, on va couper celui-ci en deux morceaux, l’un triangulaire, l’autre rectangulaire (comme c’est d’ailleurs suggéré sur la figure de l’énoncé).
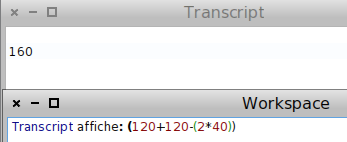
Alors l’aire totale du trapèze est 800+600=1400 m2 et son périmètre est (parce qu’on a compté deux fois en trop le pointillé) 120+120-2 × 40=160 :
Question 1
À 35 m2 correspondent 1 kg, donc à 1400 m2 corrrespondent 40 kg :

La question est donc de savoir à combien de sacs de 15 kg correspondent ces 40 kg ; la réponse n’étant pas entière, et comme tout sac entamé est à acheter en entier, on trouve 3 sacs :
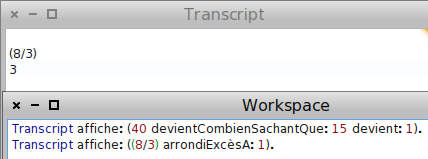
Question 2
Comme 150 m de grillage ne suffisent pas à cloturer 160 m de terrain, la réponse est non.
Exercice 2

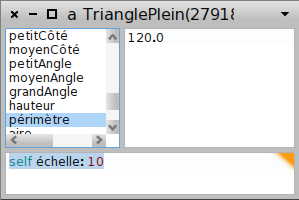
L’objet Triangle est plus difficile à utiliser que les autres objets géométriques, parce que, comme il est difficile de modifier une variable à la fois (à cause de la nécessité de respecter les inégalités triangulaires) il est possible de modifier plusieurs variables en même temps. Aussi le clic droit sur le triangle (qu’on peut au besoin faire apparaître avec TrianglePlein new openInWorld) ouvre-t-il non le menu des autres objets géométriques, mais l’inspecteur de triangles :
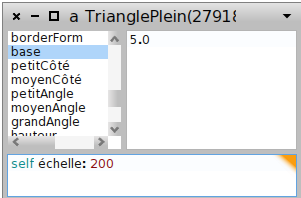
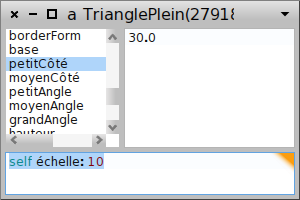
L’inspecteur est muni de son propre workspace (en bas) dans lequel on peut programmer aussi ; pour qu’il devienne possible de modifier la base (le plus grand côté) sans qu’il soit supérieur à la somme des deux autres côtés, on peut modifier l’échelle du triangle ; son ancienne base valant 5 mètres, avec un facteur d’échelle de 200, on passe à 1000 mètres ce qui permet de remplacer par 800 sans problème (ci-dessus) ; l’effet obtenu est celui-ci :
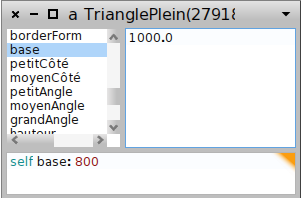
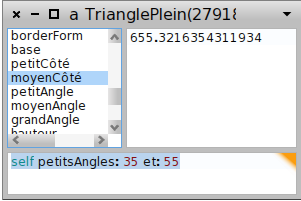
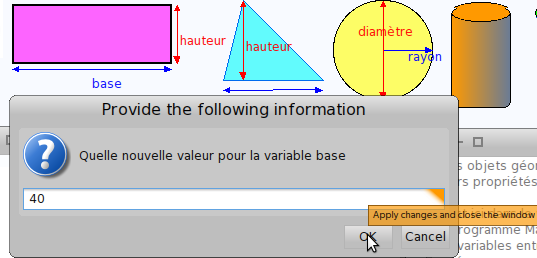
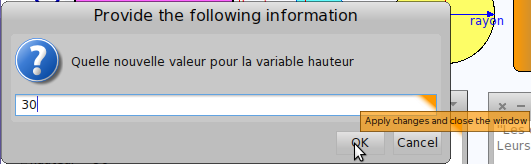
Il suffit alors de remplacer la base par 800 (ci-dessus) pour que la distance entre les deux bateaux soit de 800 mètres. Ensuite on remplace le petit angle par 35 ° et l’angle moyen par 55 %:

Les réponses à la question apparaissent alors dans l’inspecteur, en sélectionnant successivement petitCôté :
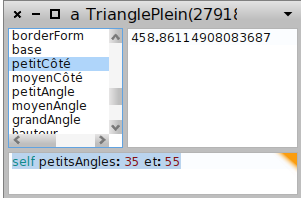
puis moyenCôté :
Exercice 3
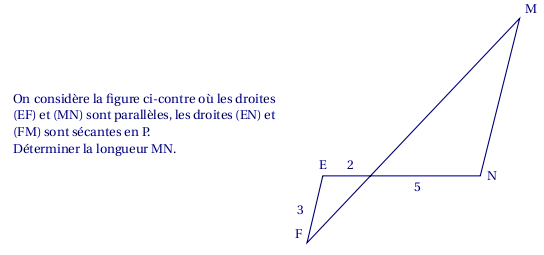
Le théorème de Thalès portant sur des proportionnalités, on peut résoudre cet exercice avec une règle de trois :
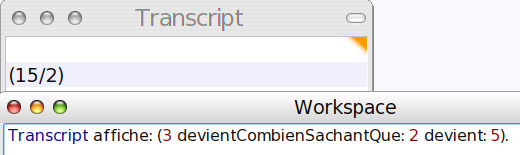
Problème
Le cercle de lancer

On va répondre à la question en deux étapes : Calculer l’aire du disque entier, puis calculer l’aire du secteur circulaire, par proportionnalité.
Aire du disque
Un clic droit sur le disque (si on ne le voit pas, faire Disque new openInWorld dans le transcript) permet de voir ce menu où on choisit le diamètre :
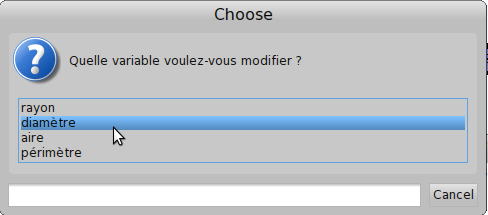
Une fois que c’est fait, on entre le diamètre :
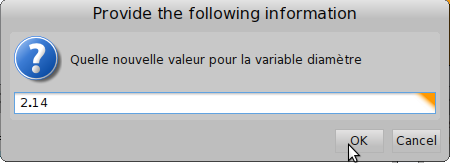
Le clic sur « OK » fait alors apparaître ceci dans le transcript :

On y lit, entre autres, l’aire totale du disque, qu’on peut copier-coller vers le workspace :
Aire du secteur
La question est de savoir ce que devient l’aire totale lorsqu’on passe des 360° du disque aux 40° du secteur :

Une fois la question sélectionnée, il suffit de l’imprimer dans le workplace :
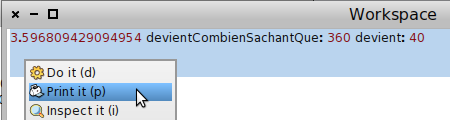
pour avoir l’aire du secteur :
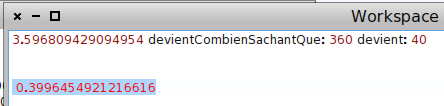
Le poids

La réponse se trouve en deux étapes : Calcul de volume puis calcul de masse à partir de la masse volumique.
Calcul de volume
Un clic droit sur la boule (éventuellement à créer avec Boule new openInWorld) permet de choisir quelle grandeur on veut copier de l’énoncé :
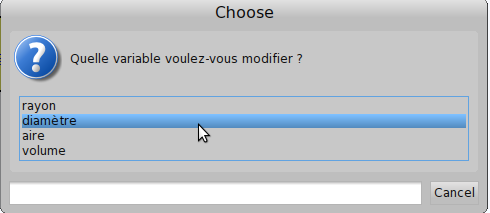
Une fois le diamètre choisi, on n’a plus qu’à entrer sa valeur :
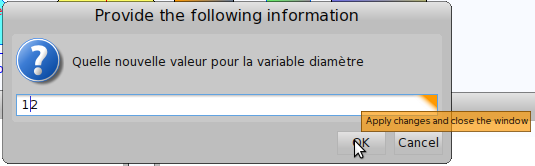
Les réponses (celle qu’on se pose et les autres) apparaissent alors dans le transcript :

Calcul de la masse
Le volume peut être copié-collé depuis le transcript, vers le workspace :
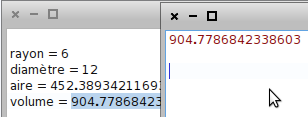
On peut ensuite rajouter la masse volumique :

Au lieu d’écrire le résultat dans le transcript, et pour gagner de la place, on l’imprime directement dans le workspace : On sélectionne le tout, avec « print » :
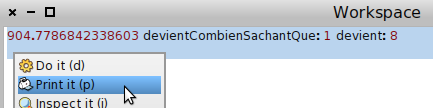
La réponse affichée permet alors de répondre à la question :

Le III, qui ne porte que sur des lectures graphiques, ne sera pas traité ici.
Performances

Question 1
Il suffit de lire les trois derniers éléments de la liste triée :
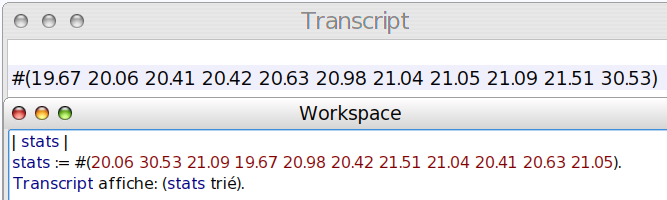
Question 2
On dira 21 mètres 58 à un cm près :
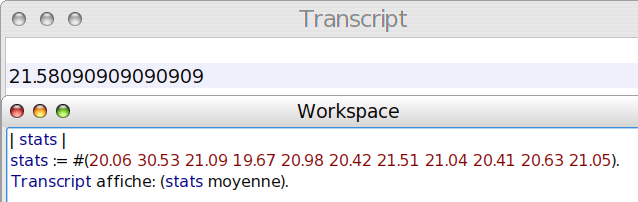
Question 3
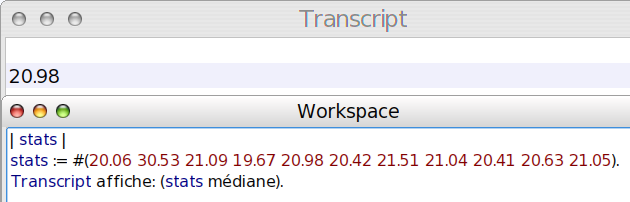
Question 4
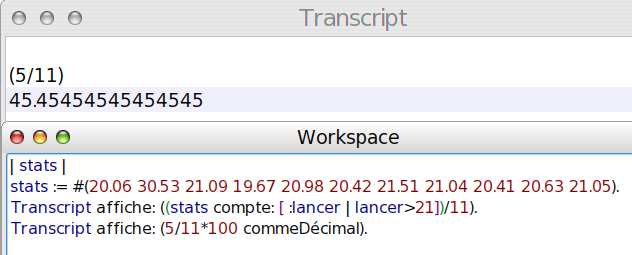
On dira environ 45 pourcents :






Commentaires