1 2 3 4

Le principe des grammaires L (initiale du nom d’Aristid Lindenmayer, botaniste hongrois qui les a inventées) est d’engendrer de longues chaînes de caractères utilisant ces lettres (soit $V=\left\{F,f,+,-,[,] \right\}$) avec des grammaires transformationnelles, puis de soumettre la longue chaîne à une tortue LOGO, qui en l’interprétant, va tracer un polygone, qui sera souvent une approximation d’un objet fractal.

Par exemple, l’ensemble triadique de Cantor peut être codé par la grammaire suivante :

Axiome

$F$

Règles de dérivation

$F \rightarrow FfF$

$f \rightarrow fff$

Dérivation après dérivation à partir de l’axiome, on a la suite de chaînes suivantes :

• $FfF$
• $FfFfffFfF$
• $FfFfffFfFfffffffffFfFfffFfF$
• $FfFfffFfFfffffffffFfFfffFfFfffffffffffffffffffffffffffFfFfffFfFfffffffffFfFfffFfF$

etc.

La chaîne ci-dessus demande à la tortue d’avancer 81 fois, mais en ne laissant une trace par terre que lorsque le "F" est majuscule, ce qui lui fait alors tracer le motif suivant :

- -   - -         - -   - -                           - -   - -         - -   - -

qui est bien une approximation finie de l’ensemble de Cantor.

Sémantique

Dans les figures ci-dessous, on n’utilise qu’une version réduite du langage de la tortue, celle comportant uniquement les instructions

• F : Avancer, mais de combien ?
• + : Tourner à droite, mais de quel angle ?
• - : Tourner à gauche, mais de quel angle ?

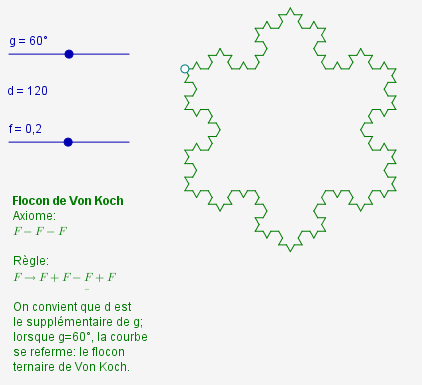
Puisque contrairement à xcas et Python, CaRMetal est un logiciel de géométrie dynamique, autant en profiter pour mettre en mode curseur les variables f (de combien la tortue avance) et d (angle de rotation à droite, l’angle g étant choisi égal ou, selon le cas, supplémentaire à d). Et comme on s’en doute, ces réglages sémantiques changent considérablement l’allure de la courbe fractale, l’exemple voulu n’étant obtenu que pour une valeur bien précise de d.

On va détailler un seul exemple, pour montrer comment on "pense L-systems" : Le flocon de Von Koch :

• L’axiome représente l’allure globale du flocon, qui est un triangle équilatéral ; la recette LOGO pour le triangle équilatéral, c’est

— *avance f
— *tourne droite 120
— *avance f
— *tourne droite 120
— *avance f

mais ici, l’angle d vaut 60° et non 120° ; donc on va plutôt choisir l’autre triangle équilatéral, celui avec la tête en bas, et choisir

— *avance f
— *tourne gauche 120
— *avance f
— *tourne gauche 120
— *avance f

ce qui s’abrège en

F-F-F

• La règle de dérivation (il n’y en a qu’une puisque seul F sera remplacé) est celle qui explique comment aller "dans le détail". Pour Von Koch, au lieu de simplement avancer, on va plutôt faire la suite d’opérations suivantes :

— *avancer
— *tourner à droite (de 60°)
— *avancer
— *tourner à gauche (de 120°)
— *avancer
— *tourner à droite (de 60°)
— *avancer

ce qui se résume par le programme tortue suivant :

F+F-F+F

d’où la règle de dérivation, la récursivité se charge du reste (lancer le script pour voir apparaître la figure ; il est dangereux de changer de figure avant la fin du script ; donc pour essayer d’aller plus loin - changer le nombre de niveaux par "modifier le script" - il est fortement recommandé de télécharger les fichiers au bas de la page et de les utiliser en local)... :

Difficile de parler de langages sans parler de vocabulaire : La troisième figure ci-dessus a été nommée "flocon de neige de Minkowski" par Mandelbrot, qui avait alors attribué à Hermann Minkovski la paternité de cette courbe fractale. Mais dans wikipedia, elle s’appelle "fractale quadratique de Koch", le même nom ayant été donné à celle-ci

qui, ci-dessus, s’appelle "Koch 2". Il a donc été décidé de maintenir le nom de "flocon de Sierpinski" à la courbe fractale de l’onglet 3 ci-dessus...

1 2 3 4