Depuis août 2009, le logiciel s’est doté d’un langage de scripts pour pouvoir travailler la programmation principalement dans un environnement graphique (même si la console texte existe) et surtout un environnement graphique dynamique.
Ce n’est pas sans lien avec l’évolution des programmes du lycée : puisqu’il y a de moins en moins de géométrie mais de l’algorithmique et de la géométrie repérée, pourquoi ne pas envisager de faire se rencontrer ces deux champs là du programme ? Si possible de manière intelligente, voire même ludique …
Du côté de l’élève il s’agit de proposer un environnement commun pour la géométrie et la programmation – économie de temps d’apprentissage – avec un langage non pas construit uniquement pour une utilisation scolaire, avec les artifices qui vont avec (les plus anciens se souviendront que certains d’entre nous ont appris le LSE !!!), mais bien un langage largement utilisé dans le monde Web 2.0 pour lequel les navigateurs rivalisent en temps d’exécution : le javascript (JS).
Introduction aux CarScripts
L’éditeur javascript de CaRMetal intègre toutes les fonctionnalités géométriques du logiciel sous forme d’icônes, ainsi que la bibliothèque Maths du JS et les principales instructions de programmation. L’utilisation du JS est ainsi simplifiée : il n’y a pas de syntaxe à apprendre, on ne fait que modifier des lignes pré-écrites. Les lignes son numérotées (renvoi du numéro de la ligne dans les erreurs) et il y a une coloration syntaxique.
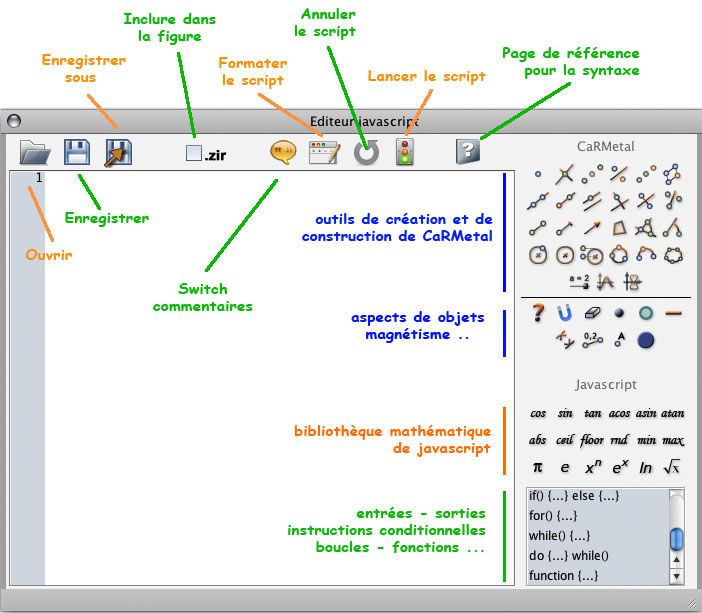
Pour l’auteur, le choix de JS relève d’un cahier des charges très précis : langage pérenne, intégrable dans un logiciel libre, utilisable en ligne, et qui plus est faiblement typé pour pouvoir ajouter les fonctionnalités géométriques de CaRMetal.
Pour les habitués de la programmation en JS, éventuellement pour les premiers usages en classe, l’utilisation peut se faire en « pur JS » avec une sortie en console texte. Cette sortie est simple d’accès et pratique pour tout ce qui peut toucher les statistiques ou l’algorithmique en arithmétique par exemple. On se centrera dans la suite sur la sortie dans une fenêtre de CaRMetal car c’est là qu’est la richesse du langage puisque son intégration à CaRMetal est totalement dynamique comme on va le voir au cours des pages suivantes.
Un script de CaRMetal – on dira désormais un CarScript – peut s’appliquer à une figure vide ou à une figure préparée pour son exécution. Il y a alors deux points de vue différents. Pour le programmeur un CarScript est avant tout un programme qui admet comme paramètre d’entrée une figure de CaRMetal. Pour le géomètre, un CarScript est un outil qui va finaliser une figure que la géométrie dynamique usuelle ne pourrait pas faire – ou pas aussi rapidement. Et selon ce que nous faisons nous sommes parfois plus du côté du programmeur, parfois plus du côté du géomètre.
Le site de l’IREM de La Réunion contient déjà de nombreuses ressources sur les CarSCripts, que ce soit des manuels de référence, polycopiés de formation, et de nombreux scripts, pour la classe ou pour l’enseignant (références en fin d’article). Nous nous contenterons ici, à travers quelques exemples, de mettre l’accent sur l’intérêt de l’utilisation des scripts de CaRMetal pour enseigner à la fois la programmation, la géométrie et l’analyse dans un jeu de cadres riche et qui sait rester dynamique. Nous allons justement commencer par ce qui est peut-être le plus important dans son usage au lycée, quand la géométrie dynamique étend sa compétence à la vérification des scripts par manipulation directe.
GeomDynRep
Géométrie repérée dynamique
Nous allons nous attarder sur ce premier thème, très élémentaire, mais significatif de l’évolution possible de nos pratiques scolaires dans le cadre des nouveaux programmes du lycée. En effet, avec les outils qu’il propose, CaRMetal autorise un nouveau regard sur la géométrie repérée car il permet de faire – très simplement – des programmes autour de ce que nous appellerons de la géométrie repérée dynamique, c’est-à-dire de la géométrie repérée, tournée du côté de l’algèbre, tout en restant accessible à la manipulation directe. Sans aucune technicité, nous utilisons d’emblée cette spécificité dynamique de l’interaction JS-logiciel. Voyons comment sur l’exemple de la construction algébrique d’un carré, en plusieurs étapes.
Tout d’abord, commençons par un carré particulier, centré à l’origine O du repère, et de sommet A. Pour l’essentiel, il suffit donc de savoir placer un segment orthogonal à [OA] et de même longueur. Selon la classe, c’est un résultat bien connu sur l’orthogonalité, soit des droites soit des vecteurs. On peut aussi se placer en début de lycée, quand la propriété n’est pas nécessairement connue. Une démarche (attitude mathématique du socle commun) consiste alors à utiliser une lecture graphique dans un premier temps et à engager une interprétation algébrique de cette lecture. Cette interprétation algébrique peut même être un objectif d’induction du numérique vers l’algébrique, participant à se représenter le champ algébrique comme conceptualisation du champ numérique. Le script suivant peut alors se construire par étape :
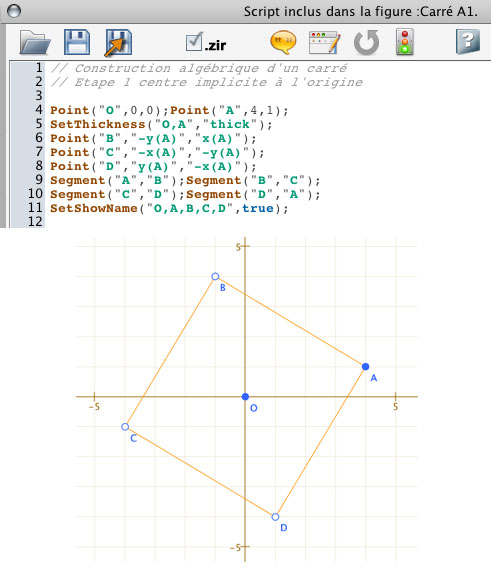
Pour écrire les coordonnées du point B (ligne 5) sans connaître le résultat, on peut envisager la démarche « d’investigation algébrique » suivante,désormais possible grâce à cet outil :
Attitude d’investigation en géométrie repérée
– entrer la ligne 4 comme seul contenu du script,
– l’exécuter,
– lire les coordonnées (-1,4) du point à construire,
– et conjecturer l’interprétation algébrique de la ligne 5.
– Puis annuler le script précédent, ajouter la ligne 5, exécuter le script
– ET valider par une manipulation directe du point A.
C’est la dernière ligne de cette séquence qui donne à la démarche proposée son statut d’investigation. En effet les coordonnées des points, données dans un script, ne fixent pas les points dans la figure, mais les initialisent seulement.
En faisant cette manipulation, l’élève peut déplacer A sur d’autres coordonnées entières pour non seulement valider l’orthogonalité de manière perceptive mais aussi valider que sa compréhension algébrique a bien été prise en compte dans le script comme on peut le penser.
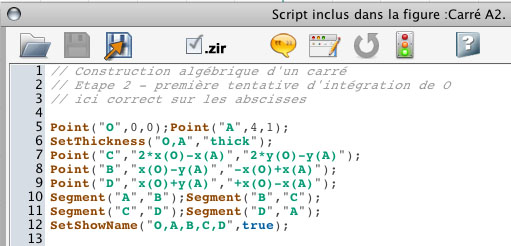
On notera que le point O ne sert pas, mais souvent les élèves placent le centre d’une figure avant de commencer. On vérifie par manipulation que le carré n’est pas véritablement de centre O mais bien implicitement de centre l’origine du repère. L’objectif suivant est alors de faire un authentique travail algébrique – éventuellement avec une fiche pour une trace dans l’environnement papier-crayon – non plus seulement pour explorer avec les scripts mais bien pour anticiper et produire les coordonnées correctes.
Géométrie repérée dynamique : travail algébrique validé par la manipulation directe
On a choisi depuis plusieurs années d’utiliser massivement le tableur comme outil d’intermédiation entre l’arithmétique et l’algèbre : le tableur a été retenu car il permet de travailler sur les variables sans pour autant faire de l’algèbre. D’un point de vue didactique, c’est de l’algèbre « sur des objets (1) », ces objets étant les cellules. On sait que le projet de ne pas quitter le tableur (pour certaines classes) fait que l’évolution vers l’algèbre ne se fera pas rapidement, mais ce n’est pas l’objectif des curicula de ces classes. Pour d’autres classes au contraire, l’utilisation du tableur est une étape qui accompagne le passage à l’algèbre par l’utilisation des cellules comme représentation des variables (avec un nom, un contenu, etc.).
La démarche que l’on propose ici, d’un travail algébrique sur la géométrie repérée avec validation par la géométrie dynamique à travers les scripts (2) se situe clairement plus du côté de l’algèbre que le tableur. Mais elle garde aussi cette dimension de « calcul sur les objets » car une fois le script exécuté, les élèves peuvent manipuler les points qu’ils ont eux-mêmes construits. La dimension algébrique est alors acceptée comme embarquée dans ce projet de travail sur les objets. Et par cette manipulation de la figure, avec les objets produits par leurs propres scripts les élèves acquièrent aussi (3) des connaissances algébriques.
(1) Au sens du « calcul sur les objets » des auteurs comme Brissiaud ou Ouzoulias dans leurs ouvrages pour l’école primaire : le passage par des objets (ici déjà conceptualisés) est un accélérateur de conceptualisation de ce que l’on veut enseigner. Le succès des méthodes Tchou et Picbille en est une conséquence. L’IREM de La Réunion a réalisé un film de 40 min sur les trois cycles de l’école primaire sur ce thème. On peut le télécharger dans cette page. Nous retrouvons le thème de la réification, appliquée à l’algébre : une forme de travail sur les scripts de CaRMetal permet une réification de l’algébre.
(2) qui peut se pratiquer d’abord individuellement puis ensuite plus régulièrement de manière collective au vidéo projecteur ou au TNI.
(3) Et il est facile, devant l’interaction langagière des élèves face à leurs productions à l’écran, de valider une nouvelle fois cette phrase lapidaire de/et que Gérard Vergnaud aime rappeler : « la connaissance opérationnelle est supérieure à la connaissance prédicative ».
On voit donc ici qu’un travail régulier sur ce type de scripts dans un environnement dynamique, outre qu’il est pleinement en accord avec les nouveaux programmes, s’inscrit dans une logique générale d’apprentissage qui a amené à inscrire le tableur dans de nombreux programmes, tout en restant dans une véritable démarche algébrique.
La situation n’est d’ailleurs pas simple pour les élèves. Ayant pris conscience de la non utilisation du point O dans le script précédent, on n’aboutit pas au carré algébrique en une seule étape, loin s’en faut. Parfois les élèves travaillent implicitement sur une seule coordonnée, sans même s’en apercevoir avant d’invalider leur travail par la manipulation des points de base.
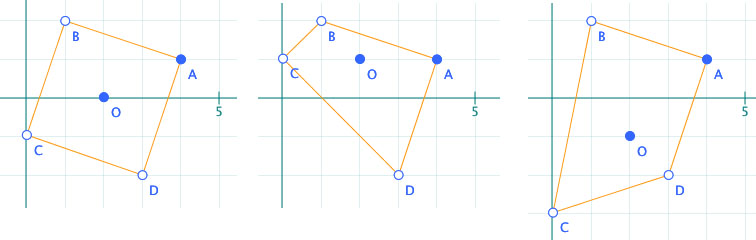
analyser ses erreurs et (éventuellement) avoir une aide à l’organisation des calculs …

On retiendra de ce paragraphe l’enjeu que peut avoir, pour une entrée efficace dans l’algèbre, la manipulation d’objets, produits par les élèves, issus de leurs propres raisonnements algébriques, et les possibilités – selon les élèves, les classes et le projet d’apprentissage - d’une phase que l’on a dite « d’investigation algébrique » pour aider à l’induction vers l’algèbre.
Sur un plan plus technique, on aura observé dans les scripts précédents combien l’écriture mathématique dans les CarScripts est proche de l’écriture mathématique au tableau : pour le moment, c’est la même , elle est seulement envoyée aux points de la figure par une expression entre guillemets – par une chaine de caractères donc. On aura bien compris qu’alors on n’envoie pas une initialisation comme quand on donne une valeur numérique, mais bien un calcul littéral. Voici par exemple les coordonnées du point B dans le logiciel :

Cela signifie aussi que, dans des classes ou l’algorithmique n’est pas au programme, la même démarche, mais simplement dans l’inspecteur d’objet, est aussi une pratique de géométrie repérée dynamique, elle aussi plus proche de l’algèbre que la pratique des tableurs.
L’inspecteur d’objet, comme les autres outils, a un fonctionnement a-modal y compris dans l’écriture algébrique : chaque écriture (même partielle) qui a un sens algébrique est automatiquement interprétée et la figure actualisée, ce qui facilite grandement l’investigation.
Interaction dynamique
Insertion de variables JavaScript dans les figures.
Exemples en analyse et statistique.
Les scripts précédents sont élémentaires au sens où ils sont écrits essentiellement du côté de la géométrie. Ils sont en fait des exercices plutôt de géométrie analytique – que de programmation – auto-validés par l’utilisation des scripts et la manipulation directe sur la figure produite.
Il y a donc, déjà, l’utilisation d’une interaction entre le JS et le logiciel puis qu’il y a transmission d’informations algébriques, mais ce n’est pas que ce type d’interaction que l’on peut attendre d’une intégration annoncée comme réussie. Qu’en est-il du passage des variables JS dans les figures de CaRMetal ?
Continuons notre exploration de la géométrie repérée dynamique en nous intéressant à la réalisation d’un tableau de fils dynamique.
Un préalable statique
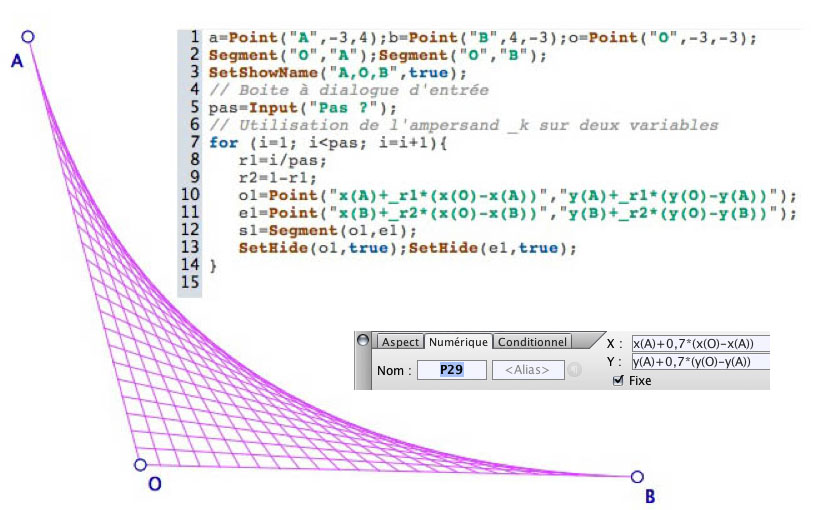
Cette activité suppose d’avoir fait au préalable, un tableau de fils statique, par exemple sur les coordonnées entières dans le cadre d’un apprentissage de la boucle for.
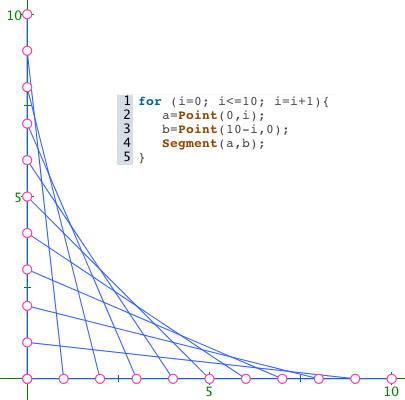
L’exemple ci-dessus est statique au sens où l’on peut déplacer les points indépendamment les uns des autres : l’utilisation de valeurs numériques initialisant les points, ceux-ci ne sont pas liés entre eux, on n’a fait qu’un dessin.

Fils dynamiques par boucle d’itération
Faire un tableau dynamique à partir par exemple de trois points A, O, B nécessite de partager les segments [OA] et [OB], de parcourir ce partage par une boucle et de construire des points associés. Il va donc falloir envoyer une variable javascript à CaRMetal qui a lui-même ses propres variables. La syntaxe est celle de l’adressage indirect des logiciels de programmations actuels : pour envoyer le contenu de la variable javascript k à CaRMetal, on utlise _k dans les coordonnées des points, comme dans ce script :
En lisant la ligne 1 du script, chacun remarquera que les segments [OA] et [OB] sont initialement orthogonaux. Sur l’illustration, les points ont été déplacés après le tracé du tableau de fils qui, parce qu’il est dynamique, devient en fait un tableau affine.
Remarques sur l’écriture :
– À part l’underscore _k le reste de l’écriture est conforme à ce que l’on pratique en classe.
– On remarque les coordonnées d’un des points : elles sont fonction de O et B, et du contenu de la variable k.
– Cette syntaxe vise à simplifier une écriture plus basique qui fonctionne toujours, celle par concaténation, mais de peu de lisibilité : « x(A)+ »+r1+« *(x(O—x(A)) ».
– Informatiquement, c’est bien un adressage indirect, d’où la notation. En classe on peut installer sans problème la représentation d’un passage d’une variable par contenu.
Ce passage par contenu - plutôt que par valeur comme c’est le cas ici - va être plus explicite dès l’activité suivante, quand la variable ne sera pas uniquement une valeur numérique mais une structure un peu plus complexe.
Une figure CaRMetal comme entrée d’un script : scripts génériques
Jusqu’ici nous avons travaillé sur des scripts qui produisaient des objets dans la figure. Nous allons voir qu’il est facile de réaliser des scripts génériques, qui s’appliquent à toutes les situations d’un même type, celles-ci étant considérées comme des entrées du script. Nous allons faire cela sur un thème du lycée qui va nous permettre en même temps d’aller un peu plus loin sur l’échange entre les variables JS et CaRMetal. La situation est la méthode d’Euler dans le contexte de la classe de 1°S comme primitivation approchée de fonction dont « on » (les élèves) ne connaît pas de primitive. Nous avons choisi de prendre la fonction proposée dans les documents d’accompagnement des programmes.
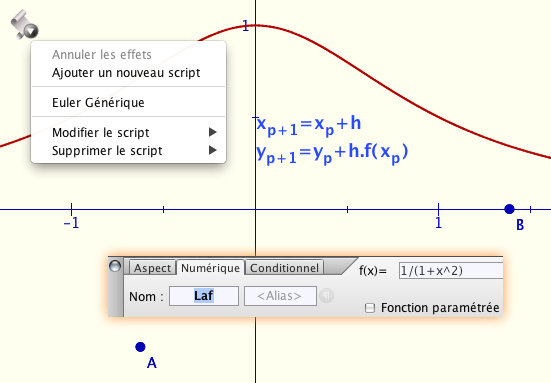
Le script est déjà contenu dans la figure. Du côté de la figure, il va s’appliquer à deux points A et B et une fonction Laf. Du côté du programme, celui-ci prend en compte ses valeurs d’entrée, A et B et Laf : la figure est une donnée du script pour son exécution.
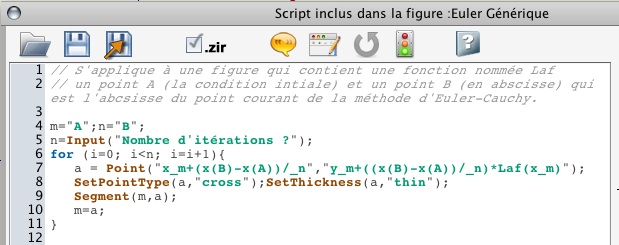
On notera l’écriture du pas avec A et B, pour que le résultat soit dynamique. Remarquons que ceci n’est pas propre au script : si on voulait faire la construction géométriquement, par macro, pour que la figure soit dynamique, il faudrait aussi prendre le pas en fonction de A et B. Ceci est bien détaillé dans cette vidéo très instructive de Monique Gironce.
Dans l’illustration suivante, en haut, l’application du script, à droite le changement de fonction, avec changement immédiat du résultat du script, puisqu’il est entièrement construit sur ses données initiales.
Sur la syntaxe simplifiée : cette fois on passe par contenu non plus des variables numériques, mais des points et plus précisément leurs coordonnées. Il aurait fallu écrire x(_m) mais l’auteur a introduit dans ce cas là, conformément à l’usage dans les langages de programmation actuels, la simplification syntaxique x_a et y_a pour x(_a) et y(_a), écritures qui restent fonctionnelles bien entendu. C’est pour cela que l’on garde l’expression passage par contenu plutôt qu’un traditionnel « par valeur ».
On trouvera, dans les classeurs en fin d’article d’autres utilisations en géométrie repérée, et en analyse, dans un contexte scolaire ou non (systèmes dynamiques de Hénon, ou du Gingerbread Man). Regardons maintenant du côté des statistiques.
Utilisation en statistique
C’est un domaine à la fois facile d’accès, pour lequel l’usage des scripts est pertinent, et qui peux être plus dynamique que ce que l’on fait d’habitude – le forum de CaRMetal sur les CarScripts contient surtout des propositions en statistique. On peut bien-sûr faire de simples programmes en « JS pur » avec une sortie texte, on est alors quasiment devant une calculatrice. La sortie graphique est quand même plus intéressante.
Voici quelques exemples de contributions générées par les échanges entre l’IREM de Toulouse et celui de La Réunion, disponibles en ligne. Tout d’abord les histogrammes sur les aires de rectangles inscrits dans un triangle.
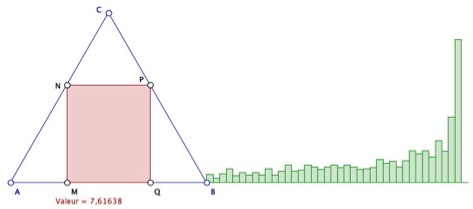
Le thème du parcours aléatoire est fort présent dans l’ingénierie scolaire. Ici il s’agit simplement de modéliser l’exercice « nombre de lancers d’un dé à 4 faces pour sortir du carré » et d’étudier statistiquement la situation. Le premier script fait, lentement, visible à l’œil, une partie, une par lancer du script. Le second fait 20 parties d’affilées pour des premiers résultats statistiques. L’habillage POV-Ray est dû à Alain Busser.
D’autres thèmes classiques peuvent être revisités d’une manière plus dynamique que ce qui est proposé habituellement aux élèves, c’est le cas par exemple du problème de la coïncidence des anniversaires dans une classe. Nous ne sommes plus dans le registre de la réalisation par les élèves mais dans la préparation de figures plus sophistiquées pour les enseignants.
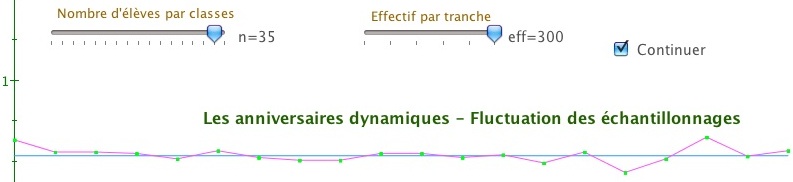
Dans l’illustration suivante, dans chacune des 20 tranches d’échantillons on effectue des tirages pour un effectif de classe donné, allant de 50 à 300 par pas de 50.
Dans le même temps – et toujours en temps réel – on peut choisir par classe les effectifs allant de 20 à 36 élèves. C’est bien entendu ce point là qui est nouveau par rapport aux autres pratiques : les scripts – et la manipulation aisée des booléens par le logiciel – permettent de mettre sur chaque point (comme une pile booléenne) les résultats pour tous les effectifs de classe, sous la forme d’une combinaison linéaire de booléens écrite par le script et mise à jour à chaque tirage (ci-dessous, l’ordonnée d’un point pour des échantillons de 50, pris en cours d’exécution du script) :
(n==20)*23/50+(n==21)*24/50+(n==22)*26/50+(n==23)*27/50+(n==24)*30/50+(n==25)*33/50+(n==26)*34/50+(n==27)*35/50+(n==28)*36/50+(n==29)*36/50+(n==30)*37/50+(n==31)*38/50+(n==32)*39/50+(n==33)*39/50+(n==34)*39/50+(n==35)*42/50+(n==36)*43/50
Le balayage du nombre d’élèves par classe au curseur ne fait que donner à cette expression la valeur correspondante. Le point est alors affiché en temps réel, toutes les données étant déjà dans ses coordonnées.
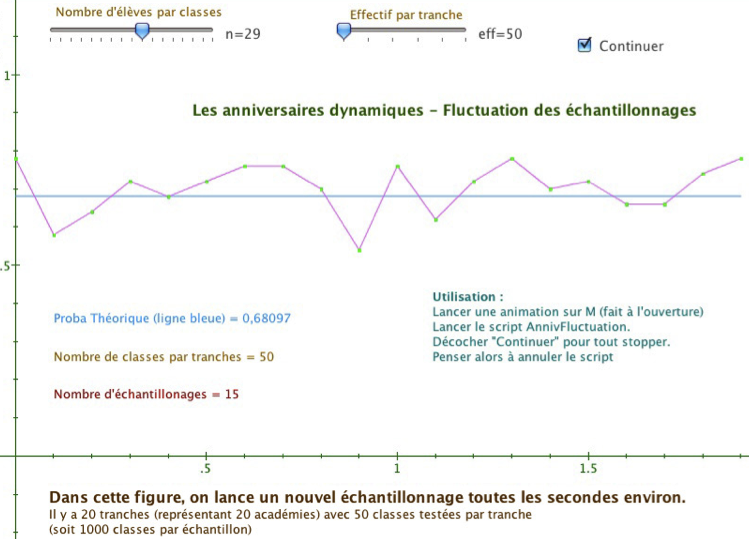
On peut tout de suite observer l’effet des effectifs sur la fluctuation des échantillonnages et le positionnement autour de la valeur théorique.
Le script de cette figure (relativement complexe pour avoir le maximum de réactivité dynamique) est étudié dans cet article (dont le premier onglet, sur les 8 reines de l’échiquier a déjà été abordé dans l’onglet sur les booléens)
De nombreux autres scripts bien plus élémentaires et tout aussi pertinents (toile Web, statistique) sont disponibles dans les classeurs proposés en téléchargement et en utilisation en ligne.
Statique/Absolu
Un subtil mélange de statut
Nous poursuivons notre réflexion sur la géométrie repére dynamique initiée au premier onglet. Nous essayons de préciser en quoi l’usage des scripts sur de simples exercices de géométrie analytique peut-il enrichir les représentations des élèves, aussi bien dans le champs géométrique, algébrique ou celui de la programmation, voire de l’algorithmique.
Ici nous allons ajouter un peu de géométrie à la démarche analytique mais le propos essentiel reste centré sur les représentations liée à la géométrie repérée. Le matériel de base va être le cercle trigonométrique, et l’enjeu sera la perception du statique et du dynamique qu’il y a dans les scripts que l’on va écrire. On pourrait croire que c’est une problématique - et une expertise - de géométrie dynamique, mais en réalité, comme nous l’avons vu au premier onglet, la géométrie dynamique va nous servir, du côté de l’élève, d’outil d’auto-validation pour nous interroger et faire progresser « nos » représentations de la programmation, voire éventuellement de l’algorithmique.
Plusieurs ingénieries peuvent être construites par les enseignants avec les scripts proposés ici, selon le niveau de la classe, la pratique de la programmation. Plutôt que d’en proposer une, qu’il serait nécessaire de modifier et d’adapter, nous proposons plutôt des pistes de réflexion pour que chacun construise ses propres séquences : la pédagogie est elle aussi un micromonde où chacun doit tout faire, mais c’est aussi pour cela que nous aimons notre métier.
Analyse d’un script
Commençons par ce script, éventuellement que l’on propose à l’analyse en classe puisque c’est une des compétences à travailler, sur les trois niveaux du lycée. Et ici, c’est bien dans l’analyse que le discours va être intéressant, que les représentations sur les implicites des repères (et les repères implicites) vont devoir s’exprimer.
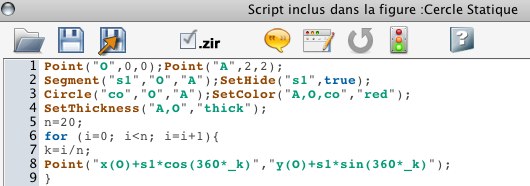
Clairement ce script construit un cercle de centre O passant par A (points gras) et sur ce cercle place 20 points. Divers commentaires techniques peuvent être possibles, en particulier on notera que l’on a construit le segment [OA], en lui donnant un nom dans CaRMetal, s1 ce qui permet d’utiliser s1 comme mesure pour le rayon du cercle dans la ligne 8 et éviter un calcul de distance. On peut aussi parler de la référence explicite au point O, et donc de la dépendance du cercle à ce point, ce que l’on voit ci-dessous (on a déplacé seulement le centre).

Pendant le déplacement de O, les plus curieux peuvent de se poser des questions sur le mouvement des autres points. Ils paraissent, à réduction prés du cercle, se déplacer en translation. Qu’en est-il en fait ?
Avant de déplacer le point A, et pour voir le mouvement des points, on peut en colorier quelques uns, ce qui donne :

Manifestement les points, s’ils se déplacent à l’écran quand on manipule O ou A, restent figés sur le cercle de centre O, ils ne se déplacent pas sur ce cercle. Ces points, construits géométriquement, conservent un comportement statique sur le cercle. Selon la classe, selon si c’est une évidence ou pas, un questionnement sur ce sujet peux être lancé. La raison en est évidemment élémentaire, et on peut voir sur les coordonnées des points que les angles utilisés sont absolus :

Mais pour avoir fait plusieurs formations sur les CarScripts, on voit qu’ici la représentation que l’on a du dynamique est questionnée. Elle l’est déjà sur l’articulation entre le statique et l’absolu. En effet, jusqu’ici le statique était identifié au dessin que la manipulation directe cassait (les tableaux de fils statiques) alors qu’ici l’absolu, s’il contient une dimension statique, s’inscrit aussi dans une logique dynamique. Elle l’est d’autant que, dans de nombreuses situations, l’usage des angles absolus peut suffire. Voyons en un exemple.
Un absolu pas si statique qu’on pourrait le penser
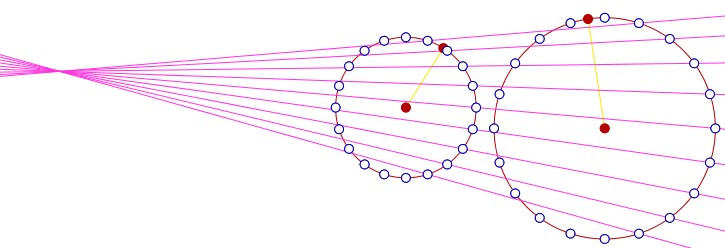
En fait le script précédent est une partie de script. La figure originale, utilisée en formation, était la construction d’une néphroïde comme enveloppe de cercles. On se donne un cercle de diamètre [AB] et à partir d’un point M du cercle (les points du script précédent) on construit le cercle de centre M tangent à [AB]. On obtient alors une néphroïde. Si on s’arrange pour la construire à partir de deux points, le centre O du cercle et un point A qui définit ce cercle, elle est manipulable facilement. Et elle fait totalement illusion - au sens où l’on oublie l’aspect absolu des angles - car en manipulant A, même avec ces angles absolus, le cercle de centre un point donné bouge avec A puisque le diamètre [AB] bouge aussi.

Mais si, dans un contexte géométrique donné, on devait répondre à une contrainte dynamique spécifique, comme utiliser un cercle particulier en fonction de A - le 4° cercle avant le point A dans l’illustration ci-dessous - clairement la figure ne convient pas, c’est-à-dire l’algorithme ne convient pas, les angles absolus ne suffisent plus.
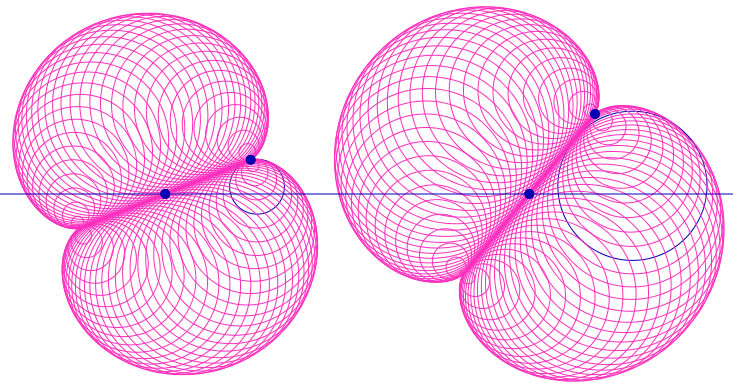

Une version scolaire du questionnement absolu/statique
L’exemple précédent a été proposé pour mettre en valeur la subtile relation entre statique/absolu/dynamique : la frontière, dans cet exemple la, n’est pas si claire que cela. Cela dépend de l’usage que l’on fera de la figure. En classe, pour provoquer ce questionnement, il est préférable d’utiliser une situation sans ambiguïté. On se place dans un contexte où l’on n’a pas abordé la question du script introductif de cet onglet, pour découvrir la problématique avec cet exemple.
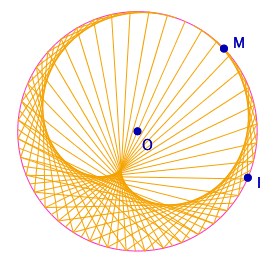
Il s’agit cette fois de faire une cardioide par enveloppe de segments : on place sur le cercle n points avec un angle au centre constant entre deux points consécutifs et, en parcourant deux fois le cercle, on joint les points d’indice k et 2k.

avec ce script ...

... c’est clair qu’en déplaçant A, la cardioïde ne va pas suivre. Et pourtant ... c’est souvent une surprise, et c’est elle qui fait surgir la question de l’angle absolu et fait ressortir des représentations de cette situation, soit sur les angles, soit tout simplement sur les nombres réels car après tout, utilise-t-on des angles ou des réels ici ?
C’est l’occasion de revenir sur l’interrogation initiale de notre représentation du dynamique. Elle est aussi imprégnée de cette question de la relation aux nombres. On a envie de dire tout simplement(*) : le statique est du registre numérique, le dynamique du registre algébrique. S’il y a confusion, elle vient assez généralement de ce qu’on a transmis une partie des données algébriquement et d’autres numériquement comme on le voit bien sur l’illustration des coordonnées des points.
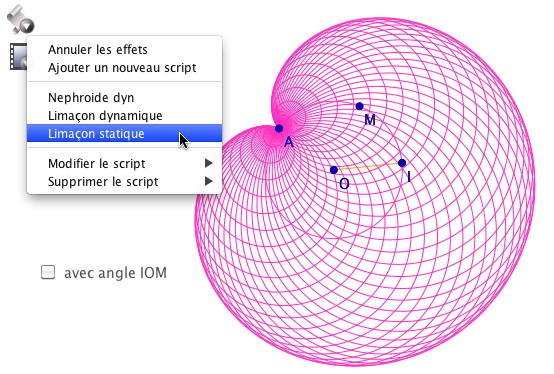
Pour éclaircir cela on peut proposer aux élèves la contrainte suivante : faire que la cardioïde construite par des segments suive le point A, plus précisément qu’elle soit de « sommet » le point A. Il n’y a pas grand chose à modifier bien entendu mais cela peut être complexe pour les élèves car, pour faire cela, il est plus simple de se placer dans un autre contexte (que l’on peut préciser), celui où les objets sont déjà sur la figure.
On se donne donc un cercle de centre O passant par I, un point M sur objet du cercle. On note ang, l’angle IOA. De fait, on s’est donné une origine des angles. Il faut (inspecteur d’objet) donner à la mesure de ang une amplitude jusqu’à 360°.

ce qui donne bien ce qui est attendu
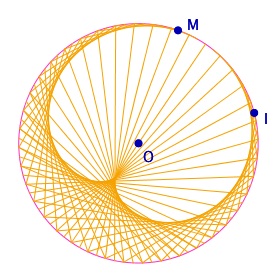
En particulier une animation sur M produit bien l’effet souhaité d’une rotation de la cardioïde.
<br clear = all)
Une version booléenne est disponible au téléchargement : la cardioïde suit M seulement si la case est cochée.
Puisque l’on a réalisé l’animation de la cardioïde avec le point M comme sommet, et que nous savons enrouler les tours sur le cercle - onglet Temps1 de la partie 1 - serait-il possible de faire, par script, une cardioïde dynamique temporelle ? La réponse est bien-sûr oui, et la mise en œuvre est dans la galerie ...
Bilan de l’onglet : premières pratiques de trigonométrie dynamique ?
Dans un registre différent de la (simple) géométrie repérée dynamique, plus délicat en terme de concepts mathématiques engagés (le cercle trigonométrique et la mesure des angles), nous commençons à dégager cet invariant que l’interaction entre la géométrie dynamique et la programmation, par la manipulation directe sur les objets produits, permet d’enrichir les deux cadres de travail.
A travers des problèmes concrets (on travaille sur des objets, produits par les élèves), on manipule les outils usuels de la géométrie analytique élémentaire et de la trigonométrie en se posant des questions contemporaines (manipulation directe d’image) tout en revisitant, de manière originale les concepts mathématiques engagés.
(*) Même si on se doute que c’est moins simple : un point au tiers d’un segment est du registre numérique. Mais parce que la manipulation directe respecte les relations affines, elle lui donne aussi, dans ce contexte de point sur objet, un statut dynamique.
Galerie
Galerie de scripts
Le site de l’IREM de La Réunion comportant déjà de nombreuses pages sur les scripts (dont les ateliers de TP de seconde de Alain Busser, voir les liens en fin d’article), le lecteur intéressé à poursuivre est invité à explorer les pages du site, en allant dans les rubriques dédiées. Nous poursuivons maintenant par quelques exemples de scripts produits hors considérations scolaires, que l’on peut s’amuser à réaliser, pour tester les capacités du logiciel et le degré d’interaction entre le langage de script et la géométrie dynamique.
La même technique de la pile indiquée à la fin du deuxième onglet – qui tient en quelques lignes de code - peut être appliquée à de très nombreuses situations. La figure suivante a été faite sur le même principe, avant que la version 3.5 ne soit finalisée – et en particulier avant que l’outil Conditional qui permet de placer les segments cachés en pointillé(*) soit disponible. En présentation, on fait le choix de colorier, devant l’auditoire, deux segments pour que l’on voit bien que ce sont des segments uniques qui sont construits (et non pas des segments différents pour chaque valeur de n du curseur), et qu’ils sont eux aussi balayés par une pile en fonction du découpage donné par le curseur.

(*) Voir le manuel de référence de Alain Busser, page 65 pour une autre sphère avec des pointillés.
Terminons cette présentation par deux beaux scripts qui montrent l’extraordinaire intégration réalisée au sein de ce logiciel entre le JavaScript et les outils internes à CaRMetal.
La récursivité dynamique (sur la courbe de Cesaro)



Dans la figure C est le transformé de A de centre B dans la rotation d’angle π-2rot.
Animation – Script et temporalité
Nous terminons cette micro galerie de scripts par un retour à la question de la temporalité dans les figures. Qu’en est-il des scripts et de la gestion du temps ? La nouvelle animation de la version 3.5 est-elle capable de respecter cette temporalité ?
Pour observer cela, nous poursuivons sur la cardioïde par segments déjà rendue dynamique dans un onglet précédent. Les plus anciens se souviendrons peut-être des « bolygones » du début des TO7 et MO5 … quel recyclage ! Pour rester dans ce siècle ci, on va y ajouter d’une part, un pas variable en temps réel (ie il y aura de 60 à 120 segments) mais surtout une rotation de la cardioïde qui pourra prendre trois aspects : standard, temporel discret, temporel continu.

On a utilisé la macro-construction « Curseur circulaire » pour construire M : c’est un point qui s’enroule sur le cercle avec son compte tours. La macro renvoie l’angle absolu et le nombre de tours. Les pop-up menu et le curseur ne sont pas actifs, ce sont des données qui seront utilisées par le script suivant :
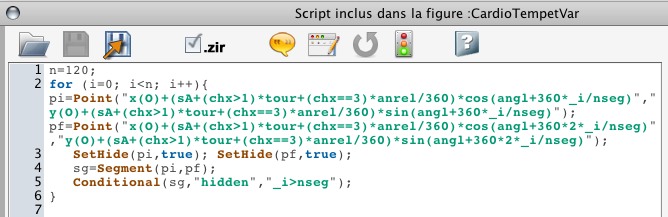
Le script construit le segment [pi pf]. L’écriture paraît complexe mais c’est seulement parce que le rayon du cercle est un peu long à écrire et qu’il est utilisé 4 fois.
sA est le rayon du cercle initial, nseg est le nombre de segments, donné par le curseur. On remarquera que la boucle va jusqu’à 120, tous les segments sont construits, même si nseg est plus petit. Leur affichage est traité dans la ligne 5, la dernière ligne de la boucle, le segment est caché si son indice est trop élevé. Ainsi les points ne sont calculés qu’une fois, seul leur affichage dépend du curseur.
La variable chx est bien sûr le choix du popup. Le rayon du cercle par défaut vaut sA. On lui ajoute une expression si chx>1 (donc si on fait un choix de cardioïde temporelle). Dans ce cas on lui ajoute le nombre de tours, c’est le sens de (chx>1)*tour. Si de plus on a fait le choix temporelle continue, il faut ajouter une variation continue du rayon : c’est l’expression (chx==3)*anrel/360.
On remarquera aussi l’économie considérable du traitement par les booléens qui évitent le recours à des conditionnels imbriqués qui seraient difficile à mettre en œuvre dans ce cas.
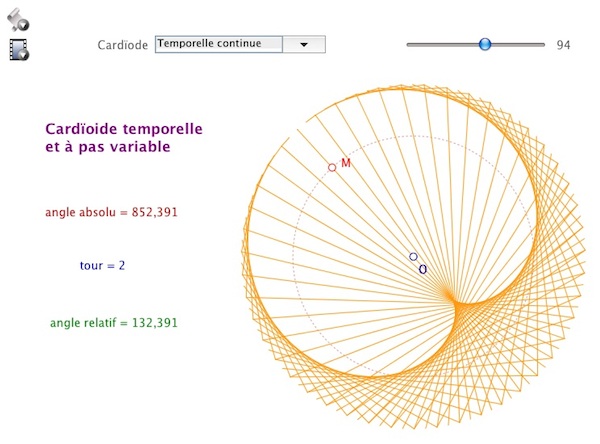
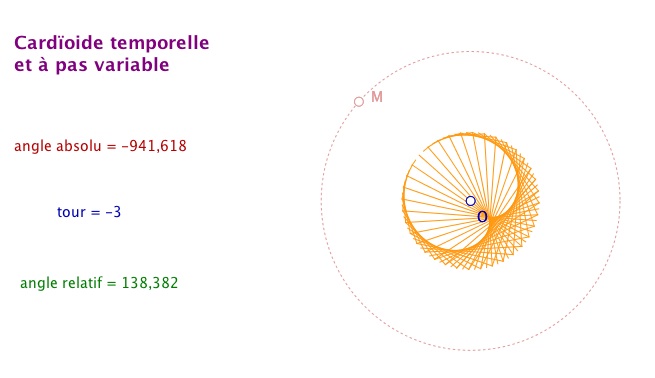
Bien entendu, pendant l’animation, on peut faire sauter la cardioïde d’un mode à l’autre en changeant de choix dans le pop up et faire varier le nombre de segments.
Une dernière expérience illustrera, une nouvelle fois, la profondeur de l’intégration des outils entre eux. Si avant de lancer l’animation sur M, on fait faire 3 tours en arrière à M, en mode temporel et qu’on lance l’animation, celle-ci démarre bien dans l’état temporel de la cardioïde. On peut en conclure que l’animation de CaRMetal respecte la temporalité et le déterminisme enrichi induit.
Ressources
Site de CaRMetal : Téléchargement, nombreux tutoriels en flash, diaporamas dynamiques (collège), galerie des utilisateurs, forums.
Nouveautés de la version 3.5 (avril 2010, avec un classeur d’exemple).
Dont l’utilisation de l’outil Monkey.
Un interview de Éric Hakenholz sur Framablog (octobre 2009)
Sur les scripts
L’IREM de la Réunion a un groupe algorithmique avec les CaRScripts qui propose un manuel de référence de 67 pages (Alain Busser), des articles de prise en main pour l’enseignant, et de propositions d’utilisations dans lesquels les exemples vus ici sont repris et largement détaillés, avec plusieurs dizaines de scripts. On trouvera aussi deux rubriques très fournies de Alain Busser :
– Narration de recherche sur les TP d’algorithmique en classe de seconde.
– Une rubrique Sujets de l’épreuve pratique TS 2009 avec de nombreux scripts.
Prise en main des CarScripts (dont PDF) | Itération 1 | Itération 2 | Espace (plus technique)
Le groupe de travail Abaques et nomogrammes utilise les CaRScripts. Les scripts sont essentiellement dans les 4 sous-rubriques.
Classeurs de cet article
Les classeurs proposés sont bien plus riches que les quelques exemples exposés ici. En particuliers, ils reprennent les scripts de plusieurs articles précédents sur les CaRScripts tout en s’inscrivant dans une logique d’utilisation adaptée à la nouvelle organisation sous forme de classeurs (lire les commentaires des figures).
Classeurs de cet article en ligne
Par rapport aux fichiers précédents, on a fixé le nombre d’itération (pour éviter la fenêtre surgissant de l’input) qu’on peut modifier en éditant le script. Le script sur le robot n’est pas présent en ligne, le déplacement successif de l’image du robot en ligne n’est pas stable quand on relance le script (pour le moment). Les figures n’étant pas redimensionnables, elles sont plus petites pour s’adapter à tout écran.
Il y a plus de 50 scripts en ligne répartis sur 5 classeurs.
Utilisation plus générale de CaRMetal sur le site de l’IREM



Commentaires