Principe de base pour placer des points dans l’espace

Quand les personnes chargées du débuggage des premières versions se sont penchées sur les scripts pour l’espace, dans un premier temps nous pensions qu’il fallait passer les différends paramètres du trièdre au script et nous trouvions cela compliqué.

C’est Jérôme Caré régulièrement présent sur les forums de CaRMetal qui a eu l’idée d’utiliser directement les points du repère, sachant qu’un point $M(x_M,y_M,z_M)$ dans le repère (O, X, Y, Z) de la feuille d’espace est représenté par le point du plan de la figure $M_e(x_O+x_M(x_X-x_O)+y_M(x_Y-x_O)+z_M(x_Z-x_O),y_O+x_M(y_X-y_O)+y_M(y_Y-y_O)+z_M(y_Z-y_O))$

En effet pour que le minimum de l’exigence du « contrat statique » fonctionne, il faut, dans les points construits, faire explicitement référence aux points O, X, Y, Z, toute variable intermédiaire rendrait la figure en dessous de cette exigence (ie elle serait réellement statique à l’écran comme chacun peu le tester). En suite les coordonnées sont passée par contenu, d’abord par valeur numérique comme ci-dessous, puis avec différents paramètres quand le contenu sera plus complexe.

Ainsi pour placer un point dans les figures d’espace de CaRMetal, on peut utiliser tout simplement cette fonction générique :

Comme c’est une première utilisation des fonctions utilisateurs dans les Carscripts, on notera qu’il faut recopier les paramètres (et ne pas les passer en variable locale par un var, c’est pour cela qu’on leur a donné un nom à deux lettres)

Exemple d’utilisation statique : la construction de l’icosaèdre

Le script suivant se lance sur une figure de l’espace blanche (avec le repère). Une pause de 7 s après la construction des 12 sommets de l’icosaèdre permet de manipuler cette figure par le traditionnel clic-droit glisser :

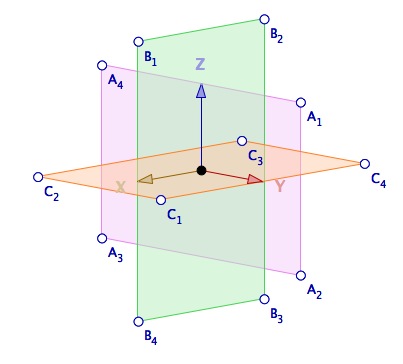
En fait tant qu’on ne relâche pas la souris la suite du script ne se réalise pas. Puis le script cache les trois plans et trace 12 des 20 faces de l’icosaèdre. Le scrpit est minimaliste pour sa deuxième partie : on prendra soin de cocher le remplissage des polygones et de choisir une couleur pour obtenir quelque chose comme :

// Construction  de l'icosaèdre

phi=(1+Math.sqrt(5))/2;

function TracePoint(Nom,ux,uy,uz){
vx=ux;vy=uy;vz=uz;	up=Point(Nom,"x(O)+(x(X)-x(O))*_vx+(x(Y)-x(O))*_vy+(x(Z)-x(O))*_vz","y(O)+(y(X)-y(O))*_vx+(y(Y)-y(O))*_vy+(y(Z)-y(O))*_vz");
}

//Tracé et nommage des 12 sommets
// Tracé des plans associés

Shownames();
TracePoint("A1",0,phi,1);TracePoint("A2",0,phi,-1);
a3=Symmetry("A3","O","A1");a4=Symmetry("A4","O","A2");
f=Polygon("A1,A2,A3,A4");
SetRGBColor(f,232,134,241);SetFilled(f,true);
SetThickness(f,"normal");Show(f,true);

TracePoint("B1",1,0,phi);TracePoint("B2",-1,0,phi);
b3=Symmetry("B3","O","B1");b4=Symmetry("B4","O","B2");
g=Polygon("B1,B2,B3,B4");
SetRGBColor(g,72,211,85);SetFilled(f,true);
SetThickness(g,"normal");Show(g,true);

TracePoint("C1",phi,1,0);TracePoint("C2",phi,-1,0);
c3=Symmetry("C3","O","C1");c4=Symmetry("C4","O","C2");
h=Polygon("C1,C2,C3,C4");
SetRGBColor(h,255,128,36);SetFilled(h,true);
SetThickness(h,"normal");Show(h,true);

// 7 s de pause pour manipuler la figure
Pause(7000);SetHide("_f,_g,_h",true);

// 12 des 20 faces de l'icosaèdre
f1=Polygon("A1,A2,C1");f2=Polygon("A1,A2,C4");
f3=Polygon("A3,A4,C2");f4=Polygon("A3,A4,C3");
f5=Polygon("B1,B2,A1");f6=Polygon("B1,B2,A4");
f7=Polygon("B3,B4,A2");f8=Polygon("B3,B4,A3");
f9=Polygon("C1,C2,B1");f10=Polygon("C1,C2,B4");
f11=Polygon("C3,C4,B2");f12=Polygon("C3,C4,B3");

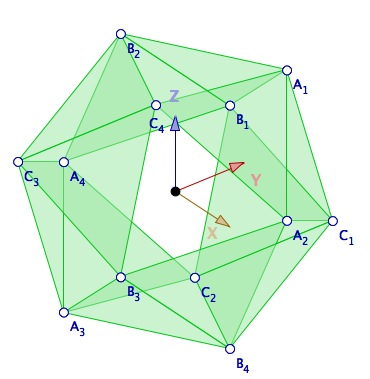
Remarque : il semble que les points construits par la fonction TracePoint échappent à la commande shownames(). Pas compris pourquoi, mais à étudier.

Il est alors intéressant de reprendre le polycopié de Alain Busser de la rubrique parente à cet article et de s’intéresser à sa sphère en trapèze, superbe à la fin du PDF.

On notera son utilisation de round : en effet, javascript pour des petits nombres, produit de écritures en 1 e-12 par exemple qui - pour le moment - ne sont pas interprétées par le logiciel qui ne connaît que le 1E-12 pour ce genre de situation. Ceci sera corrigé dans une prochaine version.

2. Premiers pas vers une figure d’espace dynamique

Dans ce deuxième onglet, nous allons aborder la situation intermédiaire, celle où l’on utilise des curseurs pour manipuler des structures. D’où l’idée de travailler sur un tore. Nous allons toutefois commencer par un tore statique, pour placer une méthodologie de construction.

2.a. Le tore en javascript

Dans cette première construction, nous allons construire d’abord les cercles méridiens, puis les cercles parallèles.

Pour cela nous allons construire des coniques par 5 points de manière automatique, en particulier en indexant les noms des points utilisés pour ces coniques. Voici le script pour les seuls cercles méridiens

On calcule donc les coordonnées de 5 points (j=1 à 5) d’un cercle méridien (pour i fixé), on nomme ces points « A »+j+i : le faible typage de javascript transforme cela en les points A11 à A517 ce qui permet de définir explicitement la conique qd1 par le nom des points qui la compose. On aurait pu procéder autrement, cela aurait été plus long.

Ce qui donne cela

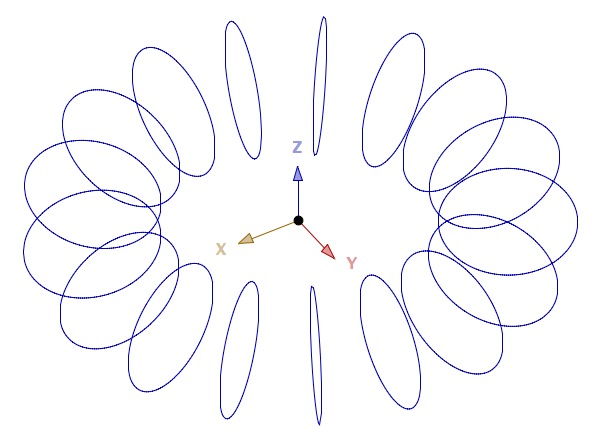
qui sans être fabuleux, est quand même fait au moindre coût.

Ajoutons des cercles parallèles

// Tore par cercle en rotation autour de l'axe (OZ)
// version statique, en JS à comparer avec une version dynamique
// le petit cercle de rayon Ri a son centre sur le cercle de rayon Re

Re=3;Ri=1;
n=17;
for (i=0; i<n; i++){
	t=2*i*Math.PI/n;
	for (j=1; j<6; j++){
		x=(Re+Ri*Math.cos(j))*Math.cos(t);
		y=(Re+Ri*Math.cos(j))*Math.sin(t);
		z=Ri*Math.sin(j)

		g=Point("A"+j+i,"x(O)+_x*(x(X)-x(O))+_y*(x(Y)-x(O))+_z*(x(Z)-x(O))",
		"y(O)+_x*(y(X)-y(O))+_y*(y(Y)-y(O))+_z*(y(Z)-y(O))");
		SetHide(g,true);
		qd1=Quadric("A1"+i,"A2"+i,"A3"+i,"A4"+i,"A5"+i);
		SetColor(qd1,"blue");
	}
}

// Les cercles paralléles à (XOY)

p=Math.round(n/2); // on prend approximativement la moitié
for (i=0; i<n; i++){ // on copie colle ce qui précède
	t=2*i*Math.PI/n;
	for (j=1; j<6; j++){
		x=(Re+Ri*Math.cos(t))*Math.cos(j); // on inverse juste j et t
		y=(Re+Ri*Math.cos(t))*Math.sin(j); // dans les 3 coordonnées
		z=Ri*Math.sin(t) // Attention à changer "A" en "B" dans Point

		g2=Point("B"+j+i,"x(O)+_x*(x(X)-x(O))+_y*(x(Y)-x(O))+_z*(x(Z)-x(O))",
		"y(O)+_x*(y(X)-y(O))+_y*(y(Y)-y(O))+_z*(y(Z)-y(O))");
		SetHide(g2,true);
		qd2=Quadric("B1"+i,"B2"+i,"B3"+i,"B4"+i,"B5"+i); // et ici aussi
		SetColor(qd2,"red");
	}
}

Ce qui produit ce tore « statique » au sens où il est juste manipulable par l’action sur le trièdre 3D de CaRMetal.

et qui en plus n’est même pas joli ... mais à cause des couleurs probablement

2.b Version dynamique, ajouts de curseurs

On peut ajouter deux curseurs pour les deux rayons, ce qui ne change pas fondamentalement le principe du script, on a déjà vu comment passer d’une version statique à une version dynamique. On n’oubliera pas que, pour CaRMetal, il faut utiliser les fonction trigonométriques rsin et rcos pour traiter des angles en radians. En pratique, si on cherche à écrire le script tout seul, on travaillera avec des curseurs d’expression, sinon on peut utiliser des curseurs systèmes. Dans les deux cas ils s’appellent Re et Ri. Là encore n doit être impair pour la raison évoquée dans la remarque précédente. Le script a été condensé dans une seule boucle.

//Tore dynamique avec Re et Ri curseurs

n=23;
for (i=0; i<n; i++){
	t=2*i*Math.PI/n;
	for (j=1; j<6; j++){
	g1=Point("A"+j+i,"x(O)+(Re+Ri*rcos(_j))*rcos(_t)*(x(X)-x(O))+(Re+Ri*rcos(_j))*rsin(_t)*(x(Y)-x(O))+Ri*rsin(_j)*(x(Z)-x(O))",
"y(O)+(Re+Ri*rcos(_j))*rcos(_t)*(y(X)-y(O))+(Re+Ri*rcos(_j))*rsin(_t)*(y(Y)-y(O))+Ri*rsin(_j)*(y(Z)-y(O))");
	SetHide(g1,true);
	qd1=Quadric("A1"+i,"A2"+i,"A3"+i,"A4"+i,"A5"+i);
	SetRGBColor(qd1,250-5*i,60+3*i,120+5*i);
		
// on utilise le même procédé (t<->j) dans une seule boucle

g2=Point("B"+j+i,"x(O)+(Re+Ri*rcos(_t))*rcos(_j)*(x(X)-x(O))+(Re+Ri*rcos(_t))*rsin(_j)*(x(Y)-x(O))+Ri*rsin(_t)*(x(Z)-x(O))",
"y(O)+(Re+Ri*rcos(_t))*rcos(_j)*(y(X)-y(O))+(Re+Ri*rcos(_t))*rsin(_j)*(y(Y)-y(O))+Ri*rsin(_t)*(y(Z)-y(O))");
SetHide(g2,true);
qd2=Quadric("B1"+i,"B2"+i,"B3"+i,"B4"+i,"B5"+i);
SetRGBColor(qd2,5*i,255-7*i,6*i)
	}
}

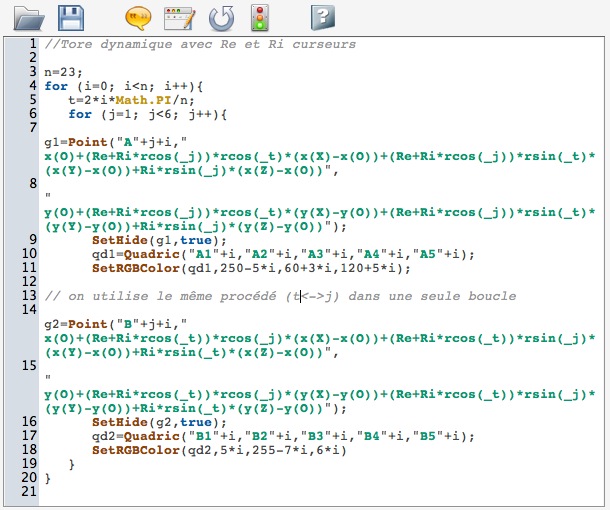
Sur lequel on voit qu’on peut grandement améliorer la colorisation ;-)

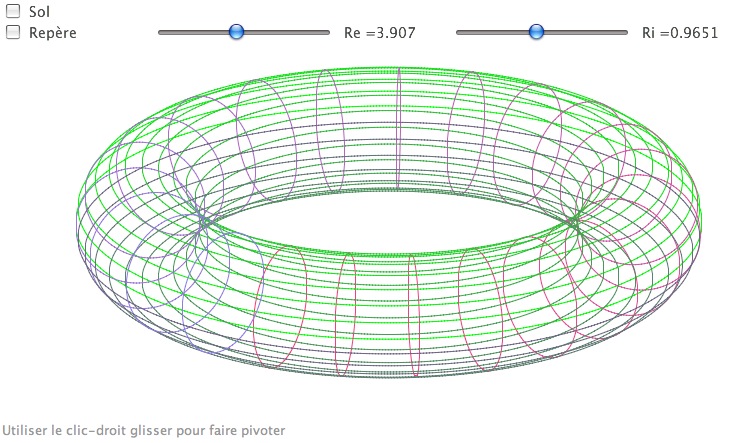
Il est toujours intéressant de voir comment est interprété le message transmis à CarMetal pour les coordonnées : on voit ici que rsin(2) est conservé tel quel : la chaine de caractère est envoyée à CaRMetal tant qu’elle est interprétable.

2.c Par les cercles de Villarceau

Mais au lieu d’engendrer le tore par deux familles de cercles, on peut choisir d’utiliser les cercles de Villarceau (mais aussi ici pour l’animation) dans une rotation autour de (OZ). On ne construit plus alors qu’une seule famille de cercles :

// Construction du tore par les cercles de Villarceau
// Ici 40 cercles de l'un des deux types

n=40;
for (i=0; i<n; i++){
	t0=2*i*Math.PI/n;
	for (j=1; j<6; j++){
		g=Point("A"+j+i,"x(O)+(-sqrt(Re*Re-Ri*Ri)*rcos(_t0)*rsin(_j)-(Ri+Re*rcos(_j))*rsin(_t0))*(x(X)-x(O))+(-sqrt(Re*Re-Ri*Ri)*rsin(_t0)*rsin(_j)+(Ri+Re*rcos(_j))*rcos(_t0))*(x(Y)-x(O))+Ri*rsin(_j)*(x(Z)-x(O))",
		"y(O)+(-sqrt(Re*Re-Ri*Ri)*rcos(_t0)*rsin(_j)-(Ri+Re*rcos(_j))*rsin(_t0))*(y(X)-y(O))+(-sqrt(Re*Re-Ri*Ri)*rsin(_t0)*rsin(_j)+(Ri+Re*rcos(_j))*rcos(_t0))*(y(Y)-y(O))+Ri*rsin(_j)*(y(Z)-y(O))");
		SetHide(g,true);
		t=Quadric("Qd"+i,"A1"+i,"A2"+i,"A3"+i,"A4"+i,"A5"+i);
	}
}

Ce qui est autrement plus esthétique

Dans le prochain onglet nous allons ajouter la construction d’un cercle de Villarceau dynamique sur la figure.

3. Prise en compte dynamique dans un carscript d’un point de l’espace

On veut maintenant ajouter une dimension dynamique dans la figure précédente. Bien sûr on n’a pas - pas encore ;-) - accés à la vraie 3D dans CaRMetal donc il faut - par exemple - avoir une relation linéaire entre les coordonnées (en particulier être dans un plan). C’est plus simple à traiter avec un point sur l’un des trois plans du trèdre de référence, aussi va-t-on prendre un point sur un cercle dans le plan (XOY) et construire le cercle de Villarceau associé.

Pour cela if faut récupérer les coordonnées 2D dans le plan (XOY) du point M. Dans ce cas, il serait trés simple d’utiliser un parallélisme aux axes et d’utiliser des points intermédiaires pour déterminer ces coordonnées.

Mais pour montrer que la démarche peut être plus générale, exprimons les corrdonnées planes $(x_p,y_p)$ d’un point M du plan du sol dont on a les simples coordonnées $(x_M,y_M)$ dans le plan de la feuille. Il s’agit de résoudre un système de deux équations à deux inconnues, et ces coordonnées sont, dans une notation utilisant les fonctions de CaRMetal x et y :

$x_p$ = $\frac{((y(M)-y(O))(x(Y)-x(O))-(x(M)-x(O))(y(Y)-y(O))}{(x(Y)-x(O))(y(X)-y(O))-(x(X)-x(O))(y(Y)-y(O))}$

$y_p$ = $\frac{(-(y(M)-y(O))(x(X)-x(O))+(x(M)-x(O))(y(X)-y(O))}{(y(X)-x(O))(y(X)-y(O))-(x(X)-x(O))(y(Y)-y(O))}$

On téléchargera la figure « Pour Villarceau Mobile ». Dans cette figure on dispose d’un point M sur le cercle de centre O de rayon Re. On va lui appliquer le script suivant puis celui précédent du tore (ou l’inverse). Ce premier script permet de piloter un cercle de Villarceau à partir du point M.

Pour réaliser facilement des figures 3D dans le plan du sol, un package de macros est disponible dans la dernière figure de ce diaporama.

// Ce script ajoute un cercle de Villarceau manipulable à la souris
// à partir d'un point M pris sur le cercle de rayon Re du plan du sol

//m2d est le point en 2D dans le plan (XOY)

m2d=Point("((y(M)-y(O))*(x(Y)-x(O))-(x(M)-x(O))*(y(Y)-y(O)))/((x(Y)-x(O))*(y(X)-y(O))-(x(X)-x(O))*(y(Y)-y(O)))","(-(y(M)-y(O))*(x(X)-x(O))+(x(M)-x(O))*(y(X)-y(O)))/((x(Y)-x(O))*(y(X)-y(O))-(x(X)-x(O))*(y(Y)-y(O)))");

x2d=Point(1,0);o2d=Point(0,0);
t0=Angle(x2d,o2d,m2d);

// ainsi t0 est l'angle en 2D de XOM
// Attention il est entre 0 et 180, il faut cocher à la main
// le fait qu'il aille jusqu'à 360°.
// C'est pour cela qu'il n'est pas caché dans la ligne suivante

SetHide("_m2d,_x2d,_O2d,",true);

for (j=1; j<6; j++){
	gv=Point("M"+j,"x(O)+(-sqrt(Re*Re-Ri*Ri)*cos(_t0)*rsin(_j)-(Ri+Re*rcos(_j))*sin(_t0))*(x(X)-x(O))+(-sqrt(Re*Re-Ri*Ri)*sin(_t0)*rsin(_j)+(Ri+Re*rcos(_j))*cos(_t0))*(x(Y)-x(O))+Ri*rsin(_j)*(x(Z)-x(O))",
	"y(O)+(-sqrt(Re*Re-Ri*Ri)*cos(_t0)*rsin(_j)-(Ri+Re*rcos(_j))*sin(_t0))*(y(X)-y(O))+(-sqrt(Re*Re-Ri*Ri)*sin(_t0)*rsin(_j)+(Ri+Re*rcos(_j))*cos(_t0))*(y(Y)-y(O))+Ri*rsin(_j)*(y(Z)-y(O))");
	SetHide(gv,true);
}
qd1=Quadric("M1","M2","M3","M4","M5");

Ce script appelle plusieurs commentaires. Tout d’abord comme indiqué, on doit donner à l’angle la possibilité d’être rentrant (jusqu’à 360°) en cliquant sur l’icone associée comme ci-dessous :

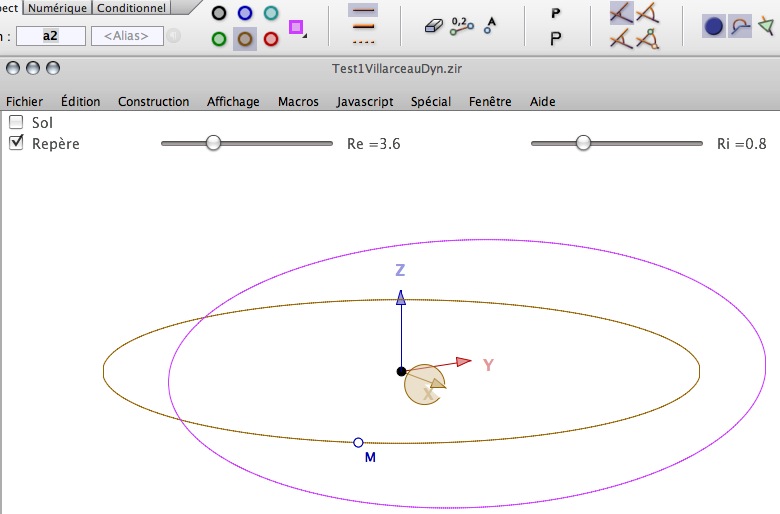
Ensuite on notera que t0 est un angle en degré, on a donc choisi de garder l’angle directement et de modifier le script en remplaçant les rcos(_t0) par des cos(t0).

Par ailleur on peut observer que l’angle t0 (généralement a2 dans la figure) est bien passé en contenu (et pas seulement en valeur numérique) comme on l’a souligné déjà en 1.c au début de cet article :

Voici la figure finale quand on applique sur cette figure le script précédent sur le tore par Villarceau

La figure finale est en manipulation directe dans l’onglet Manip1. Pour aller un peu plus loin dans ce domaine, dans un prochain article consacré à la récursivité, nous construirons des courbes récursives avec manipulation directe sur ses points de base.

Sur les cercles de Villarceau, il y a infiniment plus beau dans le film de Etienne Gyhs, Jos Leys et , Aurélien Alvarez en particulier sur cet extrait du film Dimension (choisir le chapitre 7) et l’article associé (largement illustré).

4. Galerie 3D en carscript

Simplement en guise de galerie 3D, quelques scripts autour de la cyclide de Dupin, considérée comme une inversion du tore (cyclides à anneau) : l’onglet précédent était l’occasion de montrer la technique de construction par des coniques sur le tore, nous allons juste l’appliquer en changeant de contexte.

Pour les construire, on utilise la paramétrisation donnée au lien précédent, avec les paramètres a, m et c avec c<= m <= a.

4.a Version statique 3D avec des polygones

Il s’agit simplement d’adpater la méthode de Alain Busser de construction par des polygones (voir les dernières pages de son poly en téléchargement en bas de cette page)

On évitera de dépasser n=26 (pour n=31 il faut 1 h de calcul). Sur des petites valeurs de n (16 à 20) on testera les valeurs différentes valeurs de c, m et a en particulier c=m et m=a. Le paramètre h désigne l’écart (en pourcentage du pas) entre deux polygones. On choisira h entre 0.9 et 0.97.

Pour la version colorée on prendra n pair. Mais on peut enlever la colorisation et conserver une version monochrome.

Exemple de productions du script

a) n= 24, m proche de c

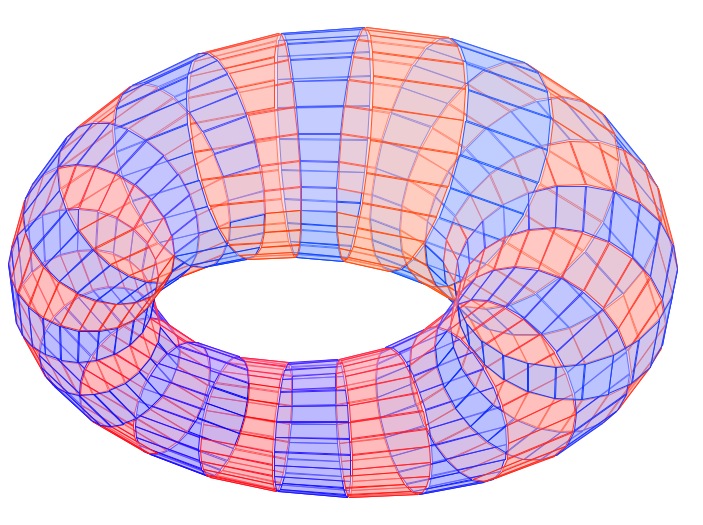
b) n= 20, m plus éloigné de c

c) n= 31 monochrome.

Le fichier est joint en téléchargement. Sur certaines machines, la figure peut mettre 25 min à s’ouvrir ... mais ensuite elle est manipulable. Trés joli ... Penser à prendre la bagette de switch pour voir avec tous les points.

p=Math.PI;n=24;h=0.97;
a=0.8;m=0.3;c=0.1;b2=Math.pow(a,2)-Math.pow(c,2);b=Math.sqrt(b2);
nbpair=0;
for (i=0; i<n; i++){
	ip=2*p*i/n;ihp=2*p*(i+h)/n;
	nbpair++;
	for (j=0; j<n; j++){
		jp=2*p*j/n;jhp=2*p*(j+h)/n;
		k=a-c*Math.cos(ip)*Math.cos(jp);
		kih=a-c*Math.cos(ihp)*Math.cos(jp);
		kjh=a-c*Math.cos(ip)*Math.cos(jhp);
		kh=a-c*Math.cos(ihp)*Math.cos(jhp);

		x=(m*(c-a*Math.cos(ip)*Math.cos(jp))+b2*Math.cos(ip))/k;
		y=b*Math.sin(ip)*(a-m*Math.cos(jp))/k;
		z=b*Math.sin(jp)*(c*Math.cos(ip)-m)/k;
		x=Math.round(10000*x)/10000;y=Math.round(10000*y)/10000;z=Math.round(10000*z)/10000;

		e=Point("x(O)+_x*(x(X)-x(O))+_y*(x(Y)-x(O))+_z*(x(Z)-x(O))",
		"y(O)+_x*(y(X)-y(O))+_y*(y(Y)-y(O))+_z*(y(Z)-y(O))");
		s=e;

		x=(m*(c-a*Math.cos(ihp)*Math.cos(jp))+b2*Math.cos(ihp))/kih;
		y=b*Math.sin(ihp)*(a-m*Math.cos(jp))/kih;
		z=b*Math.sin(jp)*(c*Math.cos(ihp)-m)/kih;
		x=Math.round(10000*x)/10000;y=Math.round(10000*y)/10000;z=Math.round(10000*z)/10000;


		e=Point("x(O)+_x*(x(X)-x(O))+_y*(x(Y)-x(O))+_z*(x(Z)-x(O))",
		"y(O)+_x*(y(X)-y(O))+_y*(y(Y)-y(O))+_z*(y(Z)-y(O))");
		s=s+","+e;

		x=(m*(c-a*Math.cos(ihp)*Math.cos(jhp))+b2*Math.cos(ihp))/kh;
		y=b*Math.sin(ihp)*(a-m*Math.cos(jhp))/kh;
		z=b*Math.sin(jhp)*(c*Math.cos(ihp)-m)/kh;
		x=Math.round(10000*x)/10000;y=Math.round(10000*y)/10000;z=Math.round(10000*z)/10000;

		e=Point("x(O)+_x*(x(X)-x(O))+_y*(x(Y)-x(O))+_z*(x(Z)-x(O))",
		"y(O)+_x*(y(X)-y(O))+_y*(y(Y)-y(O))+_z*(y(Z)-y(O))");
		s=s+","+e;

		x=(m*(c-a*Math.cos(ip)*Math.cos(jhp))+b*b*Math.cos(ip))/kjh;
		y=b*Math.sin(ip)*(a-m*Math.cos(jhp))/kjh;
		z=b*Math.sin(jhp)*(c*Math.cos(ip)-m)/kjh;
		x=Math.round(10000*x)/10000;y=Math.round(10000*y)/10000;z=Math.round(10000*z)/10000;


		e=Point("x(O)+_x*(x(X)-x(O))+_y*(x(Y)-x(O))+_z*(x(Z)-x(O))",
		"y(O)+_x*(y(X)-y(O))+_y*(y(Y)-y(O))+_z*(y(Z)-y(O))");
		s=s+","+e;
		SetHide(s,true);
		u=Polygon(s);
		if (nbpair==1){
			SetRGBColor(u,Math.round(90*j/n),Math.round(80*(1-Math.abs(2*i/n-1)))+Math.round(30*j/n),255);
		} else {
			SetRGBColor(u,255,Math.round(80*(1-Math.abs(2*i/n-1)))+Math.round(30*j/n),Math.round(90*j/n));nbpair=0;
		}
	}
}

4.b Version statique avec des coniques

Les fichiers sont bien moins lourds, on reprend la technique développée pour le tore. Voici 3 illustrations pour n=32 en trait fin

p=Math.PI;n=24;

a=0.5;m=0.25;c=0.2;b2=Math.pow(a,2)-Math.pow(c,2);b=Math.sqrt(b2);

for (i=0; i<n; i++){
	ip=2*p*i/n;
	for (j=1; j<6; j++){
		k=a-c*Math.cos(ip)*Math.cos(j);
		x=(m*(c-a*Math.cos(ip)*Math.cos(j))+b2*Math.cos(ip))/k;
		y=b*Math.sin(ip)*(a-m*Math.cos(j))/k;
		z=b*Math.sin(j)*(c*Math.cos(ip)-m)/k;
		x=Math.round(10000*x)/10000;y=Math.round(10000*y)/10000;z=Math.round(10000*z)/10000;
		e1=Point("A"+j+i,"x(O)+_x*(x(X)-x(O))+_y*(x(Y)-x(O))+_z*(x(Z)-x(O))",
		"y(O)+_x*(y(X)-y(O))+_y*(y(Y)-y(O))+_z*(y(Z)-y(O))");
		SetHide(e1,true);
	}
	q1=Quadric("A1"+i,"A2"+i,"A3"+i,"A4"+i,"A5"+i);SetRGBColor(q1,59,170,255);SetThickness(q1,"normal");
}

for (j=0; j<n; j++){
	jp=2*p*j/n;
	for (i=1; i<6; i++){

		k=a-c*Math.cos(i)*Math.cos(jp);
		x=(m*(c-a*Math.cos(i)*Math.cos(jp))+b2*Math.cos(i))/k;
		y=b*Math.sin(i)*(a-m*Math.cos(jp))/k;
		z=b*Math.sin(jp)*(c*Math.cos(i)-m)/k;
		x=Math.round(10000*x)/10000;y=Math.round(10000*y)/10000;z=Math.round(10000*z)/10000;
		e2=Point("B"+i+j,"x(O)+_x*(x(X)-x(O))+_y*(x(Y)-x(O))+_z*(x(Z)-x(O))",
		"y(O)+_x*(y(X)-y(O))+_y*(y(Y)-y(O))+_z*(y(Z)-y(O))");
		SetHide(e2,true);
	}
	q2=Quadric("B1"+j,"B2"+j,"B3"+j,"B4"+j,"B5"+j);SetRGBColor(q2,255,59,170);SetThickness(q2,"normal");

}

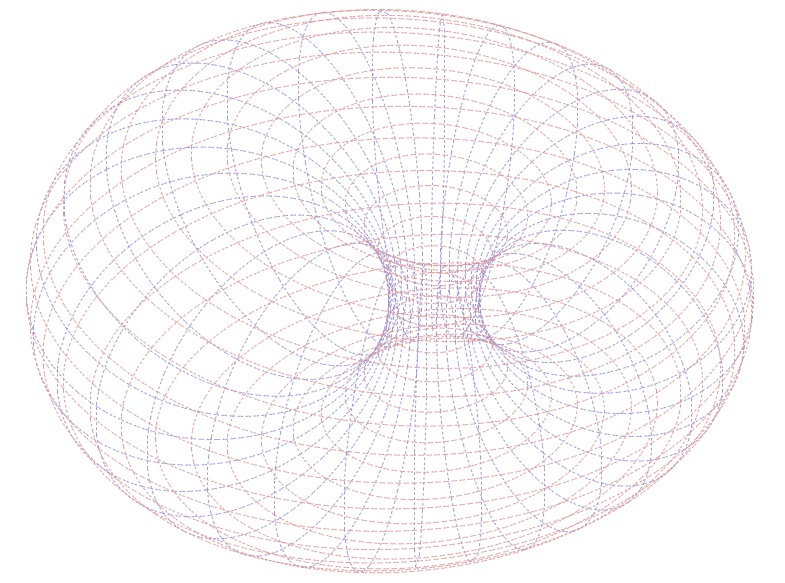
4.c Version dynaminque - avec des curseurs - par les coniques

On veut maintenant manipuler les coefficients a, m et c directement sur la figure. Pour cela on va prendre leurs valeurs par la longueurs de segments. On part alors d’une figure comme celle-ci (téléchargeable)

D’une manière générale, le rayon du grand cercle principal est (UB+UC)/2 et celui du petit (UB-UC)/2 (et donc la cycle est un tore si C est en U et avec un rayon central nul si C est en B. La distance entre les centres des cercles principaux est 2UA.

On obtient alors des productions de ce type (en manipulation directe dans un autre onglet)

p=Math.PI;n=23;

// Dans ce script je n'ai pas mis les round de Alain : il faut que n soit impair, premier est préférable.

// a=s1;
// m=s2;
// c=s3;

// b2=s1*s1-s3*s3;b=Math.sqrt(s1*s1-s3*s3)

// en pratique on a b=s4 et donc b2=s4*s4

for (i=0; i<n; i++){
	ip=2*p*i/n;cip=Math.cos(ip);sip=Math.sin(ip);
	for (j=1; j<6; j++){
		cj=Math.cos(j);sj=Math.sin(j);
		e1=Point("A"+j+i,"x(O)+(x(X)-x(O))*(s2*(s3-s1*_cip*_cj)+s4*s4*_cip)/(s1-s3*_cip*_cj)+s4*_sip*(s1-s2*_cj)/(s1-s3*_cip*_cj)*(x(Y)-x(O))+s4*_sj*(s3*_cip-s2)/(s1-s3*_cip*_cj)*(x(Z)-x(O))",
		"y(O)+(s2*(s3-s1*_cip*_cj)+s4*s4*_cip)/(s1-s3*_cip*_cj)*(y(X)-y(O))+s4*_sip*(s1-s2*_cj)/(s1-s3*_cip*_cj)*(y(Y)-y(O))+s4*_sj*(s3*_cip-s2)/(s1-s3*_cip*_cj)*(y(Z)-y(O))");
		SetHide(e1,true);
	}
	q1=Quadric("A1"+i,"A2"+i,"A3"+i,"A4"+i,"A5"+i);SetRGBColor(q1,59,170,255);SetThickness(q1,"thin");
}

for (j=0; j<n; j++){
	jp=2*p*j/n;cjp=Math.cos(jp);sjp=Math.sin(jp);
	for (i=1; i<6; i++){
		ci=Math.cos(i);si=Math.sin(i);
		e2=Point("B"+i+j,"x(O)+(x(X)-x(O))*(s2*(s3-s1*_ci*_cjp)+s4*s4*_ci)/(s1-s3*_ci*_cjp)+s4*_si*(s1-s2*_cjp)/(s1-s3*_ci*_cjp)*(x(Y)-x(O))+s4*_sjp*(s3*_ci-s2)/(s1-s3*_ci*_cjp)*(x(Z)-x(O))",
		"y(O)+(s2*(s3-s1*_ci*_cjp)+s4*s4*_ci)/(s1-s3*_ci*_cjp)*(y(X)-y(O))+s4*_si*(s1-s2*_cjp)/(s1-s3*_ci*_cjp)*(y(Y)-y(O))+s4*_sjp*(s3*_ci-s2)/(s1-s3*_ci*_cjp)*(y(Z)-y(O))");

		SetHide(e2,true);
	}
	q2=Quadric("B1"+j,"B2"+j,"B3"+j,"B4"+j,"B5"+j);SetRGBColor(q2,255,59,170);SetThickness(q2,"thin");

}

Voir les onglets suivants pour une manipulation directe de certaines figures

Tore par les cercles de Villarceau

<carmetal|doc=1881|largeur=790|hauteur=523>

Cyclique de Dupin par polygones - n=20

(figure de 776 Ko)

<carmetal|doc=1882|largeur=760|hauteur=570>

Cyclique de Dupin par coniques avec curseur - n=31

(figure de 524 Ko)

<carmetal|doc=1883|largeur=760|hauteur=570>