Exemple

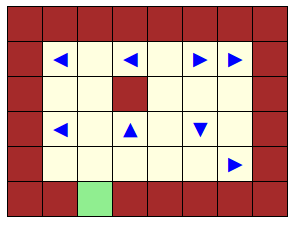
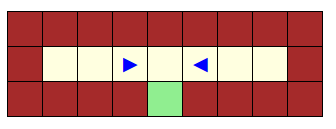
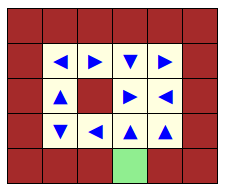
Le jeu ci-dessus ne permet qu’à un deux robots d’avancer :

avant	après A

En effet les autres robots ont devant eux un obstacle qui est soit un mur, soit un autre robot.

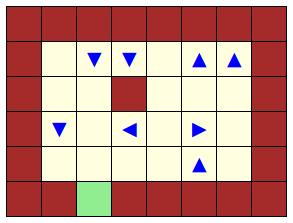
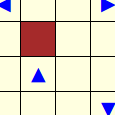
Alors que G produit l’effet

avant	après G

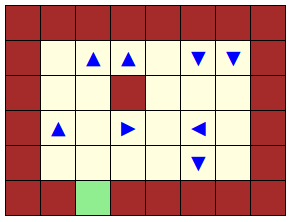
et D produit l’effet

avant	après D

En cliquant sur l’image ci-dessous, on peut jouer en ligne sur cet exemple (il suffit d’écrire un mot dans le cadre noir, à l’aide des lettres A, D et G) :

labyrinthes

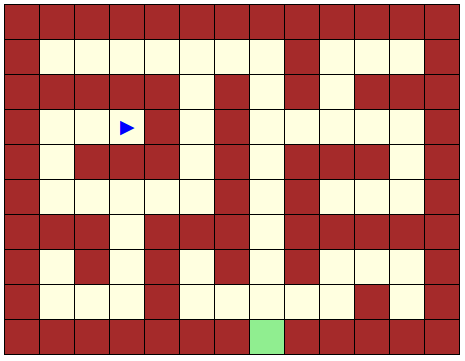
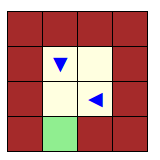
En fait robosomes est une généralisation des jeux de labyrinthe, comme on le voit sur cet exemple :

Interblocage

Ce jeu n’a pas de solution :

En effet dès qu’on réussit à faire approcher un des robots de la sortie, l’autre robot arrive en même temps et crée un embouteillage qui bloque la sortie.

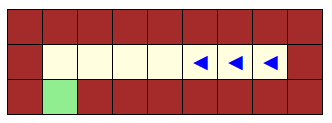
Le premier des jeux présentés ci-dessous n’a pas non plus de solution, ici l’embouteillage est provoqué par deux robots arrivant sur la même case mais de deux côtés différents :

Mais le second jeu (dessiné ci-dessus) possède une solution. Essayez (en ligne en cliquant sur l’image ci-dessus) !

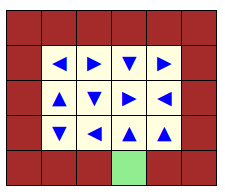
Une situation d’interblocage est connue, c’est celle où chaque robot est bloqué par un robot devant lui, comme ici :

Ce jeu possède pourtant une solution.

L’intérêt du jeu robosomes vient surtout du fait qu’il y a plusieurs robots qui peuvent se gêner les uns les autres, mais le blocage partiel de certains robots permet parfois de libérer le passage à d’autres robots [1]. En voici un exemple :

En jouant à ce jeu, on voit comment une file de robots avance : au début seul le premier bouge parce qu’il est le seul à ne pas avoir d’obstacle devant lui, mais ce faisant il libère la place devant le second qui bouge à son tour et ainsi de suite, la file s’allonge (jusqu’à presque doubler de longueur) en même temps qu’elle progresse :

Voici deux exemples où la grille est très encombrée mais où on peut faire sortir beaucoup de robots :

que des robots	une colonne centrale

Réussirez-vous à les faire sortir tous ?

Voici un robosomes inspiré par un jeu qu’Édouard Lucas décrivait sous le nom de prise de la Bastille :

Mise en œuvre

On peut dessiner une grille de robosomes à la craie, par terre, et placer sur les cases présentant des obstacles fixes, des chaises (qui ne bougeront pas au cours du jeu). La sortie [2] est signalée par un coloriage particulier ou un objet placé dessus (un mouchoir par exemple). Les robots sont interprétés par des élèves, que l’on place initialement selon le plan du jeu. Les robots ne doivent pas bouger sans qu’on le leur demande.

Un seul élève (ou une équipe peu nombreuse) donne les ordres à voix haute. Les robots exécutent les ordres simultanément :

• Si l’ordre est d’essayer d’avancer, les robots qui voient un obstacle (chaise ou autre robot) sur la case disposée devant eux, ne bougent pas. Les autres avancent d’une case.
• Si l’ordre est de tourner vers la gauche, les robots effectuent tous un quart de tour vers leur gauche. Ensuite on ajuste leur position au cas où certains d’entre eux auraient tourné d’un autre angle ou seraient sortis de leur case en tournant. Les élèves non latéralisés peuvent être munis de brassards de deux couleurs différentes avec charge de tourner vers leur brassard bleu (si c’est celui de gauche) .
• Si l’ordre est de tourner vers la droite, les robots doivent tous effectuer un quart de tour vers leur droite.

Si un robot arrive sur la case de sortie, il doit quitter le plateau. Comme pour les erreurs de rotation ou les conflits non résolus, il peut être nécessaire que l’enseignant.e joue le rôle d’arbitre.

Si un robot n’a pas respecté les règles du jeu, il est difficile de revenir en arrière (les autres robots ne se souvenant pas forcément de leur ancienne position, et il y aurait également risque d’erreur lors du retour en arrière). Dans ce cas il vaut mieux recommencer tout le jeu depuis la position initiale. Il en est de même si le programmeur a manifestement emprunté une voie sans issue.

Compétences travaillées

L’élève programmeur travaille la vision (dans l’espace) et la planification.

Les élèves robots travaillent le repérage dans l’espace, l’orientation (latéralisation) et la socialisation.

Théorie

En fait, chaque configuration du plateau peut être décrite par une matrice (dont chaque cellule porte un nombre décrivant si il y a un mur, une sortie ou un robot et dans ce cas, comment il est tourné) appelée état, et les états (de ce qui n’est jamais qu’un automate) sont divisés en trois catégories :

• l’état initial
• les états finaux (ceux où aucun robot ne subsiste sur le plateau)
• les états accessibles à partir de l’état initial.

Il en résulte que (en théorie) il est possible de trouver une solution à un robosomes [3] :

Éditeur

Le fichier suivant permet de fabriquer une matrice qu’il suffit de mettre dans l’un des jeux précédents pour créer son propre jeu de robosomes :