Excentricités
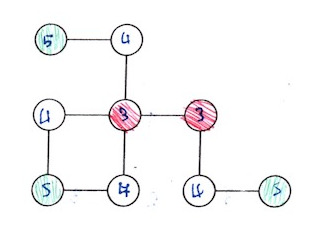
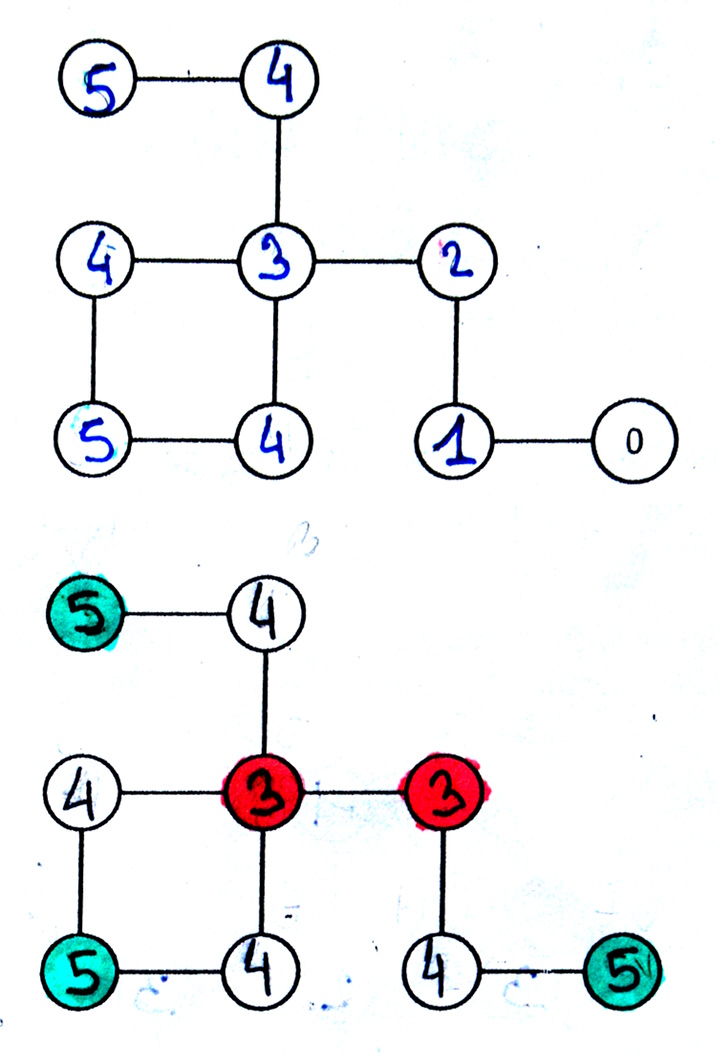
Bien que la notion d’excentricité ne soit pas explicitement au programme, elle est pratique parce qu’elle permet de trouver facilement les centres, rayon et diamètre. Pour cela, on peut calculer les distances d’un sommet (ici celui qui est en bas à droite) à tous les autres puis relever la distance maximale : c’est l’excentricité du sommet (ici 5, lu en haut à gauche)
Ensuite, bien que ce soit relativement long, l’excentricité de chaque sommet est calculée par cette méthode (ou « au feeling », beaucoup d’élèves y arrivent bien, une fois qu’ils ont compris ce qu’il faut faire) comme on le voit ci-dessus, ce qui permet de trouver
- les centres (coloriés en rouge)
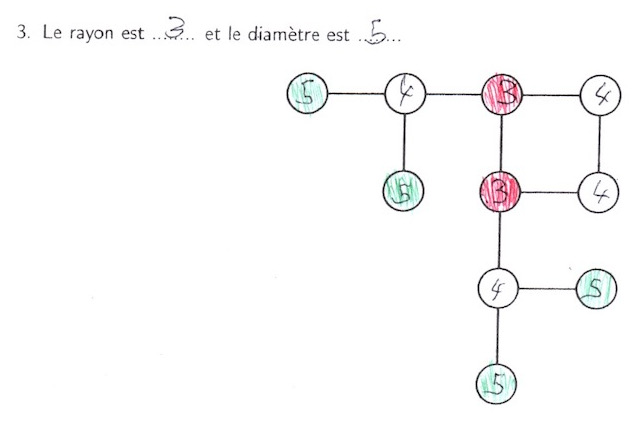
- le rayon (c’est la plus petite excentricité, ci-dessus 3)
- le diamètre (c’est la plus grande excentricité, ci-dessus 5)
En bonus on a le bord du graphe : ce sont les sommets coloriés en vert (comme les feuilles d’un arbre). Ni cette notion ni celle d’excentricité ne sont au programme mais les élèves n’ont pas éprouvé de difficulté particulière à identifier les sommets du bord (il y a eu moins d’erreurs que sur le centre).
Graphe 1
Le coloriage au crayon tend à être de meilleure qualité que celui au feutre :
Version crayon (à comparer avec l’onglet précédent) :

Version stylo-bille :
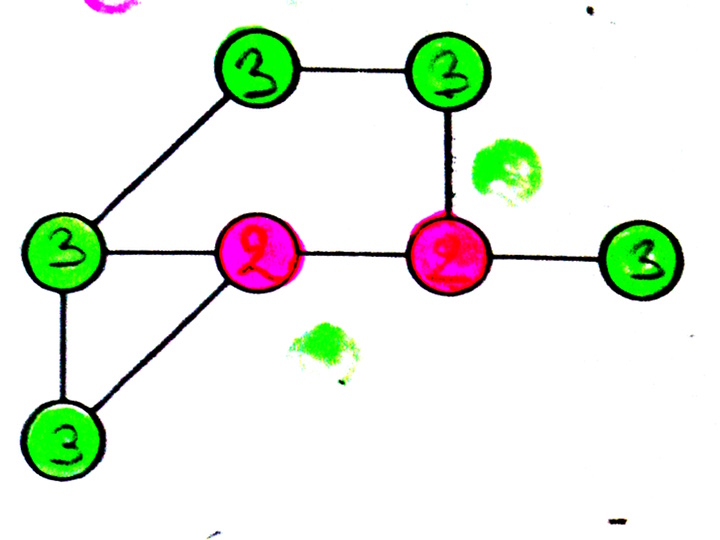
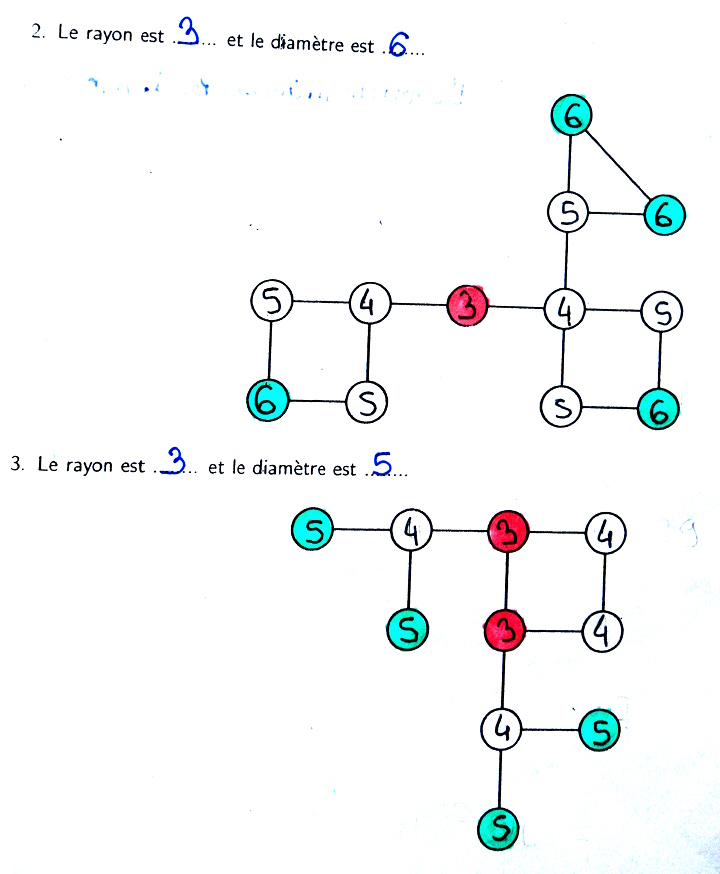
Graphe 2
Ce graphe présente une particularité : tous les sommets étant d’excentricité 2 ou 3, sont ou bien des centres, ou bien au bord.
Au crayon :

Au feutre (lequel traverse depuis la page suivante) :
Au stylo-bille :

Graphe 3
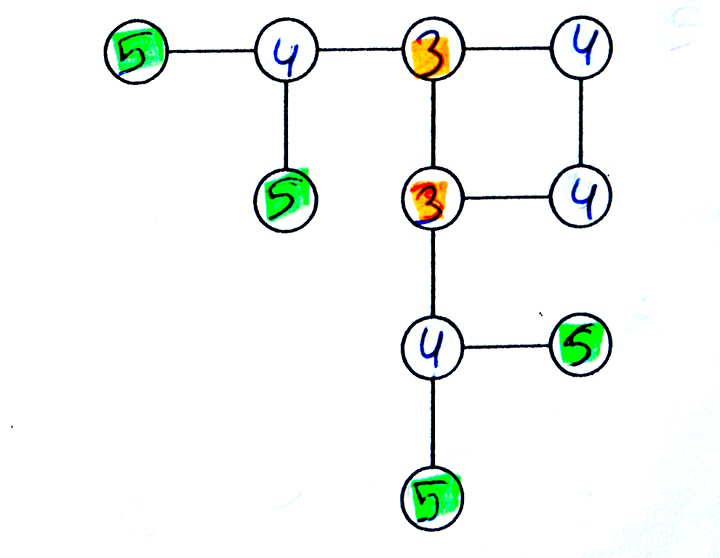
Ce graphe ne possède qu’un centre (ça arrive quand même parfois).
Au crayon :

Au feutre :

Au marqueur fluo :

Au stylo-bille :
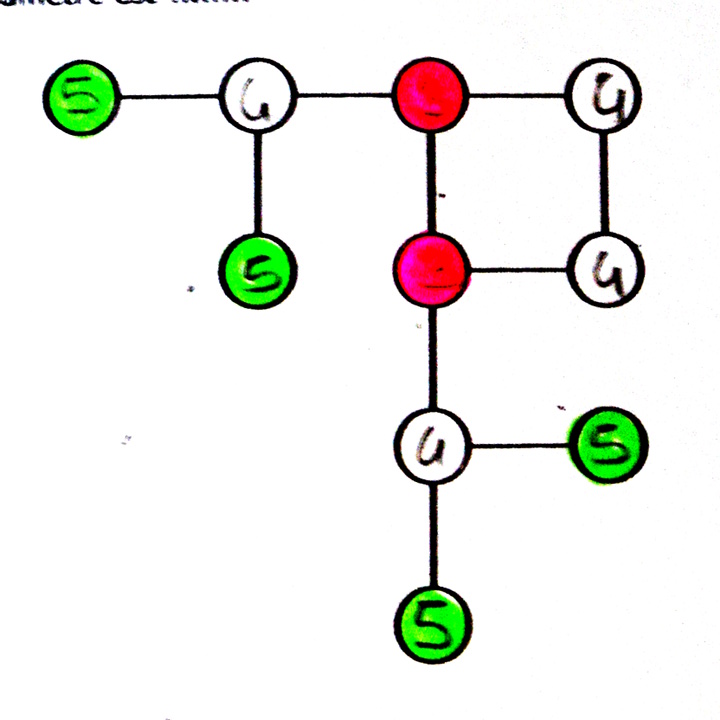
Graphe 5
Ce graphe ne possède lui aussi qu’un seul centre.
Au crayon :

Au feutre :

Au feutre également (avec une erreur de coloriage : un centre supplémentaire en bas, qui n’est en fait pas un centre) :
Confusion entre le calcul des distances à un sommet donné (choisi comme centre potentiel) et celui de toutes les excentricités :

Avec la question suivante, le graphe 5 ayant servi de support d’argumentation :
Mais avec une erreur (assez fréquente) dans l’interprétation : ce n’est pas le maximum du degré qui est souhaitable mais le minimum de l’excentricité.
Réseaux sociaux
La dernière question a parfois donné lieu à des erreurs. La plus répandue étant que l’information circule plus vite si le degré du sommet est important (alors que c’est son excentricité qui doit être minimale) comme à l’onglet précédent. Un autre exemple :

Court mais correct :

Rédaction un peu confuse mais l’idée y est :

Devoir un peu « littéraire » mais correct :

Question correctement traitée :

Explication par le dessin :
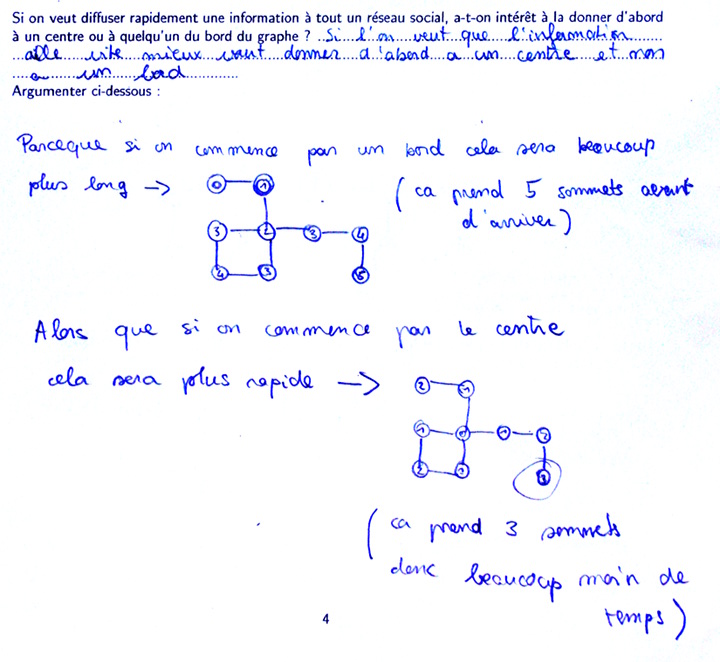
Idem mais dans le cas particulier d’un arbre :
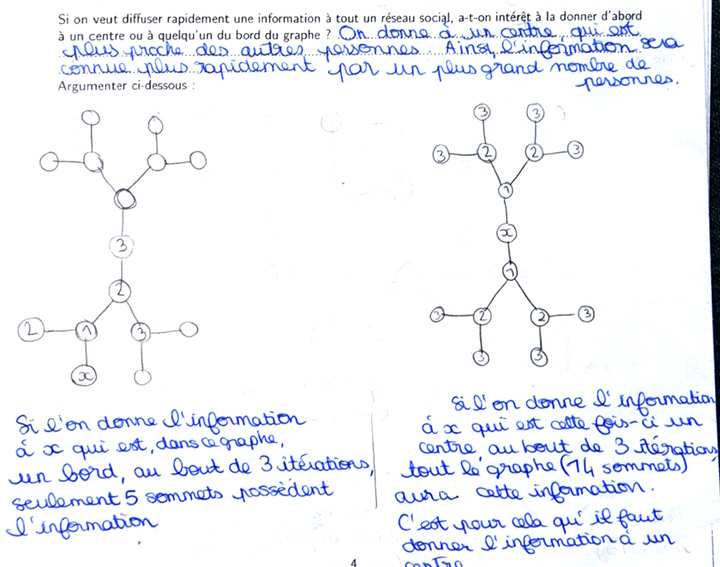
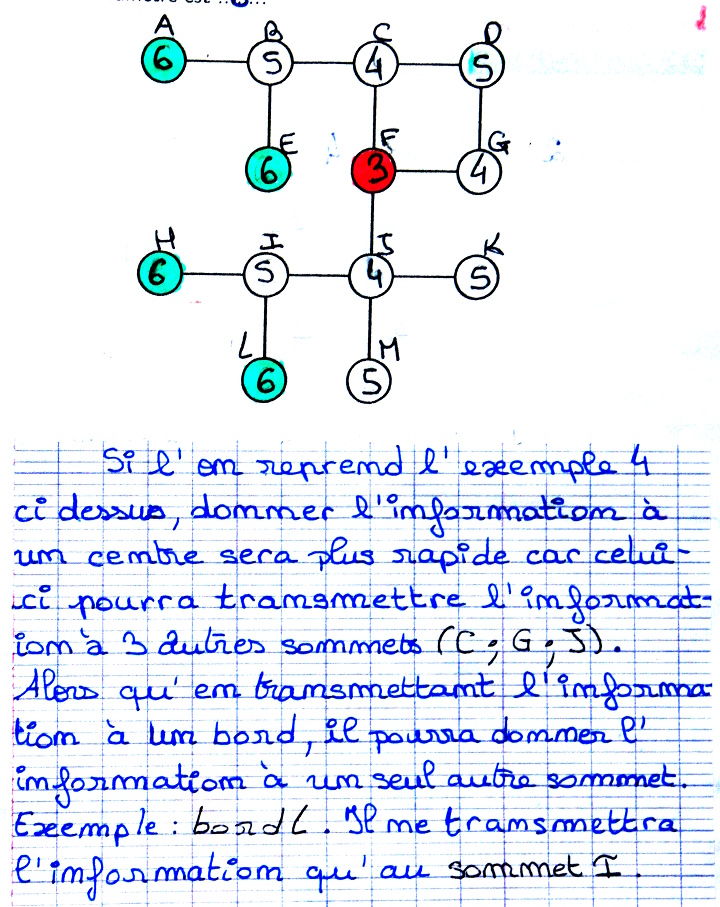
L’erreur la plus intéressante est la dernière : croire que si un sommet est relié à beaucoup de sommets, l’information circulera plus rapidement dans tout le graphe. En fait, c’est croire qu’une propriété locale (d’un seul sommet) déterminera la réponse à un problème global (tous les sommets). Ce genre de manipulation (en particulier le coloriage) permet de saisir les notions (centre, rayon, diamètre) mais cela ne marche qu’une fois que les élèves ont commencé l’exercice, or beaucoup veulent « d’abord comprendre » et sont bloqués devant l’exercice.
DocEval
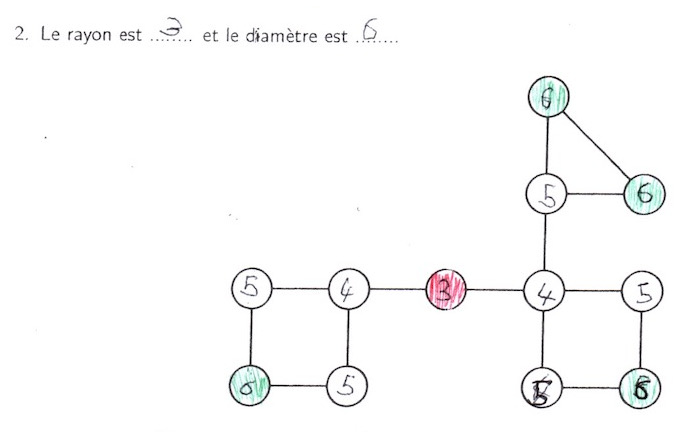
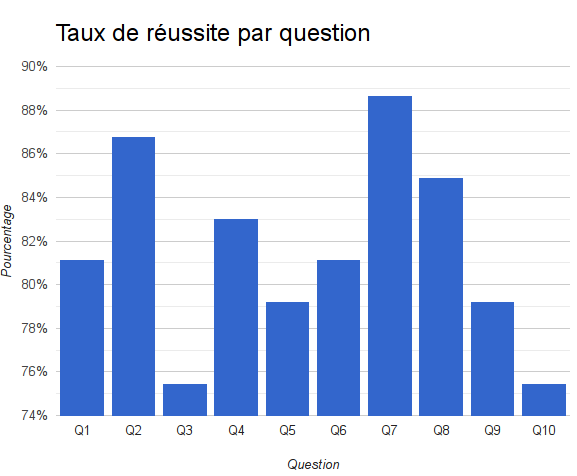
Après ce devoir, deux classes de 2nde ont été évaluées en ligne sur DocEval. Il y avait 10 questions :
- 3 questions « quel est le rayon de ce graphe ? »
- 3 questions « quel est le diamètre de ce graphe ? »
- 3 questions « combien de centres ? »
- 1 question sur l’article 222-33-2-2 du code pénal, lui aussi au programme.
C’est cette dernière question qui a été la moins réussie :
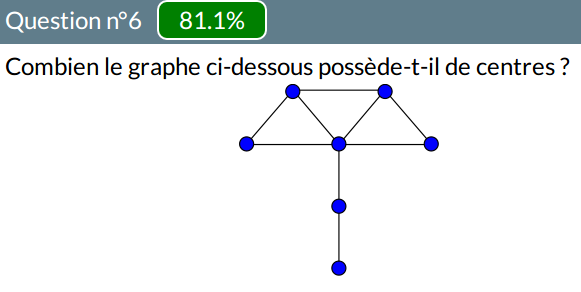
Centres
Le dénombrement de centres de ce graphe a été aussi peu réussi que la question sur le code pénal :

Il y a quand même deux élèves qui ont cru que tous les sommets sont des centres :
Les centres de ce graphe sont en bas :

Plusieurs élèves n’ont vu que celui tout en bas (surprenant) ou seulement les deux qui le surmontent (plus logique, vu la symétrie du graphe) :
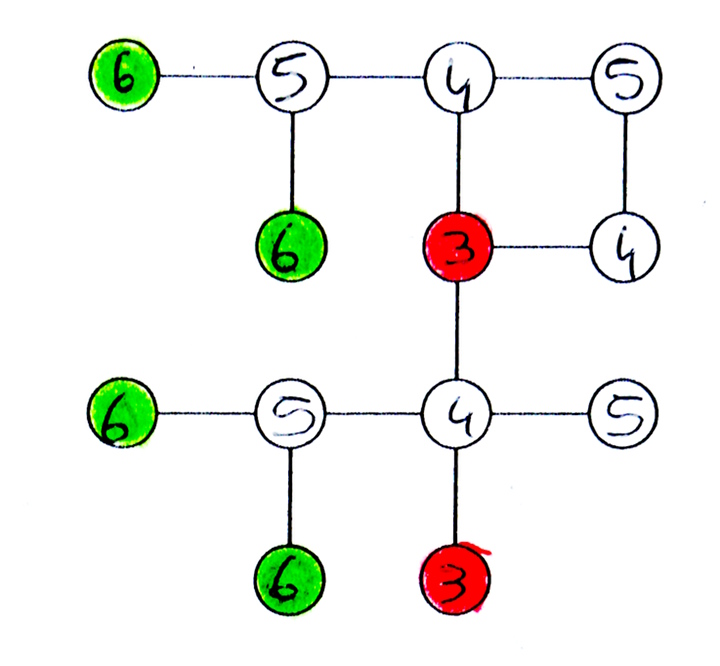
Ce graphe également est symétrique :
Les erreurs semblent venir d’une estimation de l’altitude des sommets (3 sommets vers le milieu) :
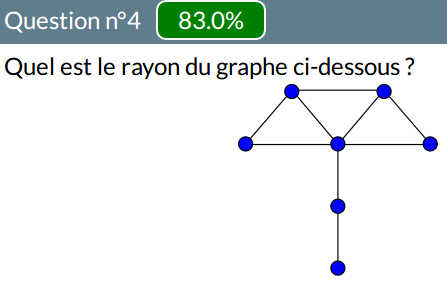
Diamètre
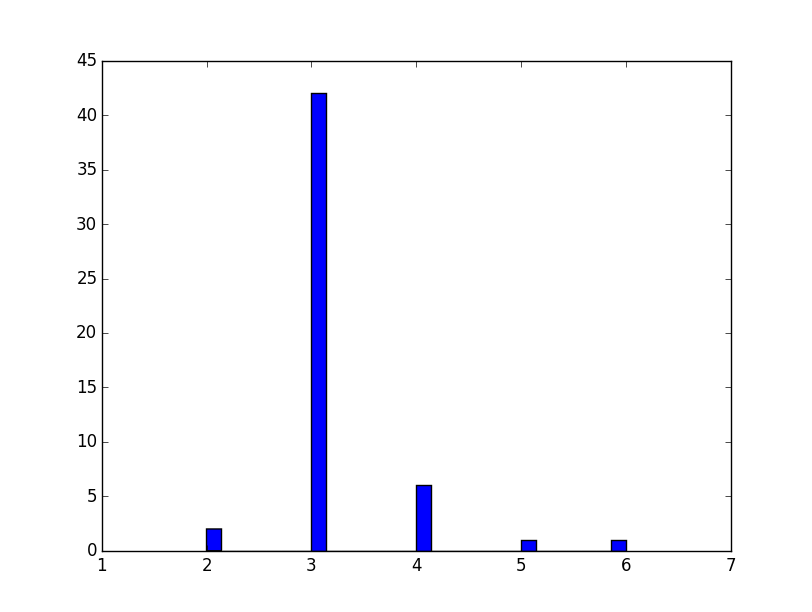
Il y a eu pas mal d’erreurs sur le diamètre de ce graphe :
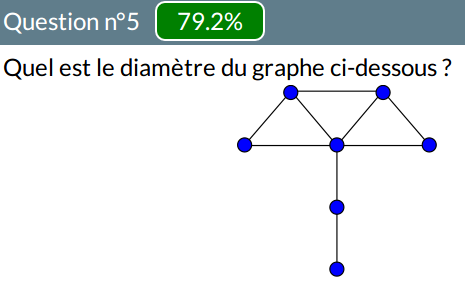
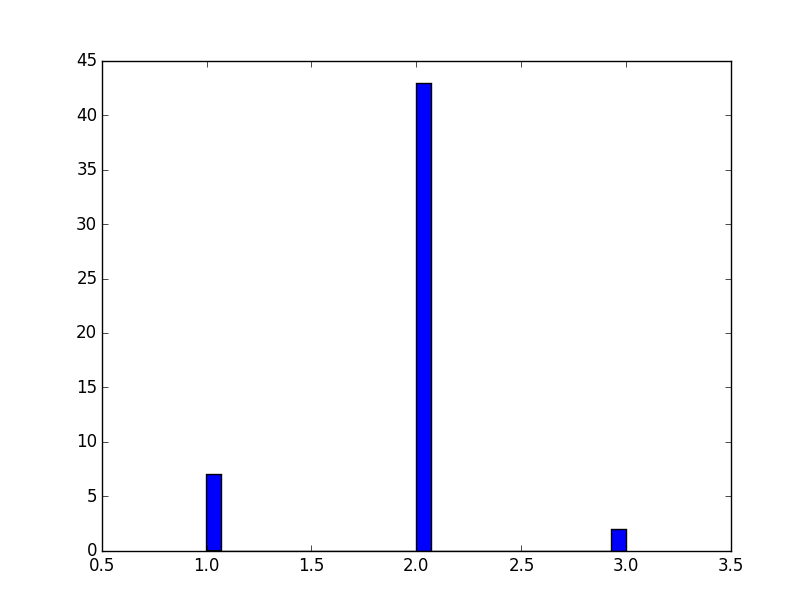
La distribution des diamètres est asymétrique avec une certaine tendance à la surestimation :
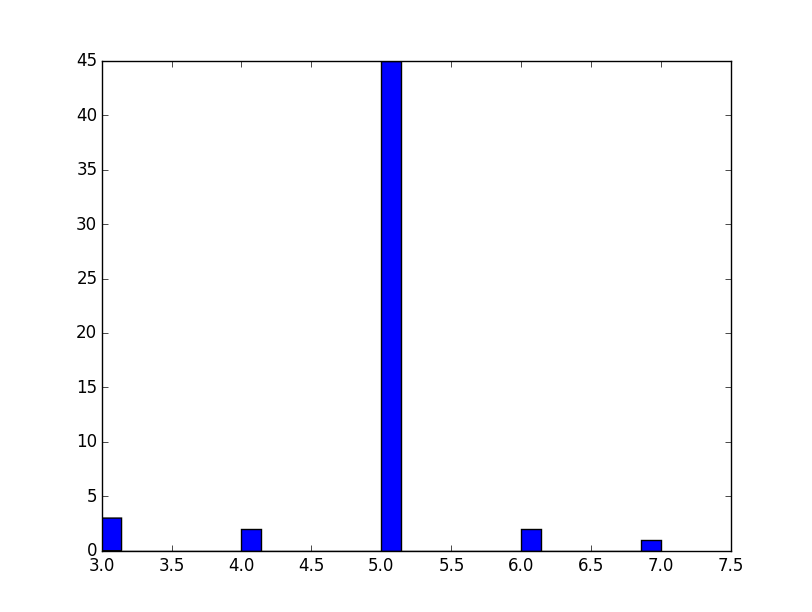
Pour ce graphe :

la distribution des diamètres est plus symétrique :
Et pour celui-ci :
la distribution montre également une nette tendance à la surestimation :
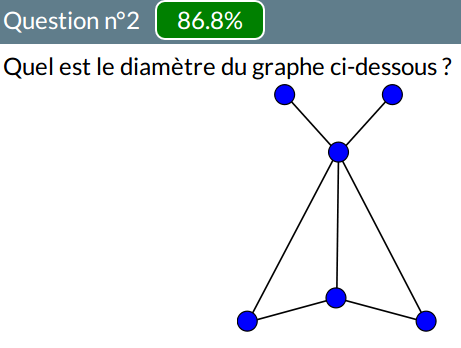
Rayon
Pour ce graphe :
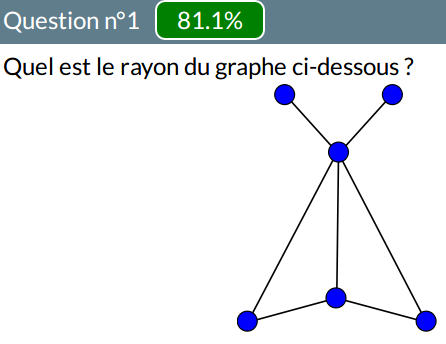
le rayon a parfois été largement surestimé :
Il est possible que la réponse 5 soit une mauvaise lecture de l’énoncé : peut-être qu’au lieu d’estimer le rayon, l’élève a voulu compter les rayons ? En tout cas l’un des élèves ayant répondu 5, a également trouvé 5 centres. Au passage une élève a trouvé un rayon de 3 et un diamètre de 2 !
Pour ce graphe
on constate une tendance à la sous-estimation :
L’élève ayant donné un rayon de 7, avait trouvé un diamètre de 5, et a reconnu avoir mieux compris à la fin de l’évaluation (qu’il a fallu l’obliger à faire car élève en situation de déscolarisation semble-t-il).
Et pour ce graphe
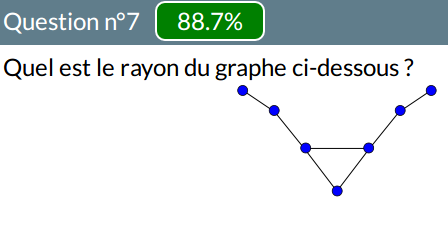
on trouve aussi un rayon largement surestimé :
Là encore, les erreurs sur les rayons sont corrélées avec celles sur le diamètre et sur le nombre de centres.
Le sujet a semblé abstrait pour beaucoup d’élèves (mais facile pour beaucoup d’élèves aussi, pas les mêmes). Une possibilité serait de faire une activité débranchée similaire à celle-ci, où chaque sommet serait occupé par un élève et un message serait donné à un des élèves, avec mission de le transmettre à ses voisins, puis la même mission serait confiée aux voisins (donner le message à chaque voisin etc) et les élèves qui ne sont pas sur le graphe compteraient le nombre d’étapes, avec in fine discussion sur l’identité de l’élève à qui remettre le message en premier (identification des centres du graphe). Pour être plus réaliste, on peut explorer aussi la variante où chaque élève ne peut diffuser l’information qu’à un seul de ses voisins à la fois. Dans le cas des arbres, cette variante (hors programme) est décrite dans l’onglet diffusion de cet article. L’expérience sera tentée lorsque les conditions sanitaires le permettront.








Commentaires