Programmation de la Numworks sans Numworks
Pourquoi donc ?
Le programme de Seconde recommande l’usage du clavier pour programmer (« programmation textuelle »). Le clavier des calculatrices étant nettement moins pratique que celui des ordinateurs, programmer en Python sur une calcularice est un véritable exploit pour qui a des doigts un peu gros, ou souffre de presbytie (quand ce n’est pas les deux). Pour remédier à ces problèmes, les calculatrices sont dotées de menus déroulants où on peut choisir des instructions ou blocs d’instructions tout faits [1], mais également de la possibilité de communiquer avec l’ordinateur, l’idée étant de programmer la calculatrice depuis l’ordinateur. À ma connaissance, la Numworks est la première calculatrice permettant de communiquer avec n’importe quel ordinateur (pas nécessairement du type Microsoft ou Mac) par le biais du logiciel Chrome, disponible sur toutes plateformes. Cela permet de programmer ses modules Python sur tout ordinateur, puis de les transférer vers la Numworks afin de les y utiliser. En respectant toutefois une limite de place : L’ensemble des modules Python ne doit pas occuper plus de 4096 octets. Ceci dit on peut aussi transférer et utiliser des modules Python créés par d’autres personnes (collègues, chercheurs, élèves). En voici quelques exemples.
Comment donc ?
S’il n’est pas nécessaire d’acheter une Numworks© ni un Windows© avec Edge©, deux prérequis sont nécessaires. Mais ils sont gratuits :
- le logiciel Chrome, à télécharger sans frais puis installer ;
- créer un compte sur le site Numworks. Le mien est ici
Une fois mon compte créé, pour programmer un module Python sur la Numworks, je n’ai plus qu’à cliquer sur « nouveau script » en bas de ma page d’accueil, et je me trouve alors sur une page comprenant un éditeur Python en ligne, à gauche, et un simulateur de Numworks à droite. En haut de ladite page, j’ai la possibilité de nommer mon script (ici, comme il s’agit des diviseurs d’un entier, j’ai choisi de l’appeler divisors.py ) et après avoir, pour une première fois, cliqué sur « sauvegarder », chaque fois que je relance ce simulateur (en cliquant sur « relancer ») il importe automatiquement le module en cours d’édition :

Ceci fait que chacune des fonctions que j’aurai créée dans le module pourra être utilisée dans la console (directement en mode interactif, dans la calculatrice). Par exemple, si on entre dans cette console, « gcd(12,16) », on a un message d’erreur parce que Python ne possède pas par défaut de fonction gcd (calculant le pgcd de deux entiers). Mais une fois le module divisors.py importé, comme celui-ci comprend une telle fonction, « gcd(12,16) » affiche 4.
Cette philosophie est très proche des recommandations de l’inspection générale : Il est pénible de créer une boucle dans la console, alors si on veut faire des choses compliquées, on les fait dans des définitions de fonctions (à l’intérieur du module) et on réserve les utilisations de fonctions (affichages par exemple) à la console.
repl
L’acronyme REPL signifie
- Read (attendre une entrée par l’utilisateur)
- Eval (évaluer ce qui a été entré, et qui est supposé être une expression)
- Print (afficher sur la console le résultat de l’évaluation)
- Loop (et recommencer le cycle R-E-P en boucle)
C’est ainsi que fonctionnent les consoles Python des calculatrices ou autres. Souvent on appelle cela « utiliser Python comme calculatrice » et l’utilité du repl pour apprendre un langage de programmation par essais et erreurs, est telle qu’un site internet y est consacré : repl.it lequel a évidemment sa version Python. Là encore, il est mieux d’avoir un compte, mais on peut programmer en ligne, avec un Python à la fois léger et puissant, sans problèmes d’installation donc.
Intersection de listes
Pour la suite on aura besoin de calculer l’intersection de deux listes l1 et l2. Une manière rapide est d’utiliser une compréhension de liste : La liste intersection est formée des éléments x de l1 qui sont aussi dans l2. En Python cela s’écrit :
def inter(l1,l2):
return [x for x in l1 if x in l2]intersection d’intervalles
Avec cette fonction, on peut explorer les objets range de Python, en calculant les intersections de tels objets :

Cela permet de vérifier expérimentalement la commutativité de l’intersection, mais aussi le sens de range et accessoirement, de constater que l’intersection de deux intervalles est toujours un intervalle, éventuellement vide.
Diviseurs et divisibilité
diviseurs
Pour calculer la liste des diviseurs d’un entier n, on part de 2 constatations :
- La définition : « on dit que a est un diviseur de b (ou que b est un multiple de a) s’il n’y a aucun reste lorsqu’on divise euclidiennement a par b. Comme le reste euclidien de a par b se note a%b, en Python, le fait que a est divisible par b se note
a%b==0; - Un diviseur de n ne peut pas être plus grand que n, donc les diviseurs potentiels de n ne sont à chercher que parmi les entiers entre 1 et n compris.
La liste des diviseurs de n peut donc se décrire en compréhension comme formée des entiers d entre 1et n tels que la division de n par ces entiers ne laisse aucun reste :
def divisors(n):
return [d for d in range(1,n+1) if n%d==0]En guise d’application, le script suivant (exécuté sur la Numworks, réelle ou virtuelle) permet de vérifier que le millésime 2017 était premier mais qu’il faudra attendre un peu avant d’avoir de nouveau une année « première ». Le script
for n in range(2017,2025): print(divisors(n))
produit l’effet suivant :

Arithmétique
Primalité
En affichant la liste des diviseurs de plusieurs entiers (voir ci-dessus de 2017 à 2024), on constate qu’aucun entier n’a moins que deux diviseurs (1 et l’entier lui-même) mais que certains entiers atteignent ce minimum. Les premiers d’entre eux étant 2, 3, 5, 7, 11, 13, 17 et 19. Cette propriété remarquable (avoir peu de diviseurs) justifie une définition : Un tel entier est appelé premier. Comme, en Python, le nombre de diviseurs est appelé longueur de la liste (abrégé len comme length), on propose alors ce test de primalité :
def isPrime(n):
return len(divisors(n))==2Remarque : Ce test de primalité (traduction directe de la définition en Python) n’est pas le meilleur, en terme d’efficacité, qui soit. On qualifie en général de naïf un tel algorithme. La recherche de tests de primalité efficaces est un domaine assez pointu des mathématiques, toujours en développement. On pense notamment à Derrick Lehmer...
On peut alors s’intéresse au nombre pi(n) de nombres premiers inférieurs à n (répartition des nombres premiers), avec ce préambule
from kandinsky import *et ces rajouts au script
def pi(n):
return [isPrime(k) for k in range(2,n+1)].count(True)
def courbe():
for x in range(2,320):
set_pixel(x,200-pi(x),color(0,0,255))Il faut ...un certain temps, à la Numworks, pour dessiner la répartition :
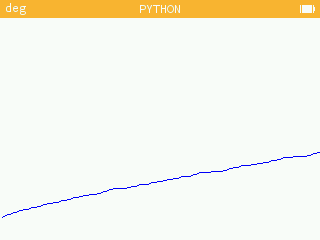
Perfection et amitié
Python possédant une fonction sum, il est très facile de définir la fonction « somme des diviseurs » en appelant sum(divisors(n)). L’affichage de telles sommes permet de constater (avant preuve) que
- la somme des diviseurs de n est au minimum n+1 (minimum obtenu pour n premier)
- par conséquent la somme est toujours supérieure à n.
- Mais elle peut être
- inférieure à 2n (nombre déficient)
- égale à 2n (nombre parfait)
- supérieure à 2n (nombre abondant).
D’où le test de perfection suivant :
def isPerfect(n):
return sum(divisors(n))==2*nSi on incorpore le test dans le script divisors.py, on peut chercher les nombres parfaits inférieurs à 1000 en entrant successivement
l = [n for n in range(2,1000) if isPerfect(n)]
print(l)Ce qui affiche que seuls trois nombres inférieurs à 1000 sont parfaits :

Autre définition : On dit que a et b sont amicaux si sum(divisors(a))=a+b et sum(divisors(b))=a+b aussi. Cette notion aussi peut être explorée expérimentalement avec le script divisors.py
pgcd
Puisqu’on dispose maintenant de la liste des diviseurs et de l’intersection, on peut assez naturellement envisager de parler de diviseurs communs à deux entiers :
def cd(a,b):
return inter(divisors(a),divisors(b))Cela permet de parler de plusieurs notions :
- nombres premiers entre eux
- probabilité que deux nombres soient premiers entre eux
- pgcd

Il arrive assez souvent que deux entiers n’aient qu’un diviseur commun (le nombre 1). En ce cas on les dit premiers entre eux. Ce qui suggère une nouvelle fonction pee (comme « premiers entre eux ») :
def pee(a,b):
return len(cd(a,b))==1Avec le préambule
from kandinsky import *
from random import *et l’affichage
def premiers():
s,t = 0,0
for x in range(320):
t += 1
if pee(randint(2,1001),randint(2,1001)):
s += 1
set_pixel(x,200-int(200*s/t),color(255,0,0))le code premiers() produit ce genre d’affichage, montrant une stabilisation vers la « probabilité que deux nombres soient premiers entre eux » :
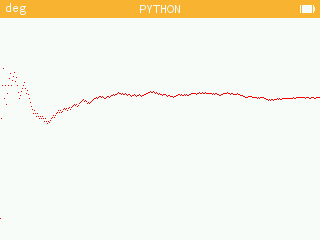
Au fait quelle est cette probabilité ?
Enfin, afficher de grands nombres d’exemples d’appels à la fonction cd montre que les diviseurs communs à a et b sont les diviseurs d’un nombre qui est le plus grand de la liste cd(a,b). Le plus grand (« greatest ») des diviseurs communs peut donc être défini par cette fonction :
def gcd(a,b):
return max(cd(a,b))Là encore il s’agit d’une simple traduction en Python de la définition « le pgcd de a et b est le plus grand des diviseurs communs à a et b » et peut donc être qualifié d’algorithme « naïf » de calcul du pgcd. L’algorithme d’Euclide est nettement plus efficace par exemple.
Conclusion
L’idée de programmer des fonctions Python dans un (ou plusieurs) module vu comme une collection d’algorithmes, et de n’aller dans la console (en mode repl) que pour utiliser ces fonctions (affichage de valeurs) rend la Numworks très conforme à l’esprit du programme de mathématiques du lycée. De plus, la limite de 4096 octets au total incite à produire du code court et concis, avec des fonctions imbriquées, ce qui permet de se concentrer sur l’algorithme et non les détails n’en faisant pas partie comme les subtilités de matplotlib et autres tkinter. Et l’occasion est belle de découvrir les listes en compréhension, chères aux mathématiciens [2]. On ne peut alors qu’espérer que Casio, au hasard, permette également une programmation Python de sa calculatrice, qui soit accessible à tout le monde et pas seulement aux victimes de Gafam...
Annexes
La version R
On remarque que R est par défaut en mode « repl » (pas besoin de print pour afficher la valeur d’une expression) et qu’il n’est pas nécessaire d’y définir l’intersection de listes, puisque celle-ci existe déjà :
library(ggplot2)
divisors<-function(n){
l<-seq(1:n)
return(l[ n%%l ==0 ])
}
isPrime<-function(n){
return( length(divisors(n)) == 2)
}
pi<-function(n){
l<-seq(1:n)
return(sum(sapply(l,isPrime)))
}
courbePi<-function(n){
x<-seq(1:n)
y<-sapply(x,pi)
df<-data.frame(x,y)
graphe<-ggplot(df, aes(x,y))
graphe+geom_point(aes(colour=y))+scale_color_gradient(low="green", high="red")
}
isPerfect<-function(n){
return( sum(divisors(n)) == 2*n)
}
parfaitInf<-function(n){
l<-seq(1:n)
return(Filter(isPerfect,l))
}
cd<-function(n,p){
return( intersect( divisors(n),divisors(p) ) )
}
gcd<-function(a,b){
return(max(cd(a,b)))
}
#Tests
divisors(15)
isPrime(15)
pi(15)
courbePi(1000)
isPerfect(3)
parfaitInf(100)
intersect(seq(1:10),c(2,5))
cd(20,15)
gcd(20,15)Le script ci-dessus peut être exécuté sans installation de R, par exemple en le copiant-collant sur ce site. Ce qui produit, pour la partie sur la représentation graphique de la fonction de compte des nombres premiers, ceci :
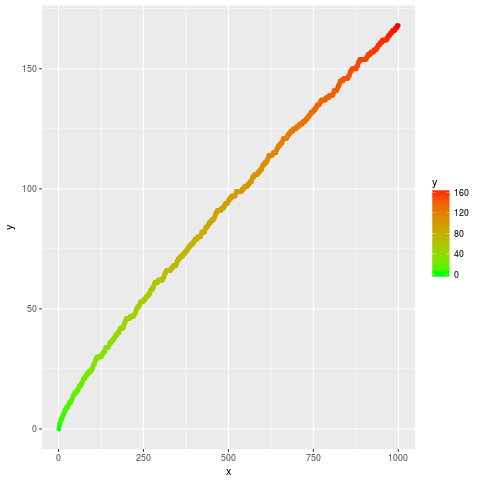
La version haskell
Le langage haskell est célèbre pour ses compréhensions, et donc parfaitement adapté à la présente activité. Voici le source :
import Data.List
diviseurs n = [d | d <- [1..n], n <span class="base64" title="PGNvZGUgY2xhc3M9InNwaXBfY29kZSBzcGlwX2NvZGVfaW5saW5lIiBkaXI9Imx0ciI+bW9kPC9jb2RlPg=="></span> d == 0]
isPrime n = length (diviseurs n) == 2
isPerfect n = sum (diviseurs n) == 2*n
cd a b = (diviseurs a) <span class="base64" title="PGNvZGUgY2xhc3M9InNwaXBfY29kZSBzcGlwX2NvZGVfaW5saW5lIiBkaXI9Imx0ciI+aW50ZXJzZWN0PC9jb2RlPg=="></span> (diviseurs b)
pgcd a b = maximum (cd a b)
cm a b = [m | m <- [1..], m <span class="base64" title="PGNvZGUgY2xhc3M9InNwaXBfY29kZSBzcGlwX2NvZGVfaW5saW5lIiBkaXI9Imx0ciI+bW9kPC9jb2RlPg=="></span> a == 0, m <span class="base64" title="PGNvZGUgY2xhc3M9InNwaXBfY29kZSBzcGlwX2NvZGVfaW5saW5lIiBkaXI9Imx0ciI+bW9kPC9jb2RlPg=="></span> b == 0]
ppcm a b = head (cm a b)Et quelques exemples d’utilisation :
> [n | n <- [1..100], isPrime n]
[2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97]> pgcd 24 36
12> [n | n <- [6..1000], isPerfect n]
[6,28,496]Le module divisors.py
Voici l’intégralité du code du module :
def inter(l1,l2):
return [x for x in l1 if x in l2]
def divisors(n):
return [d for d in range(1,n+1) if n%d==0]
def isPrime(n):
return len(divisors(n))==2
def cd(a,b):
return inter(divisors(a),divisors(b))
def gcd(a,b):
return max(cd(a,b))On peut s’en servir dans toute distribution Python, pas nécessairement celle de la Numworks.
Le vrai algorithme du vrai Euclide
Malgré le lien entre Euclide et la division euclidienne, le premier n’utilisait pas la seconde pour calculer un pgcd, mais des soustractions, avec cet algorithme :
def pgcd(a,b):
while a!=b:
a,b = max(a,b)-min(a,b),min(a,b)
return aL’activité présentée ici est maintenant disponible parmi les activités Numworks :
Les deux documents sont téléchargeables au format pdf sur le site Numworks, dans les pages ci-dessus.



Commentaires