Dans les figures suivantes, les traits marron représentent des bâtons de bois, dont la longueur est donc fixe (mais ils peuvent tourner !). Le noir représente des objets métalliques (rivets pour les articulations ou règles le long desquelles quelque chose glisse). Le bleu représente ce que l’on manipule (poignée ou fil tendu), et le rouge est le stylo, ou la trace qu’il laisse sur la feuille.

Ellipsographe de Delaunay

La petite baguette ayant une longueur fixe, le point bleu décrit un cercle. Les points noirs sont fixes sur les baguettes qui les soutiennent. Alors le losange réalise une affinité, qui transforme le cercle en... une ellipse. Télécharger la figure (en cliquant sur le dessin) puis l’ouvrir avec CaRMetal pour arrêter ou relancer l’animation.

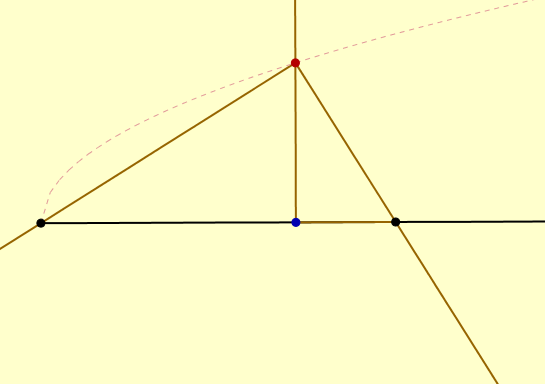
Traceur de parabole de Cavalieri

Une équerre est verticale (côté horizontal coulissant, et angle droit en bleu), et une autre équerre passe par les points noirs et a son angle droit sur la branche verticale. Alors l’angle droit trace une parabole, ou plutôt une demi-parabole : il faudrait une deuxième machine symétrique par rapport à celle-ci, pour avoir une parabole complète. Manipuler le point bleu avec la souris (clic gauche) pour voir la machine en action.

Hyperbolographe à fil tendu

Un fil bleu est tendu entre chaque point bleu (manipulable à la souris) et un point noir (fixe). Le fil est tendu contre une baguette articulée autour de l’autre point noir, par un stylo rouge qui l’appuie contre la baguette. Alors les mouvements des stylos sont sur des arcs d’hyperbole. Manipuler l’un des points bleus avec la souris (clic gauche) pour voir la machine en action.

Antiparallélogrammes

Dans les figures ci-dessous, une « mauvaise » manipulation mène à un parallélogramme (qui ne construit rien). D’où le nom d’antiparallélogrammes donné aux figures « utiles ». On peut construire une hyperbole ou une ellipse avec ces antiparallélogrammes.

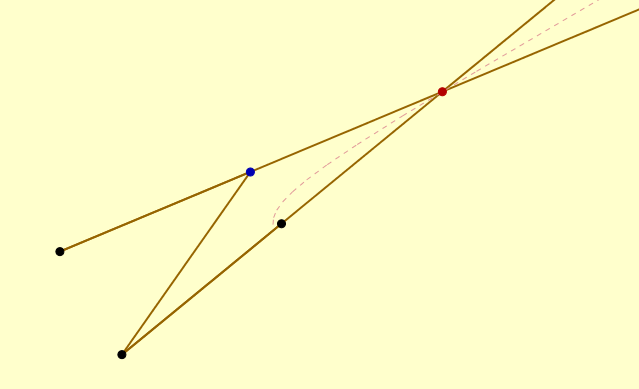
Traceur d’hyperbole. C’est à l’intersection des deux baguettes les plus longues qu’on place le stylo rouge. Et c’est toujours le point bleu qu’on manipule. En fait cet appareil ne construit que le quart d’une hyperbole... Manipuler le point bleu avec la souris (clic gauche) pour voir la machine en action.

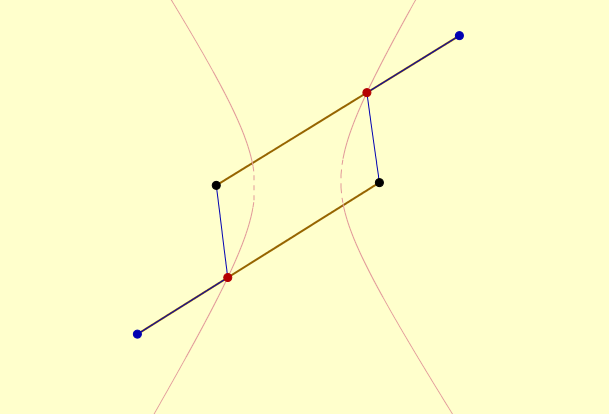
Traceur d’ellipse. Les deux segments issus du point bleu ont une longueur constante (donc le point bleu parcourt un cercle), ainsi que le segment joignant les deux foyers de l’ellipse. D’ailleurs pendant la moitié de l’animation, on voit le parallélogramme... Les deux baguettes les plus longues se croisent là où on place le stylo. On constate alors que seule la moitié supérieure de l’ellipse est tracée (quand on a un vrai parallélogramme, le stylo rouge est à l’infini...). Cliquer sur la figure pour la télécharger et l’ouvrir avec CaRMetal.