Premier TP : Représentation graphique
Pour représenter graphiquement une fonction, on l’approxime en général par un polygone ayant un grand nombre de points et dont les côtés sont donc petits et nombreux. Ce qu’il est impossible de faire sans une boucle parcourant les abscisses successives des points de la courbe.
Ceci dit, si on renonce à joindre les points, tout en les maintenant nombreux, on a un nuage de points qui évoque assez bien la représentation de la fonction.
L’idée vient, une fois de plus, du livre de Guillaume Connan.
Ceci dit, lorsqu’on dessine un nuage de points, l’algorithmique n’est plus nécessaire, on peut aussi dessiner un seul point, activer sa trace, puis utiliser le Monkey...
Le sujet du TP est téléchargeable ici, d’un clic droit :
En Seconde, même en début d’année, ce TP est une réussite, si on tient compte de l’enthousiasme des élèves (« c’est génial, cet algorithme ! »). Par contre il a été impossible de l’évaluer, les questions notées de la deuxième page ayant été presque complètement ratées.
Certains élèves, victimes de leur zèle, ont constaté qu’en lâchant le Monkey au bout d’un temps trop long, celui-ci reste actif, ce qui a au moins l’avantage de déclencher l’hilarité...
La question II/2 a été très difficile aux yeux des élèves, ce qui en Seconde, est nouveau : Pour la plupart des élèves, les techniques algébriques de résolution d’inéquations sont inédites ou mal conceptualisées.
La question III a toujours été mal faite, les élèves ayant trouvé l’algorithme si « génial » qu’ils ont cru le voir partout (y compris sur un tableur, où pourtant on n’utilise pas de nombres aléatoires). Avec 2000 points, l’algorithme donne ceci :
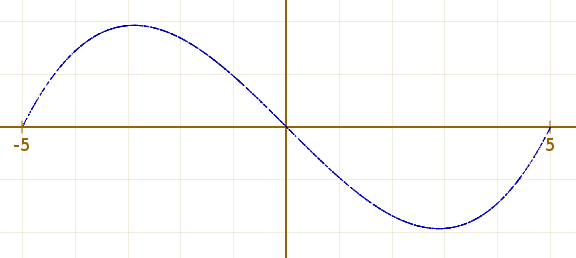
alors qu’avec 101 points (pas de 0,1) l’approximation polygonale donne ceci :
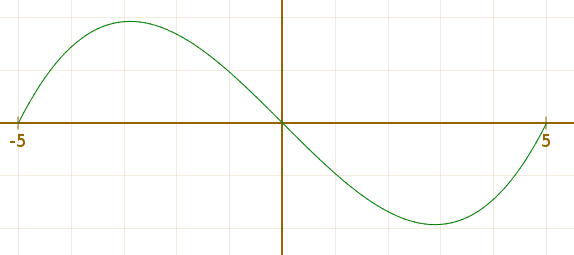
Par contre, la représentation par points aléatoires est utilisée pour les surfaces implicites par le logiciel 3D-XplorMath
Deuxième TP : Recherche d’extrema
La méthode du thermomètre a déjà été utilisée pour optimiser une fonction de deux variables. Elle peut aussi servir à chercher le maximum d’une fonction non monotone sur un intervalle. Là encore, le point est déplacé aléatoirement pour éviter de provoquer des réflexions métaphysiques sur ce qui se passe dans la boucle. Et là encore, JavaScript n’est pas nécessaire et on peut là encore, utiliser le Monkey.
Voici le sujet :
Il est intéressant de voir comment des élèves pour qui la notion de boucle est encore en cours d’acquisition, se trompent lorsqu’ils essayent de taper au clavier au lieu de cliquer sur une boucle toute faite comme CaRMetal le permet. L’erreur la plus répandue est celle consistant à écrire
for(i=0; i=200; i+=1)On sent là un besoin de décrire la boucle comme un intervalle (de i=0 jusqu’à i=200) et non comme JavaScript le fait, par une initialisation suivie d’un test pour rester dans la boucle (on reste dans la boucle tant que i reste inférieur ou égal à 200). Dans cette optique, il est intéressant de voir l’historique du logiciel Xcas, dont le langage de programmation ressemble à JavaScript, mais auquel il y a quelque temps, a été ajouté une version française « pour i de 0 jusque 200 faire ».
De façon générale, la première cause de blocage reste la lecture trop superficielle du sujet. Ainsi beaucoup d’élèves ne regardent même pas les deux premières lignes, et le texte
le point M ailleurs que sur les axes et la courbe
a souvent été compris comme son contraire
le point M sur les axes ou la courbe
Ce qui éclaire sur certaines difficultés rencontrées en probabilités...
Seuls deux élèves ont fini le TP avant la fin de l’heure, et encore ils n’ont pas fait le II/3. Le TP est donc trop long, et il eût peut-être été mieux de ne pas faire le I qui a été long. Cependant, la réponse obtenue au I/8 est plus précise que celle du II, ce que certains élèves ont d’ailleurs remarqué spontanément.
Pour aller plus loin, (pour les élèves qui iraient vraiment plus vite que les autres), on peut penser à faire chercher les valeurs exactes des extrema et leurs antécédents, en demandant de calculer une valeur approchée de $\frac{5\sqrt{3}}{3}$, puis la valeur exacte et la valeur approchée de l’image de ce nombre.
Nombres triangulaires
Pour calculer les nombres triangulaires (sujet à la mode) par une boucle, il est visiblement souhaitable d’utiliser le mode pas-à-pas, pour que les élèves aient le temps de voir ce qui se passe, à leur rythme. Comme CaRMetal n’a pas de mode pas-à-pas, et bien qu’on puisse simuler celui-ci, le premier TP sur les boucles a été fait sous Open Office Calc, ce tableur étant doté du langage JavaScript via l’interpréteur rhino, le même que CaRMetal.
La syntaxe des boucles en JavaScript semble complexe, mais elle est très conforme au vocabulaire de la Terminale L : Une phase d’initialisation, typiquement i=0, puis une condition, non de sortie, mais pour rester dans la boucle, et enfin le corps de la boucle, où l’indice i est incrémenté.
Voici le sujet d’un TP sur les nombres triangulaires en mode pas-à-pas :
Additionner une colonne de nombres avec un tableur n’est visiblement pas une compétence largement acquise à l’entrée en Seconde (le bouton $\Sigma$ n’est pas connu des élèves), ni bien entendu le « dollar ». Les élèves semblent par contre autant à l’aise avec le tableur de GeoGebra qu’avec celui d’Open Office.
Somme toute (c’est le cas de le dire !), la question la plus intéressante de ce TP a été la question non notée.
Tableur : Un seul élève a vu que la colonne contenant les doubles des nombres triangulaires était formée par des produits de valeurs de l’indice.
Pour entrer les nombres triangulaires dans la colonne B du tableur, les élèves, qui ignorent totalement le symbole « dollar » et son utilisation, ont entré les nombres à la main (recopiés de la feuille de TP). Pourtant l’algorithme suggérait d’entrer la formule
=B1+A2dans la cellule B2, et de copier cette formule vers le bas. Il semble que l’usage du tableur en collège ne va pas jusqu’à là...
GeoGebra
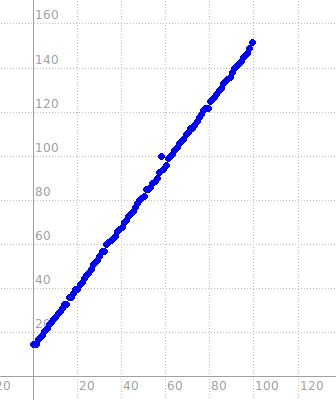
Les élèves ont découvert, émerveillés, que GeoGebra a aussi un tableur, mais là aussi, ils ont entré les nombres à la main. L’étape suivante a été de sélectionner les colonnes A et B du tableur, puis choisir (après clic droit) de « créer un nuage de points ». Puis après un zoom pour voir tous ces points, la seule instruction qui leur a été donnée a été « c’est une régression qu’il faut faire ; cherchez parmi les outils de régression de GeoGebra ». Cette instruction a suffi à guider les élèves vers la régression polynomiale, spontanément ! Voici la version avec curseur (objet que les élèves ne connaissent pas) :
<geogebra|doc=4540|largeur=691|hauteur=542>
En manipulant le curseur, on trouve pour quelles valeurs du degré la courbe passe par les points ; les élèves ont changé le degré par essais et ont trouvé la formule.
Xcas
Certains élèves avaient Xcas sur leur ordinateur, d’autres pas. Ceux-là sont allés sur Xcas en ligne et y ont tapé l’instruction. Aucun n’a pensé à factoriser l’expression affichée...
La dernière question tombe un peu comme un cheveu sur la soupe : Son but est de montrer que pour additionner les entiers consécutifs, il y a un autre algorithme que celui avec la boucle ci-dessus. Par exemple, il semble a priori plus facile de calculer $\frac{10 \times 11}{2}$ que de calculer 1+2+3+4+5+6+7+8+9+10.
Un problème se pose : Les élèves doivent pour comparer les deux algorithmes, admettre que ces deux nombres sont égaux pour toute valeur de n, la démonstration par récurrence n’étant pas franchement au programme de Seconde ! Il reste l’explication offerte par le fameux dessin du rectangle coupé en deux :
<geogebra|doc=4541|largeur=689|hauteur=512>
En attendant, les élèves ont eu à faire confiance à Xcas, ce qui évidemment ne leur a posé aucun problème.
Fonctions affines
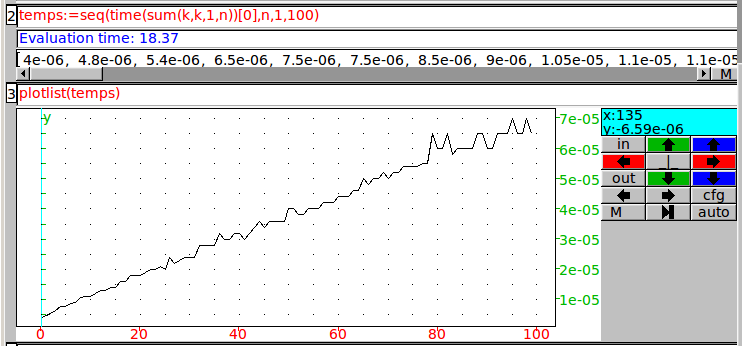
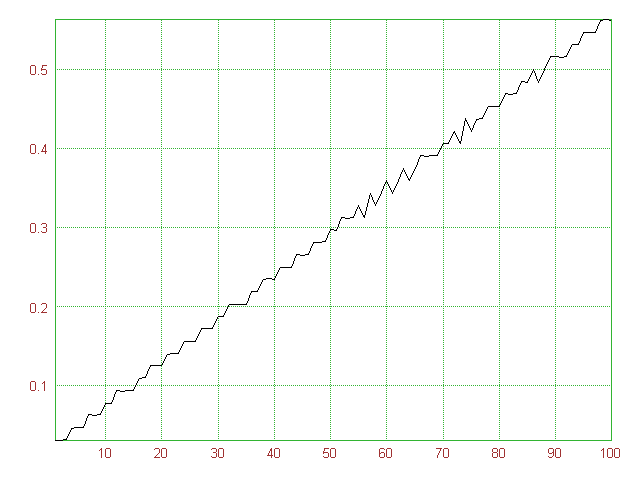
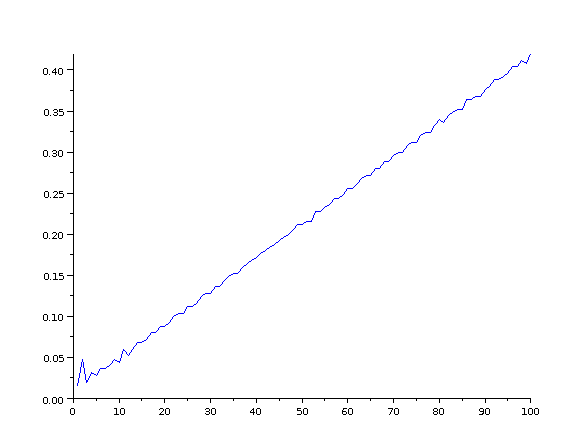
Pour voir s’il est plus rapide de calculer la somme terme à terme ou d’effectuer le produit de n par n+1 et diviser par 2, on a besoin d’outils permettant de mesurer le temps.
Ainsi, à partir de mesures de temps d’exécution de programmes, on peut aborder par une problématique (estimer le temps de calcul de nombres triangulaires) les fonctions affines. Pour ne pas multiplier à l’excès les TP d’algorithmique, un devoir maison a été donné aux élèves, dont voici l’énoncé :
Avec une moyenne de 13,86, ce devoir est plutôt réussi. Le fait de travailler sur des fonctions affines « issues du monde réel » a plutôt motivé les élèves, qui voient apparemment mieux ce qui se passe parce que les fonctions affines sont moins abstraites que celles du cours. On peut donc parler d’enseignement basé sur une problématique dans ce cas. Par contre, il s’agit bel et bien d’une régression linéaire et non d’une vraie fonction affine, ce qui rend l’exercice un peu prématuré en Seconde.
Cette activité est intéressante en Seconde parce que
- Elle est expérimentale ; qu’on aime ou qu’on n’aime pas, l’expérimentation est au programme de Seconde ;
- Elle utilise des boucles imbriquées ;
- Elle utilise de la statistique (lissage par moyenne mobile, recherche de minimum, calcul de moyenne) ;
- Elle utilise l’algorithmique comme objet d’étude pour un problème de maths (d’habitude, c’est plutôt le contraire) ;
- Elle introduit les fonctions affines dans un enseignement basé sur la problématique, comme le demande le programme de Seconde ;
- Elle permet même, avec les unités en jeu, de faire un peu de révision sur les écritures scientifiques...
Pour voir d’autres exemples de mesure de temps de calcul, on peut essayer avec l’algorithme d’Euclide ou le calcul de nombres de Fibonacci.





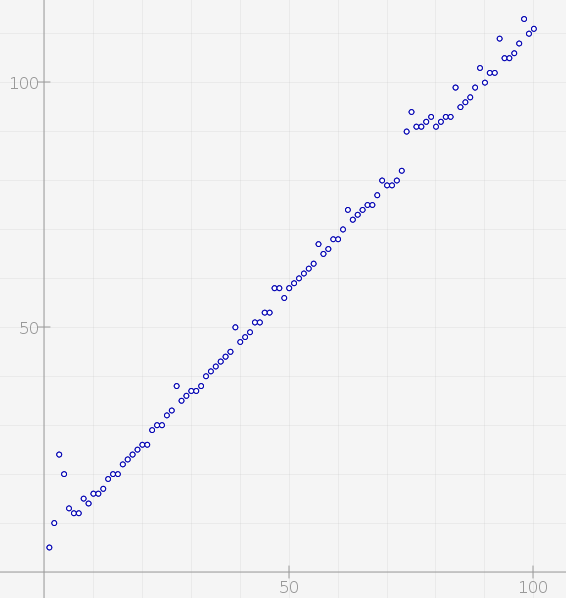
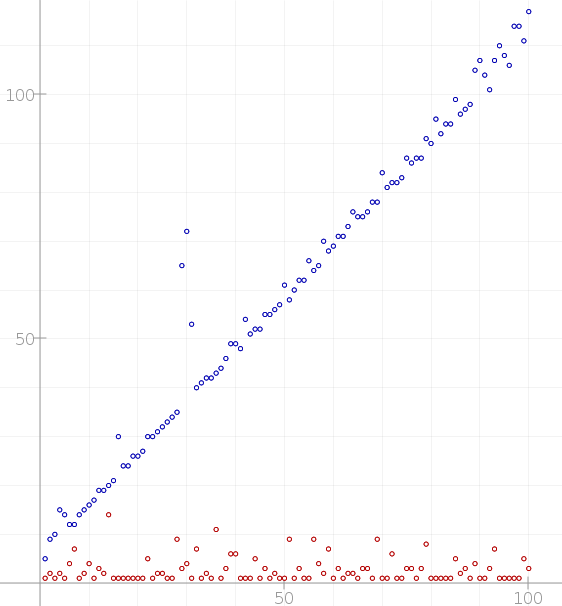




Commentaires