Pour dessiner ce graphe, il faut cocher chaque case de la matrice d’adjacence correspondant à une arête du graphe. Pour cela, on utilise la correspondance suivante entre les noms des sommets :
| dans le sujet | dans l’application |
| A | A1 |
| B | A2 |
| C | A3 |
| D | A4 |
| E | A5 |
Les cases à cocher sont alors les suivantes :
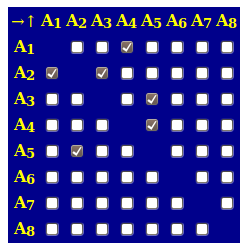
Ce qui dessine le graphe :

Si l’application réagit un peu lentement, c’est parce qu’à chaque mise à jour du graphe, les puissances de la matrice d’adjacence sont calculées, jusqu’à la puissance septième, laquelle permet (par ses coefficients nuls) de voir les sommets non joignables entre eux ; l’absence de coefficient nul de cette matrice permet de conclure que le graphe est connexe. Ici ce n’est pas le cas à cause des sommets A6, A7 et A8, isolés du reste ; mais on voit sur la puissance septième que le bloc correspondant aux sommets A1 à A5 n’a aucun coefficient nul, ce qui montre que le graphe formé par les 5 premiers sommets est connexe :

En utilisant le fichier html comme mémoire de stockage des matrices, la concision de CoffeeScript permet d’implémenter une multiplication de matrices 8 fois 8 en trois lignes :
for ligne in [1..8]
for colonne in [1..8]
somme = 0
somme += (Number $("#B1l#{ligne}c#{k}").text())*(Number $("#B#{puissance-1}l#{k}c#{colonne}").text()) for k in [1..8]
$("#B#{puissance}l#{ligne}c#{colonne}").text sommeEn fait, Number convertit du texte (le coefficient de la matrice, à la lecture dans le document) en nombre ; et quand le coefficient du produit est calculé, il est reconverti en texte avec text. Ce qui évite d’avoir à rajouter des instructions spécifiques pour l’affichage.
Le fichier est ici, mais également ci-dessous, manipulable en ligne.
Graphe à 8 sommets
Programmation du graphe
Chaque sommet est considéré comme relié à lui-même:


Commentaires