Pendant que les élèves placent les points dans le repère (la fonction à représenter était $x \mapsto x^2$, avec pour unités 1 cm sur l’axe des $x$ et 1 mm sur l’axe des $y$), le prof (c’est moi !) écrit au TBI (sous CaRMetal) le script suivant :

a=Point(-6,3.6);
SetShowValue(a,true);
for(x=-6;x<=6;x=x+0.1){
	y=x*x/10;
	Move(a,x,y);
	Pause(400);
}

dont l’effet est de produire un film, dont l’unique acteur qui est un point, effectue un parcours sur la représentation graphique. La question posée aux élèves était « pourquoi l’ordonnée initiale du point a est-elle 3,6 alors que le carré de -6 n’est pas 3,6 ? ». Ce point semble avoir été plutôt une aide pour la construction sur papier millimétré, les élèves semblant être plus familiers des repères orthonormés que des repères non orthonormés.

Par la suite, pendant que le nuage de points apparaissait sur les feuilles de papier millimétré, le script ci-dessus a été modifié par celui ci-dessous qui est plus statique :

a=Point(-6,3.6);
SetHide(a,true);
for(x=-6;x<=6;x=x+0.1){
	y=x*x/10;
	b=Point(x,y);
	Pause(200);
}

qu’il est d’ailleurs assez facile de transformer en quelque chose que les élèves reconnaissent (« ah oui, ça ressemble au papier millimétré ») :

a=Point(-6,3.6);
SetHide(a,true);
for(x=-6;x<=6;x=x+0.5){
	y=x*x/10;
	b=Point(x,y);
	SetPointType(b,"cross");
	Pause(200);
}

(dans les deux cas, les deux premières lignes, réminiscences du premier script, sont totalement inutiles. Elles sont là uniquement pour préparer la suite).

Pour avoir une « courbe », il a suffi de joindre les points a et b par un segment, ce que produit la modification suivante du script :

a=Point(-6,3.6);
SetHide(a,true);
for(x=-6;x<=6;x=x+0.1){
	y=x*x/10;
	b=Point(x,y);
	SetHide(b,true);
	s=Segment(a,b);
	Pause(200);
}

Las ! La figure obtenue est celle-ci :

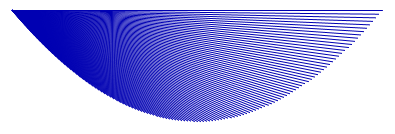
• • « Il y a un bogue ».
    • « Oui mais c’est joli ».
  • « C’est quand même bogué, où est l’erreur ? ».
    • « C’est pas grave Monsieur, c’est plus joli que la courbe sur le papier ».

Le bogue [1] vient de ce tous les points b sont reliés au même point a. Il suffit donc de réaffecter a par b pour avoir les segments voulus :

a=Point(-6,3.6);
SetHide(a,true);
for(x=-6;x<=6;x=x+0.1){
	y=x*x/10;
	b=Point(x,y);
	SetHide(b,true);
	s=Segment(a,b);
	a=b;
	Pause(200);
}

Voilà une excellente manière de montrer une affectation de variable dans un contexte non numérique !

L’activité m’a permis de constater que les élèves ont spontanément trouvé la corrélation entre la qualité du graphique et le nombre de points à tracer (j’avais dit « une vingtaine de points au minimum », et ils ont été d’accord, contrairement à leurs prédécesseurs) mais aussi qu’un seul élève sur 30 a eu envie d’utiliser la règle pour joindre les points : Il semble évident aux élèves de Seconde modernes qu’une courbe n’est pas un polygone, tout autant que le fait que lorsque les points sont nombreux et rapprochés, le polygone ressemble quand même beaucoup à la courbe.

Il va de soi qu’il y a des moyens plus simples pour représenter graphiquement une fonction. En CarScript par exemple :

c=CartesianFunction(-6,6,"x^2/10");

Ceci dit, comme le dit le programme :

Même si les logiciels traceurs de courbes permettent d’obtenir rapidement la représentation graphique d’une fonction définie par une formule algébrique, il est intéressant, notamment pour les fonctions définies par morceaux, de faire écrire aux élèves un algorithme de tracé de courbe.

Personnellement je trouve que vu la puissance des logiciels considérés, c’est un investissement en temps non rentable. J’ai donc fait le choix de montrer un exemple plutôt que de le faire créer par les élèves. Mais ce faisant la classe a progressé très vite sur cette question (d’autant plus que le graphique sera réinvesti plus tard dans le cours sur la fonction « carré » mais aussi dans un TP sur un nomogramme basé sur cette courbe).

La vision d’un point animé avec affichage de ses coordonnées et le fait de ne pas considérer le nom réel d’un point (avec réaffectation de celui-ci) ont été les atouts majeurs de ce TP.