Introduction | Le choix des grandeurs | L’intérêt de la manipulation | Les activités
Introduction
Enseignantes d’appui en réseau ECLAIR, nous intervenons régulièrement en cycle 3. Avec les collègues, nous mettons à profit ces moments de co-animation ou de dédoublement de classe pour placer les élèves en situation problème.
Seulement, dans nos réseaux, nos élèves ont de grandes difficultés : ils restent parfois bloqués devant un énoncé, cherchent l’opération qu’il « faut » poser et dans le doute, n’écrivent rien.
Bien sûr ils ne sont pas tous dans cette attitude, mais ils sont suffisamment nombreux pour que nous ayons eu envie de réfléchir à une méthode pour les faire entrer dans les problèmes.
Par ailleurs, il nous semblait que les grandeurs étaient oubliées. Non pas dans la progression mathématique de l’enseignant, mais plutôt dans le rôle qu’elles jouent pour donner du sens aux nombres et aux situations. Nous avons donc proposé cette recherche-action : travailler les grandeurs par la résolution de problèmes au cycle 3.
L’idée, pour aider les élèves à commencer une résolution, est de leur donner la possibilité de manipuler pour s’approprier la situation.
En effet, pour accéder à la conceptualisation, l’enfant doit d’abord manipuler, puis schématiser. Ces étapes de raisonnement sont incontournables. Certains enfants entrent dans la conceptualisation rapidement, d’autres ont besoin de plus de temps. Ainsi la construction du nombre ou encore l’acquisition du sens des opérations nécessitent beaucoup de manipulation, depuis la maternelle jusqu’au collège. Si on brûle les étapes (et tout dépend du rythme d’acquisition de l’enfant) les règles deviennent des recettes de cuisine, plus ou moins bien retenues.
Afin de gérer l’hétérogénéité à laquelle nous sommes tous confrontés, nous nous sommes inspirées des banques de situations de la collection ERMEL. Nous avons adapté des situations pour nos élèves pour qu’ils aient toujours la possibilité de manipuler et se construire des représentations mentales. Ainsi chaque enfant peut aller selon ses capacités vers le même objectif que les autres élèves. C’est bien là la différenciation définie par Philippe Perrenoud.
Le choix des grandeurs
1. Définition
Notre choix de placer les grandeurs au centre de notre progression a été déterminé par l’ouvrage de l’IREM de Poitiers : Enseigner les mathématiques en sixième à partir des grandeurs. Ce groupe de recherche s’est lui même appuyé sur des citations, notamment celle de Yves CHEVALLARD et de Mariana BOSCH :
L’oubli de la notion de grandeur ferme les mathématiques sur elles-mêmes. En sens inverse, l’exploration de l’univers des grandeurs constitue le point de départ de l’exploration mathématique de la diversité du monde. L’introduction mathématique au monde qui nous entoure suppose donc prise de contact et familiarisation avec l’univers des grandeurs.
À ce stade, il est légitime de s’interroger sur la définition d’une grandeur. Nous citerons ici les propos de l’IREM de Poitiers :
« Dans le vocabulaire international des termes généraux et fondamentaux de métrologie, la grandeur est définie comme l’attribut d’un corps ou d’une substance qui est susceptible d’être distingué qualitativement et déterminé quantitativement. »
Les longueurs, les aires, les volumes, les masses entrent donc dans la catégorie des grandeurs mesurables. On peut les comparer et effectuer des calculs avec de telles grandeurs.
Le temps est une grandeur repérable. Elle est associée à une échelle fixée par convention. On ne peut pas par exemple effectuer d’addition de deux temps. Pour pallier à cet inconvénient, nous parlerons donc de la durée, que nous pourrons intégrer aux grandeurs mesurables.
Restent les prix, qui ne sont pas une grandeur comme définie plus haut, car ils ne font pas intervenir une qualité de l’objet mais seulement une quantité numérique qui lui est associée. On définira ainsi les prix comme la mesure de la valeur d’un objet.
2. Un choix fondé sur la réalité du terrain
L’analyse des évaluations nationales de CM2 met en évidence la méconnaissance des grandeurs pour les élèves de notre réseau. En se penchant plus près dans ces cahiers d’évaluation, on constate que les élèves ne savent pas convertir des grandeurs dans des cas aussi simples que comparer des jours et des heures, transformer des mètres en kilomètres…
Nous expliquons cette difficulté par plusieurs facteurs :
- Les élèves rencontrent peu les grandeurs. En classe, à part le double décimètre, qui donne une image mentale du cm et du mm aux élèves de cycle 3, les enfants manipulent peu d’instruments de mesure. Et cet exemple pose déjà une limite : certes les enfants se représentent ce qu’est un centimètre, mais quasiment aucun ne se représente un décimètre. Peu de classes sont équipées d’horloge au mur… Et le constat est le même à la maison : ils « jouent » un peu avec des euros, quelques uns ont des horloges ou des montres à aiguilles, mais les grandeurs et leurs mesures s’arrêtent là en général.
- Les grandeurs rencontrées le sont souvent uniquement dans l’univers de la salle de classe : pour les longueurs ce sont cm et mm, pour les durées ce sont des heures et minutes, pour les aires ce sont des carreaux du cahier ou des cm2, pour les masses ce sont des grammes et des kilogrammes. Seuls les prix, si on les intègre dans les grandeurs, échappent à la règle et osent aller des milliers aux centièmes…
- Dans les manuels, les grandeurs sont souvent abordées artificiellement au détour d’un exercice, et nous avons rencontré peu d’ouvrages prenant le temps d’étudier les grandeurs pour elles-mêmes, de les construire. On peut citer l’exemple des exercices où l’on calcule le périmètre d’un champ rectangulaire mesurant 45 m sur 30 m, et celui-ci est représenté par un rectangle de quelques cm de long et de large… La schématisation est certes nécessaire, mais n’aide pas l’élève à se représenter cette distance.
- Les grandeurs sont souvent rencontrées à la fin de l’année, voire à la fin du cycle 3 pour les aires, les volumes , comme au collège où l’étude des solides se fait souvent à la fin de l’année. Les élèves ne les rencontrent souvent qu’une fois dans l’année… ce qui leur laisse peu de chance de s’approprier ces grandeurs.
- L’usage des tableaux de conversion : souvent l’amalgame suivant est fait : faire des conversions, c’est remplir un tableau. Si certains élèves s’y retrouvent, un très grand nombre ne sait même pas construire ce type de tableau, même au collège. Utiliser les tableaux de conversion faire perdre du sens aux grandeurs, et ne permet pas de donner de lien aux multiples et sous multiples.
- Il nous a donc paru essentiel de bâtir nos problèmes autour de la découverte de ces grandeurs, et de varier les contextes d’étude pour les manipuler sous diverses formes.
L’intérêt de la manipulation
La manipulation en mathématiques, très présente en maternelle, décroît avec le temps, pour quasiment disparaître au collège.
Les raisons évoquées sont très souvent celles du manque de temps, mais nous pensons qu’implicitement la manipulation ne fait pas très « sérieux ». Il paraît certainement plus « noble », plus « mathématique », d’avoir une belle page du cahier remplie de calculs, plutôt que d’avoir manipulé pendant une heure sans avoir forcément de trace écrite à présenter.
Pourtant les intérêts sont multiples, pour l’élève et pour l’enseignant.
Catherine Berdonneau3 dans son livre « Aider les élèves en difficulté en Mathématiques, CP/CE1 » développe les atouts de la manipulation :
1. Les intérêts pour l’élève
- Ils rentrent plus vite dans l’activité : la manipulation rompt avec les habitudes, les élèves ont l’impression de jouer. Si certains ont des difficultés pour se lancer dans un exercice en général, la manipulation peut les « débloquer » et leur donner de l’assurance,
- Ils sont libérés de contraintes qui pourraient être un frein à la compréhension : plus besoin d’écrire ni de faire des schémas propres.
- Ils peuvent recommencer autant de fois qu’ils veulent, sans avoir besoin de beaucoup de temps, contrairement à un problème « sur feuille » où si l’on veut recommencer on doit tout effacer (?) et tout réécrire, tout redessiner... Sans oublier qu’ici, l’erreur ne laisse pas de trace ! Les enfants ont donc moins de mal à tenter une approche, sans avoir peur du jugement.
- Les activités de manipulation se prêtent bien au travail en groupe, et l’on peut même le forcer en ne donnant qu’un « jeu » de manipulation par groupe.
2. Les intérêts pour le professeur
- Avoir rapidement une classe au travail et des élèves occupés, qui ne perturbent pas les autres. Il peut ainsi facilement passer voir les élèves un par un.
- Il voit en un seul coup d’oeil les élèves qui travaillent réellement, ceux qui chahutent, ceux qui n’ont pas compris et ne se lancent pas dans l’activité. Il peut ainsi rapidement réagir, contrairement à un production écrite par exemple où il y a souvent un temps de latence avant de détecter les difficultés de certains.
- Les élèves, souvent freinés par l’écriture, peuvent ici réaliser beaucoup d’exercices à la suite...
- … ou peu d’exercices, sans empêcher les autres d’avancer : chacun à son rythme réalise son travail, rendant la gestion de l’hétérogénéité possible
- Par la manipulation, les élèves qui sont plus kinesthésiques que visuels ou auditifs peuvent également être mis en confiance.
Bien sûr il existe quelques dérives possibles, comme celle où les enfants considèrent la manipulation comme un jeu, et se déconcentrent rapidement. Si les enfants ne manipulent pas souvent, c’est ce qui peut arriver. Mais si la manipulation est régulière et intégrée à la progression, les enfants perçoivent qu’elle est une part de leurs apprentissages, et se mettent sérieusement dans l’activité.
Les enfants peuvent également associer le matériel à une situation unique, et commencer leur activité sans considérer la nouvelle consigne. Par exemple avec des billets, une des activités que l’on avait proposé consistait à partager équitablement une somme, mais certains élèves n’avaient ni lu ni écouté et étaient en train de compter la somme disponible, qui était la consigne de l’activité précédente avec les billets.
Par l’expérience que nous avons eue sur le terrain, nous avons constaté que ces dérives étaient rares, et qu’en général la manipulation amenait des séances intéressantes et constructives.
Les activités
Les prix en CE2
Cette année, nous nous sommes lancées dans la confection de billets plastifiés de 10, 100 et 1000 afin de travailler la numération à travers des activités liées à des prix ou tout du moins faisant appel à la manipulation de monnaie.
Une fois achevée la confection (certes longue), nous avons pu réinvestir ces billets dans de nombreuses activités, ce qui nous fait dire que le temps passé à la confection a été largement amorti.
L’activité présentée ici utilise donc ces billets pour travailler les notions de dizaines, centaines mais en abordant la différence entre chiffre de ... et nombre de ... ainsi que la place du 0 dans l’écriture d’un nombre.
La Rançon de Lucky Luke est une activité choisie dans le ERMEL CE2, mais elle a été allégée pour nos élèves qui n’ont pas eu le temps d’aller plus loin.
Ces séances montrent bien que chez de nombreux élèves la comptine numérique est connue. Mais chez certains, cette comptine n’a pas encore de représentation assez solidement construite pour permettre de raisonner sur le sens de l’écriture d’un nombre.
1re étape : avec des petits nombres
Énoncé A :
Les Dalton ont enlevé le chien de Lucky Luke.
Lucky Luke doit leur payer une rançon en billets de 10 €.
- Averell reçoit 80 €
- Jack reçoit 120 €
- William reçoit 170 €
- Joe reçoit 230 €
Combien de billets de 10 € chacun des Dalton aura-t-il ?
Matériel :
- Les élèves disposent de billets de 10 € et de 100 €, en tas sur la table pour chaque groupe.
- Un énoncé par élève.

Les élèves travaillent par groupe de 3 ou 4.
La lecture de l’énoncé est faite par le maître, surtout pour accrocher les élèves avec les personnages, et expliquer les mots qui ne seraient pas compris (rançon).
Les élèves disposent dans un premier temps de 15 minutes de recherches. Ils écrivent leurs réponses sur les cahiers de brouillons. Ils n’ont pas le droit d’effacer s’ils se trompent, mais doivent répondre par une phrase.
Le premier énoncé est volontairement choisi avec des petits nombres pour permettre aux élèves de manipuler. Ils peuvent concrètement prendre la somme réclamée dans leurs mains. Cette étape est importante pour tous les élèves. Avec les plus rapides, elle permet de vérifier une bonne compréhension de l’énoncé.
1. La première rançon, 80 €
Les élèves les plus en difficultés ont tous pris les 80 € en comptant de 10 en 10. Puis, en passant à chaque table, j’ai pu demander aux élèves combien de billets de 10 € cela faisait. Là, ils confondaient somme demandée et nombre de billets. Je les ai questionnés, leur ai fait relire la consigne, puis ils ont fini par dire qu’il fallait 8 billets.

Ensuite nous passions à la mise en commun pour cette première rançon. Les réponses étaient assez unanimes, pour réunir 80 € il fallait 8 billets de 10 €. Un élève prenait les 8 billets et comptait de 10 en 10, la classe était d’accord.
Je précisais alors aux enfants qu’ils n’étaient pas obligés d’utiliser les billets, le problème était réussi lorsque ils avaient écrit les phrases réponses.
2. Les autres rançons
Petit à petit les élèves ont tous réussi à écrire, pour chaque somme, le nombre de billets de 10 € correspondant. Ils devaient s’y reprendre à plusieurs fois, car s’ils savaient la comptine de 10 en 10, ils oubliaient de recompter ensuite les billets un par un. Tout simplement parce qu’ils ne voyaient pas la nuance entre euros et billets (c’est-à-dire entre le nombre et son nombre de dizaines).

Puis nous repartons sur une phase de recherches pour ceux qui n’avaient pas fini ou qui veulent changer leurs réponses. D’autres, qui ont tout fini et dont j’ai corrigé les productions passent à l’énoncé suivant.
Au bout de 10 minutes, c’est de nouveau la mise en commun. Je note leurs réponses au tableau. Nous faisons apparaître la règle que si un nombre se termine par 0, on peut trouver rapidement son nombre de dizaines en « enlevant » le 0.
Énoncé B :
Joe a reçu 40 billets de 10 €. Pour que cela prenne moins de place dans son porte-monnaie, il va échanger ces billets à la banque contre des billets de 100 €.
Combien aura-t-il de billets ?
Je donne un énoncé par élève, les billets sont toujours sur les tables.
Nous procédons à la mise en commun au bout de 10 minutes : cette situation aboutit à la conclusion que le nombre de centaines d’un nombre se terminant par deux 0 s’obtient en « enlevant » les deux 0 à la fin du nombre.
Les plus rapides, eux, n’ont fait que jouer avec les billets puisqu’ils savaient déjà déterminer le nombre de dizaines. Ils ont entraîné avec eux les plus hésitants, fascinés par la rapidité avec laquelle ils trouvaient les réponses.
Pour ces plus rapides, j’ai ensuite donné des nombres plus grands et donc inaccessibles par la manipulation. Ils sont donc arrivés à un stade d’automatisation.
Ce type d’activité me permet donc de gérer l’hétérogénéité, de mettre au travail même les plus en difficulté et de faire travailler, par tutorat, les plus avancés.
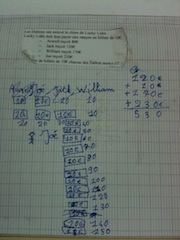
Lors de l’institutionnalisation nous avons pu dégager la procédure experte. Pour ce faire, j’ai noté leurs réponses au tableau en présentant les nombres en deux colonnes : une pour indiquer le montant de la rançon et l’autre pour indiquer le nombre de billets. J’ai rajouté en en-tête de ces colonnes les termes « nombres » et « nombres de dizaines ».
Ainsi s’est dégagé en parallèle le nombre et le nombre sans le 0. La règle a donc été dictée par les élèves.
2e étape : pour aller plus loin, des nombres plus grands
Les Daltons ont enlevé le chien de Lucky Luke. Lucky Luke doit leur payer une rançon en billets de 10 €.
- Averell reçoit 260 €
- Jack reçoit 860 €
- William reçoit 1 500 €
- Joe reçoit 2 000 €
Combien de billets de 10 € chacun des Dalton aura-t-il ?
Joe a reçu 350 billets de 10 €. Pour que ce soit moins lourd, il va échanger ces billets à la banque contre des billets de 100 €.
Combien aura-t-il de billets ?
Les longueurs en CM2
Nous avons créé des activités qui permettent d’utiliser divers instruments de mesure, et de mesurer « dans toutes les directions ».
En effet, bien souvent, l’élève ne mesure que des longueurs qui « tiennent » sur une feuille A4, avec un double ou triple décimètre positionné à l’horizontale.
Pour la 1re activité autour des longueurs, nous leur avons demandé de mesurer différents « objets », sans leur fournir ni schéma ni explication.
Ils devaient donc trouver à quoi correspondait la mesure :
- de la largeur et de la longueur d’une table d’écolier,
- du périmètre crânien du professeur,
- de la largeur et de la longueur du grand bâtiment,
- de la largeur et de la longueur de cette feuille,
- de la largeur et de la longueur du rectangle dessiné,
- de la largeur et de la longueur de la salle de classe.
Pour ce faire, ils étaient en groupes (3 ou 4 élèves) et devaient choisir parmi différents instruments (que nous possédions en double) :
- une règle graduée,
- un décamètre,
- une ficelle et une règle graduée,
- un mètre de couturière,
- un mètre de bricoleur,
- la règle du tableau.
Télécharger le document élève :
Ces enfants, âgés d’une dizaine d’années, ne découvraient pas ces instruments pour la première fois, mais ce qui les a surpris, c’était de les utiliser dans un autre contexte que l’habituel. En effet,
- le mètre de couturière leur évoquait bien des mensurations, mais plutôt celles de la taille ou de la poitrine...
- le décamètre était associé à l’athlétisme, pour le saut en longueurs ou pour la course...
- la règle du tableau était dévouée... au tableau, et à la maîtresse !
1re difficulté : le choix de l’outil
Ce choix fut assez rapide et judicieux en général. Pour cette activité, les « objets » à mesurer préfiguraient facilement l’outil à employer de par leur longueur : plus l’objet était grand, plus l’instrument de mesure choisi était long...
2e difficulté : comment positionner l’outil
En CM2, les enfants savent mesurer un segment avec leur règle graduée en positionnant le « zéro » sur une extrémité du segment. Pour le décamètre, certains étaient gênés par l’absence du zéro. Conditionnés par l’habitude que le zéro soit décalé par rapport au bord de la règle, ils s’appliquaient à laisser une petite distance comparable entre le début du décamètre et le bord du mur. Pourtant les graduations « 1 » et « 2 » étaient bien écrites sur un côté du décamètre, mais dans la partie noire et donc pas très visibles.
Sur la photo suivante nous avons repassé en orange la graduation 1.

Le placement de l’extrémité du décamètre...
Lorsque les élèves mesurent une longueur sur leur cahier, leur règle est à l’horizontale. Ici pour mesurer la longueur d’un mur, ils devaient positionner le décamètre à la verticale. Celui-ci était donc soumis à la force de pesanteur.
Mesure « horizontale » à la verticale...
Les élèves n’étaient pas gênés de laisser « pendouiller » le décamètre, mais tous ont réagi lorsqu’on leur a fait la remarque, et l’ont tendu.
Dans le même registre, pour mesurer la largeur de la salle, ils faisaient généralement leur mesure au mur, où il y avait notamment une bibliothèque collée au mur. Ils décollaient donc sans scrupule le mètre du mur, et passaient par dessus la bibliothèque, rallongeant d’autant leur mesure.
Comment contourner la difficulté...
Par contre aucun groupe n’a pensé à vérifier que les deux extrémités étaient à la même hauteur.
Certains se sont également mis dans des situations assez inédites...
De l’art de bien se placer pour mesurer une longueur avec un décamètre...
3e difficulté : Lire avec les graduations
Sur un double décimètre, nous n’avons jamais vu d’indication concernant l’unité de longueur.
Les élèves doivent savoir que l’unité en question est le centimètre ! Étonnées par ce manque, nous avons observé d’autres instruments de mesure de longueur. Il n’y a quasiment jamais les unités. Cela pousse à la réflexion lorsqu’on sait combien on peut être exigeantes envers les élèves pour que eux, sur leur copie, indiquent l’unité, alors qu’elle n’apparaît même pas sur les instruments ! Même les règles anglo-saxonnes affichant d’un côté les cm et de l’autre les pouces n’ont pas systématiquement l’unité indiquée...
Sur la règle du tableau, pas d’unité non plus. Sur un double décimètre, la « petite » graduation représente un millimètre, mais sur la règle du tableau la petite graduation représente 1 cm... Et nous nous faisons la réflexion que nous n’aidons pas les élèves quand nous faisons les dessins au tableau, en prenant une échelle 10 fois plus grande pour que le dessin soit bien visible.
Le décamètre est donc plus rigoureux, car tous les mètres la longueur est indiquée en rouge : « 1m », « 2m »… Toutefois la longueur indiquée ne correspond pas au nombre de cm depuis l’origine, mais au nombre de cm depuis le dernier mètre entier... C’est en fait une succession de mètres collés les uns à la suite des autres. Ce que les enfants n’ont pas forcément tous vu ! Certains se contentaient donc de regarder en face de quelle graduation tombait la fin du mur... Ainsi ils nous ont affirmé que la largeur du bâtiment était 89 cm !
La lecture de l’extrémité finale du décamètre nous a montré à quel point les enfants n’avaient pas de représentation mentale des longueurs, car leur décamètre étant entièrement déroulé, au lieu de lire 10 m et 15 cm, ils comptaient depuis 10m : « 11, 12, 13... 22, 23, 24, 25 m ! »
L’extrémité du décamètre
Cette erreur prouvait également qu’ils n’établissaient pas de lien entre le préfixe « déca » et 10 m. À ce propos nous conseillons, lors de mesures de ce type, de bien utiliser des décamètres simples et non pas des doubles ou triples décamètres, afin de laisser une image mentale de ce que représente un décamètre !
Notons que contrairement au décamètre, le mètre du bricoleur affiche bien la longueur depuis l’origine, et que cette longueur est écrite en cm (mais sur notre mètre l’unité n’était pas non plus renseignée !)
4e difficulté : report de l’outil
Lorsqu’on donne à mesurer une longueur sur une feuille, il est rare que celle-ci dépasse 20 cm. En réalité, surtout au collège, les dimensions des figures dépassent rarement 8 cm. Nous avons réalisé cela en voyant les élèves mesurer la longueur du bâtiment (qui était voisine de 30 m).
Plusieurs groupes ont bien reporté 3 fois le décamètre (ils devaient établir que la longueur était 10 m + 10 m + 9,89 m) mais n’ont gardé que le dernier résultat comme mesure ! Ils annonçaient que le bâtiment mesurait 9,89 m de long !
D’autres ont bien ajouté les 3 mesures, mais ne se sont pas facilité la tâche, car ils ont déroulé totalement le décamètre et ont donc gardé pour les deux premières mesures 10 m et 15 cm. Ce qui leur a ensuite posé problème pour ajouter les 3 longueurs, car ils ne savaient plus quoi ajouter à qui. Ce qui prouve que la numération de position n’est pas encore bien en place.
Un groupe qui mesurait la largeur de la salle de classe nous a tout de même interloquées, car ils utilisaient le mètre du bricoleur (de longueur 5 m) : ils avaient donc positionné l’extrémité du mètre sur le mur du fond, et prenait la mesure sur le mur. Une fois le mètre entièrement déroulé, ils ont conclu que le mur mesurait 5 m de long, puisqu’on ne pouvait pas aller plus loin !
5e difficulté : la précision du résultat
Après toutes les erreurs constatées lors de la prise de mesure, nous avons beaucoup apprécié la précision qu’ils donnaient à leur résultat. Par exemple leur décamètre pendouillait, ou bien ils reportaient l’instrument « dans le vide », mais tentait ensuite de donner un résultat au millimètre près pour la longueur du bâtiment !
Marque « dans le vide » pour le report du décamètre
Bilan de cette activité
Cette activité, très riche d’enseignement pour nous professeurs, nous a permis de faire le point sur les principales difficultés des élèves :
- Le sens de l’addition n’est pas acquis par tous. Il est encore trop limité à la réunion de collection d’objets. Ici pour mesurer le grand bâtiment, on a pu mettre en évidence qu’ils devaient reporter 3 fois le décamètre et additionner les 3 longueurs trouvées. Pour mesurer la salle de classe également, il fallait additionner 2 mesures de longueur car le mètre du bricoleur n’était pas assez long.
- Les multiples/sous multiples du mètre ont permis de redonner du sens à l’écriture décimale : nous n’avons pas sorti d’un chapeau un tableau de conversion ! Les enfants ont pu établir les conversions du millimètre au décamètre, en ayant les objets réels sous les yeux. Ils ont visualisé qu’un décamètre était 10 fois plus grand qu’un mètre, qu’un cm était 100 fois plus petit qu’un mètre... Nous avons également pu faire le lien avec la numération de position et le « poids » d’un chiffre, surtout lorsqu’on a repris l’extrémité du décamètre et comprendre ce qu’étaient les 15 graduations après la marque des 10m.
- Enfin on a mis en évidence l’importance de donner l’unité de longueur de son résultat !
La division en CM
L’algorithme de la division est souvent difficile à comprendre pour les élèves car il n’a aucun sens pour eux. Pour leur enseigner cet algorithme, nous avons voulu le raccrocher à une situation « clef » qui leur soit parlante : le partage d’un trésor. Nous nous sommes ainsi largement inspirées des activités prônées par ERMEL, ou par R. Brissiaud dans le manuel « J’apprends les Maths ».
Nous avons programmé une activité filée sur plusieurs semaines, afin de laisser aux élèves le temps de digérer cet algorithme. Nous faisions une séance « division » par semaine.
Pour cette activité, il faut une très grande quantité de billets. Le mieux est de les fabriquer en imprimant les valeurs sur des papiers de couleurs différentes, et de les plastifier pour faciliter la préhension. L’idéal pour une classe de 24 élèves est d’avoir environ 50 billets de 1 000€, 200 billets de 100€, 200 billets de 10€ et 200 pièces de 1€... Mais pour les pièces il vaut mieux acheter les petites pièces en plastique du commerce !
Séance 1 : définition des conditions du partage
Séance 2 : introduction du vocabulaire de la division euclidienne, unicité du résultat
Séance 3 : entraînement avec des divisions par 4
Séance 4 : changement de diviseur
Séance 5 : Sans les billets...
Séance 6 : vers l’algorithme de la division euclidienne posée...
(pour connaître la progression détaillée, télécharger le fichier ci-dessous)
Aires et multiplication en CM
À l’école primaire, les tables de multiplication sont souvent seulement introduites comme une addition répétée (4 × 7 c’est 7 + 7 + 7 + 7). Ainsi, lorsque les élèves arrivent au collège, très peu sont capables de dénombrer le nombre de carrés dans un rectangle de 4 carrés de large sur 7 carrés de long... La progression suivante présente les tables sous la forme de rectangles multiplicatifs, ce qui permet :
d’avoir une image mentale de ce que représente les tables de multiplication
d’avoir des cartes de tailles proportionnelles au résultat
d’illustrer la commutativité par superposition des cartes de même taille
d’illustrer le lien entre les différents résultats par superposition des cartes
de travailler la notion d’aire de rectangle
d’obtenir une technique de calcul de multiplication qui ait du sens (même pour les nombres décimaux) La progression détaillée correspond à des classes de cycle 3. Elle peut bien sûr convenir à des élèves de collège en difficulté faces à ces notions. Pour les cycle 2, la progression peut bien sûr être adaptée.
Matériel à construire au préalable : imprimer les différentes tables sur du papier de couleur (fichier « carte table » ci-dessous). Nous avons choisi les couleurs suivantes :
- table de 2 : jaune pâle
- table de 3 : rose pâle
- table de 4 : jaune fluo
- table de 5 : bleu ciel
- table de 6 : rose foncé
- table de 7 : vert pâle
- table de 8 : orange
- table de 9 : vert foncé
- table de 10 : bleu foncé
Bien sûr le choix des couleurs est libre ! L’important c’est de trouver une cohérence entre les séries de tables : 2, 4 et 8 (série « jaune »), 3 et 6 (série « rose »), 5 et 10 (série « bleue »).
L’idéal est de plastifier les cartes pour garantir leur solidité, et d’en faire un jeu aimanté pour le tableau.
Sommaire :
Séance 1 : les tables de 2, 4 et 8 (et calcul de 12 × 13)
Séance 2 : les tables de 5 et 10 (et l’utilité d’utiliser la table de 10 !)
Séance 3 : Tables de 3 et 6 (et calculs du type 23 × 46)
Séance 4 : Table de 7 (et calculs du type 127 × 76)
Séance 5 : Table de 9 (et calculs du type 2 957 × 86)
Séance 6 : Lien avec la multiplication posée
Séance 7 : Extension aux nombres décimaux
Progression détaillée et documents à télécharger :
Le dernier document à télécharger comporte les fiches récapitulatives des liens entre chaque table ainsi que la grande table de Pythagore géométrique.
Bibliographie :
« Je construis la multiplication et les tables 8/10 ans », René COULON, Sylvie HEUSSCHEN, Françoise LUCAS, Luc MORNARD, éditions De Boeck.

Commentaires